數列探索性問題分類和對應解題思路分析
黃保球
(江蘇省清江中學)
數列問題是高中數學重要的考查題型,主要包含求數列的通項、數列求和以及以數列為載體的綜合問題.近年來,數列相關的探索性問題考查頻率在逐漸提升,要求學生在掌握數列基礎知識的前提下求解相關探索性問題,具有一定的綜合性和難度.本文主要介紹三類不同的數列探索問題:條件探索性問題、結論探索性問題、存在性探索問題,并結合例題對不同類型問題的方法和思路進行分析.
1 條件探索性問題
與數列相關的條件探索性問題常常會給出確切的結論,要求考生對滿足結論的條件進行分析和探索,運用分析法解題的關鍵在于從結論著手找出必要條件.解答條件探索類數列問題,具體的解題思路如下:
1)根據問題給出的結論得到相關必要條件,結合已知條件將必要條件轉化為具體的關系式;
2)結合題意,給關系式添加限制條件,求解關系式,即可得到使結論成立的條件.
例1已知數列{an}為等差數列,a1=2,{an}的前n項和為Sn,數列{bn}為等比數列,且a1b1+a2b2+…+anbn=(n-1)2n+2+4對任意n∈N*恒成立.
(1)求數列{an},{bn}的通項公式;
(2)各項均為正整數的無窮等差數列{cn}滿足c39=a1007,且存在正整數k使c1,c39,ck成等比數列.若數列{cn}的公差為d,求d的所有可能取值之和.
分析聚焦第(2)問,首先問題給出已經成立的結論:c1,c39,ck為等比數列,由該結論可推導出必要條件.結合第(1)問的通項公式和條件c39=a1007可求出c1,c39,ck的表達式,將其代入必要條件得到具體等式.結合題意給等式添加限制條件,此時可求得充分條件d的值,進而求出d的所有可能取值之和.
解(1)an=2n,bn=2n(求解過程略).
(2)當d=0時,符合題意.
當d>0,由c39=c1+38d=2014,可得
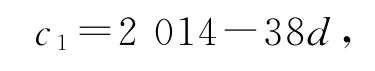
ck=c39+(k-39)d=2014+(k-39)d,將c1,ck帶入中,可得
(2014-38d)[2014+(k-39)d]=20142,化簡得kd-39d=53k-53×77,則
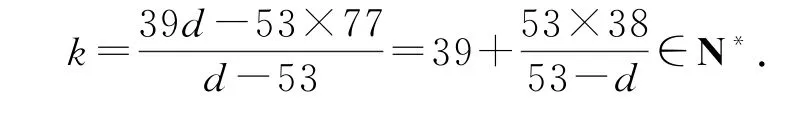
又因為c1=2014-38d=38(53-d)>0,d>0,所以d=34,51,52,故d的所有可能取值之和為137.
變式已知數列{an}是首項為a,公差為1的等差數列,若對任意n∈N*都有bn≥b8成立,則實數a的取值范圍為_________.
分析首先對結論bn≥b8進行分析,結合{an}是遞增數列且公差為1,可得與a有關的不等式組,求出的范圍即為a的取值范圍.
解因為,若對任意n∈N*都有bn≥b8,即bn-b8≥0,則,又因為{an}是遞增數列且公差為1,所以a9>0且a8<0,所以解得-8<a<-7.
綜上,實數a的取值范圍為(-8,-7).
2 結論探索性問題
與數列有關的結論探索性問題主要是根據具體的條件推導具體結論或判斷所給結論的正誤,解答這類問題可采取特例法,即從特殊情況著手分析、探索得到結論后,驗證一般情況下該結論成立與否.求解數列的結論探索性問題,解題思路通常如下:
1)對問題題意進行分析,根據已知條件對結論進行猜想;
2)通過數列求通項和前n項和的運算方法,判斷猜想的結論正確;
3)證明猜想結論.
例2已知各項均為正數的數列{an}滿足,且a2+a4=2a3+4,其 中n∈N*.
(1)求數列{an}的通項公式;
分析主要對第(2)問進行分析,要比較Tn和2的大小關系,首先憑借第(1)問{an}的通項公式,求出數列{cn}的通項公式,分析通項公式的結構特點,采取錯位相減法求解Tn的表達式為.易得到Tn<2的大小關系,故猜想結論Tn<2,證明過程即對應整個推理過程.
解(1)an=2n(求解過程略).
(2)結論為Tn<2,證明過程如下.

3 存在性探索問題
存在性探索問題是指在已知條件下對與數列有關的某一參數或某一結論成立存在的可能性進行探索,通常運用反證法進行解答,即假設問題給出的結論成立,在該前提下進行邏輯推理,若推斷過程中存在矛盾,則假設不成立,反之則可得到存在的對應具體值.解答數列的存在性探索問題,常見的解題思路如下:
1)假設問題中需要探索的存在性條件或結論成立,得到對應的關系等式;
2)結合已知條件,對推導得到的關系等式進行驗證;
3)若驗證過程中存在矛盾,對應的假設不成立,該條件或結論不存在;反之,若無矛盾之處,則假設成立.
例3設數列{an}的前n項和為Sn,且Sn=n2,數列{bn}滿足),是否存在m使得數列{bn}中某項bt滿足b1,b4,bt(t∈N*,t≥5)成為等差數列? 若存在,寫出符合題意的m的個數;若不存在,說明理由.
分析問題對參數m的存在性進行探索,解題時要先求出an,bn的通項公式,假設存在m使得數列{bn}中b1,b4,bt(t∈N*,t≥5)成等差數列這一結論成立,則2b4=b1+bt,根據已知條件求出b1,b4,bt的具體表達式,并代入2b4=b1+bt中,判斷等式是否成立.若成立,則可求得參數m的具體個數,此時應結合m∈N,t∈N*,t≥5進行判斷,求出符合結論的m的個數.
解因為Sn=n2,Sn-1=(n-1)2,所以當n≥2時,有an=Sn-Sn-1=2n-1.
又因為當n=1時,a1=S1=1符合an=2n-1,即{an}的通項公式為an=2n-1,所以
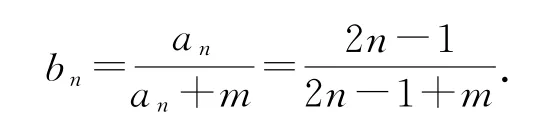
由題意得2b4=b1+bt,則

綜上,當m=6,7,8,9,11,14,17,23,41時,存在t=43,25,19,16,13,11,10,9,8 滿足題意,即存在m∈N 使得b1,b4,bt(t∈N*,t≥5)成等差數列,滿足題意的m有9個.
數列探索性問題的考查具有一定的意義,不僅要求學生熟練掌握并運用數列求通項以及數列求和方法,還要求學生具有一定的邏輯思維和創新能力.分析上述三類數列探索性問題不難發現,不同類型問題對應不同的解題策略和思路,學生應熟悉和掌握這些內容,才能靈活運用不同方法解題.
(完)

