泊松克里金算法在核輻射場重構中的應用研究

王振宇，黃偉奇,*，孫 健，彭廣宇

(1.陸軍防化學院，北京 102205；2.湖南交通職業技術學院，湖南 長沙 410132)

掌握輻射劑量場的分布對實施輻射防護行動具有重要意義，掌握輻射劑量場分布的方法主要可分為計算和監測兩大類：計算類有點核積分、蒙特卡羅、離散縱標等方法；監測一般指部署固定或移動輻射測量設備來獲取輻射場數據。當放射源的活度、位置等信息未知時，輻射劑量場分布的調查主要依靠輻射探測器監測，監測方法的缺點是監測數據分布離散、成本高。而插值算法能在少量監測數據的基礎上，通過構建數學模型對未知輻射劑量場分布進行重構，研究插值算法有助于快速、低成本地解決輻射劑量場分布問題。

插值算法是一種常見的數據處理方法，在各領域均有不同程度的應用。在進行輻射監測時，合理運用插值算法可提高計算效率。Ródenas等[1]和Wang等[2-3]分別采用線性插值和網函數插值完成了監測數據呈網格均勻分布時的輻射劑量場的插值重建。但實際上監測數據呈離散分布的情況更普遍，此時相對復雜的反距離權重法[4-6]、克里金(Kriging)法[7]和徑向基函數法[8-9]能進行輻射劑量場的插值重建。此外還有一些考慮到輻射場特性的改進插值方法，如張敏[10]在反距離平方加權法的基礎上提出的輻射劑量值占優構造還原法。

泊松克里金法屬于改進的插值算法，最早由Monestiez等[11]在調查長須鯨數量分布時提出，Zhao等[12]將其應用于輻射場的插值重構。實際上，泊松克里金法并沒有改變克里金法的求解方法，全局插值優化時仍存在最優解無法收斂的問題，此外泊松克里金法在輻射監測領域的應用較少，參數影響效果、使用范圍與效果有待進一步研究討論。本文嘗試在泊松克里金優化計算中采用代理模型的方法，通過實驗分析參數影響的效果，并用不同條件下的輻射場進行驗證，為相關研究提供參考。

1 泊松克里金算法

1.1 泊松克里金算法原理

(1)

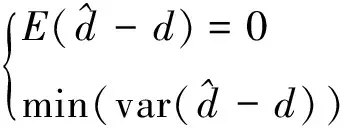
(2)

泊松克里金算法是克里金插值算法的一種特殊應用，主要區別是泊松克里金算法用觀測數據取代真實數據進行無偏估計。泊松克里金算法主要應用于真實樣本數據難以獲取的情況，其假設是觀測值與真實值之間符合泊松分布的關系。在輻射場測量中，由于放射性衰變規律和輻射探測器原理的限制，真實的劑量率無法測得，只能獲得其觀測值x。根據輻射場計數泊松分布理論，輻射探測器獲得的劑量率觀測值也服從泊松分布關系[12]，即：

x|d～Poisson(d)

(3)

故本文采用泊松克里金算法，即用樣本的劑量率觀測值xi對輻射場真實劑量率進行無偏估計，估計值的表達式示于式(4)。

(4)

求解出滿足條件的一組最優權重系數ci，即可求得輻射場真實劑量率的估計值。

1.2 基于代理模型的泊松克里金算法求解

克里金插值算法的權重系數方程組的求解通常采用拉格朗日乘數法，該方法只能得到局部最優解。前期計算中發現，當輻射場劑量率數據多時，會出現計算時間長、最優解無法收斂的情況。本文將克里金代理模型用于泊松克里金算法的求解。代理模型是指可替代復雜真實模型的一類簡化近似數學模型，克里金代理模型是代理模型的一種。本文在泊松克里金理論的基礎上對克里金代理模型進行適當修改，同時將模式搜索算法用于最優解的收斂優化。

在構建的泊松克里金代理模型中，某點的輻射場真實劑量率d可表示為回歸模型mTβ與隨機誤差e的和[13-14]：

d=mTβ+e

(5)

式中：mT為回歸模型基函數，為行向量；β為回歸系數，為列向量；e為誤差函數。同時在泊松克里金算法中，輻射場劑量率觀測值x服從期望為真實值d的泊松分布，根據全期望公式E(x)=E[E(x│d)]與總方差公式var(x)=E[var(x│d)]+var[E(x│d)]，可求得劑量率觀測值x的期望與方差：E(x)=mTβ、var(x)=mTβ+e。因此劑量率觀測值x也可表示為回歸模型與整體誤差之和(式(6))，其中的mTβ和e的取值與式(5)不同。

x=mTβ+e

(6)

因此，在泊松克里金代理模型中，真實值的估計值可用矩陣表示為式(7)。

(7)

式中：回歸模型的基函數mT和誤差函數e為可選擇的已知參數，基函數mT為可變化階次的多項式函數，后續計算中用矩陣M表示一組基函數mT；誤差函數e之間的相關性用相關系數表示，其中矩陣R表示樣本數據的相關系數；向量cT為權重系數。回歸系數向量β與權重系數向量cT為未知參數，需單獨求解。

回歸系數β：為確定最優參數β，可根據樣本點輻射劑量率觀測值X進行最大似然估計(X為x的矩陣形式)。在模型中，輻射場劑量率是一個n維二元高斯分布問題，樣本觀測劑量的似然函數可構建為式(8)。

(8)

式中：L為似然函數；σ2為高斯分布的方差；n為坐標向量的維度(本文取n=2)，求解式(8)后可得：

(9)

(10)

將式(9)、(10)代入似然函數(式(8))中，忽略常數項后可將似然函數化簡為：

(11)

在最大似然估計中，似然函數(式(11))為目標函數，相關系數矩陣的行列式|R|為自變量。通過模式搜尋算法，可逐步逼近最優相關系數矩陣R，進而也可求出回歸系數β。通過相關系數矩陣R也能確定相關系數模型的具體參數，利用該相關系數模型可求解待估計點的相關系數rT。

(12)

同樣通過拉格朗日乘數法求解后，輻射場真實劑量率的估計值表達式為：

(MTR-1M)-1MTR-1X

(13)

(14)

2 泊松克里金法參數影響分析

為研究泊松克里金算法中參數的影響，基于SuperMC軟件構建一個室內多放射源虛擬輻射場。該虛擬輻射場尺寸為40 m(長)×30 m(寬)，含兩個活度為3.7×108Bq 的137Cs和活度為1.85×108Bq的60Co放射源。通過計算得到距地面1 m高度處的當量劑量率，如圖1所示。采用datasample函數從圖1中隨機均勻抽取100個數據作為樣本數據。該樣本數據用于分析泊松克里金代理模型中各參數變量對輻射場插值還原結果的影響。

2.1 多項式基函數的影響

多項式基函數的階次影響回歸模型擬合的整體趨勢，擬合結果通過判定系數(R2)來評價，R2是線性回歸中對估計的回歸方程擬合優度的度量，其計算公式如式(15)所示。不同階次多項式的擬合結果列于表1。

(15)

式中：SSE為殘差平方和；SST為總離差平方和。

表1 回歸模型擬合結果Table 1 Regression model fitting result

由表1可知，多項式階次越高，判定系數R2越大，即擬合效果越好，但系數個數增加，計算更加復雜。其中二次多項式擬合與三次多項式擬合結果中R2相差較小，系數個數卻相差較大。綜合上述因素，選擇二次多項式為回歸模型的基函數。

2.2 誤差相關模型的影響

不同點位處的誤差具有相關性，這也是不同位置輻射劑量率的相互關聯在數學模型上的具體體現。常用的相關模型列于表2。

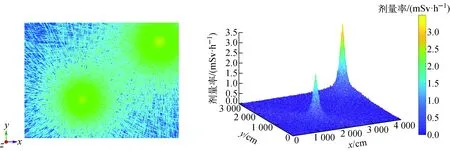
圖1 距地面1 m高度處的當量劑量率Fig.1 Equivalent dose rate at height of 1 m above ground

表2 相關模型函數Table 2 Correlation model function

圖2 各相關系數模型函數曲線Fig.2 Correlation coefficient model function curve

由圖2可看出，總體上相關系數R隨距離d的增大而減小，參數θ主要影響距離d與相關系數R之間的函數關系。當θ<0.1時，無論距離d大小，相關系數始終接近于1；當θ增加時，呈現距離近處的相關系數大，距離遠處的相關系數小，當θ增加至一定值時，相關系數隨距離的增大迅速減小，且距離稍遠處的相關系數為0，此時繼續增加θ對模型函數的影響較小。如在EXP、LIN、SPHERICAL、CUBIC、SPLINE模型中，θ=20的函數曲線與θ=50的函數曲線十分接近，GAUSS模型中θ=50的函數曲線與θ=100的函數曲線接近。因此在后續泊松克里金代理模型的最優相關系數求解中，可將模式搜索算法中θ的取值限定在一定范圍內，在EXP、LIN、SPHERICAL、CUBIC、SPLINE模型中θ∈(0.1,20)，GAUSS模型中θ∈(0.1,50)。在此基礎上，采用不同的相關系數模型對原輻射場進行插值還原。主要參數如下：采用二階多項式回歸，GAUSS模型θ∈(0.1,50)，初始θ=25，其余模型θ∈(0.1,20)，初始θ=10。各模型插值還原的效果示于圖3，圖中黑點為樣本數據。

圖3 不同相關模型對輻射場插值還原效果Fig.3 Radiation field reconstruction effect of different related models

在CUBIC和SPLINE兩種模型結果中，相關系數隨距離的增加迅速減小，與其他模型相比，在同一距離處有更小的相關系數，因此同一峰上的不同數據被識別成多個單峰。EXP、LIN和SPHERICAL三種模型形成的數據不夠平滑，不符合實際輻射場連續場的特征，其中EXP模型形成的輻射峰值底部較大，不符合輻射峰較尖銳的特征，會錯誤地增加輻射場區域面積。而GAUSS模型形成的峰與原始數據較一致，且平滑效果較好。此外，對比樣本數據點可發現，GAUSS模型還原的輻射場最高劑量率為2.5 mSv/h，明顯高于樣本數據2 mSv/h，且與原始數據趨勢一致。在實際應用中，這種尋找樣本數據范圍外的熱點區域的功能十分重要。綜上所述，GAUSS相關系數模型較適用于γ射線在空氣中形成的輻射場插值還原。

3 實驗驗證

3.1 真實輻射場的構建與測量

實驗場地選在室內，場地尺寸為15 m×20 m×4 m。以1 m為間隔在實驗場地面上建立x-y坐標系，用標記貼在網格點處順次編號標記。本實驗共設2組，放射源均為137Cs。單源組放射源活度為1.746 MBq；雙源組中一號放射源活度為0.786 MBq，二號放射源活度為0.96 MBq。

采用6150AD-b閃爍體探測器(卡迪諾科技貿易有限公司，國防科技工業電離輻射一級計量站于2013年12月26日校準)進行測量，探測器能量響應范圍為23 keV～7 MeV，最大誤差為±30%。實驗測量高度為0.5 m，與放射源之間的測量角度保持在±80°以內，測量過程中保證儀器與放射源間無障礙物。

經過對原始數據進行判棄篩選，取某點處連續3次所讀取數據的平均值作為該點的最終測量劑量率。經過數據處理，單源輻射場、雙源輻射場的三維分布和等高線圖分別示于圖4、5，其中單源輻射場最高劑量率為5.7 μSv/h，雙源輻射場2號峰劑量率為2.8 μSv/h、3號峰劑量率為3.3 μSv/h。

圖4 單源輻射場分布Fig.4 Radiation field of single source

圖5 雙源輻射場分布Fig.5 Radiation field of dual sources

3.2 基于小范圍測量數據的算法驗證

小范圍輻射場數據取自上述實驗測量數據。為研究樣本點數量對輻射場的還原效果，在樣本數據量N=20、40、60、80、100、150、200、300時，進行插值計算并繪制等劑量率線圖。單源輻射場等劑量率線圖示于圖6，雙源輻射場等劑量率線圖示于圖7。

平均誤差E用于定量對比效果的影響，所有網格點位處誤差e的平均值為平均誤差E，誤差e計算公式如式(16)所示。為消除樣本數據隨機選取過程對誤差帶來的影響，對每種情況選取100個樣本數據，并進行計算分析，結果示于圖8。

(16)

圖6 單源輻射場等劑量率線圖Fig.6 Contour map of single source radiation field

圖7 雙源輻射場等劑量率線圖Fig.7 Contour map of dual sources radiation field

由圖6、7可知，隨著樣本點數量的增加，輻射場劑量率熱點區域逐漸收斂，同時輻射劑量率峰也逐漸尖銳。圖8中，當樣本點數量為10時，單源和雙源輻射場的平均誤差分別為27.63%和26.30%；當樣本點數量增加到150時，平均誤差下降較快，分別降至4.53%和4.24%；樣本點數量為150～300時，平均誤差下降較慢，最終仍分別存在2.56%和2.46%的平均相對誤差。綜上，在10%的相對誤差允許范圍內，泊松克里金算法還原輻射場的最小樣本量為網格點數的1/10。

3.3 基于大范圍(福島周邊)數據的算法驗證

為驗證該算法在大范圍輻射場的插值重構效果，從日本原子能研究開發機構(JAEA)網站獲取了福島第一核電站80 km范圍內空間劑量率的監測結果[15]，監測時間為2016年8—10月，如圖9a所示。在插值重構中分別以監測數據坐標經緯度范圍(東經140.125 3°～141.037 9°、北緯36.710 6°～38.165 3°)為x、y坐標范圍，對該區域重新劃分成200×300的網格。然后通過隨機函數選取600個劑量率數據點作為樣本數據。采用算法插值重構的輻射場分布如圖9b所示。

由圖9可知，采用算法插值重構的劑量率分布(圖9b)中峰值的分布走向與原始劑量率分布(圖9a)一致，說明在大范圍輻射場應用中，輻射場熱點區域能基本識別出來。計算顯示，其平均相對誤差為141.69%，表明熱點定位效果不如小范圍輻射場準確。此外，在大范圍輻射場計算中，形成可靠的輻射場劑量分布所需的樣本點數量較多，分析其主要原因是福島周邊大范圍輻射場中放射源的位置分布不規則，放射性核素濃度分布不均勻，形成的真實輻射場較復雜。

圖8 平均誤差與樣本點數量的關系Fig.8 Influence of sample data size on error

圖9 原始劑量率分布(a)[14]和采用算法插值重構的劑量率分布(b)Fig.9 Original dose rate distribution (a)[14] and dose rate distribution reconstructed by algorithm (b)

4 結論

本文對代理模型求解的泊松克里金算法進行了參數分析，并通過實測輻射場數據、福島核電站周邊輻射場數據進行了算法應用驗證。結果表明，該算法在小范圍簡單輻射場重構中效果較好，由30個監測點數據構建的輻射場的相對誤差在10%左右；在大范圍復雜輻射場重構中效果略差，由600個監測點數據構建的輻射場的相對誤差為141.69%。本文計算結果初步驗證了泊松克里金算法在不同條件下輻射劑量場重構應用中的可行性，證明該方法在快速、低成本解決未知放射源輻射場的重構方面中具有一定的潛力和研究價值。