基于多元線性回歸分析的高校在校大學生人數預測模型構建

秦秋生

廣西農業職業技術大學 廣西南寧 530007

1 多元線性回歸分析及其基本原理

1.1 多元線性回歸分析

為尋求一個近似數學表達式來描述若干個變量之間的相關關系，應用數理統計方法所進行的統計方法稱為回歸分析法，所求出的數學表達式通常稱為回歸方程模型。回歸分析是確定兩個或兩個以上變量因素間相互依賴的定量關系的一種統計方法，在回歸分析研究中，如果一個變量(我們稱之為因變量或被解釋變量)與其他若干個變量(我們稱之為自變量或解釋變量)之間存在線性相關關系，把這類線性回歸分析稱為多元線性回歸分析。多元線性回歸分析的主要思路是：對于給定的實際問題，找出某一個因素及對其有顯著影響的其他若干幾個因素，并通過從一組已知觀測值出發，運用相關理論及統計軟件對其進行方差分析后建立一個數學模型表達關系方式，進而對該模型的顯著性、可信度和擬合優度及標準誤差等進行統計檢驗。若檢驗通過，說明所建立的回歸模型合理可靠，回歸方程顯著性好、擬合優度強，最后，用該回歸模型對所給問題進行預測與控制，從而為做出某些決策提供參考和借鑒。

1.2 多元線性回歸模型的一般形式

假設隨機變量y與一般變量x1，x2，x3，…，xk的線性回歸模型如下:

y=β0+β1x1+β2x2+β3x3+…+βkxk+ε

(1)

其中，未知參數為β0，β1，…，βk(共k+1個)，線性回歸常數為β0，線性回歸系數是β1，…，βk；將y稱為被解釋變量(也叫因變量)，而x1，x2，x3，…，xk是k個可以精確測量并可控制的一般變量，稱為解釋變量(即自變量)。k≥2時，稱上式(1)為多元線性回歸分析模型，ε是隨機變量。

1.3 多元線性回歸分析的模型檢驗

1.3.1 檢驗回歸模型的擬合優度

對以上假設的多元線性回歸模型，我們可以利用可決系數R2去度量樣本回歸線對樣本觀測值的擬合優度：

樣本可決系數R2的取值為0≤R2≤1，R2的數值與1越接近，則回歸方程的擬合優度越高，回歸線性擬合的效果會越好；反之，如果R2的數值與0越接近，那么回歸線性擬合的效果會越差。

1.3.2 統計量F檢驗回歸方程的顯著性

即要檢驗模型的自變量x1，x2，x3，…，xk從整體上對隨機變量y是否有顯著影響。提出假設：

H0：β1=β2=…=βk=0，H1：β1，β2，…，βk不全為零，為建立對H0進行檢驗的F統計量，利用總離差平方和的分解式即SST=SSR+SSE，構造F檢驗統計量如下：

在正態假設之下，當原假設H0：β1=β2=…=βk=0成立時，F服從F(k，n-k-1)分布。因此，可以利用F統計量對回歸方程的總體進行顯著性檢驗。給定顯著性水平α，查F分布表，得到臨界值Fα(k，n-k-1)。如果F>Fα(k，n-k-1)，那么，假設H0被拒絕，此時表明回歸效果顯著；如果F≤Fα(k，n-k-1)，那么，H0被接受，此時回歸效果不顯著。

此外，也可以根據輸出的檢驗P值來判定回歸方程的顯著性：若p<α，則拒絕原假設H0從而采用假設H1，可見P值越小，即F統計量越大，則回歸方程越顯著。

2 利用多元線性回歸分析模型對高校在校大學生人數預測

2.1 對影響普通高等學校在校大學生人數的因素的分析

為了構建普通高等學校在校大學生人數的預測模型，首先應分析在校大學生的人數所受的影響因素主要有哪些方面。一般而言，有條件接受高等教育的人數受政府對當地教育實施的政策、教育經費、當地的生產總值及人們生活水平、人們的觀念、人們可支配收入、人均地區生產總值、招生人數、高校數量等因素的影響。本文主要先對定量因素進行分析，主要考慮當地每年的招生人數、人均地區生產總值GDP、高校的數量這三個影響較為顯著的因素。由當地統計局網站中的統計年鑒，可得到2010—2020年間當地每年的高校在校大學生人數、招生人數、高校的數量、人均GDP的數據(見表1)。

表1 在校大學生人數的影響因素

2.2 在校大學生人數預測模型的建立

2.2.1 判別y與x1，x2，x3相關關系

為了大致分析y與x1，x2，x3的關系，首先，利用表1的數據分別作出y對x1，y對x2，y對x3的散點圖，同時得出相應的相關系數值。

圖1 y對x1的散點圖

圖2 y對x2的散點圖

圖3 y對x3的散點圖

由上述圖1～圖3可知，y與x1，x2，x3都具有線性分布趨勢，顯示可決系數R2分別是0.984、0.942、0.934，相關系數分別為0.9920、0.9706、0.9664，均與1非常接近，可見，在校大學生人數y與這些因素x1、x2、x3的線性關系都很強，它們的趨勢圖形都是用線性模型擬合。因此可以考慮建立多元線性回歸模型，進行多元線性回歸分析。

2.2.2 在校大學生人數預測模型的建立

結合以上分析，可以初步建立如下最初的多元線性回歸模型：

(2)

其中，β0、β1、β2、β3是待估計的參數。

運用Excel做多元回歸分析，得到以下回歸模型的統計結果與方差分析結果(詳見表2和表3)：

表2 回歸模型的統計結果

表3 回歸模型的方差分析結果

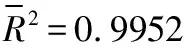
(3)

2.2.3 多元線性回歸預測模型的檢驗

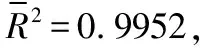
(2)回歸方程顯著性的F檢驗：查表α=0.05的臨界值Fα(k，n-k-1)=F0.05(3，7)=4.35，F的值691.5825，遠大于臨界值4.35，檢驗P值為p=5.1262E-09<0.05，即檢驗P值小于顯著水平α=0.05，可見，模型自變量x1、x2、x3從整體上對因變量y有顯著性影響，可認為自變量與因變量有較強的線性關系。所以，可以認為線性回歸效果好，回歸方程整體是顯著的。以上兩種統計方法判斷檢驗結果均合理、一致，則可說明回歸模型是較科學合理，也更為準確。

2.2.4 利用模型對高校在校大學生人數的預測

根據最終多元線性回歸預測模型(3)，我們可以對以上某地區2010年至2020年的在校大學生人數進行預測同時，把模型預測值與實際觀測值進行比較，可求出兩者的絕對誤差與相對誤差(下表4)。

表4

從以上表格可以看出，實際觀測值與模型預測值的絕對誤差與相對誤差都非常小，說明預測值與實際觀測值很接近。而且，可以計算出2010—2020年這11年間平均相對誤差僅為0.0099，即0.99%，準確程度高達99.01%，因此采用該線性回歸模型預測高校在校大學生人數是合理可靠的。

結語

本文通過對多元線性回歸分析的研究建立了某地區高校在校大學生人數預測模型，并對模型進行了有效的檢驗和預測，相對誤差極小，準確程度較高，模型合理可用。若已知當地區2021—2025年每年的招生人數、人均地區GDP及高校數量，即可以利用以上預測模型預測該地區在“十四五”規劃期間高校在校大學生人數規模，進而給當地政府在“十四五”規劃期間制定高等教育招生、就業及高等教育質量和人才培養工作方面的政策提供借鑒和參考依據。