一種基于動態逆-滑模的變形飛行器姿態控制方法研究
郭嘉寶 趙長見 宋志國
中國運載火箭技術研究院,北京 100076
0 引 言
變形飛行器是一種全新概念的多用途多形態飛行器,能夠根據飛行環境、飛行剖面和作戰任務等的需要進行適應變形,以發揮飛行器最優的飛行性能。近年來隨著各種先進技術的發展,如智能材料、傳感器、機電系統、氣動和控制等技術的進步,以及人們對飛行器靈活性、機動性、多功能和高效能等需求的不斷提高,變形飛行器已成為現代高性能飛行器的未來發展方向之一,具有極大的研究價值和應用潛力。
與現有的固定式布局飛行器相比,變形飛行器最突出的特點是其變形能力。飛行器的變形會帶來展長、翼面積、后掠角、展弦比、質心位置和轉動慣量等結構參數的變化,還會引起飛行器氣動特性和動態特性的非線性變化[1-3],這些都對飛行器的姿態穩定控制提出了挑戰。針對變形飛行器當前面臨的困難,世界上已有多個國家開展了相關領域的研究計劃[4-6],不少高校和科研機構也進行了原型設計和變形機理的研究[7-9]。
滑模變結構方法是一種對不確定參數、擾動具有很強魯棒性的控制方法,非常適合解決變形飛行器姿態控制這樣的強非線性控制問題。文獻[10]建立了一種伸縮折疊翼飛行器的LPV模型,并采用自適應滑模控制的方法保證了系統變形過程的穩定性。文獻[11]針對一種伸縮翼飛行器,利用輸入輸出反饋使飛行器的模型精確線性化,并且對于飛行器小翼伸出、收回兩個模態設計模糊滑模控制器來保證模態切換的穩定性和平滑性。文獻[12]建立了變后掠飛行器的LPV模型,通過線性分數表示法(LFR)得到了等效的線性時變系統,并引入自適應積分滑模控制補償系統的不確定因素和干擾。這些方法都保證了飛行器在變形過程中的穩定性,取得了良好的控制效果。但是以上方法只針對系統的不確定性和外界干擾設計控制器,沒有考慮變形飛行器本身的控制非仿射特性。并且變形飛行器的氣動特性較為復雜,也為LPV系統建模帶來困難,不利于控制方法的應用。
本文針對一類折疊翼飛行器的控制問題,針對飛行器的控制非仿射特性設計了動態逆控制器,將系統轉變為類似仿射的形式。然后基于滑模控制理論設計了滑模控制器來實現對擾動的補償,并采用動態滑模方法加快收斂速度,抑制抖振。最后,采用數值仿真的方法檢驗了控制的有效性。
1 變形飛行器模型
1.1 非線性動力學模型
某高速變形飛行器由內部的主體部分和外部的可變機翼部分構成,該變形飛行器的結構圖如圖1所示。可變機翼部分的外支架繞頭部2個支點定軸旋轉,從而帶動機翼可動桁架結構運動以展開或收攏,從而實現機翼面積和展長的改變。該變形飛行器的兩側機翼對稱展開或收攏,定義本文研究的高速變形飛行器的變形量為旋轉角ξ,ξ的變化范圍為0°~30°。

圖1 變形飛行器示意圖
采用多剛體方法中的牛頓歐拉法對飛行器進行動力學建模,得到該變形飛行器的六自由度非線性動力學模型。為了簡化計算方程,假設水平無側滑,即滾轉角φ和側滑角β滿足φ=β=0和角速度p=r=0,將動力學方程進行解耦,得到變形飛行器的縱向非線性動力學模型,以研究變形過程中飛行器的縱向運動。變形飛行器縱向運動方程為
(1)

1.2 氣動數據的處理
由于氣動專業給出的氣動參數是離散的點,為了建立氣動參數和旋轉角度之間的關系,下面對氣動數據進行擬合處理,擬合結果如下所示:
(2)
式中,δe代表飛行器的俯仰舵偏角;ξ為變形翼的旋轉角度,單位均為弧度。
2 控制器設計
2.1 動態逆控制器設計
根據氣動數據擬合結果可知,舵偏角δe與俯仰力矩系數是多階非線性的,所以變形飛行器姿態動力學模型是控制非仿射的,即無法把控制量U寫成b·δe。為了求解出對應的舵偏角指令,采用動態逆控制的方法將系統轉變為仿射非線性模型。
角指令為θr,角速度指令為qr,對跟蹤誤差作如下坐標變換:

(3)
則姿態角回路可以寫成如下二階不確定系統:
(4)

利用Taylor定理將f(x,u)在u=u0(x)進行級數展開得:
f(x,u)=f0(x)+g(x)u0+Δ(x,u)
(5)
式中:
(6)
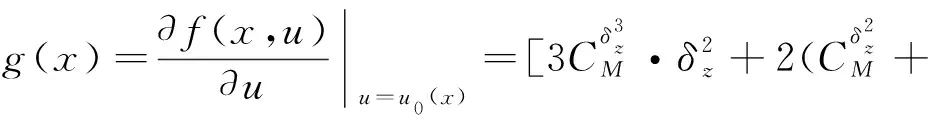
(7)

略去高階項,可以得到u0的表達式:
u0=g-1(x)[f(x)-f0(x)]
(8)
2.2 動態滑模控制器設計
下面采用動態滑模控制的方法對變形飛行器的模型誤差進行補償。取線性滑模面:
s(t)=cx1+x2
(9)
接著構造非奇異終端的動態滑模面:
(10)
式中,設計參數c>0,β>0,ε,γ均為正奇數且滿足1<ε/γ<2。
設滑模控制的控制律為v,基于時標分離原理,將系統按照被控量對控制輸入量的響應速度分成幾個子系統,并假設系統的實際控制量只作用在俯仰角速度回路上,則系統的跟蹤誤差可以表示為:

(11)
根據指數趨近律,得到非奇異終端滑模控制律如下:
(cl1+l2+η)sgn(E(t))-kE(t)
(12)
式中,k,η均為設計參數且k,η>0。
下面證明其穩定性:

(13)
(14)
根據式(9)可得:
(15)
將式(13)和(10)代入式(15)可得:
(16)
將非奇異終端滑模控制律代入上式可得:

(η+l1+l2)sgn(E(t)}
(17)
式中,E(t)sgn(E(t))=|E(t)|,所以上式變為:
η|E(t)|+cl1|E(t)|-cd(t)E(t)+
(18)

[kE2(t)+η|E(t)|+cl1|E(t)|-
(19)
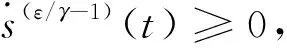
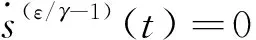

(20)


3 仿真校驗
將上文設計的動態滑模控制器和動態逆控制器引入變形飛行器非線性動力學模型中,并對變形飛行器的姿態回路進行仿真研究,以驗證所設計的姿態控制器的性能。初始仿真條件為:Ma=7,H=15km,俯仰角指令為每一時刻下的配平俯仰角。
根據俯仰角跟蹤曲線和俯仰角速度跟蹤曲線可得,本文設計的控制器能夠使變形飛行器的飛行姿態在變形過程中在較短的時間內到達期望值,無穩態誤差,能夠較好地實現姿態指令的跟蹤。

圖2 旋轉角指令和俯仰角指令

圖3 俯仰角跟蹤誤差曲線

圖4 系統響應曲線
4 結 論
針對具有強非線性、不確定性的高速變形飛行器,設計了一種基于動態逆—非奇異終端滑模姿態控制器。首先采用多剛體建模方法建立變形飛行器的縱向非線性動力學模型,并通過擬合工具得到了氣動參數隨旋轉角變化的擬合函數,得到變形飛行器縱向非仿射非線性方程。之后針對性地進行了動態逆控制器設計,將該模型轉化為仿射型非線性模型。由于模型的誤差會降低動態逆姿態控制精度,本文采用非奇異終端滑模控制對模型誤差進行校正。最后,在變形飛行器變形過程中對本文設計的控制器進行仿真驗證。仿真結果表明,本文所設計的動態逆—滑模控制器對俯仰角指令具有比較良好的跟蹤性能。

