一種級間無動(dòng)力飛行時(shí)間在線自適應(yīng)確定方法

王 智 王 鵬 何 磊

北京宇航系統(tǒng)工程研究所,北京 100076

0 引言

對于直接入軌的固體運(yùn)載火箭，為滿足入軌點(diǎn)參數(shù)及控制精度要求，可采用動(dòng)力飛行/級間無動(dòng)力滑行/動(dòng)力飛行的軌跡形式。在動(dòng)力飛行段之間增加級間無動(dòng)力滑行段，利用重力轉(zhuǎn)彎減小對動(dòng)力飛行段的攻角需求，進(jìn)而改善火箭飛行力熱環(huán)境，減小入軌點(diǎn)速度損失。

級間無動(dòng)力滑行段的飛行時(shí)間是影響動(dòng)力飛行段攻角指令大小和入軌點(diǎn)參數(shù)及控制精度的重要因素。傳統(tǒng)級間無動(dòng)力滑行時(shí)間根據(jù)入軌點(diǎn)參數(shù)要求離線確定，飛行時(shí)滑行結(jié)束條件為固定判據(jù)，無法根據(jù)實(shí)際飛行情況進(jìn)行調(diào)節(jié)，對干擾的適應(yīng)性較差。文獻(xiàn)[1-3]建立了滿足速度矢量和位置矢量約束的制導(dǎo)方法，由于未考慮飛行過程約束以及氣動(dòng)力等因素，上述制導(dǎo)方法在固體運(yùn)載火箭上升段全段飛行應(yīng)用中受到一定限制。本文針對固體運(yùn)載火箭動(dòng)力飛行/級間無動(dòng)力滑行/動(dòng)力飛行的模式，根據(jù)火箭當(dāng)前實(shí)際飛行情況、飛行過程約束以及入軌點(diǎn)約束，在線確定級間無動(dòng)力滑行結(jié)束條件，在滿足入軌點(diǎn)參數(shù)及控制精度要求的情況下，減小飛行攻角和飛行軌跡散布。

1 數(shù)值預(yù)測制導(dǎo)模型

由于固體運(yùn)載火箭的動(dòng)力學(xué)模型涉及推力、引力以及氣動(dòng)力等非線性函數(shù)，無法直接獲取精確的解析解，需要通過數(shù)值積分的方式求解微分方程組。因此，采用基于數(shù)值預(yù)測的級間無動(dòng)力滑行時(shí)間在線確定方法是實(shí)現(xiàn)固體運(yùn)載火箭上升段高精度制導(dǎo)的一種有效途徑。

對固體運(yùn)載火箭級間無動(dòng)力滑行時(shí)間在線確定方法進(jìn)行研究時(shí)，采用瞬時(shí)平衡假設(shè)：即認(rèn)為火箭無慣性地轉(zhuǎn)動(dòng)且控制系統(tǒng)理想工作。

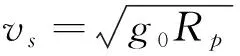
發(fā)射坐標(biāo)系內(nèi)無量綱化動(dòng)力學(xué)方程可表示為：

(1)

式中，x，y和z為火箭在發(fā)射坐標(biāo)系內(nèi)的位置分量；vx，vy和vz為火箭在發(fā)射坐標(biāo)系內(nèi)的速度分量；D和L分別為無量綱化的阻力加速度和升力加速度；ax、ay和az分別為無量綱化的推力加速度在發(fā)射坐標(biāo)系內(nèi)的分量；θ和σ分別為火箭的彈道傾角和彈道偏角；r為火箭的地心矢徑；gx，gy和gz分別為無量綱化的引力加速度在發(fā)射坐標(biāo)系內(nèi)的分量；aek.x，aek.y和aek.z分別為無量綱化的離心加速度和哥氏加速度在發(fā)射坐標(biāo)系內(nèi)的分量。

(2)

(3)

式中，ρ為大氣密度；v為火箭在發(fā)射坐標(biāo)系內(nèi)的合速度；Sref為火箭氣動(dòng)參考面積；m為火箭質(zhì)量；Cx和Cy分別為氣動(dòng)阻力系數(shù)和升力系數(shù)；Pe為發(fā)動(dòng)機(jī)推力；φ和ψ分別為火箭的俯仰姿態(tài)角和偏航姿態(tài)角。

級間無動(dòng)力滑行段和動(dòng)力飛行段的氣動(dòng)力對入軌點(diǎn)參數(shù)的影響較為明顯，因此在確定級間無動(dòng)力滑行段時(shí)間時(shí)需要考慮氣動(dòng)力的影響。為提高計(jì)算效率，采用氣動(dòng)力擬合方式引入氣動(dòng)影響。為統(tǒng)一氣動(dòng)力數(shù)據(jù)擬合表達(dá)式，保證擬合形式的一致性，建立式(4)所示的氣動(dòng)力系數(shù)擬合函數(shù)模型。

(4)

式中，h，Ma，α分別為火箭飛行高度、馬赫數(shù)和攻角；c0，c1，c2，c3，c0′，c1′，c2′，c3′，c0″，c1″，c2″和c3″為氣動(dòng)力系數(shù)擬合系數(shù)。

在滿足數(shù)值預(yù)測精度的情況下，為進(jìn)一步提高數(shù)值預(yù)測效率，采用式(5)所示的線性化引力模型。

(5)

對于火箭所受的推力，需要區(qū)分級間無動(dòng)力滑行段及動(dòng)力飛行段過程，推力Pe的表達(dá)式為

(6)

式中，PT(t)為火箭發(fā)動(dòng)機(jī)高空推力；sm為火箭發(fā)動(dòng)機(jī)噴管出口面積；P(h)為火箭飛行高度對應(yīng)的大氣壓；thx為級間無動(dòng)力滑行時(shí)間；Ts為級間無動(dòng)力滑行后動(dòng)力飛行段的發(fā)動(dòng)機(jī)額定工作時(shí)間。

2 級間無動(dòng)力滑行時(shí)間數(shù)值預(yù)測方法

級間無動(dòng)力滑行時(shí)間的長短將直接影響火箭的后續(xù)飛行狀態(tài)。在滿足入軌點(diǎn)高度和當(dāng)?shù)貜椀纼A角終端約束的情況下，為減小飛行軌跡散布和級間無動(dòng)力滑行后動(dòng)力飛行段的攻角指令大小，改善火箭飛行力熱環(huán)境，通過數(shù)值預(yù)測方法對級間無動(dòng)力滑行時(shí)間進(jìn)行在線計(jì)算。

在線確定級間無動(dòng)力滑行時(shí)間時(shí)，作如下約定：

1)級間無動(dòng)力滑行段火箭按零攻角飛行；

2)第一次預(yù)測級間無動(dòng)力滑行時(shí)間時(shí)，假設(shè)級間滑行后的動(dòng)力飛行段火箭按零攻角飛行；

3)第二次及后續(xù)迭代預(yù)測級間無動(dòng)力滑行時(shí)間時(shí)，級間滑行后的動(dòng)力飛行段攻角在最大值約束范圍內(nèi)，即

|α|≤αmax

(7)

4)級間無動(dòng)力滑行時(shí)間thx在區(qū)間[ta,tb]內(nèi)變化，ta由無動(dòng)力滑行段結(jié)束后的動(dòng)力飛行段姿態(tài)控制起控條件離線確定，tb由入軌點(diǎn)高度約束離線確定。

根據(jù)入軌點(diǎn)參數(shù)要求，以及狀態(tài)方程式(1)，級間無動(dòng)力滑行時(shí)間預(yù)測模型為

(8)

式中，vf和rf分別為預(yù)測的火箭入軌點(diǎn)速度和地心矢徑的大小；v0和r0分別為火箭級間無動(dòng)力滑行開始點(diǎn)的速度和地心矢徑的大小。

根據(jù)飛行軌跡數(shù)值預(yù)測方程式(8)和狀態(tài)方程式(1)，為實(shí)現(xiàn)入軌點(diǎn)參數(shù)約束，需要確定的變量為級間無動(dòng)力滑行thx和推力矢量方向xp。由于thx與xp耦合，因此需要迭代計(jì)算求解。xp的表達(dá)式為

xp=[cosφcosψsinφcosψ-sinψ]T

(9)

在進(jìn)行級間無動(dòng)力滑行時(shí)間預(yù)測時(shí)，需要滿足以下幾點(diǎn)：

1)火箭制導(dǎo)過程處于上升飛行段

為保證火箭制導(dǎo)過程處于上升飛行段，應(yīng)使得當(dāng)?shù)貜椀纼A角Θ不小于0[4-8]。在進(jìn)行級間無動(dòng)力滑行時(shí)間預(yù)測時(shí)，首先假設(shè)火箭級間滑行后的動(dòng)力飛行段按零攻角飛行，則在無動(dòng)力滑行時(shí)間迭代區(qū)間[ta,tb]內(nèi)，只要迭代區(qū)間兩端點(diǎn)對應(yīng)的后續(xù)動(dòng)力飛行段當(dāng)?shù)貜椀纼A角始終不小于0即可，即

(10)

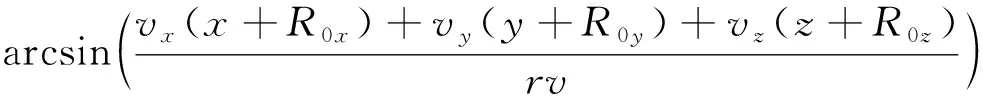
(11)

若式(10)不滿足，則在級間滑行后的動(dòng)力飛行段加入攻角修正，直至滿足式(10)要求，進(jìn)而得到級間滑行后動(dòng)力飛行段的攻角α0。α0作為后續(xù)求解滿足入軌點(diǎn)高度和當(dāng)?shù)貜椀纼A角約束的攻角初值。

2)入軌點(diǎn)高度約束

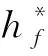
(12)

3)入軌點(diǎn)當(dāng)?shù)貜椀纼A角約束

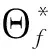
(13)

4)飛行過程中的攻角約束

由于在飛行過程中對火箭的攻角有最大值約束，因此，在進(jìn)行數(shù)值預(yù)測時(shí)，如果預(yù)測出的攻角大于約束條件，則需要對其進(jìn)行限幅，具體如式(14)所示。

(14)

5)反饋增益系數(shù)調(diào)節(jié)

當(dāng)引入偏差時(shí)，實(shí)際飛行軌跡會(huì)偏離預(yù)測軌跡，此時(shí)通過加入反饋環(huán)節(jié)修正偏差[9-11]。即

φ=φ0+kφ·(θ-θ*)

(15)

式中，kφ為反饋增益系數(shù)；θ*為標(biāo)準(zhǔn)軌跡對應(yīng)的彈道傾角；θ為實(shí)際飛行軌跡對應(yīng)的彈道傾角；φ0為標(biāo)準(zhǔn)軌跡對應(yīng)的俯仰角。

綜上所述，級間無動(dòng)力滑行時(shí)間在線數(shù)值預(yù)測的流程為：首先對級間無動(dòng)力滑行時(shí)間加以限制，即thx∈[ta,tb]，并通過迭代求解級間滑行后動(dòng)力飛行段的攻角α0，使得火箭制導(dǎo)過程始終處于上升飛行段，即使得當(dāng)?shù)貜椀纼A角不小于0；然后對級間無動(dòng)力滑行時(shí)間thx進(jìn)行迭代，當(dāng)級間無動(dòng)力滑行時(shí)間為thxc時(shí)，入軌點(diǎn)高度滿足約束條件。最后，進(jìn)一步調(diào)整無動(dòng)力滑行后動(dòng)力飛行段攻角，使得α=αc時(shí)入軌點(diǎn)當(dāng)?shù)貜椀纼A角滿足約束條件。通過上述運(yùn)算，得到滿足入軌點(diǎn)高度、當(dāng)?shù)貜椀纼A角等參數(shù)約束的級間無動(dòng)力滑行時(shí)間thxc及攻角指令αc。

通過數(shù)值預(yù)測得到級間無動(dòng)力滑行時(shí)間后，同步預(yù)測得到級間無動(dòng)力滑行結(jié)束點(diǎn)的當(dāng)?shù)貜椀纼A角Θ(thx)，飛行控制時(shí)，采用Θ(thx)作為無動(dòng)力滑行結(jié)束的判據(jù)進(jìn)行軌跡控制，即滿足下式。

Θ(t)≤Θ(thx)

(16)

級間無動(dòng)力滑行時(shí)間數(shù)值預(yù)測制導(dǎo)流程如圖1所示。

圖1 級間無動(dòng)力滑行時(shí)間在線計(jì)算流程圖

3 仿真分析

采用蒙特卡洛打靶方法分別對傳統(tǒng)離線級間無動(dòng)力滑行時(shí)間計(jì)算方法和基于數(shù)值預(yù)測的在線自適應(yīng)級間無動(dòng)力滑行時(shí)間計(jì)算方法對固體運(yùn)載火箭上升段的控制效果進(jìn)行了對比。通過分析，在滿足入軌點(diǎn)參數(shù)精度要求的情況下，基于數(shù)值預(yù)測的在線自適應(yīng)級間滑行時(shí)間計(jì)算方法大幅減小了動(dòng)力飛行段攻角，縮小了飛行過程高度、當(dāng)?shù)貜椀纼A角等軌跡散布，驗(yàn)證了所提方法的有效性。

4 結(jié)論

闡述了基于數(shù)值預(yù)測的固體火箭級間無動(dòng)力滑行時(shí)間在線計(jì)算方法，通過仿真分析，獲得以下結(jié)論：

1)采用擬合氣動(dòng)力和線性化引力等簡化措施，在提高軌跡數(shù)值積分預(yù)測效率的同時(shí)，可滿足軌跡預(yù)測精度的要求；

2)采用基于數(shù)值預(yù)測的級間無動(dòng)力滑行時(shí)間在線自適應(yīng)計(jì)算方法，在滿足入軌點(diǎn)參數(shù)精度要求的情況下，對改善火箭飛行力熱環(huán)境和減小入軌點(diǎn)速度損失有重要作用。通過仿真分析，驗(yàn)證了所提方法的有效性，具有較好的應(yīng)用價(jià)值。