自抗擾fal函數的改進及在無拖曳衛星中的應用

喬鑫宇 周文雅 吳國強

大連理工大學航空航天學院，大連 116024

0 引言

空間科學任務對太空實驗環境要求越來越嚴格，航天器所受到的自身擾動、大氣阻力以及太陽輻射等空間擾動成為影響實驗結果的重要因素[1-2]。無拖曳衛星以檢驗質量塊作為跟蹤點，通過微推進器對衛星本體進行連續主動控制，補償航天器和檢驗質量塊之間的受攝差，來營造超靜超穩的空間實驗環境[3-5]，在廣義相對論的驗證以及重力場的測量等領域有著十分重要的應用。但由于空間環境中擾動及噪聲復雜，存在極大的不確定性，要想實現其瞬態性能和魯棒性能的協調控制還存在諸多理論和技術上的困難[6-12]。

由韓京清研究員提出的自抗擾控制(Active Disturbance Rejection Control, ADRC)算法[13]是將控制對象視為積分串聯型，利用擴張狀態觀測器(Extended State Observer，ESO)對動態對象中異于標準型的部分進行實時估計和補償，來抑制擾動對系統輸出的影響。由于算法對參數和結構變化展現出的強自適應能力和穩健的魯棒性，使其在無拖曳衛星控制器的設計上占據一席之地[14-18]。

作為自抗擾控制器的重要部件，擴張狀態觀測器的性能直接影響著自抗擾控制器的性能[19-20]。而作為擴張狀態器重要組成部分，fal函數直接影響著擴張狀態觀測器性能的好壞。現有的fal函數在收斂性能上還存在著很大的提升空間[21-22]。為了進一步提升控制器的控制性能，降低殘余加速度噪聲，本文提出了faln函數，并對其穩定性進行了理論論證，同時與現有的fal函數形式進行比較。

1 模型介紹

無拖曳衛星的工作原理是：通過控制系統保證衛星本體和檢驗質量塊保持相對靜止的運動狀態。由于檢驗質量塊處于完全保守力環境，從而保證衛星處于 “無拖曳狀態”[23-24]。

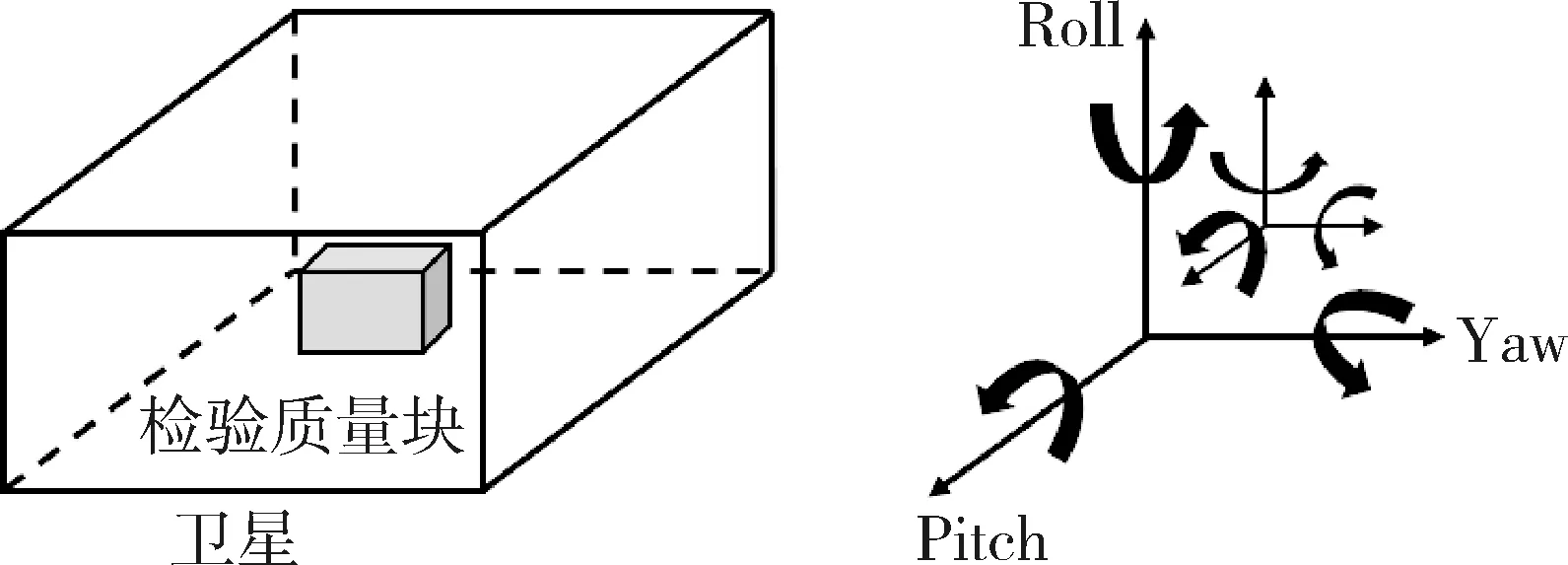
圖1 無拖曳衛星控制系統框圖

下面給出簡化后衛星本體的姿態動力學、相對軌道動力學以及相對姿態動力學模型。

(1)

(2)

(3)

其中，φsc指衛星本體的姿態角，TCsc表示作用在衛星本體上的控制力矩，ωTCsc表示與TCsc對應的輸入噪聲，TDsc表示作用在衛星本體上的擾動力矩，rrel表示衛星本體和檢驗質量塊間的相對位移，FCsc表示作用在衛星本體上的控制力，ωFCsc表示與FCsc對應的輸入噪聲，FDsc表示作用在衛星本體上的擾動力，φrel表示衛星本體和檢驗質量塊間的相對姿態角，φtm表示檢驗質量塊的姿態角，TCtm表示作用在檢驗質量塊上的控制力矩，ωTCtm表示與TCtm對應的輸入噪聲，TDtm表示作用在檢驗質量塊上的擾動力矩，上述介紹的都是在X，Y，Z方向或俯仰(Pitch)、偏航(Yaw)、滾動(Roll)方向上有分量的三維向量；Isc為衛星的慣量陣，Itm為檢驗質量塊的慣量陣，Krot、Drot為衛星與測試質量間的旋轉耦合系數，I3為單位矩陣，上述介紹的都是3維矩陣；msc為衛星質量，mtm為檢驗質量塊的質量。

在無拖曳控制中，衛星內部執行機構產生的噪聲和衛星的設計息息相關，一般需要其具有很高的精度并同時可以提供相對較大的推力范圍。通常為了考慮推力器的未知性能，模型需包含一定不確定性。

2 擴張狀態觀測器

自抗擾控制器主要由微分跟蹤器、非線性組合PID、擴張狀態觀測器、以及擾動補償等4部分構成，其結構如圖2所示。

圖2 自抗擾控制器框圖

微分跟蹤器作用是根據控制對象的承受能力安排過渡過程v1并提取設定值v的微分信號v2；非線性組合PID的設計理念是“大誤差小增益，小誤差大增益”，提升控制效果同時避免執行機構飽和；擴張狀態觀測器的輸出z1，z2和z3是根據輸出y和輸入信號u對控制對象狀態x1，x2以及總擾動x3的估計；最終控制量u是由擾動估計值z3和誤差反饋控制量u0共同決定。

傳統形式的fal函數是將冪函數改造成在原點附近有線性段的連續非光滑的函數，其表達式如下所示。

(4)

其中，e0是fal0函數變量，一般指的是觀測器對輸出量的估計誤差；a是0～1之間的常數，h是影響濾波效果的常數。這樣的非光滑函數形式既可以保證誤差快速歸于0，也可以避免在誤差較小的時候擴張狀態觀測器的高頻震蕩現象，在提高控制精度的同時，保證系統穩定性。因此，設計合適的fal函數形式對于提高自抗擾控制器的性能具有深遠意義。

3 fal函數的改進

3.1 faln函數

fal0函數并不是在所有應用場合下都具有最優的控制效果[25]，眾多學者從不同的角度提出了其改進形式。

陳志旺[26]等提出fal1函數形式，并將其應用于四旋翼飛行控制系統。經過仿真驗證，系統抵抗外界強干擾的能力增強。

(5)

趙海香[27]提出fal2函數形式。

(6)

其中，k1為線性反饋部分的增益；ec是從非線性到線性反饋的誤差閾值，可根據實際系統控制量特性以及控制器選取的增益系數進行適當設置。a值越小，非線性段系統反饋增益越小，系統抑制擾動的性能越好。然而，a值的減小會限制系統的控制能力，導致系統誤差較大時無法快速有效地利用控制量，最終影響控制系統性能。由于無拖曳衛星的運行環境復雜，不確定性較高，因此需要控制系統具有協調控制性能和魯棒性能的能力。本文基于指數函數對fal函數進行改進，改進后的fal函數為

faln(e0,a,h)=

(7)

其中，k2為指數項的誤差增益，可以根據實際需要進行選取，通常采用較小的正數。

不難發現，相較于現有的fal函數，本文所設計的faln函數增益量適中，以保證在控制系統穩態精度不受太大影響的前提下，盡可能地提高控制系統的收斂速度。

3.2 faln函數穩定性分析

觀測器的誤差方程為如下形式，

(8)

其中，e是觀測器對狀態量的觀測誤差，e1是對狀態量x1的觀測誤差。

本文借助文獻[28]所提出的系統穩定性理論來證明使用faln函數的ESO可以完成系統的狀態觀測。其證明過程借助了如下引理：

引理1如果存在主對角元素為正數的斜對稱矩陣D

(9)

使得DA(e1)對稱正定，則系統是Lyapunov漸近穩定的。假定d11=1，d22=d33=ε>0以滿足主對角線元素為正數的要求。

通過計算計算可得

(10)

其中，

D11=d11β01+d12β02F+d13β03F,

D21=-d12β01+d22β02F+d23β03F,

D11=-d13β01-d23β02F+d33β03F,

那么DA(e1)滿足的對稱正定性條件如下，

D11=β01+εβ02F+εβ03F>0

(11)

(12)

D11(d12d23-ε2)-2d12ε-d123-d23>0

(13)

其中，B=(β01β02-β03)。

以下需證明存在矩陣D，使上述不定式成立。

由于引理要求矩陣的存在性，因此考慮式(11)成立的必要條件如式(14)所示。

(14)

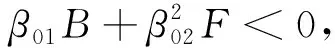
由矩陣的對稱性要求可將式(12)和式(13)整理成如下形式。

(15)

β01β02-B>0

(16)

由于B=(β01β02-β03)>0，上式成立。

綜上，當D矩陣滿足條件B=(β01β02-β03)>0時，可以找到使DA(e1)是對稱正定的D矩陣，而系統狀態的改變，并不會影響系統的漸進穩定性，由此證明使用faln函數的ESO可以完成系統的狀態觀測。

4 仿真試驗及結果

4.1 無拖曳衛星faln自抗擾算法驗證實驗

為了驗證設計的控制系統對于外界擾動的補償效果，分析系統的控制精度，對系統進行仿真實驗。系統模型(1)～(3)中的參數取自文獻[23]-[24]，具體設定如下文表述以及表1所示。

表1 衛星仿真參數

假定ωTCSC和ωFCSC的功率譜密度均為10-8m·s-2·Hz-0.5，ωTCtm的功率譜密度為10-15m·s-2·Hz-0.5，干擾力與力矩具有正弦性質，頻率為ωd。

本文從衛星本體和檢驗質量塊的相對位置、相對姿態等方面對這兩種方式進行比較。

4.2 數值仿真

無拖曳衛星在運行過程中可能會受到來自環境的大幅度干擾或者需要采取主動位置姿態調整，這兩種情況都會導致檢驗質量塊和衛星本體出現瞬時位置和姿態偏差。此時擴張狀態觀測器的狀態估計誤差瞬時變大，fal函數大誤差段的函數形式會直接影響狀態估計性能。

綜上所述，本文重點分析偏差后衛星本體和檢驗質量塊的運行狀態以及擴張狀態觀測器的狀態估計情況，說明本文提出的faln函數在無拖曳衛星控制方面的優勢。不失真實性和一般性，假定衛星本體和檢驗質量塊相對距離初始值為rrel0=[0.1 0.3 0.2]Tm，相對姿態角初始值為φrel0=[0.1 0.3 0.2]Trad。

圖3 x軸相對位置觀測誤差曲線

上圖給出的是4種ESO對于x軸的相對位置rx的觀測誤差曲線，可以直觀看到基于faln函數的ESO具有更快的觀測誤差收斂速度和更加平穩的收斂過渡過程。

實際上，fal1函數以犧牲控制性能保證控制系統的魯棒性，然而無拖曳衛星質量較大且運行時所受環境擾動相對于大氣環境較小，因而其優勢無法得到體現，在相對位置和姿態仿真曲線中收斂速度較慢，甚至出現發散情況。因而本文主要針對基于fal0、fal2和faln的控制器性能進行比較。

圖4和5給出的是衛星本體和檢驗質量塊的x軸相對位置rx及pitch軸相對姿態φpitch的數值仿真情況，其他兩軸的位置姿態調節曲線與其類似，本文不再給出。仿真結果顯示，基于faln函數的控制器收斂速度最快，能夠實現最快速的三軸相對位置和姿態穩定。

圖4 x軸相對位置變化曲線

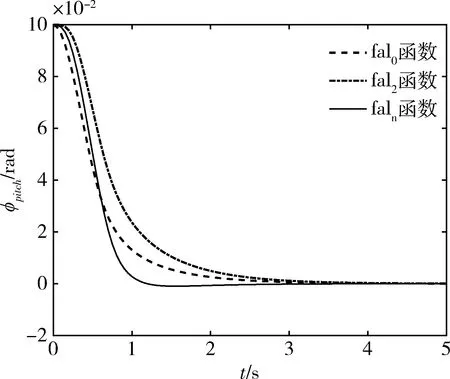
圖5 Pitch軸相對姿態變化曲線

圖6給出的是基于faln函數的無拖曳控制系統三軸線性殘余加速度功率譜密度的擬合曲線。其中z軸達到10-13m·s-2·Hz-0.5量級，x和y軸能夠達到10-14m·s-2·Hz-0.5，在數值仿真實驗上，能夠和LISA-Pathfinder達到相同水平。

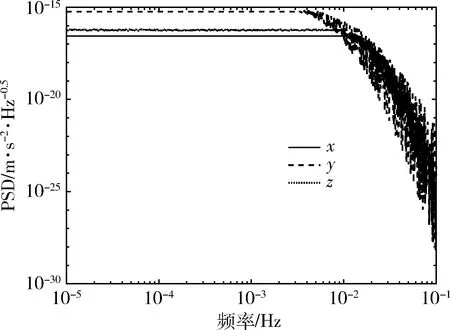
圖6 衛星和檢驗質量塊線性殘余加速度功率譜密度

以上仿真結果證明了基于faln函數的無拖曳控制器在保證衛星穩定運行的情況下，提高了ESO的觀測性能，同時縮短了無拖曳衛星位姿調整時間，加快了控制系統運行效率。

5 結論

本文的研究重點在于如何通過改進自抗擾fal函數，來提高擴張狀態觀測器對無拖曳衛星的位姿狀態的觀測能力，從而使無拖曳控制系統控制過程更加平穩、快速。基于此目標，本文提出了faln函數。在通過數學理論證明其穩定性后，完成了與現有的fal函數形式的對比分析。數值仿真實驗證明基于faln函數的無拖曳控制器具有更好的狀態估計性能和更快速更穩定的過渡過程，更適用于無拖曳衛星的位姿控制。

接下來的首要工作是如何進一步改進狀態觀測器的狀態估計性能，使得誤差曲線更加平滑。此外，目前大部分的fal函數改進算法側重于大誤差段的函數改進，無法改進控制系統的穩定狀態。如何設計出一種更大范圍的fal函數改進形式，使其具有更好的穩態性能。對于提升自抗擾控制器的控制性能具有十分重要的意義。