分部積分在分數階微積分逼近的誤差估計中的應用
張光輝,任 敏
(宿州學院 數學與統計學院,安徽 宿州 234000)
分數階微分方程由于自身理論的迅速發展,在數學、物理、化學、控制理論及金融等各學科中得到了廣泛的關注和應用[1-7],為描述不同物質的記憶和傳承性質提供了有力工具.隨著分數階微分方程應用的不斷深入,分數階微積分的數值運算和數值模擬[8]必不可少,尤其是在時間分數階偏微分方程的數值計算中,時間初始奇異性問題普遍存在,對分數階微積分算子合理有效地逼近是建立高效差分格式的關鍵技術[9].本文基于積分型余項的泰勒公式,給出了在分數階微積分的數值分析中應用廣泛的插值逼近[10]和半點逼近等幾個逼近格式的誤差估計,并用分部積分進行了證明.
1 預備知識
定義1Riemann-Liouville積分[11]
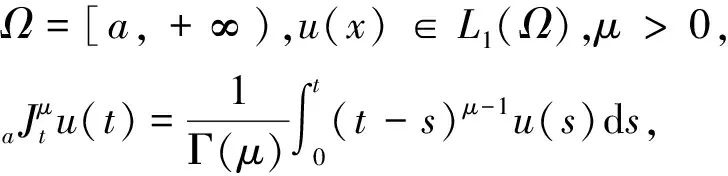
稱為右側μ階Riemann-Liouville分數階積分.
引理1[12]對t0,t∈[0,T]和任意的n∈N,若函數u(t)∈C(n+1)[0,T],則有:
(1)
2 主要結果
在分數階微分或偏微分方程的數值計算中,對微積分算子中的積分項進行逼近時,經常需要用到插值近似,下面給出幾個插值逼近的積分型誤差余項.
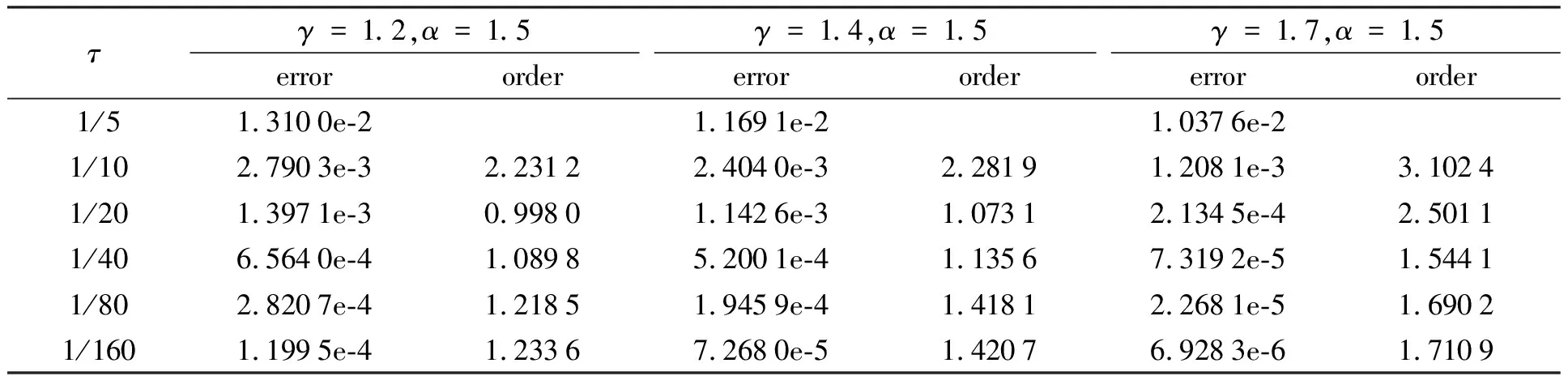
定理1若函數u(t)∈C(k+1)[0,T],0=t0 設u(t)關于tk-1,tk(1≤k≤N)的一次插值多項式為: 則用P1,ku(t)逼近u(t)的積分型誤差估計式為: (2) 證明:由引理1的積分型余項taylor公式,u(t)在tk-1處有展開式: (3) 在(3)式中,令ξ=tk-1+s(t-tk-1),s∈[0,1],則(3)式化為: (4) 利用分部積分,對(4)式右端積分項進一步計算,有: (5) 類似的,在區間[t,tk]上,應用引理1有: (6) 從(6)式中解出u′(t),代入(5)式,有: (7) 對(7)進一步整理,得到(2),則定理1得證. 定理2若函數u(t)∈C(k+1)[0,T],0=t0 設u(t)關于tk-2,tk-1,tk(2≤k)的二次插值多項式為: 則當t∈(tk-1,tk)時,用P2,ku(t)逼近u(t)的積分型誤差估計式為: (8) 證明:由引理1的型積分余項taylor公式,u(t)在tk-1處有展開式: (9) (10) 利用分部積分,計算(10)式右端第一項積分,有: 類似地,利用分部積分計算(10)式右端第二項積分,有: =(t-tk-1)2u″(t)-(t-tk-1)u′(t)+(t-tk-1)u′(tn-1). 將Q1、Q2的計算結果代入(10)式,得到: (11) 類似于得出(11)式的推導過程,u(t)在tk-2、tk處分別有: (12) (13) 將(11)~(13)聯立,消去u′(t)、u″(t),得到(8)式,定理2得證. 推論1 若函數u(t)∈C(k+1)[0,T],0=t0 設u(t)關于tk-3,tk-2,tk-1(3≤k)的二次插值多項式為: (14) 證明:類似于證明定理2的步驟,易得(14)式. 在時間分數階微分偏微分方程的離散過程中,在半點處建立差分格式是常用技巧,下面給出一個半點處積分算子的計算公式. (15) (16) 對g(t)求二階導數,得: 其中C為通用常數. u(0)=u′(0)=0,故由taylor定理,(15)式成立. (17) 證明:在定理3中,令λ→2,易得(17)式成立. (18) 其中右端源像: g(u)=u3,方程(18)具有解析解u(x,y,t)=tγsin(πx)sin(πy). 先將方程(19)轉化為等價的分數階積分-微分方程: (19) 應用(15)和(8)對(19)進行數值離散和誤差估計,可建立一個求解(18)的ADI格式,并得到截斷誤差在時間方向的階為O(τγ),其中τ為t方向的離散步長. 取T=1,α=1.5,h1=h2=0.001,分別取不同的γ和不同的時間步長τ,計算ADI格式對于不同的γ,當t=t1=τ時所得數值解的誤差和時間方向的收斂階,計算結果見表1. 表1 固定h=0.001時,ADI格式在t=t1=τ的誤差和時間方向收斂階 該數值算例驗證了ADI格式在時間方向臨近初始時刻的收斂階逼近γ,即截斷誤差時間方向的階為O(τγ),從而驗證了本文推導的理論公式應用的有效性. 在分數階微分方程,尤其是分數階偏微分方程的數值計算中,對方程中積分項的合理有效逼近是構造高精度收斂格式的重要技術和環節,文中對數值分析中常用的一、二次插值逼近和半點逼近方法的誤差估計,在對分數階微積分算子積分項的逼近計算中有著廣泛的應用,是構造和分析求解分數階偏微分方程,尤其是時間分數階偏微分方程差分格式的有力工具.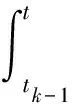
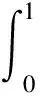
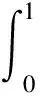
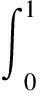
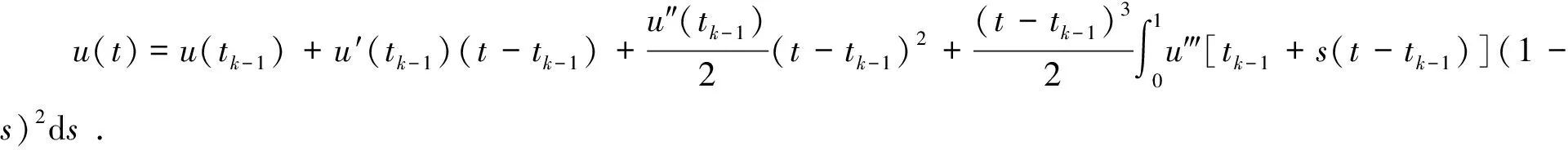
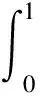
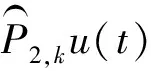
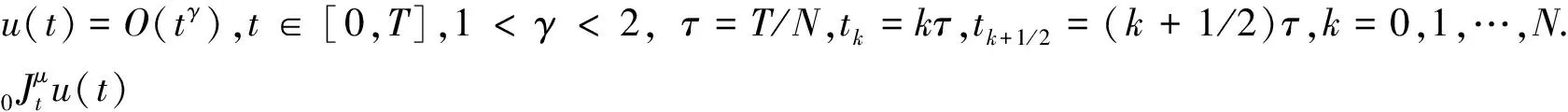
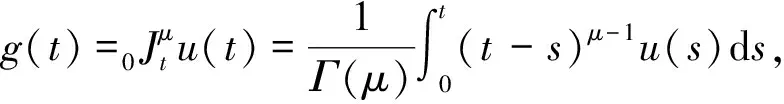
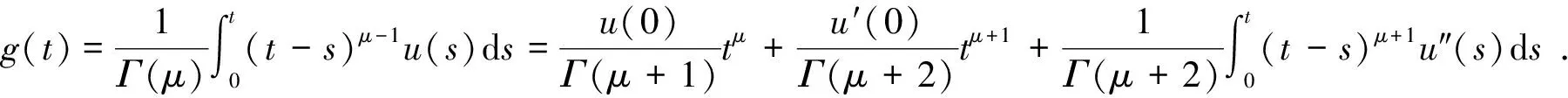
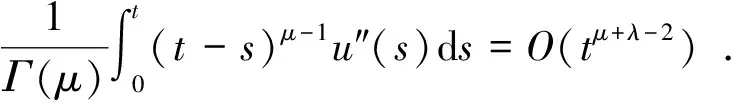
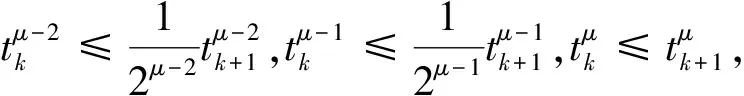
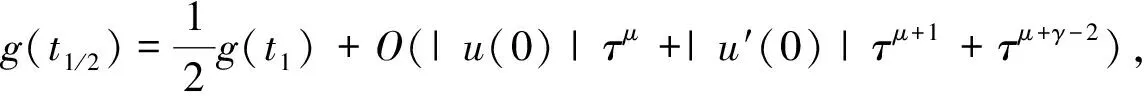
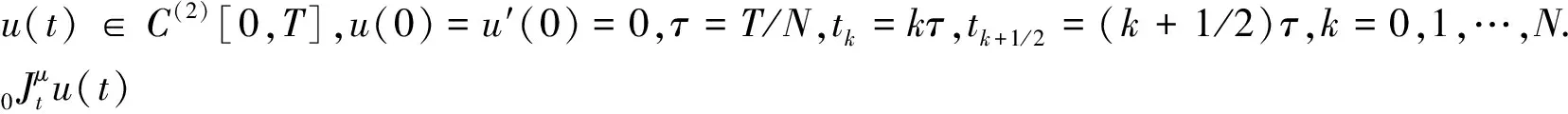
3 算例分析
4 結 論

