基于改進避障策略和雙優化蟻群算法的機器人路徑規劃

郝 琨 張慧杰 李志圣 劉永磊

(天津城建大學計算機與信息工程學院， 天津 300384)

0 引言

隨著科技的發展，移動機器人已經被廣泛應用于地面自主導航[1]、水下環境勘探[2]、應急信息采集[3]等領域中。路徑規劃技術是實現移動機器人智能化的關鍵技術之一，它是指移動機器人根據一種或多種性能指標，在復雜的空間環境中，尋找一條從起點到終點且沒有碰撞的最優或次優路徑[4-5]。目前移動機器人路徑規劃的主流算法分為兩大類：傳統算法與仿生學智能算法。其中，傳統算法主要有A*算法、人工勢場法等。智能算法主要有遺傳算法、蟻群算法、粒子群算法、免疫算法等[6-8]。傳統算法在簡單的地圖環境中性能較好，但不適用于復雜的地圖環境中。而智能仿生學算法則存在過早收斂、易陷入局部極值等問題[9]。

蟻群算法具有良好的并行性和魯棒性，因此被廣泛地應用于路徑規劃領域[10-12]。但蟻群算法在路徑規劃領域也存在前期搜索盲目、收斂速度慢、容易陷入局部最優和死鎖等問題。文獻[13]利用人工勢場法修改了蟻群算法的啟發值參數，并提出了吸引素使蟻群算法更快收斂。文獻[14]提出了一種基于合作博弈機制的多蟻群協同優化算法(CCACO)來加快算法的收斂速度，但該算法在大規模地圖中運行效率低。文獻[15]將人工勢場法與蟻群算法相結合來提高算法后期的全局搜索能力。并采用基于運動路徑的幾何方法實現動態障礙物避障，但該算法不適合在未知環境下使用。文獻[16]提出了一種改進蟻群算法(Improved ant colony algorithm，IACO)。該算法通過使初始信息素不均勻分布避免算法的早期盲目搜索，加快算法收斂速度，并利用動態懲罰方法減少螞蟻陷入死鎖的數量，但是該方法不能有效解決深度死鎖問題。文獻[17]提出了一種改進雙層蟻群算法，將蟻群劃分為引導層蟻群和普通層蟻群以應對不同的情況。然而，該算法將引導層蟻群與普通蟻群并行進行使引導層蟻群并未起到相應作用。

針對蟻群算法在路徑規劃中存在收斂速度慢、收斂路徑質量低、死鎖以及動態避障能力差的問題，本文提出基于改進避障策略和雙優化蟻群算法(Double optimization ant colony algorithm，DOACO)的路徑規劃方法，該算法通過改進概率轉移函數解決蟻群算法收斂速度慢的問題；通過回溯機制結合路徑長度清零機制解決死鎖問題；并通過路徑優化與精英保存策略進一步提高收斂路徑的質量；同時針對動態環境中的避障問題，提出一種避障行為與局部路徑重規劃相結合的避障策略。

1 空間環境模型

采用柵格法[18]建立空間環境模型，整個二維平面被劃分為20×20大小一致的柵格，如圖1所示。其中，白色柵格表示機器人可活動的自由區域，黑色柵格表示靜態障礙物，紅色柵格表示動態障礙物。黑色柵格和紅色柵格所在區域均為機器人不可活動區域(即障礙物區域)。地圖從左到右、從上到下由1開始為柵格添加編號直到添加至右下角的第400號柵格。環境地圖中各柵格的坐標由其中心點坐標(x,y)表示，柵格編號與柵格坐標之間的轉換式為

圖1 20×20柵格地圖Fig.1 20×20 grid map

(1)

y=n+0.5-ceil(m/n)

(2)

其中

m=floor(l-y)n+ceil(x)

(3)

式中m——柵格編號

n——柵格總列數

l——柵格總行數

(x,y)——柵格的橫、縱坐標

式(1)、(2)把柵格編號轉換成柵格坐標。式(3)把柵格坐標轉換成柵格編號。mod()為取余函數，floor()為向下取整函數，ceil()為向上取整函數。

2 DOACO算法設計

2.1 DOACO算法

DOACO算法參數包括：起點柵格編號S，目標點柵格編號G，最大迭代次數Ncmax，當前迭代次數Nc，蟻群中螞蟻的總數量K，當前螞蟻數量k，信息素常量Q，信息素因子α，啟發式因子β，信息素揮發因子ρ，偽隨機概率調整因子q0。圖2為DOACO算法流程圖，算法流程如下：①對蟻群算法的各參數進行初始化。②令Nc=1。③令k=1。④將第k只螞蟻放置在起點位置。⑤根據改進的概率轉移公式選擇下一個路徑點。⑥判定螞蟻是否陷入死鎖狀態，若陷入死鎖，則采用死鎖處理策略使得螞蟻跳離死鎖，然后轉入步驟⑤；若未陷入死鎖，則更新第k只螞蟻的禁忌表，然后轉入步驟⑦。⑦判斷螞蟻是否到達目標點，若未到達，轉至步驟⑤；若已到達目標點，則轉到步驟⑧。⑧判斷該螞蟻是否為當前迭代次數中的最后一只螞蟻，若不是最后一只螞蟻，則令k=k+1，然后返回步驟④；若是最后一只螞蟻，則更新信息素并判斷Nc>Ncmax是否成立，若不成立則轉入步驟⑨，否則轉入步驟⑩。⑨Nc=Nc+1，同時返回步驟③。⑩輸出收斂路徑，采用路徑優化策略，得到最優路徑，流程結束。

圖2 DOACO算法流程圖Fig.2 Flow chart of DOACO algorithm

2.2 偽隨機概率轉移

本文設計一種新的概率轉移方法，通過引入偽隨機概率調整因子q0來調整概率轉移函數中對優質路徑點的選擇程度(式(4))，避免傳統蟻群算法中選擇優質路徑點的概率過低這一問題(式(5))。

(4)

(5)

τij——路徑點i和路徑點j之間的信息素濃度

ηij——當前路徑點i到路徑點j的啟發式信息

ak——當前路徑點i的下一個可行路徑點的集合

w——通過偽隨機概率轉移函數所獲得的路徑點

Roulette()——利用輪盤賭策略選取路徑點的函數

q——隨機數

q0通常為固定常數，當q≤q0時，保留最優鄰居路徑點。當q>q0時，利用傳統概率轉移方法和輪盤賭策略獲得路徑點。

在傳統概率轉移函數中，假設某優質路徑點被選擇的概率為p，此時引入偽隨機轉移概率因子q0，根據式(5)，設偽隨機概率轉移函數對該優質路徑點的選擇概率為p1，則p1=q0+(1-q0)p，而p1-p=q0-pq0=q0(1-p)≥0，故p1≥p，即引入偽隨機概率調整因子后，新函數中優質路徑點被選擇的程度大于傳統概率轉移函數。在已知p的情況下，新函數對優質路徑點的選擇程度取決于q0，因此，通過引入偽隨機概率轉移因子q0來調整優質路徑點被選擇的概率可行。

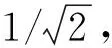
(6)

式中dij——路徑點i和路徑點j之間的距離

針對傳統啟發式信息的問題，本文設計了新的啟發式信息函數，充分考慮下一節點到目標點的關系，強化啟發式信息的引導作用，計算式為

(7)

式中djg——路徑點j和目標點g之間的距離

在迭代前期，信息素對蟻群的引導作用較弱，啟發式信息應發揮主導作用。此時信息素因子應較小，啟發式因子應較大，強化啟發式信息的主導作用。隨著迭代次數的增加，各路徑段上的信息素差異逐漸增大，信息素逐漸發揮主導作用。此時信息素因子逐漸增大，啟發式因子逐漸減小，這樣可以強化信息素的主導作用。基于上述分析，本文設計了自適應信息素因子α1、自適應啟發式因子β1,以加快算法的收斂速度，計算式為

α1=[(Ncmax+Nc)/Ncmax]α

(8)

(9)

2.3 信息素初始化及更新

信息素初始化主要有兩種方式：均勻分布和不均勻分布。初始信息素的不均勻分布[19-20]使算法有傾向性的快速收斂于某一條路徑，當應對復雜地圖環境時極易導致算法陷入局部最優解。而信息素均勻分布可以擴大算法對解空間的搜索范圍，增強算法的種群多樣性，降低算法陷入局部最優解的概率。因此本文采用初始信息素均勻分布的方法。

在信息素更新方面，DOACO僅考慮對每條路徑上的信息素進行單次更新，不考慮二次更新[21-22]。信息素更新過程為

τij(t+1)=(1-ρ)τij(t)+Δτij(ρ∈(0,1))

(10)

其中

(11)

(12)

式中 Δτij——路徑段(i,j)上的信息素增量

Lk——第k只螞蟻所經過的路徑長度

2.4 死鎖問題處理策略

采取回溯機制和路徑長度清零機制相結合的方法來解決蟻群算法的死鎖問題[23]。假設當前螞蟻行進到了第n個路徑點且螞蟻在第n個路徑點處陷入死鎖狀態。則執行該方法流程如下：①令i=n。②將第i個路徑點和第i-1個路徑點之間的路徑標記為不可行狀態(即路徑長度清零機制)。③螞蟻返回到第i-1個路徑點(即回溯機制)，即i=i-1。④判斷螞蟻當前所在路徑點是否陷入死鎖現象。如果螞蟻當前所在路徑點陷入了死鎖現象，則轉入步驟②。如果螞蟻當前所在路徑點沒有陷入死鎖現象，則流程結束。螞蟻根據概率轉移函數選擇下一個路徑點。

該方法通過回溯并將路徑長度清零重新調整螞蟻尋路方向保證螞蟻百分之百的存活率，提高螞蟻對解空間的探索能力。

2.5 路徑優化策略

DOACO算法在收斂路徑的基礎上對收斂路徑進行了二次優化，從而進一步提高收斂路徑的質量，路徑優化策略如下：

(1)定義關鍵路徑點的概念并找到一條收斂路徑中關鍵路徑點的集合。關鍵路徑點是指可以支撐起一條路徑中某一個路徑段的核心路徑點。包括：起點、目標點、特殊的路徑點(多為路徑轉折處及障礙物附近的路徑點)。

(2)利用啟發式策略設計連接操作符。啟發式策略是尋找當前路徑點附近的距離目標點最近的相鄰路徑點。連接操作符是指利用啟發式策略生成兩個路徑點之間的路徑段的操作。

(3)利用連接操作符生成兩個相鄰關鍵路徑點之間的新的路徑段。

(4)若兩個關鍵路徑點之間的新的路徑段比之前的路徑段好，則用新的路徑段取代舊的路徑段。若兩個關鍵路徑點之間新的路徑段比之前的路徑段差，則不作改變。

假設某條路徑中的第i個路徑點是關鍵路徑點，則該條路徑中的下一個關鍵路徑點的尋找方法如下：①令j=i，其中j為指針型變量，用作尋找關鍵路徑點。②令j=j+1。③如果第j個路徑點是終點，則第j個路徑點就是下一個關鍵路徑點，流程結束。否則，轉入步驟④。④如果第i個路徑點到第j個路徑點之間的連線不經過障礙物柵格且第i個路徑點到第j+1個路徑點之間的連線經過障礙物柵格，則第j個路徑點就是下一個關鍵路徑點，流程結束。否則，轉入步驟②。

本文使用二維柵格地圖中的碰撞檢測模型[24]來檢測兩個路徑點之間的連線是否與障礙物柵格發生碰撞。

3 動態避障

針對傳統避障策略存在的避障能力較差且實時性不足的問題[25-26]，本文利用避障行為中的等待策略，并結合局部路徑重規劃的方法來進行動態避障。局部路徑重規劃方法是指當預測到移動機器人和動態障礙物即將碰撞時，利用啟發式策略重新生成碰撞處的局部路徑段的方法，該方法僅對全局路徑進行小幅度調整。因此局部路徑重規劃方法具有避障代價小、避障實時性強、路徑質量高的優點。

3.1 碰撞類型

按照不同的碰撞方式將碰撞類型分為正面碰撞、側面碰撞以及障礙物停留在全局路徑上的靜態碰撞。其中，正面碰撞又分為接觸式正面碰撞和非接觸式正面碰撞。正面碰撞是指移動機器人與動態障礙物因運動方向共線且相反而產生的面對面碰撞的情況。假設移動機器人當前位置為ri(rix,riy)，移動機器人下一個位置為ri+1(ri+1x,ri+1y)。動態障礙物當前位置為oi(oix,oiy)，動態障礙物下一個位置為oi+1(oi+1x,oi+1y)。

若移動機器人與動態障礙物發生正面碰撞時有公共碰撞點，則這種碰撞情況被稱為非接觸式正面碰撞(圖3a)。即

圖3 碰撞類型示意圖Fig.3 Schematic of collision types

(13)

若移動機器人與動態障礙物發生正面碰撞時沒有公共碰撞點，即移動機器人與動態障礙物的下一步互為行進柵格。在這種情況下雖無碰撞點但兩者也會發生碰撞，這時判斷這種碰撞情況為接觸式正面碰撞(圖3b)。即

(14)

側面碰撞是指移動機器人與動態障礙物運動方向不共線，但在某一時刻兩者恰好產生公共碰撞點的情況(圖3c)。即

(15)

障礙物停留在全局路徑上的靜態碰撞是指動態障礙物由于某種原因恰好停留在了全局路徑上，導致移動機器人與障礙物必定會發生碰撞的情況。即

(16)

3.2 避障策略

本文提出的動態避障策略包含兩種避障策略：原地等待策略和局部路徑重規劃策略。針對側面碰撞，采取等待策略來避免碰撞的發生。即在側面碰撞發生前，移動機器人原地暫停，等待動態障礙物通過后移動機器人再繼續前進。

針對接觸式正面碰撞、非接觸式正面碰撞及障礙物停留在全局路徑上的靜態碰撞，采取局部路徑重規劃策略來避免碰撞的發生。假設移動機器人位于全局路徑的第i個路徑點，則把預測的公共碰撞點視為靜態障礙物并利用啟發式策略重新規劃第i個路徑點到第i+2個路徑點之間的局部路徑。當移動機器人沿著局部路徑避過障礙物后，移動機器人將會重新返回全局路徑。

4 仿真實驗

4.1 仿真設計

為了驗證DOACO算法的性能，本文將DOACO算法、ACO算法、IACO算法[16]分別運行在人工仿真的20×20柵格地圖與自然環境仿真圖書館的50×50柵格地圖下進行比較。20×20柵格地圖環境為人為設置，而50×50柵格地圖以真實圖書館環境為原型設置。評價指標包括：路徑生成、路徑長度、算法收斂所需的迭代次數、算法收斂所需的程序運行時間、螞蟻存活率等。另外，通過在上述自然仿真的50×50地圖中增加不同時間、不同方向出發的動態障礙物模擬圖書館中的學生來驗證動態避障策略的有效性。

4.2 人工仿真實驗

人工仿真實驗使用20×20的柵格地圖(圖1)，單位柵格長度設為1 m，移動機器人從1號柵格進入，從400號柵格離開。蟻群算法初始參數如表1所示。

表1 蟻群算法初始參數Tab.1 Parameters of ant colony algorithm

4.2.1路徑生成

圖4為ACO算法和IACO算法的機器人運動軌跡圖。從圖4a可看出，ACO算法生成路徑的質量明顯較差，而IACO算法生成的路徑(圖4b)質量有了一定的提高。圖5為未添加優化策略的DOACO算法和添加優化策略的DOACO算法的機器人運動軌跡圖。從圖5a可看出，未添加優化策略的DOACO算法由于改進了啟發信息等以及使用精英保存策略，生成路徑的質量明顯提高，但是該路徑仍有進一步優化的空間。從圖5b可看出，添加優化策略的DOACO算法生成路徑的質量最好。實驗結果表明，DOACO算法生成的路徑明顯優于ACO算法和IACO算法。

圖4 機器人運動軌跡圖Fig.4 Robot motion trajectory diagrams

圖5 DOACO算法的機器人運動軌跡圖Fig.5 Robot motion trajectory diagrams of DOACO algorithm

4.2.2收斂曲線分析

圖6為3種算法的收斂曲線。從圖6可看出ACO算法在108代收斂，收斂后的最優路徑長度為37.8 m。IACO算法在41代收斂，收斂后的最優路徑長度為37.56 m，該算法采用改進信息素的初始分布，因此收斂次數減少。而DOACO算法在15代就已經收斂，收斂后的最優路徑長度為34.38 m。從收斂路徑長度和收斂迭代次數來看，DOACO算法優于ACO算法和IACO算法，這主要是由于DOACO采用了路徑優化策略以及改進的概率轉移函數。此外，從圖6中還可以發現，ACO算法和IACO算法均存在數據回落現象，而DOACO算法由于采用了精英保存策略，有效避免了數據回落現象。

圖6 3種算法收斂曲線Fig.6 Comparison of convergence curves of three algorithms

4.2.3螞蟻存活率分析

3種算法的螞蟻存活率變化曲線如圖7所示。從圖7可以看出，在100代之前，隨著迭代次數的增加，ACO算法的螞蟻存活率呈逐漸上升趨勢。在100代之后，ACO算法的螞蟻存活率會有波動，但是總體上穩定。IACO算法則是在93代之前，隨著迭代次數的增加，螞蟻的存活率逐漸上升。到了93代之后，螞蟻存活率達到1。這說明IACO算法的死鎖懲罰因子起到了一定的效果。但是在算法迭代初期的時候，螞蟻存活率依舊較低。而DOACO算法通過回溯機制保證了螞蟻可以存活，路徑長度清零機制引導螞蟻調整前進方向跳離死鎖，使螞蟻存活率始終保持為1，從而有效解決死鎖問題。

圖7 3種算法螞蟻存活率變化曲線Fig.7 Comparison of ant survival rate changes of three algorithms

4.2.4綜合對比

在20×20柵格地圖的仿真環境下，本文將每種算法各仿真20次取平均值，結果如表2所示。從表2可以看出，DOACO算法在平均路徑長度、平均收斂迭代次數、平均算法收斂時間這3個性能指標上均優于ACO算法和IACO算法。算法收斂時間計算式為

表2 3種算法仿真結果Tab.2 Simulation results of three algorithms

(17)

式中T——整個程序的運行時間

Nc1——算法收斂時的迭代次數

t——算法收斂時的程序運行時間(即算法收斂時間)

本文將算法收斂時間作為衡量蟻群算法的時間尺度。如表2所示，在路徑長度方面，DOACO算法得到的路徑長度約為IACO算法的92.03%，ACO算法的91.40%，對路徑長度有一定的縮減。在收斂迭代次數方面，DOACO算法收斂所用的迭代次數約為IACO算法的25.06%，ACO算法的16.45%，收斂次數大幅度減少，同時也使得平均算法收斂時間大大縮短，充分體現了DOACO算法的優越性。

4.3 自然環境仿真實驗

自然仿真環境參照我校圖書館，實景圖如圖8a所示，圖書館面積為30 m×30 m，將整個地圖劃分為50×50柵格模型，每個柵格的實際面積為0.6 m×0.6 m。圖8b為參考實際場景建立的地圖模型，其中黑色障礙物代表圖書館中的墻壁、書架和桌子等不可行區域，紅色障礙物代表圖書館中移動的行人。移動機器人從25號柵格進入，從2 449號柵格離開。蟻群算法的參數設計如表3所示。

表3 蟻群算法參數設計Tab.3 Parameters of ant colony algorithm

圖8 圖書館實景與仿真環境Fig.8 Library real scene and simulation environment

4.3.1路徑生成

圖9為ACO算法和IACO算法在圖書館自然仿真環境下的機器人運動軌跡圖。從圖9a可以看出，ACO算法生成路徑的質量明顯較差。IACO算法生成路徑(圖9b)的質量甚至不如ACO算法。這充分說明在路徑生成方面IACO算法并不適用于圖書館這類大規模多障礙物地圖。圖10為未添加優化策略的DOACO算法和添加優化策略的DOACO算法在圖書館地圖下的機器人運動軌跡圖。從圖10a可以看出，未添加優化策略的DOACO算法生成路徑的質量明顯更好些，但是該路徑仍有進一步優化的空間。從圖10b可以看出，添加優化策略的DOACO算法生成路徑的質量最優。實驗結果所示，DOACO算法生成的路徑明顯優于ACO算法和IACO算法。

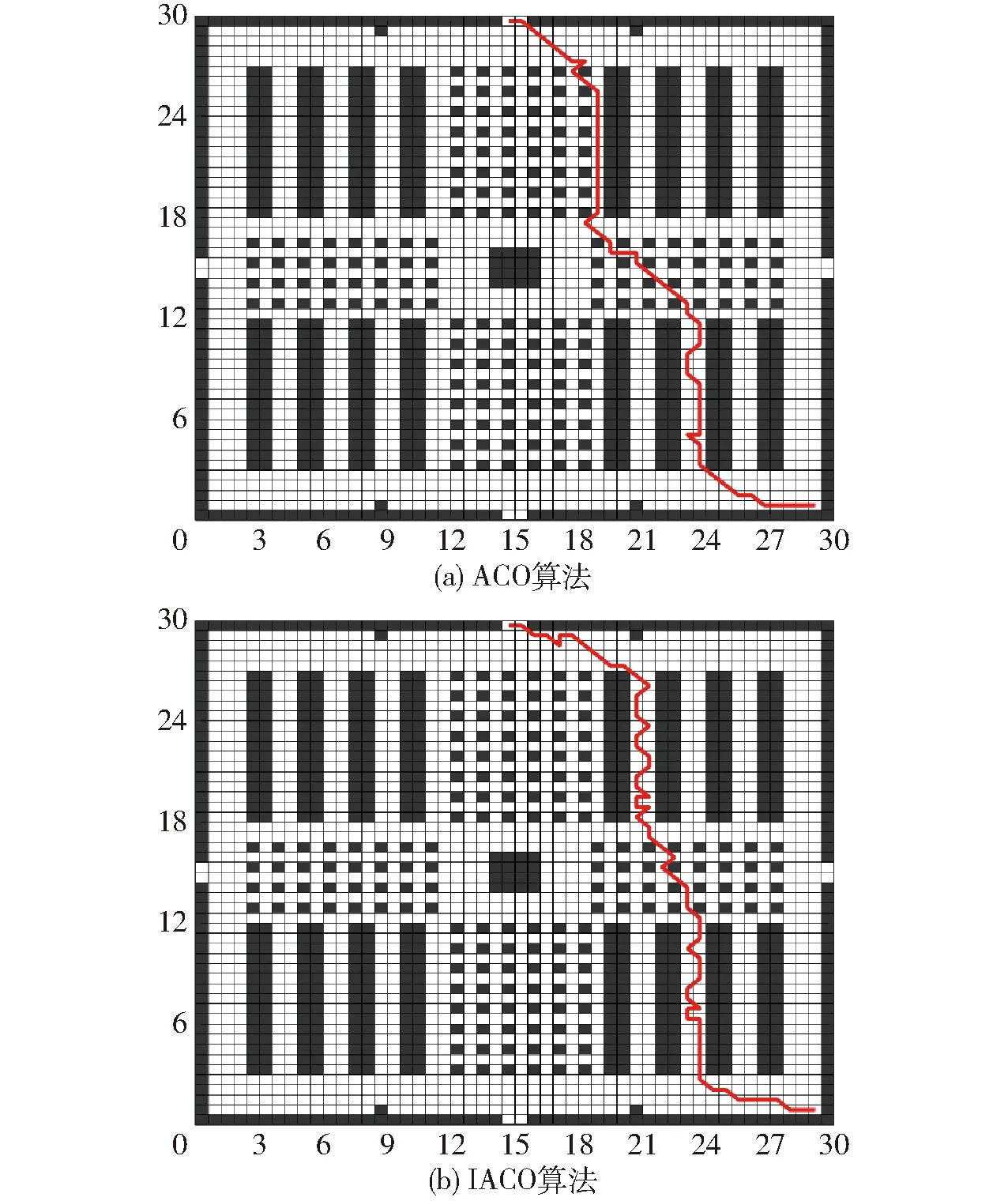
圖9 圖書館地圖下的機器人運動軌跡Fig.9 Robot motion trajectory diagram in library map

圖10 DOACO算法在圖書館地圖下的機器人運動軌跡Fig.10 Robot motion trajectory diagram of DOACO algorithm in library map

4.3.2收斂曲線分析

圖11為3種算法收斂曲線。從圖11可以看出，ACO算法在461代收斂，收斂后的最優路徑長度為39.71 m。IACO算法在43代收斂，收斂后的最優路徑長度為43.52 m。該算法主要通過改進信息素的初始分布使收斂次數減少，但同時也使算法更易陷入局部最優解，導致最優路徑長度甚至不如ACO算法。而DOACO算法在25代就已經收斂，收斂后的最優路徑長度為35.12 m。從收斂路徑長度和收斂迭代次數來看，在圖書館仿真場景中，DOACO算法比ACO算法和IACO算法性能更優，充分展現了DOACO算法中路徑優化策略以及改進的概率轉移方法的科學性。此外，從圖11中還可以發現ACO算法和IACO算法均存在數據回落現象，而DOACO算法由于采用了精英保存策略，有效避免了數據回落現象。

圖11 3種算法圖書館地圖收斂曲線對比Fig.11 Comparison of convergence curves of three algorithms in library map

4.3.3螞蟻存活率分析

3種算法在圖書館地圖下的螞蟻存活率變化曲線如圖12所示。從圖12可以看出，在388代之前，隨著迭代次數的增加，ACO算法的螞蟻存活率呈逐漸上升趨勢。在388代之后螞蟻存活率達到1并維持穩定。文獻[16]提出的IACO算法則是在245代螞蟻存活率達到1。這說明IACO算法的死鎖懲罰因子起到了一定的效果。但是在算法迭代初期時，螞蟻存活率依舊較低。而本文提出的DOACO算法通過回溯機制保證了螞蟻可以存活，路徑長度清零機制引導螞蟻調整前進方向跳離死鎖，即使在實際場景較為復雜的地圖下也依然可以保證螞蟻的存活率始終為1，從而解決死鎖問題。

圖12 3種算法圖書館地圖螞蟻存活率對比Fig.12 Comparison of ant survival rate changes of three algorithms in library map

4.3.4綜合對比

在圖書館仿真環境下，將每種算法各仿真20次取平均值，結果如表4所示。由表可知，DOACO算法在平均路徑長度、平均收斂迭代次數、平均算法收斂時間這3個性能指標上均優于ACO算法和IACO算法。在路徑長度方面，DOACO算法得到的路徑長度約為IACO算法的81.25%，ACO算法的88.71%，對路徑長度有了一定的縮減。在收斂迭代次數方面，DOACO算法收斂所用的迭代次數約為IACO算法的19.27%，ACO算法的5.23%。經實驗驗證，在自然環境仿真地圖中DOACO算法的收斂次數大幅度減少，同時也使得平均算法收斂時間大大縮短，充分體現了DOACO算法的優越性。

表4 3種算法圖書館地圖仿真結果Tab.4 Simulation results of three algorithms in library map

4.3.5動態避障

在基于圖書館地圖50×50柵格(30 m×30 m)的仿真環境中，本文在完成靜態全局路徑規劃的基礎上添加了動態障礙物。實驗共設置4個方向不同且出發時間不同的動態障礙物表示移動的行人，以此檢驗本文提出的避障策略的可行性和有效性。移動機器人動態避障的路徑軌跡如圖13所示。

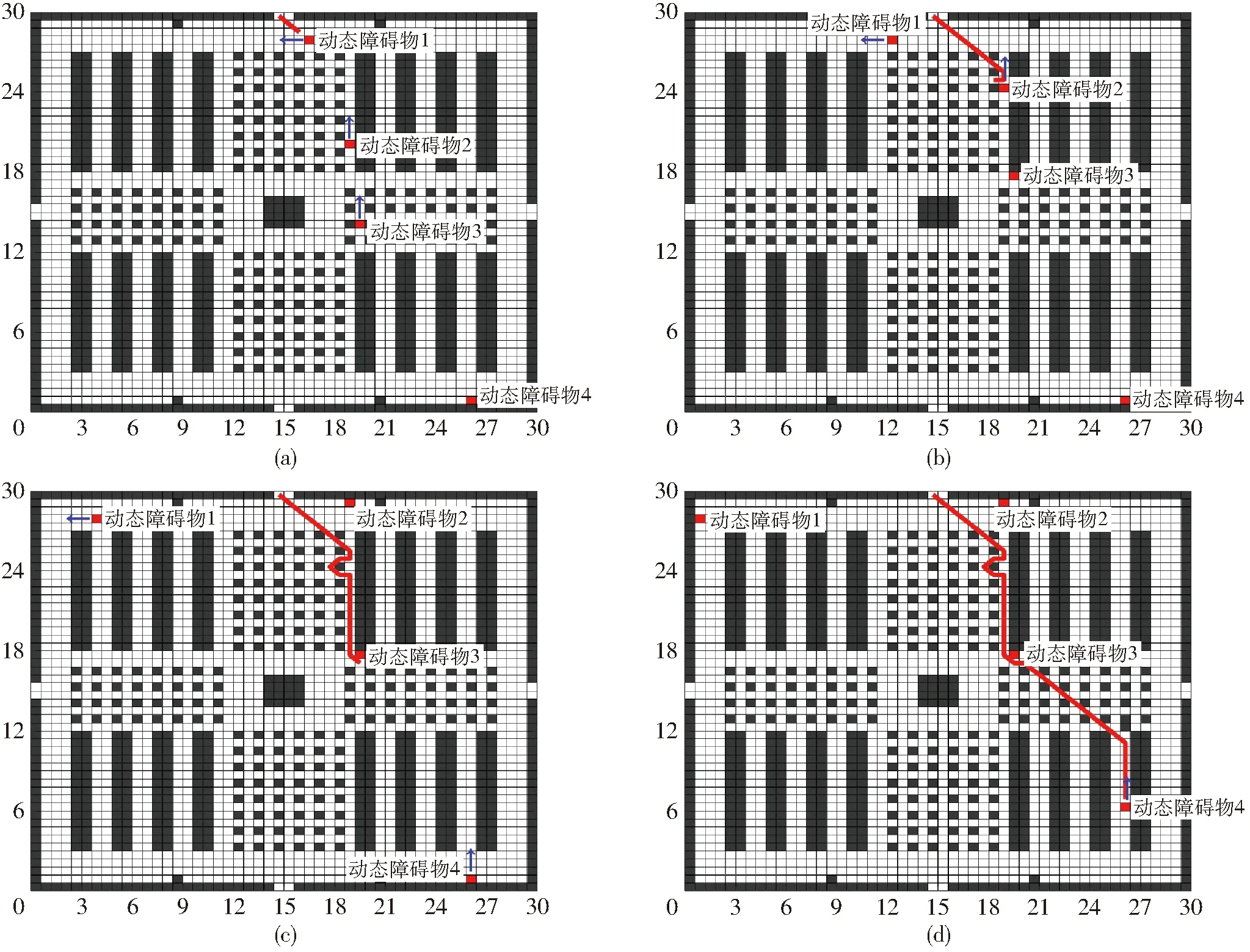
圖13 圖書館仿真環境的動態避障軌跡圖Fig.13 Dynamic obstacle avoidance trajectory diagram in library simulation environment

圖13中動態障礙物1、2、3同時出發。動態障礙物行進速度均為每次一個單位長度。動態障礙物1由181號柵格向左行進，動態障礙物2由982號柵格向上行進，動態障礙物3由1 483號柵格向上行進。根據3.1節所述的碰撞類型檢測機制，動態障礙物1在向左行進的過程中會與移動機器人發生側面碰撞。碰撞點為178號柵格。根據3.2節的避障策略，移動機器人執行等待行為。即當移動機器人預測到碰撞后，移動機器人暫時停止行進，等待動態障礙物1通過后，移動機器人再繼續前進(圖13a)。

動態障礙物2、3在移動過程中分別與移動機器人發生非接觸式正面碰撞、靜態碰撞，碰撞點分別為482號柵格和1 033號柵格。根據3.2節的避障策略，移動機器人均執行局部路徑重規劃策略。即當移動機器人預測到碰撞后，重新規劃當前路徑點到碰撞點之后的下一路徑點的路徑(圖13b、13c)。

動態障礙物4在移動機器人行進35步后開始運動，由2 444號柵格向上行進。當移動機器人行進至1 944號柵格時剛好與動態障礙物4正面相遇。根據3.1節所述的碰撞類型檢測機制可以判斷兩者為接觸式正面碰撞，故無碰撞點。根據3.2節的避障策略，移動機器人采用局部路徑重新規劃來避開障礙物。即移動機器人重新規劃1 944號柵格到2 044號柵格之間的路徑。移動機器人再按照重新規劃的局部路徑繼續前進。避障完成后，移動機器人的運動軌跡如圖13d所示。

為了測試本文提出的避障策略的實時性，仿真程序統計了4次避障所用時間。4次避障時間依次為0.000 179、0.009 581、0.000 600、0.015 197 s。而在DOACO算法的基礎上用傳統的避障策略，4次避障的避障時間依次為18.597 6、14.834 3、7.409 0、0.778 40 s。由此可見，本文提出的避障策略的實時性方面具有較好的性能。

5 結束語

提出了能夠生成高質量全局路徑的DOACO算法和適用于動態環境的避障策略，且適用于實際環境。首先，提出一種新的概率轉移函數優化算法的收斂速度，解決蟻群算法收斂速度慢的問題。其次，采用精英保存策略并提出基于碰撞檢測的路徑優化策略對收斂路徑再優化，提高收斂路徑的質量。此外，本文采用回溯機制和路徑長度清零機制相結合這一策略來解決蟻群算法的死鎖問題。最后，設計一種新的避障策略，移動機器人根據不同的碰撞類型采用不同的避障策略來躲避動態障礙物。新的避障策略可以有效地解決常規避障策略實時性不足等問題。仿真結果表明，DOACO算法在靜態和動態環境中均能生成可行有效的高質量路徑，同時也能解決基本蟻群算法存在的問題。新的避障策略可以有效地應對各種潛在的碰撞情況并且避障實時性強。