基于灰色馬爾科夫模型的電力電容器投標報價策略

羅林波，張 韜，羅嵐波，伍 娟

（1.國網湖南省電力有限公司婁底供電分公司，湖南 婁底 417000；2.國網江西省電力有限公司電力科學研究院，江西 南昌 330096）

0 引言

如今，現代企業普遍以招投標方式規范企業采購行為。隨著社會經濟的發展，招投標所涉及的經濟對象愈發大型化、復雜化，招投標行為多批次化，這給企業投標決策提出了新的挑戰[1-2]。對于企業而言，如何制定并實施正確的投標報價策略，并以此為依據得出既有合理利潤又有競爭優勢的報價，關系著企業的經濟效益乃至于企業的生存[3-4]。

國家電網有限公司評標采用綜合評估法，分技術、商務、價格三個部分分別進行量化評審，根據具體的設備標的按權重比例匯總計算最終量化評審得分[5-7]。一般來說，在電容器類商品上，各公司在技術、商務方面實力基本相當，價格得分高低是企業能否中標的關鍵。文中對國家電網有限公司2013年至2014年的電容器招投標進行分析，以中標為目的，選擇某公司作為目標公司，研究投標企業的投標報價策略。

1 基于灰色馬爾科夫模型的貨物均價預測

通過對2013 年至2014 年6 批電容器貨物的貨物數量和投標報價數據進行處理得到各批次貨物的均值，由于各批次貨物均值的變化可能呈現不規律性，故采用各類預測模型進行預測時，均需對其預測精度進行檢驗和評價。文中考慮結合馬爾科夫模型對灰色預測的殘差進行修正，從而進一步提高預測精度。

1.1 灰色預測模型

灰色預測模型一般用于對事物行為特征的發展演變趨勢進行估計預測，以及對事件發生的未來時間分布情況進行研究等。這實際上是將事物發展的“隨機過程”當作“灰色過程”研究，把“隨機變量”當作“灰變量”。

灰色模型的檢驗方法包括殘差檢驗，后驗差檢驗和關聯度檢驗，當通過全部檢驗時，才可以用來做預測，不能通過時，通過建立殘差的修正模型來提高灰色模型的精度[8-9]。

1.1.1 GM（1，1）模型求解

GM（1，1）模型是灰色模型中一種特殊的線形動態模型，兩個參數1 分別表示系統含有一個變量，即一階單變量的微分方程模型。一般只需一個時間序列，4 個以上的連續數據就可以用于求解預測的GM（1，1）模型[10]。

1.1.2 GM（1，1）建模原理與方法

為了獲取灰色預測模型所需的數據，先要對已有數據做預處理，得到累加生成序列。設原始數據序列為：

則累加生成序列為：

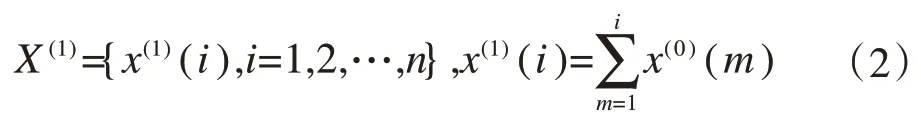
然后建立微分方程如下：

式中：X(1)為經過一次累加生成的數列；t為時間；a、u為待估參數，分別稱為發展灰數和內生控制灰數。

利用最小二乘法求參數a、u。設

解微分方程后可以得到：

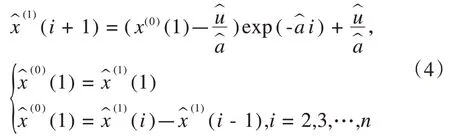
1.1.3 模型檢驗

灰色預測檢驗一般有殘差檢驗、關聯度檢驗和后驗差檢驗。

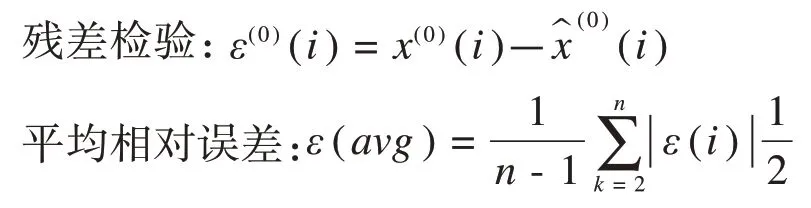
關聯度檢驗：當ρ=0.5 時，關聯度大于0.6 時認為通過關聯度檢驗，否則關聯程度不符合要求。其中關聯度的計算公式：

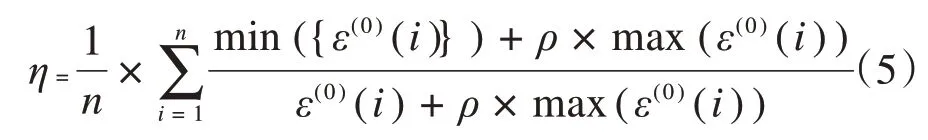
模型的后驗差檢驗依賴于小誤差概率P和后延驗差比值C，按C和P兩個指標，可以綜合評定預測模型的精度，如表1所示，其中：

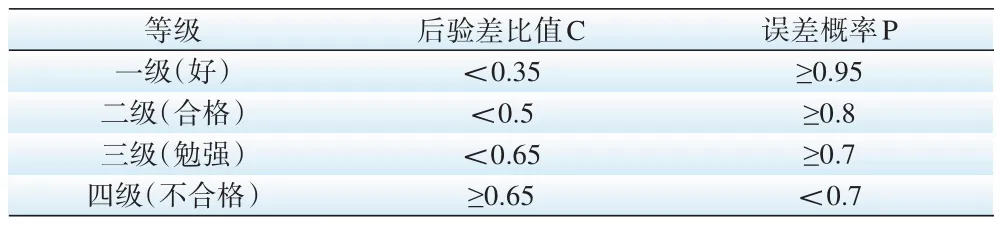
表1 后驗差比值表

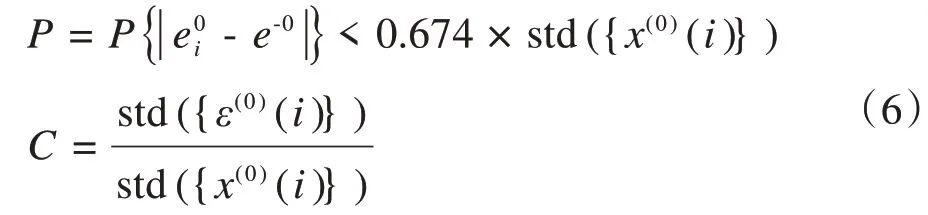
當P≤0.7 且C≥0.65 時模型不合格，其中std（·）表示標準差。

1.2 馬爾科夫預測模型

1.2.1 馬爾科夫鏈

某系統的行為特征存在一定規律性，其未來某一時間的特征只與當前時刻有關，而與過去的歷史無直接關聯，現實中普遍存在此類現象[11-13]。投標報價項目也存在這樣的特點。第一，同配置包在不同批次中報價是不同的。第二，下一批各包的報價受當前報價以及歷史批次報價的影響，其中影響最大的是當前批次報價。描述這類隨機現象的數學模型稱為馬爾科夫鏈模型[14]。

假設隨機過程序列{Xn，n≥0}，對于任意的n≥1，任一非負整數i1，j2，…in，i，j∈E，恒有P（Xn+1=j|X0=i0…，Xn-1=in-1，Xn=i）=P（Xn+1=j|Xn=i）），則稱{Xn，n≥0}為馬爾科夫鏈。如果N 為可離散集合，則稱{Xn，n≥0}為離散參數的馬爾科夫鏈。

設I為離散參數的馬爾科夫鏈的狀態空間，則稱Pij為序列從狀態i轉移到狀態j的概率，也稱條件概率；若轉移概率與實踐起點m無關，則稱此馬爾科夫鏈為非齊次馬爾科夫鏈，其狀態轉移矩陣可以表示為：

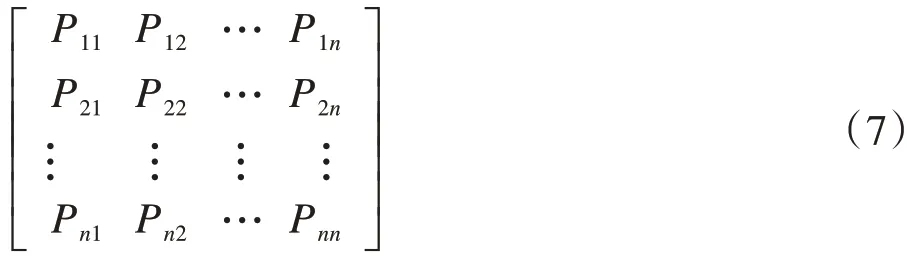
矩陣中元素非負，行和為1。

1.2.2 狀態劃分及修正

將一個具有馬爾科夫特征的非平穩隨機序列X(t)=x(0)(t)劃分為s個狀態Qi，i=1，2，…，s。任一狀態表示為Qi=[Q1i，Q2i]，其中灰元Q1i，Q2i隨時間t變化而變化，劃分狀態數s和Li，Ri可由預測值或根據具體情況而定為原始數據的均值[15]。

以ni表示處于i狀態的頻數，nij表示由狀態i經過一步轉移到狀態j的頻數，從而求出一步轉移概率矩陣：

實際應用中可能用到的多步轉移概率矩陣為Pn=Pn。

馬爾科夫鏈預測是利用每年實際值狀態變化來計算狀態轉移概率矩陣，從而得到預測值的方法，所以先把實際值按相對誤差進行劃分。{L1，L2，L3，L4}和{R1，R2，R3，R4}分別取其前四項和后四項，即得出本項目誤差的4個狀態：

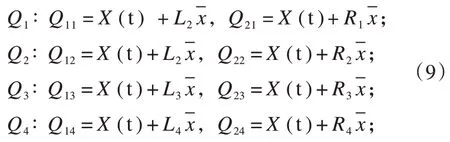
各狀態的相對誤差見表2。

表2 各狀態的相對誤差取范圍

1.3 灰色馬爾科夫模型預測貨物均價的檢驗和對比

采用灰色馬爾科夫模型對各批次貨物均價進行預測，其部分檢驗結果如表3。可見結果中原存的大量不合格預測已被修正為較好的預測值，故灰色馬爾科夫模型足以滿足貨物均價的預測需求，可用于進一步分析計算。

表3 GM（1，1）和灰色馬爾科夫模型預測結果對比

部分預測結果如圖1所示。

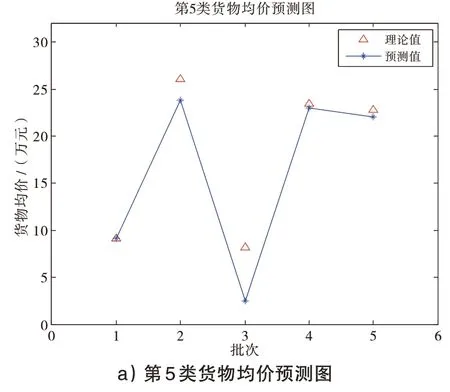
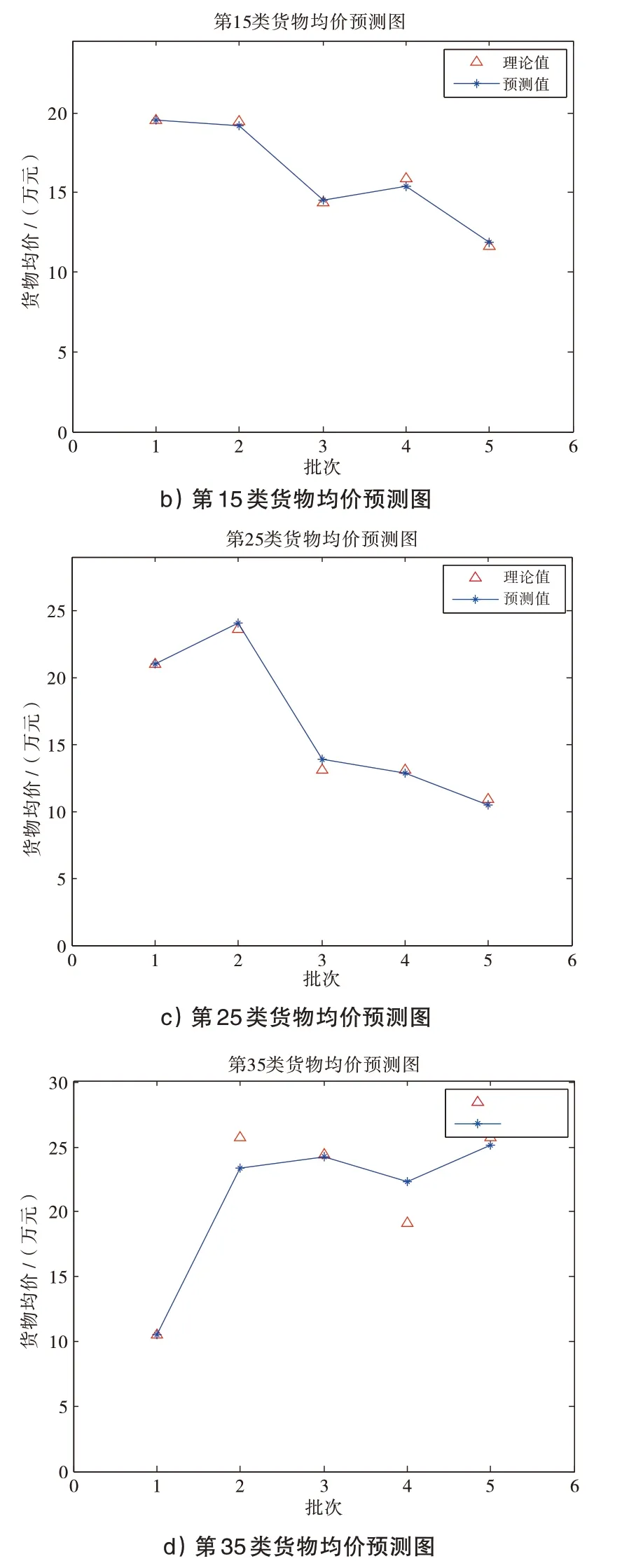
圖1 第5、15、25與35類貨物均價預測圖

1.4 預測模型的優化

定義調整系數tz2，使：

可知各批次下存在一個tz2（t），使得目標公司的中標率g1和獲得前三名的概率g2最優化。

針對前四批數據，計算得各批次下的tz2 與g1 的關系如下圖所示。

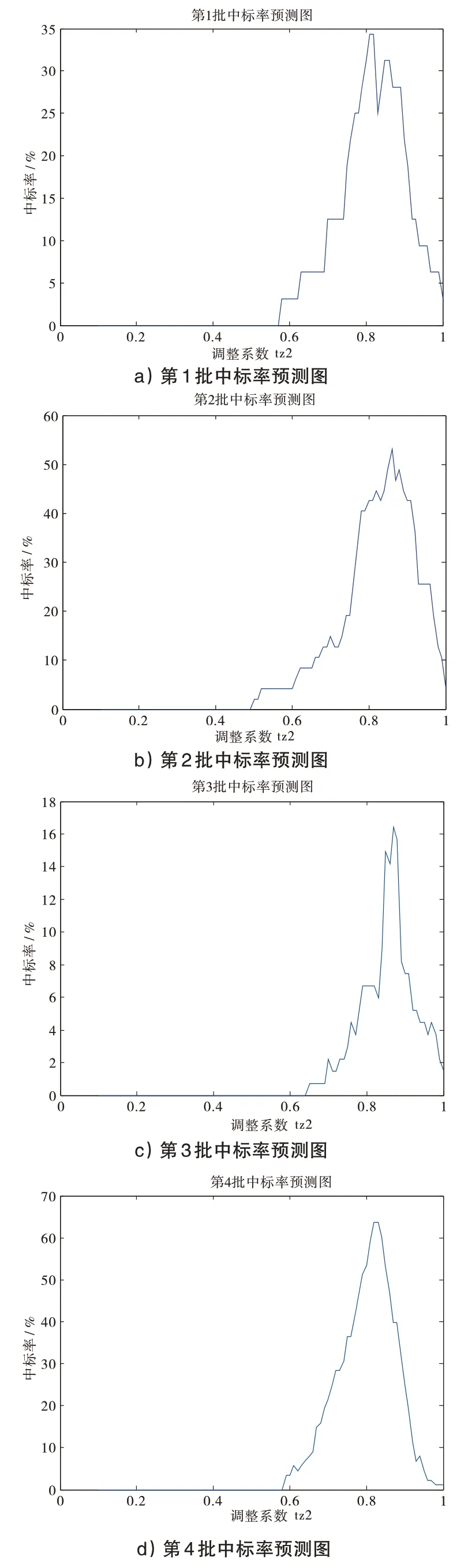
圖2 第1~4批招標調整系數與中標率關系圖

各批次下的最佳tz2值統計如表4。

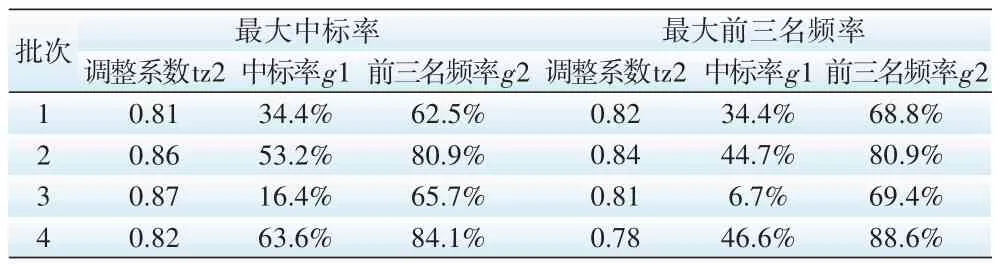
表4 g1和g2分別最佳化條件下的tz2值統計表

由表可知tz2 有較明顯的線性變換規律，故可直接采用一次函數對其進行擬合，求得tz2（5）=0.846，如圖3所示。

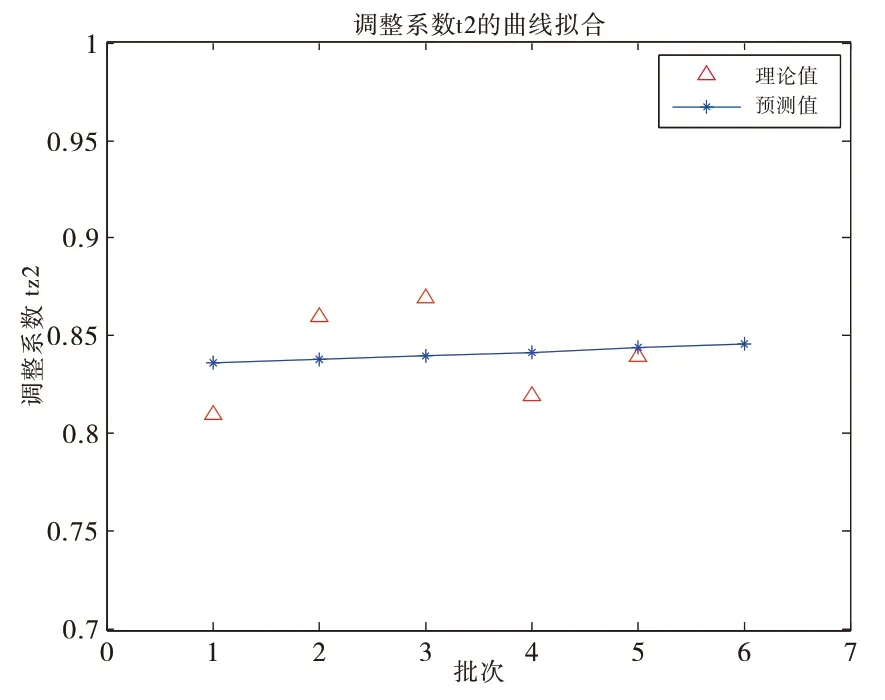
圖3 調整系數曲線擬合圖

此后可根據前4 批數據，結合調整系數tz2（5）對第5 批的投標情況進行預測，并與真實情況進行對比，從而實現該報價預測模型的檢驗。

2 預測模型的優化與檢驗

國家電網在2013 年至2015 年每年舉行6 批電容器類貨物招標，均采用綜合評標法進行招標。而文中分析 2013 年至 2014 年的 6 批招標中，主要有 17 家公司參與競標，各批次下浮比例及包數（經過數據預處理后）如表5。

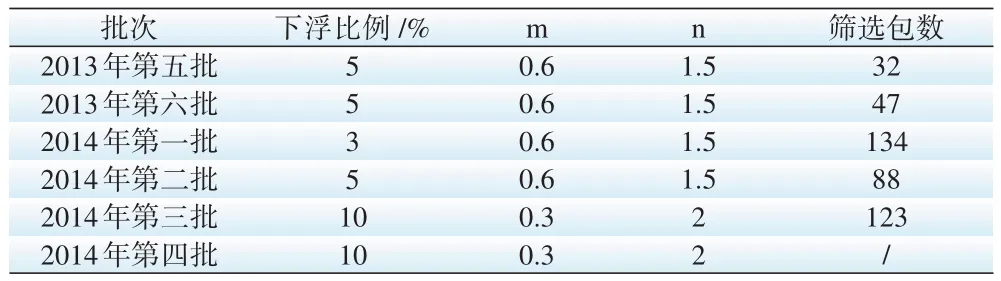
表5 各批次下浮比例及包數

通過馬爾科夫分析，得到了歷史數據中各包每類貨物的平均價格，以此為基礎建立了最優報價的數學模型，并進行了相關的改進和優化。為了驗證該模型的正確性，選擇2014 年第三批的具體情況進行分析和說明。將目標公司的實際報價與本模型的預測報價進行了對比，分別計算兩種報價的中標情況，證明了本模型的實用性，如表6。

公司招投標的最終目的是中標，由于文中假設各廠的技術、商務等實力相當，價格得分排名成為了影響中標率的單一變量。表7是將實際報價和模型預測報價所得的價格分數進行了分析，并對中標率進行比較。從表中可以得知，文中所建立的價格預測模型相對于公司的自行報價在瞄準率上有了很大的提高，價格得分第一名的頻率從1.63%大幅度提升到了20.33%，提高了將近12.5 倍；價格得分前兩名的頻率增長到41.46%，而前三名的頻率從8.13%提升至50.41%，提高了6.2倍。采用本模型所預測的價格進行投標，使得目標公司前三名的瞄準率與其余16家公司（共17家公司參與競標）前三名瞄準率之和相當。與公司的實際報價所得價格分數相比，有了質的提升。

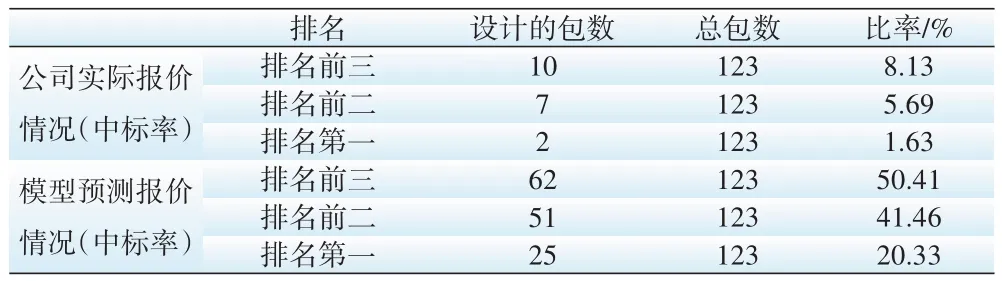
表7 模型報價和公司實際報價中標率比較

3 結語

針對國家電網有限公司電力電容器的投標問題，利用往期數據，在灰色預測基礎上進行馬爾可夫預測，既可提升灰色預測在隨機波動數據序列方面準確度，又可克服馬爾可夫預測的局限性，該模型不僅考慮了數據序列中的演變規律，而且通過狀態轉移概率矩陣的變換提取數據中的隨機響應，因此將二者結合起來將大大提高預測精度，為企業投標報價提供理論參考依據。