某作動器的正弦振動分析與試驗驗證*

喻 琴，楊 凱，段智朝，張 闖

(慶安集團有限公司航空設備研究所，陜西 西安 710077)

0 引 言

正弦振動試驗分為兩類：定頻和掃頻[1-2]。其中掃頻正弦振動試驗，分為線性掃描和對數掃描。線性掃描頻率變化是線性的，這種掃描用于細找共振頻率的試驗。對數掃描頻率變化按對數變化，低頻掃得慢而高頻掃得快。

某作動器在進行正弦振動試驗時，先進行了Z方向(如圖1所示，垂直于試驗臺臺面的方向為Z方向)線性掃描，得到其固有頻率。后進行了對數掃描，在進行對數掃描時發生了斷裂現象。筆者采用ANSYS Workbench軟件，針對某作動器進行了正弦振動分析，并基于Miner線性累計損傷理論，開展正弦振動環境下的疲勞壽命計算，認為該產品的強度較弱，提出了改進方案，后又對改進方案進行計算與試驗。

1 某作動器結構與振動條件

某作動器主要由電機、減速箱、滾珠絲杠傳動副等部分組成。固定接頭和活動接頭分別固定在試驗臺夾具上，如圖1所示。

圖1 某作動器振動安裝示意圖

在Z方向進行線性掃描試驗：頻率10～2 000 Hz、加速度2.0 g、0.5 mm幅值(峰-峰值)。得到作動器Z方向的前三階固有頻率：138、415、1 263 Hz。

接著進行對數掃描試驗：如圖2中曲線規定的振動量值。在進行了Z方向30 min振動功能后，產品左殼體零件的固定接頭耳片發生斷裂,如圖3所示。

圖2 對數掃描試驗曲線

圖3 左殼體振動試驗斷裂情況

2 模型驗證

模型驗證[3]的一般流程如圖4所示。

圖4 模型驗證流程圖

模型驗證中包括質量點、剛度以及約束的驗證。經過圖4多次驗證，得到最終的簡化模型，如圖5所示。

圖5 有限元模型

質量為5.958 kg(簡化前質量為5.95 kg)，分別在固定接頭和活動接頭圓孔處施加固定約束，其中活動接頭與關節軸承設置轉動運動副，固定接頭與關節軸承設置球運動副，如圖6(a)、(b)所示。

圖6 計算模型

對其進行模態分析，得到前8階固有頻率，見表1所列。

表1 仿真固有頻率計算結果

通過質量參與率的比較，得到Z方向前三階固有頻率為：137.08 Hz、436.21 Hz、1 258.9 Hz。由第1節知：通過正弦掃頻試驗得到作動器Z方向的前三階固有頻率：138 Hz、415 Hz、1263 Hz。Z方向的前三階仿真固有頻率與試驗固有頻率的比較見表2。

表2 仿真固有頻率與試驗固有頻率的比較

仿真固有頻率與試驗固有頻率的相關性分析時，兩者誤差在8%左右即可認為兩者相關。由表2可知，仿真固有頻率與試驗固有頻率最大誤差為0.048%，因此仿真固有頻率與試驗固有頻率吻合度很高，證明了所建有限元模型是正確的，通過模型驗證。同時給出了Z方向前三階仿真固有頻率對應的振型，如圖7所示。

圖7 Z方向前三階振型

3 正弦振動分析

對作動器展開Z方向正弦振動掃頻仿真分析[4]，并針對左殼體固定接頭耳片計算等效Mises應力，提取應力最大點的應力響應譜，如圖8所示。

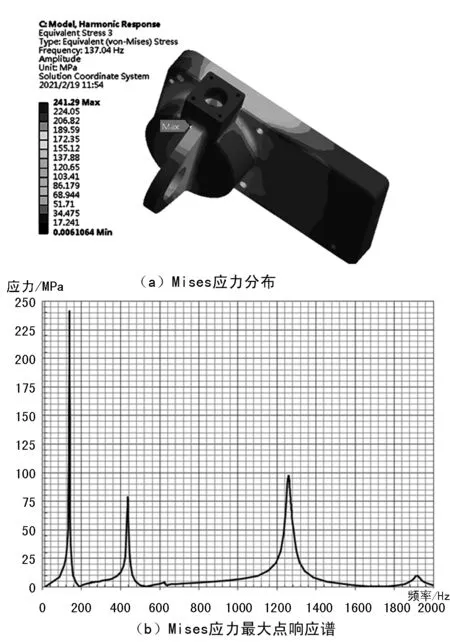
圖8 左殼體Mises應力分布及其應力最大點響應譜

經對比，左殼體應力最大點即為產品發生裂紋的位置，如圖3所示。

4 基于Miner線性累計損傷的正弦振動疲勞壽命分析

圖8所示的危險點的應力-頻率曲線，是結構在正弦振動條件下的應力隨時間變化的頻域描述，因此基于該曲線，結合Miner線性累計損傷理論，可以計算其疲勞壽命。

正弦振動過程中，振動時間、頻率和掃描率的關系為:

(1)

上式中R為正弦振動掃描率。

上式等號兩側對f求導數，則有:

(2)

寫成離散形式，可得:

(3)

(4)

進一步，可計算Ni如下:

(5)

在多級不同應力幅值σi作用下,各級應力對應的Ni描述如下：

(6)

根據式(2)可得:

(7)

將上式寫成離散形式:

(8)

上式中T為正弦振動持續時間，t為單次掃頻所需時間。

壽命計算公式為：

(9)

根據Miner線性損傷累計理論，當D<1時，可以認為構件不會發生疲勞破壞，在工程中通常取安全系數為10，即D<0.1，L≥10時，認為構件不會發生疲勞破壞[5]。

基于上一節獲得的左殼體固定接頭耳片Mises應力最大值點的頻率-應力曲線(圖8)，結合上述理論公式，可以計算左殼體Z方向30 min振動功能正弦振動疲勞壽命，見表3。結果表明左殼體不滿足正弦振動疲勞壽命要求，與正弦振動試驗結果相符，左殼體耳片發生了斷裂，如圖3所示。

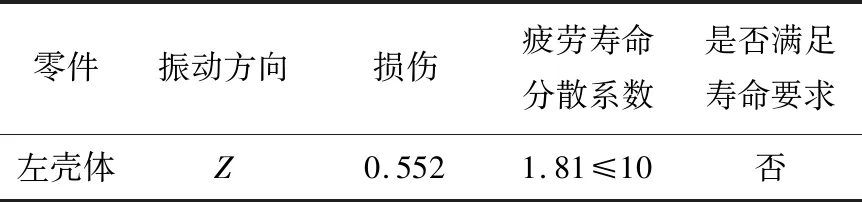
表3 正弦振動疲勞壽命校核

5 改進方案

將左殼體材料由鋁合金2618A-F更改為沉淀硬化不銹鋼15-5PH，左殼體固定接頭耳片的厚度由7.4 mm增加至13 mm，提高左殼體固定接頭耳片的強度。殼體耳片改進后振動仿真情況如圖9所示。左殼體Z方向振動疲勞壽命分散系數為9.16E+02>10，殼體振動壽命滿足要求。

圖9 改進后左殼體Mises應力分布及其應力最大點響應譜

在改進左殼體的同時把振動試驗工裝也進行了改進，如圖10所示。重新進行試驗，正弦振動試驗合格，說明采取的改進措施切實有效。

6 結 論

針對某作動器的固定接頭耳片在正弦振動試驗中發生斷裂，文中開展了正弦振動疲勞分析，主要結論如下。

(1) 建立了作動器結構的有限元分析模型，基于正弦掃頻試驗獲得Z方向前3階的固有頻率，對模型進行了修正，修正后的分析結果與試驗數據的一致性較好。

(2) 根據正弦疲勞壽命計算公式，結合正弦分析獲得危險點應力—頻率曲線，對耳片進行了疲勞壽命預測，結果表明，左殼體不滿足正弦振動疲勞壽命要求，且最危險位置與試驗結果相符。

(3) 根據仿真計算結果，對材料和尺寸進行了改進，提高了左殼體固定接頭耳片的強度，其Z方向振動疲勞壽命分散系數為9.16E+02>10，重新進行試驗后，正弦振動試驗合格，說明采取的改進措施切實有效。