技術積累提高了區域創新數量還是創新質量

俞立平

(浙江工商大學 統計與數學學院，浙江 杭州 310018)

0 引言

隨著中國經濟發展由追求數量轉向追求質量，創新質量越來越受到重視。創新質量是企業全方位各領域質量的綜合體現，包括產品與服務質量、運作過程質量以及企業管理質量，可通過績效、數量、有效性、可靠性、特征、時間性、客戶價值、成本、創新程度、復雜性等指標體現[1]。進入21世紀以來，隨著創新驅動發展戰略的實施，我國創新水平提升很快。據國家統計局公布的數據顯示，目前我國發明專利申請量和研發人員數量已經位列世界第一，科技論文數量和研發經費數量位列世界第二，但我國創新質量仍然不高。由世界知識產權組織等發布的《2020年全球創新指數報告》顯示，我國創新質量位列全球第16位，在基礎研究、關鍵技術研究以及吸引全球創新資源等方面還存在一定差距。

技術積累對企業創新無疑具有十分重要的意義。技術積累是指企業技術知識、技術能力的增加與遞進，包括研究與開發能力、生產能力、工藝能力等，是企業已積累的技術存量[2]。豐富的技術積累不僅有利于企業開發新產品，而且有助于提高生產與工藝水平，使得新產品能夠快速量產，從而獲得較強競爭優勢。技術積累是企業創新的基礎，而企業創新反映了技術積累水平。因此，研究技術積累與創新數量、創新質量的關系具有重要意義。只有少量研究關注技術積累與創新關系，沒有進一步從創新數量、創新質量角度作深入分析，相關問題包括：①技術積累與創新數量/創新質量的作用機制；②技術積累與創新數量/創新質量的線性關系；③技術積累對創新數量/創新質量的作用特征、規律以及存在問題；④創新數量/創新質量對技術積累的反饋機制與影響效應等。開展上述問題研究不僅有利于推進技術創新機制與創新質量理論建設，而且對于加強技術積累、提高創新質量、提升企業創新效率具有重要意義。本文將以高技術產業為例，從宏觀區域視角研究技術積累與創新數量/創新質量的關系，從而為高技術產業創新政策制定提供借鑒。

1 文獻綜述

關于創新質量的界定與測度，Lanjouw等[3]、Teemu等[4]認為，創新質量既包含創新的技術價值，也包含由此帶來的商業價值；姜博、馬勝利等[5]提出，高技術產業創新質量包括創新生成質量、創新應用質量、創新擴散質量和創新轉化質量等；Guellec等[6]指出，授權專利擁有比未被授權專利更高的質量；Rubashkina等[7]、Johnstone等[8]認為，應基于專利信息衡量創新質量，其中，專利引用數是衡量創新質量的一個較好指標；Schettino等[9]采用主成分分析法提煉出同族專利規模、專利申請寬度、專利前向引用和后向引用4個指標，用以衡量創新質量；閆緒嫻、曾強[10]指出，研究創新質量不應僅從微觀企業層面著手，還應該關注宏觀區域與產業層面。

關于創新質量的影響因素，李長英、趙忠濤[11]認為，技術多樣化對創新數量與創新質量具有倒U型影響，不相關技術多樣化對創新數量與創新質量具有正向影響；李揚、樊霞等[12]研究了產學研合作對科學與技術研發質量的影響，發現基于理論的產學研合作較弱但創新質量更高，基于實踐的產學研合作較強但創新質量較低；陳戰光、李廣威等[13]研究發現，研發投入能夠顯著提升企業創新質量，知識產權保護與企業創新質量呈顯著的倒U型關系；賓厚、馬全成等[14]發現，產學研協同創新中的合作開發、人才輸送模式與技術創新質量呈正相關關系，技術轉讓模式與產業技術創新質量關系不顯著；黃倩、宋鵬等[15]研究了人民幣匯率、中間品進口對出口產品質量的影響；李曉龍、冉光和[16]研究了數字金融對創新質量的影響；袁勝軍、俞立平等[17]研究了創新政策對創新質量的影響，發現創新政策以提升創新數量為主，對創新質量的影響不顯著，我國創新政策必須從重視創新數量轉向重視創新質量。

關于技術積累的界定與內涵，Arrow[18]開創了技術積累研究，提出技術進步與技術積累既相互聯系又有所區別，技術進步是技術積累的結果，但技術積累并不一定帶來技術進步；Hayek[19]指出，企業知識來自企業內部，并通過日常經營積累或研發產生新知識；宋寶香、彭紀生等[20]認為，技術能力是企業在持續的技術學習與變革中進行產品生產或服務提供的累積性知識、技能與經驗，是企業持續進行技術積累的結果；邢麗娜[21]提出，技術積累是一個知識吸收與應用過程，是企業技術能力形成的關鍵；曹勇、趙莉等[22]認為，技術積累不僅是企業知識性資源，也是研發投入的具體體現，能反映企業研發支出范圍，是對技術創新過程的一種投入；滕璐璐、王傳磊[23]將技術積累劃分為狹義技術積累、組織積累和文化積累3個層面。

關于技術積累的測度，Porter等[24]以專利申請授權量作為核心變量，通過永續盤存法測度技術積累；楊菲、安立仁等[25]采用因子分析法，從自主積累、開放式積累兩個角度綜合評價我國區域技術積累能力，分析地區技術積累能力結構；孫菁、王京等[26]選取無形資產中的專利、專有技術或非專有技術以及軟件等凈值反映技術積累；岳宇君、孟渺[27]采用發明專利申請數作為技術積累的替代變量。

關于技術積累現狀及影響因素，萬廣華、范蓓蕾等[28]認為，由于地理、資源稟賦和歷史等因素，我國東中西部的技術創新能力始終存在無法忽視的差距；Sydow等[29]研究發現，技術積累過程既受到成本約束，也受組織剛性和技術路徑影響；Hobday[30]研究了代工企業通過技術轉移實現技術積累的機制，包括來自客戶的支持、員工培訓、接入國際市場、追趕國際技術前沿等。

關于技術積累與創新的關系，Cohen[31]認為，技術積累是企業形成消化吸收能力的基礎，更是二次創新的關鍵；Oded[32]研究發現，隨著技術積累水平提升，研發投入產出的邊際收益降低，技術積累水平在研發投入與創新績效間發揮負向調節作用；郭秀強、孫延明[33]研究了研發投入、技術積累與高新技術企業市場績效之間的關系機理；尚濤、鄭良海[34]研究發現，在技術轉移后期，隨著企業技術能力增強，跨國公司通過市場勢力與資源需求控制阻止代工企業技術升級，表現為對技術升級傾向、技術升級投入、技術轉移內容的抑制與控制。

從現有研究看，關于創新質量的界定既有廣義的，也有狹義的，主要從微觀企業層面界定創新質量，從產業層面開展的研究并不多，且關于創新質量的測度方法也較成熟。關于創新質量的影響因素，現有研究涉及技術多樣化、產學研合作、研發投入、協同創新、創新文化、顧客創新、創新政策等。關于技術積累的界定，學術界并沒有太大爭議，由于技術能力與技術積累密切相關，因此兩者演化趨同。有關技術積累的實證研究不多，其影響因素研究包括積累模式、成本、組織剛性、技術路徑、技術轉移等。綜上所述，本文將從以下方面作深入分析：

第一，在創新與技術積累關系的研究中，只有少量文獻涉及創新數量，缺乏對創新質量的研究。因此，本文針對技術積累對創新質量的影響機制作進一步探究。

第二，從實證研究角度，有必要厘清技術積累與創新數量/創新質量的關系，包括線性關系和非線性關系，從而掌握技術積累對創新數量/創新質量的作用特征、作用規律以及存在問題。

第三，關于技術積累對創新數量/創新質量的反饋機制以及反饋效應缺乏研究，有必要作深入分析。

本文以高技術產業為例，在分析技術積累對創新數量/創新質量影響的基礎上，綜合采用聯立方程模型、面板門檻模型、向量自回歸模型開展研究。本文創新之處是開創了技術積累對創新質量影響的新研究領域，研究方法也體現了綜合性、系統性和穩健性，對于提高我國創新質量具有重要借鑒意義。

2 理論分析與研究方法

2.1 理論分析

2.1.1 技術積累分類

本文將技術積累總體上分為生產技術積累與研發技術積累兩類。生產技術積累包括生產工藝與生產技術積累、檢測與配套技術積累兩個方面，這是企業實現規模生產的前提條件。研發技術積累包括傳統技術積累、相關技術積累和新興技術積累三類。其中，傳統技術積累是采用傳統技術路徑通過不斷優化、升級形成的技術積累；相關技術積累是與傳統技術創新相關的一些技術領域的積累，如創新拓展、創新集成等；新興技術積累是采用全新知識或技術進行研發而產生的相關技術積累。

知識積累是技術積累的重要基礎。通常情況下，傳統知識是傳統技術積累以及相關技術積累的基礎，比如傳統的化學感光知識積累催生了膠片相機技術積累；而前沿知識是新興技術積累的基礎，比如電子感光理論的出現催生了數碼相機的相關技術積累。

2.1.2 技術積累與創新數量

創新數量是一個總量概念，由于絕大多數創新以傳統創新為主，因此技術積累與創新數量關系的研究應重點從傳統創新角度展開。

技術積累與創新數量關系包括以下方面：第一，傳統技術積累對創新數量的作用機制包括完善效應、拓展效應。其中，完善效應是指沿著原有技術路徑不斷完善、優化現有產品設計；拓展效應是在現有技術不變的情況下，通過實用新型或外觀設計進行創新。第二，基于相關技術積累進行集成創新，從而增加創新數量。第三，基于生產技術積累進行工藝改進，提高產品質量、擴大產能、降低廢品率等，進而增加創新數量。

需要說明的是，創新數量對技術積累具有反饋作用，如技術積累較多，會帶來創新數量增加，實現較高收益，進而促進企業進一步加大技術積累投入，形成良性循環。

2.1.3 技術積累與創新質量

關于創新質量與創新類型的關系，Schumpeter[35]提出創新的5種類型，分別是開發新產品、采用新生產方式、開辟新市場、發現新原材料或半成品來源、形成新工業組織。從技術創新角度，新產品、新生產方式、新原材料或半成品來源均與重大創新或創新質量相關。

技術積累與創新質量的關系包括：第一，新興技術積累具有兩個作用，即提供新產品與新材料半成品來源，這無疑對創新質量具有重大意義。第二，重大相關技術積累會產生重大集成創新，如載人航天、高鐵技術等，它們同樣屬于創新產生新產品的范疇，也是創新質量的重要組成部分。第三，重大生產技術積累會催生新生產方式，這同樣是創新質量的體現。

同時，創新質量對技術積累也具有反饋作用，如良好的技術積累會帶來創新質量提高，進而帶來高額回報，促進企業進一步加大新興技術積累、重大相關技術積累、重大生產技術積累等投入，形成良性循環。

2.2 研究框架

本文研究框架如圖1所示。Griliches[36]在經典Cobb-Douglus生產函數的基礎上，提出以科研成果作為產出、研發經費作為投入建立知識生產函數，而后Jaffe[37]在投入變量中引入研發人員變量，這就是著名的Griliches-Jaffe知識生產函數。本文借鑒上述理論模型，將科技創新成果分為創新數量、創新質量兩個維度。鑒于研發投入、技術積累與創新數量/創新質量之間存在復雜的互動關系，并且創新數量與創新質量之間也存在互動關系，因此本文首先采用聯立方程模型研究技術積累與創新數量、創新質量之間的關系，從而得出它們之間的平均彈性系數，這是一種線性關系模型。然后，為了進一步刻畫技術積累與創新數量/創新質量之間的關系特征、作用規律和存在問題，繼續采用面板門檻模型開展研究，這是一種非線性關系模型。最后，為了研究技術積累與創新數量/創新質量之間的互動關系，進一步采用貝葉斯向量自回歸模型開展研究，重點從脈沖響應函數角度分析變量間的互動關系，以彌補線性關系與非線性關系靜態研究的不足。

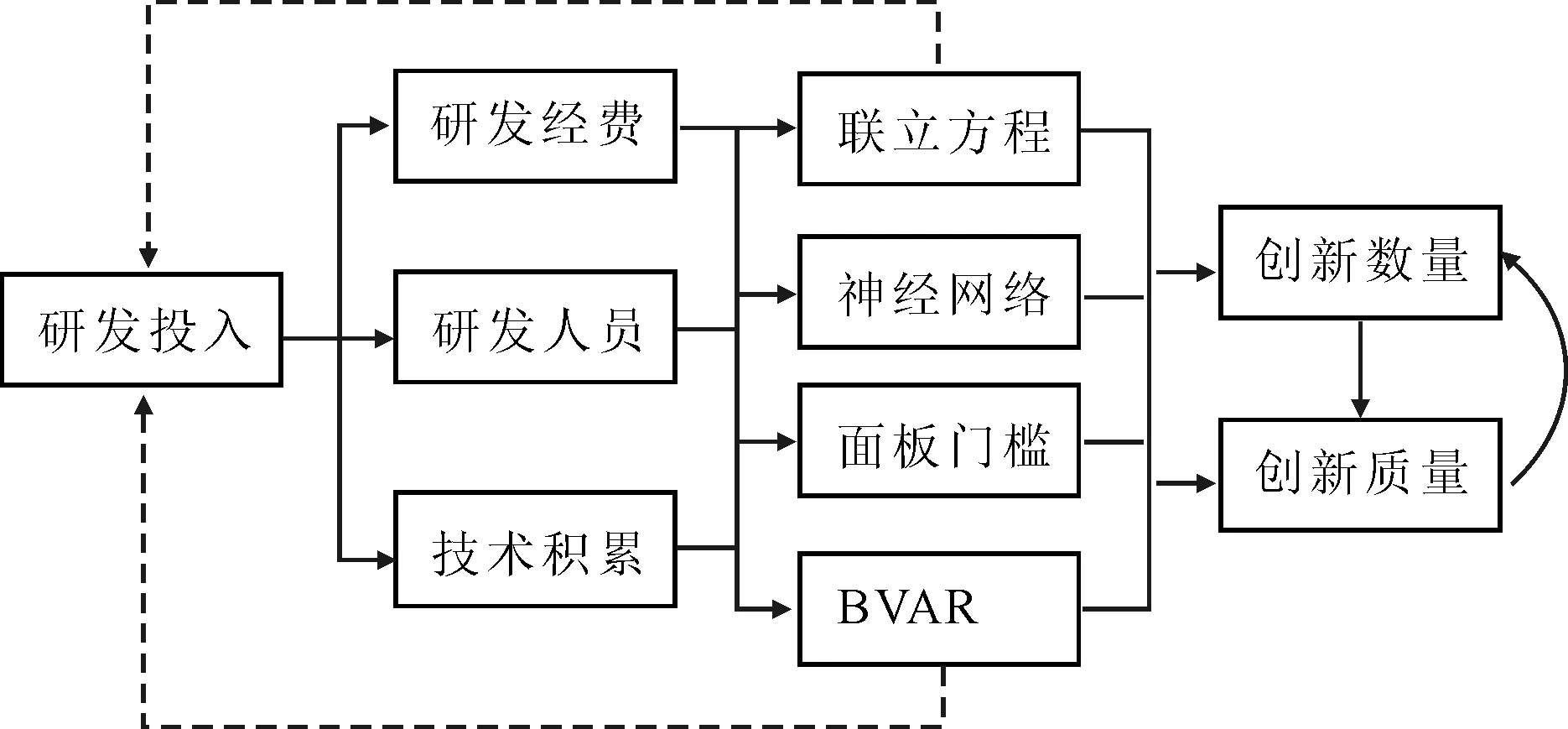
圖1 研究框架Fig.1 Research framework

2.3 研究方法

2.3.1 面板聯立方程模型

采用聯立方程模型估計技術積累與創新數量/創新質量、研發經費、研發人員等變量之間的復雜關系，聯立方程模型如下：

式中，Y1為創新數量，Y2為創新質量，K為研發經費、L為研發人員，T為技術積累。cij表示回歸系數，其中,i表示方程序號，j代表變量序號，i,j=1,2,3,4,5。

方程(1)為創新數量方程，影響因素包括研發經費、研發人員、技術積累、創新質量。考慮到相關要素對創新數量的作用存在滯后性，因此研發經費、研發人員、技術積累3個變量均滯后1期，但對創新質量沒有設置滯后期。

方程(2)為創新質量方程，影響因素包括研發經費、研發人員、技術積累、創新數量。同樣，考慮到時間滯后性，研發經費、研發人員、技術積累3個變量均滯后1期，但對創新數量沒有設置滯后期。

方程(3)為研發經費影響因素方程，包括研發人員、創新數量、創新質量等變量，所有變量均滯后1期。方程(3)沒有引入技術積累，主要原因是技術積累對研發經費投入的影響既有正向效應，也有負向效應，疊加后總效應較弱。

方程(4)為研發人員影響因素方程，包括研發經費、創新數量、創新質量等變量，所有變量均滯后1期。技術積累對研發人員的影響總體較弱，因此沒有引入。

方程(5)為技術積累影響因素方程，包括研發經費、研發人員、創新數量、創新質量等變量，所有變量均滯后1期。

以上方程均進行取對數處理，主要原因有兩個：①取對數后所有回歸系數均變成彈性系數，且不同方程的回歸系數可以直接比較，變量計量單位對回歸結果無影響；②可以有效降低異方差影響，使回歸精度更高。

2.3.2 面板門檻回歸模型

為了研究技術積累與創新數量、創新質量的非線性關系，需要采用面板門檻回歸模型[39]進行分析。該模型中，因變量包括創新數量、創新質量，核心變量為技術積累，門檻變量包括創新數量、創新質量、研發經費、研發人員、技術積累等，理論上共包括10個模型。對于創新數量而言，通過識別技術積累對創新數量的貢獻可以分析創新數量門檻、技術積累自身門檻、創新質量門檻、研發經費門檻、研發人員門檻；對于創新質量而言，技術積累對創新質量的貢獻可以研究創新質量門檻、技術積累自身門檻、創新數量門檻、研發經費門檻、研發人員門檻。以技術積累對創新質量貢獻的研發經費門檻為例，建立如下模型：

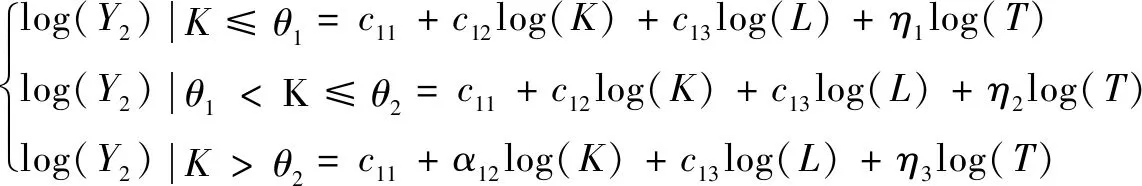
(6)

式(6)考慮了雙門檻情形，即存在2個研發經費門檻θ1和θ2，使得技術積累對創新質量的彈性出現顯著差異，當K≤θ1時，T對創新質量的彈性為η1；當θ1θ2時，T對創新質量的彈性為η3。

具體門檻數量需要通過門檻效應檢驗獲得，并綜合考慮研究問題、數據量等諸多因素。

2.3.3 貝葉斯向量自回歸模型

為了研究技術積累與創新數量、創新質量的互動關系，采用貝葉斯向量自回歸模型進行動態分析。貝葉斯向量自回歸模型(Bayesian Vector Autoregressions，BVAR)是Litterman[39]將貝葉斯推斷理論與傳統VAR模型高度融合的結晶，其最大優勢是通過對少數超級變量的估計，彌補VAR模型對眾多參數估計的不足，從而最大限度地節省自由度，提高模型估計精度與預測效果。

2.3.4 BP人工神經網絡

為了對技術積累與創新數量、創新質量的回歸結果進行穩健性檢驗，借鑒BP人工神經網絡模型，將研發經費、研發人員、技術積累作為投入變量，創新數量、創新質量作為產出變量，建立BP人工神經網絡機器學習模型，并對其進行訓練，從而得到技術積累、研發經費、研發人員權重。這本質上與回歸系數含義接近，通過對比分析實現穩健性檢驗。雖然這種穩健性檢驗屬于方法層面的，但是在研究計量模型不唯一的情況下具有重大意義。

BP神經網絡模型能夠模擬人類大腦神經網絡基本特征與工作原理，同時，可進行并行計算和分布式信息處理[40]。常見的BP人工神經網絡由輸入層、隱含層、輸出層組成，其中，隱含層可以是多個。BP人工神經網絡的學習原理是通過不斷調整網絡連接權重，使得網絡總體誤差最小化。最小誤差的學習閾值可以通過人工設定，目前技術成熟，已經廣泛應用在管理學、心理學、人工智能等諸多領域。

3 研究數據與實證結果

3.1 研究數據

本文以高技術產業為例展開研究。由于創新數量側重于總量，且創新數量包括不同水平創新，因此借鑒蔡紹洪、俞立平等的研究，采用新產品銷售收入表示。創新質量的測度方法較多[6-8]，有的采用發明專利數，有的采用指標體系測度，本文基于宏觀產業層面開展研究，因此采用發明專利授權數占申請數的比重表示。技術積累是企業長期努力的結果，是存量概念，因此本文采用有效發明專利數表示。研發經費采用研發經費內部支出表示，研發人員采用研發人員折合全時當量表示，這也是學界的通行做法。

本文所有數據均來自《中國高技術產業統計年鑒》，由于發明專利授權數與申請數于2010年才開始公布，因此本文數據范圍為2010-2019年。另外，西藏、新疆、寧夏、青海數據缺失較多，因此未納入統計與研究，實際取樣為27個地區的省際面板數據。變量描述性統計結果如表1所示。

表1 變量描述性統計結果Tab.1 Variable descriptive statistics

3.2 聯立方程估計結果

基于式(1)～式(5)的聯立方程模型進行估計，估計方法采用二階段最小二乘法，工具變量借鑒Blundell的研究，采用各變量一階滯后項表示，估計結果如表2所示。5個方程的擬合優度分別為0.869、0.204、0.937、0.927、0.899，除創新質量方程擬合度偏低外，其它方程擬合度總體較高，模型總體擬合效果較好。創新質量方程擬合度偏低的原因是，目前我國高技術產業創新質量不高，加上一些影響因素難以量化。

表2 聯立方程估計結果Tab.2 Estimation results of simultaneous equation model

式(1)中，研發經費的彈性系數最高，為0.571，其次是技術積累，彈性系數為0.287，第三是創新質量，彈性系數為-0.789，三者均通過統計性檢驗。研發人員的彈性系數為0.233，沒有通過統計檢驗。創新質量對創新數量的影響系數為負，說明要提高創新數量，必須犧牲創新質量，兩者協調性不佳。

式(2)中，研發經費的彈性系數最高，為0.121，其次是技術積累，彈性系數為0.106，第三是創新數量，彈性系數為-0.077，第四是研發人員，彈性系數為-0.156，以上均通過統計性檢驗。創新數量的彈性系數為負，說明要提高創新質量，必須犧牲創新數量，兩者不協調。研發人員的彈性系數為負數，原因有兩方面，一方面是從提高創新質量角度考慮，我國研發人員素質有待提高；另一方面是目前的變量無論是采用研發人員折合全時當量還是研發人員數量，均無法反映不同水平研發人員的貢獻，且數據獲取有限。

式(3)中，研發人員的彈性系數最大，為0.680，其次是創新數量，彈性系數為0.288，第三是創新質量，彈性系數為0.268，三者均通過統計性檢驗，說明創新數量、創新質量提升對研發經費均具有較好的反饋作用。

式(4)中，研發經費的彈性系數最大，為0.709，其次是創新數量，彈性系數為0.153，第三是創新質量，彈性系數為-0.560，三者均通過統計性檢驗。這是因為創新數量由于重視量的擴張，因此對研發人員具有較好的正向反饋，而創新質量提升較困難，需要以科研精英和團隊作為支撐，因此對一般意義的研發人員折合全時當量難以產生正向反饋。此外，由于研究數據所限，難以區分不同研發人員的貢獻，這也是導致創新質量對研發人員難以產生正向反饋的一個重要原因。

式(5)中，創新質量的彈性系數最大，為0.831，其次是研發經費，彈性系數為0.793，第三是創新數量，彈性系數為0.217，三者均通過統計性檢驗。研發人員的彈性系數為-0.062，沒有通過統計性檢驗。從技術積累角度，創新質量的反饋作用比創新數量顯著，這是值得肯定的。

聯立方程可視化結果如圖2所示，圖中實線表示正相關，虛線表示負相關，箭頭表示變量影響方向，線寬表示彈性大小。圖中可以明顯看出，創新數量提升有較好的方法，總體線條較寬，而創新質量提升尚缺乏有效手段，總體線條較窄。技術積累對創新數量的貢獻大于創新質量，并且創新質量的反饋對技術積累的影響更顯著。

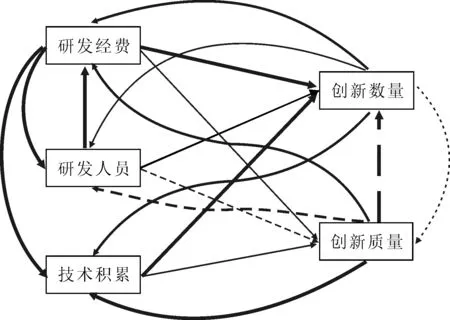
圖2 聯立方程可視化結果Fig.2 Visualization results of simultaneous equations

3.3 面板門檻回歸模型估計結果

3.3.1 技術積累對創新數量、創新質量的技術積累門檻

分別以創新數量、創新質量作為因變量，研發經費、研發人員作為控制變量，技術積累作為核心變量，同時，將技術積累作為門檻變量，采用面板門檻回歸模型進行回歸。為了便于比較，通常采用雙門檻模型進行估計，除非門檻檢驗未通過，否則采用雙門檻回歸結果。實證結果如表3所示。

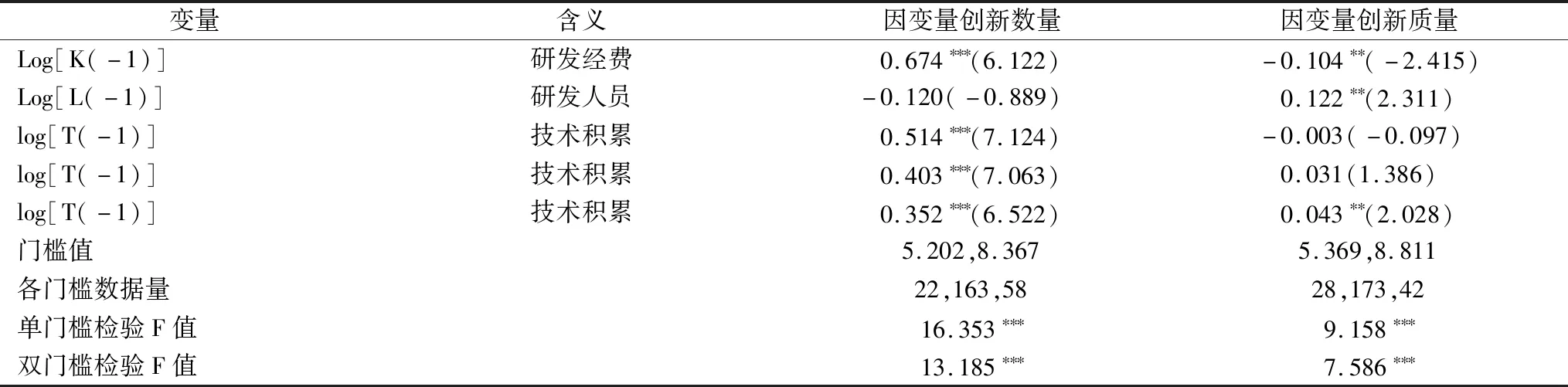
表3 技術積累自身的門檻效應估計結果Tab.3 Estimation results of technology accumulation′s threshhold effect

當因變量是創新數量時，技術積累存在兩個門檻，對應值分別為5.208、8.367，將技術積累分為低水平、中等水平、高水平三類，數量分別為22、163、58個，以技術積累中等水平地區為主。技術積累對創新數量的彈性系數分別為0.514、0.403、0.352，均通過統計性檢驗，說明隨著技術水平提高，其對創新數量貢獻的彈性總體是下降的，呈規模報酬遞減特征。

當因變量是創新質量時，技術積累同樣存在兩個門檻，其對應值分別為5.369、8.811，將技術積累分為低水平、中等水平、高水平3類，數量分別為28、173、42個，同樣以技術積累中等水平地區為主。技術積累對創新數量的彈性系數分別為-0.003、0.031、0.043，但只有后者通過統計性檢驗，說明只有當技術積累水平很高時，才能有效提高創新質量。

3.3.2 技術積累對創新數量、創新質量的創新數量門檻

分別以創新數量、創新質量作為因變量，研發經費、研發人員作為控制變量，技術積累作為核心變量，創新數量作為門檻變量，采用面板門檻回歸模型進行回歸。實證結果如表4所示。

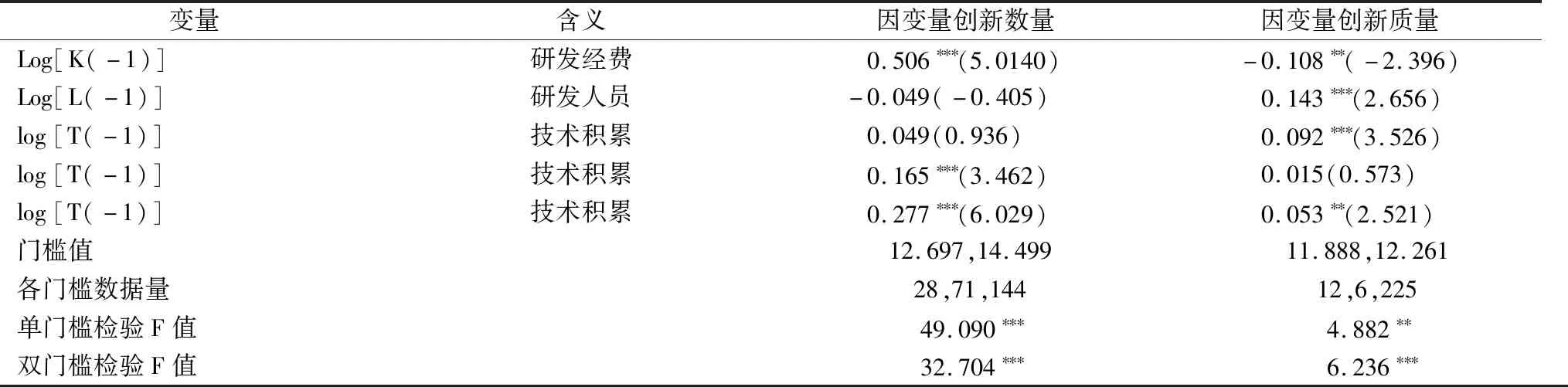
表4 技術積累的創新數量門檻估計結果Tab.4 Threshhold estimation results of technology accumulation′s innovation quantity

當因變量是創新數量時，創新數量存在兩個門檻，其對應值分別為12.697、14.499，將創新數量分為低水平、中等水平、高水平3類，數量分別為28、71、144個，以創新數量高水平地區為主。技術積累對創新數量的彈性系數分別為0.049、0.165、0.277，但第一個彈性系數沒有通過統計性檢驗。也就是說，當創新數量較低時，技術積累與創新數量無關，這是因為在上述情況下，企業創新能力弱，技術積累水平不高，兩者難以形成有效的互促關系。隨著創新數量增加，技術積累對創新數量的影響彈性逐步增強。

當因變量是創新質量時，創新數量存在兩個門檻，對應值分別為11.888、12.261，將創新數量分為低水平、中等水平、高水平3類，數量分別為12、6、225個，以創新數量高水平地區為主。技術積累對創新數量的彈性系數分別為0.092、0.015、0.053，但第二個彈性系數沒有通過統計性檢驗。也就是說，當創新數量較低時，技術積累對創新質量的影響彈性較大，但由于數據量太少，該結論價值不高。總體上，對于創新數量較多地區而言，技術積累對創新數量的彈性影響系數處于中等水平。

3.3.3 技術積累對創新數量、創新質量的創新質量門檻

分別以創新數量、創新質量作為因變量，研發經費、研發人員作為控制變量，技術積累作為核心變量，創新質量作為門檻變量，采用面板門檻回歸模型進行回歸，實證結果如表5所示。

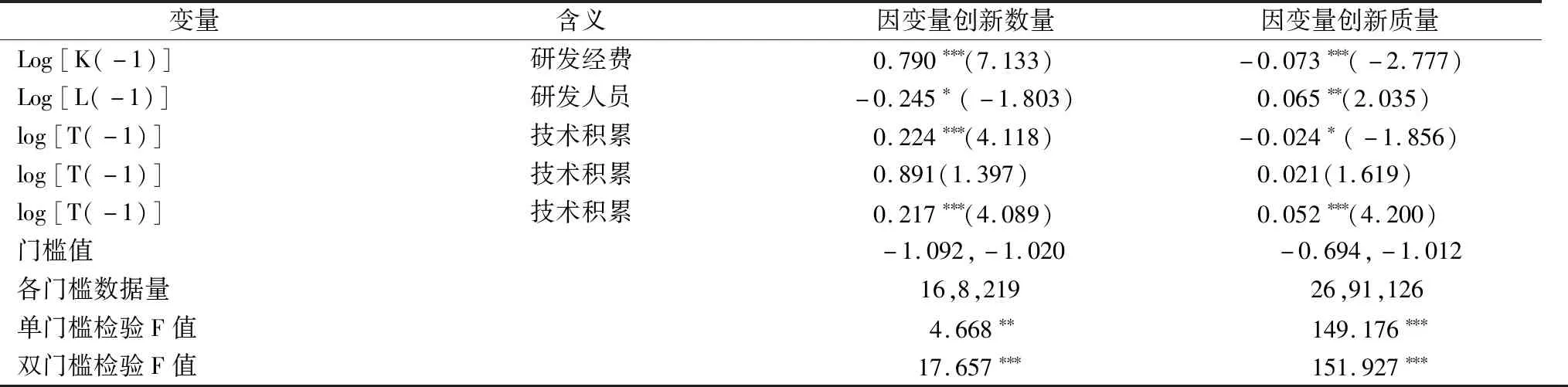
表5 技術積累的創新質量門檻估計結果Tab.5 Threshhold estimation results of technology accumulation′s innovation quality

當因變量是創新數量時，創新質量存在兩個門檻，對應值分別為-1.092、-1.020，將創新質量分為低水平、中等水平、高水平3類，數量分別為16、8、219個，以創新質量高水平地區為主。技術積累對創新數量的彈性系數分別為0.224、0.891、0.217，但第二個彈性系數沒有通過統計性檢驗。也就是說，當創新質量較低時，技術積累對創新數量的彈性系數較大，而當創新質量較高時，技術積累對創新數量的彈性系數較小。這是因為當創新質量較低時，企業技術積累的主要貢獻是提高創新數量，當創新質量較高時，企業技術積累對創新質量的作用更顯著，同時，對創新數量的彈性影響有所降低。

當因變量是創新質量時，創新質量存在兩個門檻，對應值分別為-0.694、-1.012，將創新質量分為低水平、中等水平、高水平3類，數量分別為26、91、126個。技術積累對創新質量的彈性系數分別為-0.024、0.021、0.052，但只有第三個彈性系數通過統計性檢驗，說明只有當創新質量較高時，技術積累才能有效促進創新質量提升，當創新質量較低或者中等時，技術積累難以有效促進創新質量提升。

3.3.4 技術積累對創新數量、創新質量的研發經費門檻

分別以創新數量、創新質量作為因變量，研發經費、研發人員作為控制變量，技術積累作為核心變量，研發經費作為門檻變量，采用面板門檻回歸模型進行回歸，實證結果如表6所示。

表6 技術積累的研發經費門檻估計結果Tab.6 Threshhold estimation results of R&D expenditure for technology accumulation

當因變量是創新數量時，研發經費存在兩個門檻，對應值分別為11.744、13.251，將研發經費分為低水平、中等水平、高水平3類，其數量分別為87、86、70個，數量相近。可以發現，技術積累對創新數量的彈性系數分別為0.223、0.313、0.277，均通過統計性檢驗。當研發經費處于中等水平時，技術積累對創新數量的彈性系數較高，其它情況下則較低。當研發經費較少時，由于保障創新數量的基本條件不具備，所以技術積累的彈性系數較小，而當研發經費充足時，技術積累的邊際貢獻會出現遞減，同樣，彈性系數也有所降低。

當因變量是創新質量時，研發經費存在兩個門檻，對數值分別為9.646、14.111，將研發經費分為低水平、中等水平、高水平三類，數量分別為14、205、24個，以研發經費中等地區居多。技術積累對創新質量的彈性系數分別為0.007、0.059、0.082，但第一個沒有通過統計性檢驗，說明當研發經費較少時，技術積累與創新質量無關，當研發經費水平逐步提高時，技術積累對創新質量的貢獻不斷增大。

3.3.5 技術積累對創新數量、創新質量的研發人員門檻

分別以創新數量、創新質量作為因變量，研發經費、研發人員作為控制變量，技術積累作為核心變量，研發人員作為門檻變量，采用面板門檻回歸模型進行回歸，實證結果如表7所示。可以發現，當因變量是創新數量時，研發人員存在兩個門檻，對應值分別為11.744、13.251，將研發人員分為低水平、中等水平、高水平三類，數量分別為25、161、57個，以中等水平人員居多。技術積累對創新數量的彈性系數分別為0.353、0.286、0.246，均通過統計性檢驗。這意味著隨著研發人員增多，技術積累對創新數量的彈性系數總體呈降低趨勢，符合邊際貢獻遞減規律。其根本原因是創新成果已經具有一定規模，在這種情況下，隨著研發人員增多，技術積累對創新數量的作用出現減弱。

表7 技術積累的研發人員門檻估計結果Tab.7 Threshhold estimation results of R&D personnel for technology accumulation

當因變量是創新質量時，研發人員存在兩個門檻，對應值分別為6.504、10.585，將研發人員分為低水平、中等水平、高水平三類，數量分別為11、206、26個，同樣以中等水平人員居多。技術積累對創新質量的彈性系數分別為0.009、0.062、0.086，但第一個彈性系數沒有通過統計性檢驗。這是因為科技人員是創新的重要力量，當研發人員較少時，技術積累難以提升創新質量。隨著研發人員增多，技術積累對創新質量的彈性系數逐步增大，符合我國創新質量提升空間較大的現實。

3.4 貝葉斯向量自回歸模型估計

建立貝葉斯向量自回歸模型，滯后期檢驗結果顯示滯后2期最佳，單位圓檢驗結果顯示所有的點都位于單位圓內，因此模型總體是穩健的。

創新數量的脈沖響應函數如圖3所示。可以發現，來自研發經費一個標準差的正向沖擊對其影響最大，當期為0，隨后逐漸提升并趨于穩定；其次是技術積累的沖擊，當期也為0，隨后略有提升并趨于穩定；再次是研發人員的沖擊，當期為0，總體作用較弱，但影響時間較長；最后是來自創新質量的沖擊，當期為0，隨后急劇下降，表現為負向彈性，作用時間較長，說明創新質量的沖擊不能提高創新數量。

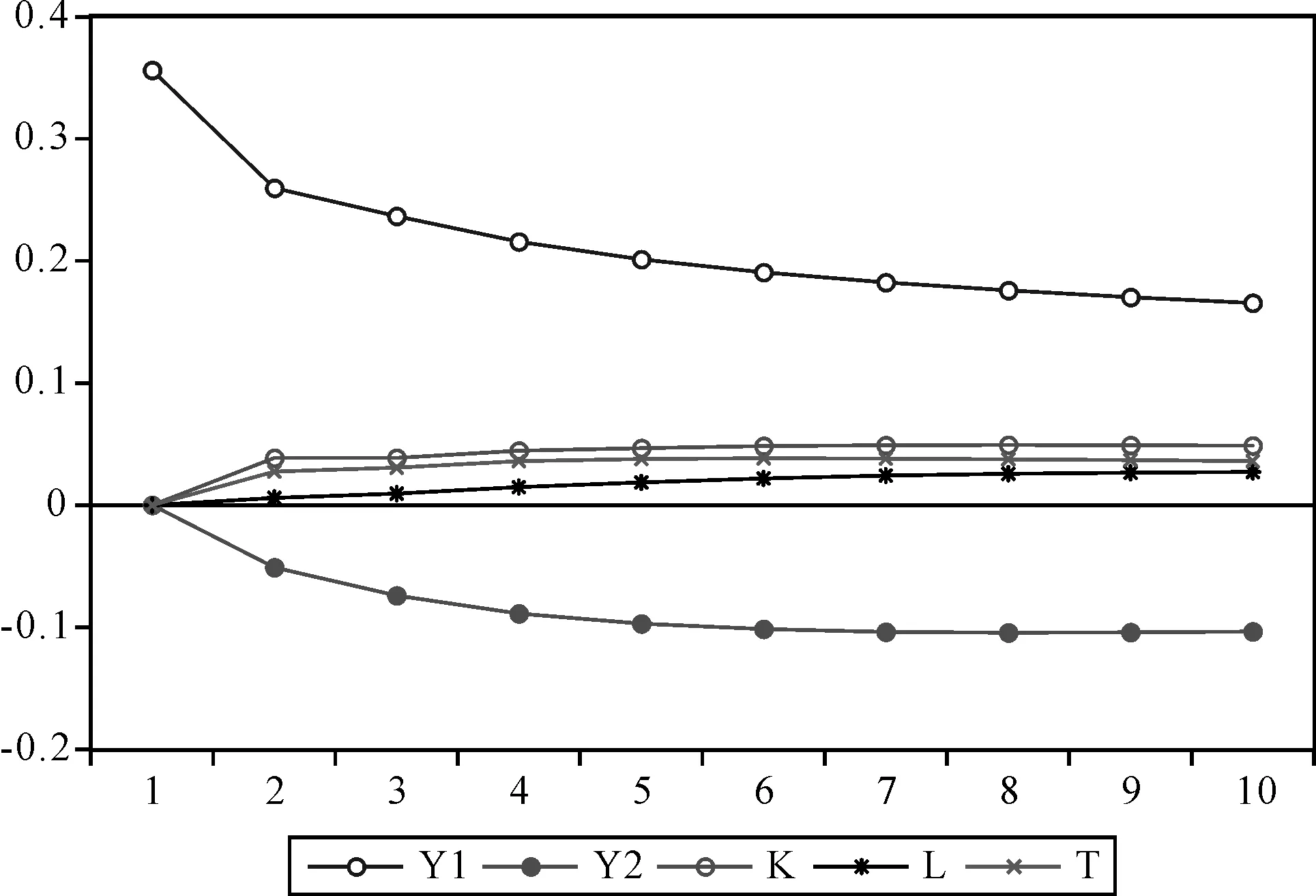
圖3 創新數量的脈沖響應函數Fig.3 Impulse response function of innovation quantity

創新質量的脈沖響應函數如圖4所示，可以發現，首先，研發經費的沖擊對其影響最大，當期為0，總體較弱，但是作用時間較長；其次是技術積累的沖擊，也比較弱，特征類似；再次是研發人員的沖擊，但結果顯示為負向彈性，總體較弱，說明研發人員的沖擊難以有效提高創新質量；最后是創新數量的沖擊，同樣表現為負向彈性，當期為0，作用時間較長，說明創新數量的沖擊難以提高創新質量。

圖4 創新質量的脈沖響應函數Fig.4 Impulse response function of innovation quality

技術積累的脈沖響應函數如圖5所示。可以發現，首先，研發經費一個標準差的正向沖擊對其影響最大，當期就發揮效用，至第四期達到極大值后略有下降；其次是創新數量的沖擊，當期發揮效用，隨后迅速提高，作用時間較長，說明創新數量對技術積累具有較強的正向反饋；再次是研發勞動力的沖擊，當期發揮效用，總體較平穩，作用時間較長；最后是創新質量的沖擊，其當期發揮效用，但是彈性系數總體不大，并且從第四期開始衰減為負數，說明創新質量對技術積累的反饋作用有待提高。

圖5 技術積累的脈沖響應函數Fig.5 Impulse response function of technology accumulation

3.5 穩健性檢驗

為了對技術積累與創新數量、創新質量的關系進行穩健性檢驗，以創新數量、創新質量作為產出，研發經費、研發人員、技術積累作為投入變量，基于BP人工神經網絡進行穩健性檢驗。人工神經網絡的學習閾值總誤差設定為0.000 000 1，一旦到達該閾值則停止學習。由于BP人工神經網絡模型每次學習結果不一樣，因此采用5次學習的平均值結果作為最終結果。

創新數量的穩健性檢驗結果如表8所示，可以發現，研發經費的權重最高，為46.15，其次是技術積累，權重為36.27，最小的是研發人員，權重為17.58，排序與式(1)-(6)的估計結果一致，說明研究結果穩健。

表8 穩健性檢驗結果Tab.8 Robustness test results

4 研究結論

4.1 技術積累對創新數量的貢獻大于創新質量

聯立方程估計結果表明，技術積累對創新數量的彈性影響要遠遠高于創新質量。各種面板門檻效應的估計結果也表明，技術積累對創新數量的彈性影響也遠遠大于創新質量。其主要原因是，我國創新數量總體較大，但創新質量不高，并且顛覆性創新、重大創新、重大生產工藝改進等相對滯后，新興技術積累、重大相關技術積累、重大生產技術積累不足。

4.2 創新數量與創新質量協調水平不高

聯立方程估計結果表明，創新數量對創新質量的彈性系數為負，創新質量對創新數量的彈性系數也為負。貝葉斯向量自回歸模型結果顯示，創新質量沖擊對創新數量的影響呈負向，創新數量沖擊對創新質量的影響總體較弱，但長期表現為負向。這充分說明我國高技術產業創新數量與創新質量協調度較低，盡管創新數量是創新質量的基礎，創新質量是創新數量的高端化，但由于創新質量不高，導致兩者不平衡。

4.3 技術積累對創新數量的貢獻中其自身、研發人員、創新質量的門檻效應呈遞減特征

在技術積累對創新數量的貢獻中，技術積累自身、研發人員、創新質量對其的彈性系數均為非線性，且作用特征相似，隨著這些門檻變量水平提高，技術積累對創新數量的彈性系數總體上呈降低趨勢。這說明從提高創新數量角度，技術積累盡管具有重要作用，但如果缺乏根本的基礎理論突破和重大技術突破，技術積累的作用有限。

4.4 隨著創新數量增加技術積累對創新數量的彈性影響系數逐步增大

當企業擁有較多創新數量和較高水平技術積累后，企業存在較大的選擇空間和更多技術路徑，因此更有利于創新數量增加。創新數量作為一種創新挖潛途徑，還有較大提升空間。

4.5 當研發經費處于中等水平時技術積累對創新數量的彈性影響系數最大

面板門檻回歸結果表明，當研發經費處于中等水平時，技術積累對創新數量的彈性影響最大。這是因為研發經費不足導致技術積累難以促進創新數量增加，而當研發經費水平較高時，企業能將更多精力放在提高創新質量上。

4.6 技術積累對創新質量的彈性影響具有較強的規模經濟效應

面板門檻回歸模型結果表明，當創新數量、創新質量、研發經費、研發人員以及技術積累自身水平較低時，技術積累與創新質量無關，只有當上述水平均有提高時，技術積累才與創新質量正相關，并且當研發經費、研發人員投入從中等水平提升到高水平后，技術積累的彈性系數才會有所增大，這主要是因為我國高技術產業規模不大、創新質量整體不高。