信息技術下的智慧課堂構建策略

李 蓉（湖南省長沙市芙蓉區修業學校）

信息技術所帶來的震撼和沖擊正深深地影響著現代教育。信息技術是從根本上改變數學學習方式的重要途徑之一，也是數學教學中重要的手段和策略。因此，每一位數學老師都必須熟悉和掌握信息技術，更新自己的教學觀念，與時代同步。

一、巧用課件演示，突破數學難點

華羅庚曾經說過：對數學產生枯燥乏味、神秘難懂的印象的主要原因就是脫離實際。我們可以利用多媒體課件構建生動活潑、有趣多樣的教學情境，并形象演示出知識抽象的部分，達到突破難點。

例如，五年級上冊《分段計費》一課，教師可以設計出租車收費問題，這是與學生生活息息相關的情境。城市每個孩子或多或少都乘坐過出租車，教師可以布置學生課前乘坐并了解出租車計費的方式。

農村孩子乘坐出租車的很少，老師可以課堂上課件先演示乘客坐車的情景并產生問題，讓城市學生回憶乘出租車的過程，農村孩子體驗乘出租車是怎么一回事。學生在解決問題時會遇到本課難點，不理解分段，第一段8千米以內的起步價也不好理解。特別是2千米以內8元，是每千米4元，還是無論走多遠都是8元？這里很容易讓學生思考得不嚴謹。

“分段計費”這還只是其中的一種方法，還有一種解法——“先假設再調整”，許多學生因調整的部分較為抽象很難接受。這兩種方法教師可以利用課件，通過數形結合的方式（線段圖），將“分段計費方法”中的起步價含義和“先假設再調整”中調整的部分是以前的少算部分，做動態演示。學生會有豁然開朗，眼前一亮的感覺，這種動態的數形結合演示很好地突破難點（圖略）。

二、幾何畫板繪制，展現圖形關系

幾何畫板以畫點、線、面為主，并提供平移、縮放、反射、旋轉等形狀變形功能，讓幾何對象的位置關系、運行變化規律等以動態的形式展示給學生，并提供相當豐富而方便的創作功能。通過幾何畫板的演示可以實現“靜止”到“運動”，“固定”到“變化”的系列過程。給予學生良好的直觀效果，建立良好的空間想象。

在六下復習平面圖形的知識一課中，幫助學生回憶整理所學過的平面圖形的面積計算公式及推導公式的過程，幾何畫板演示是老師們常用的教學模式。這些圖形的面積計算公式也是相互交錯和關聯的。求平行四邊形和三角形面積可以轉化成長方形，求梯形面積又可以轉化成這些基本圖形。

當梯形的上底會因為有拖動慢慢變大（如下圖1）；當梯形的上底等于下底的時候，轉化成一個平行四邊形（如下圖2）；梯形的上底在慢慢變短；當梯形的上底等于0的時候，轉化成一個三角形（如下圖3），并隨著圖形的變化顯示出相應的面積計算數據（如下圖4）。

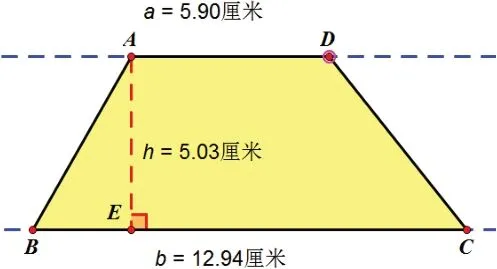
圖1

圖2

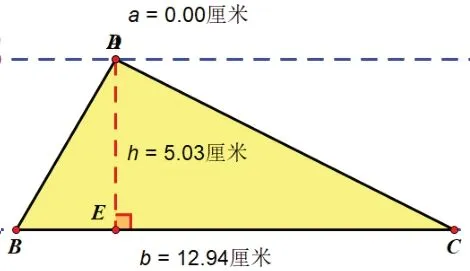
圖3

圖4

通過幾何畫板演示，學生對于圖形之間的關系一目了然，并為這種新型教學手段所驚嘆和震撼，它所實現的教學效果是一般教具所不能比擬的。

三、視頻延伸探究，拓寬學生視野

這里所說的視頻，是像播放微電影一樣，讓學生感受數學在真實生活中的應用。在數學學習中，有些問題或知識點，不是描述或想象就可以達到的，課堂上光靠教師講授還不能很好地讓學生理解和掌握。學生由于沒有看見實實在在的畫面，印象往往不是很深刻，視野也不會很廣闊。

在教學五年級上冊的《數對》一課時，為了讓孩子們感受數對在生活中的應用，欣賞了一些生活中的圖片，這也只是數對知識的一些基本應用。教師播放了北京申奧會中張藝謀導演用數對知識來表演方陣中的“和”字牌變化，學生受到強烈的視覺沖擊，印象頗為深刻。

又如，體育老師在操場畫圓等視頻，它很好地解決了學生因課堂有限空間帶來的認知障礙，也激發了學生課后探究及再思考的興趣。

四、信息軟件互動，拉近師生距離

如果說課件和微視頻是普遍使用的信息技術，那么微課和希沃軟件則是近幾年信息技術在教學應用中的升級版。它們的出現，讓信息技術又一次在教學中達到巔峰，實現師生零距離。微課，是現代教學中比較常用的模式。學生可以根據自身情況自由選取學習的內容、時間與進度，進行數學知識的學習與鞏固。如果學生在哪個單元的知識點上不清楚，或是對于某些題目的解答不理解，他可以反復觀看老師錄制的微課，來充分消化。甚至可以在軟件上留言，師生實現網上互動來進行交流答疑。

在沒有投影儀的情況下，只要有網絡，希沃軟件可以很好地實現手機與電視屏幕的投影。在教學中用手機拍照上傳至軟件中，電視屏會顯示我們需要展示的內容，在展示的內容上教師可以利用畫筆重復地在原圖上進行標注，實時點評，添加輔助線等，操作方便流暢。特別是幾何題目講解上，對圖形可以進行適當的放大和縮小，更加清晰。

以上提到的這些信息技術，都可以囊括在一個系統中，那就是互聯網。只要你肯上網搜索，幾乎沒有你找不到的，沒有它解決不了的。互聯網在改變著人類的生產生活，也為創新教育教學方式提供了良好的外部條件。

在教學中，可以利用互聯網的平臺和信息通信技術，推動移動互聯網、云計算、大數據、物聯網等，與小學數學教學深度融合，再次創造出一種嶄新的教學模式。它有著廣泛的應用前景，也必然對教學產生重大而深遠的影響。當校園內連接到互聯網時，學生不僅可以在教室內通過教室教學獲得知識，同時也可以在學習網站、學習論壇中查詢資料，實現課程的深入學習。甚至將網絡作為交流平臺，與教師、同學、外界進行交流討論等活動。

如在教授“斐波那契數列”這一知識點時，想讓學生在當堂課上就消化所學的知識還是很有難度的。關于斐波那契數列的知識也遠遠不止課堂上這些，教師可以布置學生課后再次繼續查閱與其有關的史料，第二天來進行匯報。學生通過互聯網上的搜尋，發現大量的課外信息。了解到此數列與黃金分割比之間的關系，以及數列中產生的數值作用不僅僅體現在繪畫上、還有雕塑、音樂（鋼琴鍵盤）、建筑等藝術領域，在管理、工程設計等方面也有著不可忽視的作用。真正實現學生學習能力的深度挖掘，為學生今后的數學學習和數學思考、數學應用奠定基礎。