Savitzky Golay-WPT在滾刀主軸振動信號降噪中的應用

李偉光，余秋霖，駱春林，孫菁瑤，林守金，龔德明

(1.華南理工大學機械與汽車工程學院，廣東廣州 510641；2.中山邁雷特數控技術有限公司，廣東中山 528437)

0 前言

刀具是對機械加工系統影響最大的加工要素，它的狀態決定了工件的加工質量。因此，準確識別滾齒刀磨損狀態能夠提高企業加工效率、降低經濟成本。然而，由于生產加工環境十分復雜，采集到的主軸振動信號受到環境因素和人為因素影響，往往存在許多噪聲。為減小噪聲對信號特征的影響，對它進行降噪尤為重要。

小波包降噪是一種常用的降噪方式，文獻[1]提出了一種基于互補總體經驗模態分解(CEEMD)的小波包變換降噪方法。文獻[2]提出了一種基于總體平均經驗模態分解方法(CEEMDAN)聯合小波包分析的降噪方法。文獻[3]提出了一種用于一維數字信號分析的譜圖小波閾值降噪方法。

許多學者通過改進閾值方式或結合其他降噪方法提高小波變換降噪性能，但常用的Heursure閾值、Donoho閾值等雖能對弱噪聲信號實現信噪分離，但對于強噪聲信號，效果并不理想。針對該問題，文獻[5]提出了一種基于樣本熵的改進小波包閾值降噪方法，雖能去除強噪聲，提高信噪比，但該方法用時較長，計算速度慢，不適用于在線實時降噪分析與故障診斷。文獻[6]使用最小二乘法降噪以提高信噪比，該方法速度快，但信號會出現失真。

基于以上分析，針對實驗中樣本點數較多且信噪比低、小波包降噪效果不佳的問題，本文作者提出一種結合最小二乘擬合原理的小波包變換(Wavelet Packet Transform，WPT)方法，將它應用于仿真實驗和滾刀主軸振動信號降噪實驗，并對所提方法進行驗證。

1 SG-WPT基本理論

1.1 SG基本理論

Savitzky-Golay方法(以下簡稱SG)通過線性最小二乘法將相鄰離散數據點的連續子集擬合為一個低次多項式來對信號進行降噪，是一種在時域內的多項式最小二乘法擬合濾波方法。該方法最大的特點在于在濾除噪聲的同時可以確保信號的形狀、寬度不變，其原理如下：

一組以=0為中心的2+1個數據點可以用如下多項式擬合。

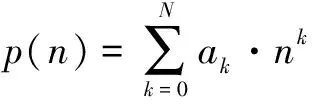
(1)

其最小二乘擬合殘差為

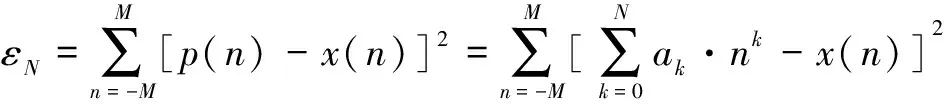
(2)

當式(2)中殘差取最小值時擬合效果最好，而后通過移動該窗口數組即可得到原始數據的所有擬合點。在擬合過程中，過于偏離正常趨勢曲線的噪聲部分會被丟棄，因而該方法能夠對數據起到平滑濾波的作用。

1.2 小波包基本理論

如圖1所示，小波分解只對信號低頻部分進行分解，不會對信號高頻部分進行分解。小波包針對該問題進行了改進，不僅對上一層分解得到的信號中的低頻部分進行分解，而且對高頻部分再一次進行分解。因此，對比同層次小波分解，小波包分解后高頻信號細節更全面。小波包分解方程：

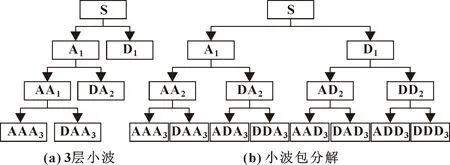
圖1 3層小波與小波包分解

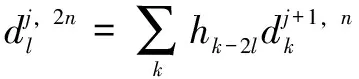
(3)

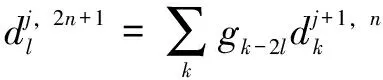
(4)

式中:-2、-2分別為小波包分解中的高、低濾波系數。

小波包重構方程如下：

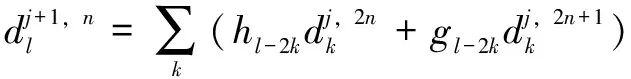
(5)

式中:-2、-2分別為重構小波包高、低濾波器系數。

1.3 SG-WPT降噪流程

SG-WPT方法降噪流程如下：

(1)選定小波基函數和標準熵，確定最佳小波分解樹，進行小波包變換，得小波包系數。信號分解的層數過大或者過小都會影響降噪性能，所以確定最佳小波分解樹尤為重要。首先，通過均方根誤差的穩定性確定最優分解層次；然后，比較底層子節點和父節點的代價函數值，若子節點函數值大于父節點，則父節點替代子節點。

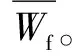
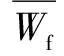
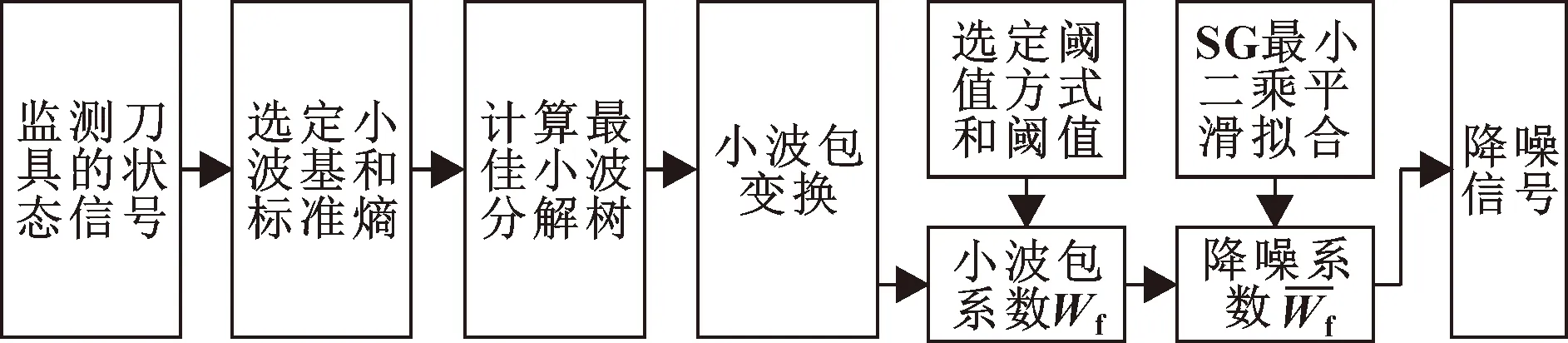
圖2 SG-WPT降噪流程

2 仿真信號降噪實驗

為驗證該方法的有效性和可行性，采用Blocks、Bumps、Heavy sine和Doppler 4種經典仿真信號進行降噪實驗，并與其他方法對比。

2.1 降噪性能評價指標

常用的降噪性能評價指標有很多，為直觀體現降噪性能，采用信噪比(SNR)作為降噪效果的評價指標。

信噪比定義為

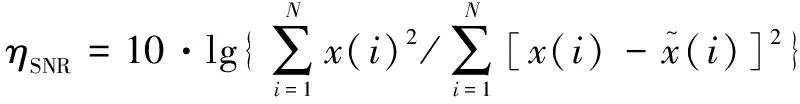
(6)

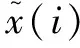
由式(6)知，對于輸入信噪比相同的信號，降噪后輸出信噪比越大，降噪性能越好。

2.2 仿真信號降噪實驗

設定仿真信號輸入信噪比為10 dB。樣本點個數與工程應用相對應，設定為16 384(2)。

仿真信號降噪實驗流程如下：

(1)生成仿真信號的原信號，添加輸入信噪比為10 dB的高斯白噪聲，得到加噪后的仿真信號;

(2)采用SG-WPT方法對加噪后的仿真信號進行降噪，得到降噪后信號;

(3)計算降噪后信號與原信號的輸出信噪比。

表1所示為仿真信號降噪流程，對原信號增加為10 dB的噪聲信號后，原信號被噪聲信號嚴重淹沒，特征難以識別。4種仿真信號經SG-WPT降噪后，仿真信號中大部分噪聲被去除，恢復了原信號的基本特征，輸出信噪比均達到20 dB以上，信噪比提升明顯。

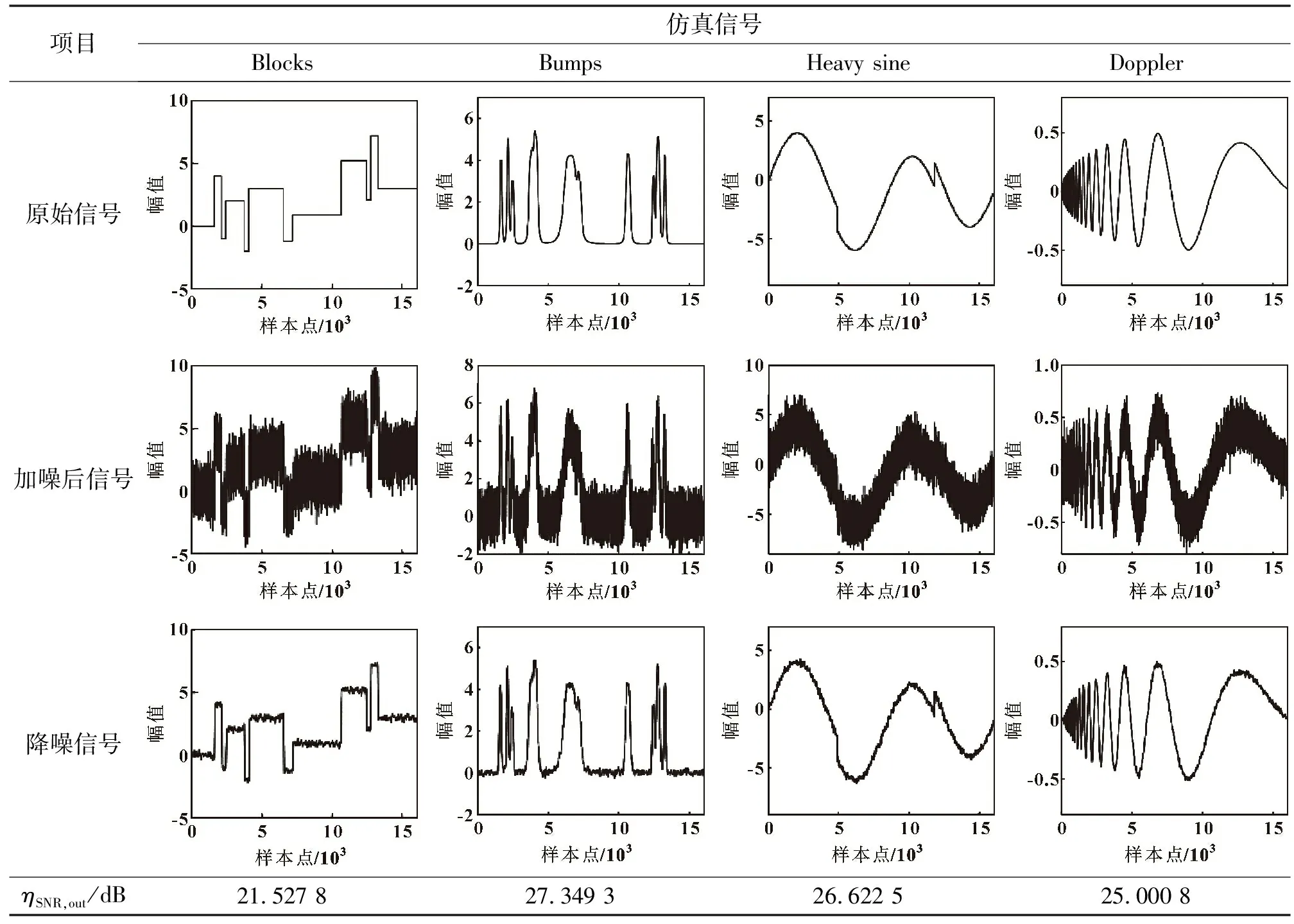
表1 仿真信號降噪實驗流程

分析仿真實驗結果可得：SG-WPT方法具有較強降噪能力，能大幅減小噪聲并避免原信號損失，使被噪聲嚴重污染的信號恢復特征。

2.3 不同階數降噪性能對比

選定上文所述4種仿真信號，設定其為10 dB，分別進行1～10階SG-WPT降噪。由圖3可知:當擬合階數為1時，Bumps、Heavy sine和Doppler 3種仿真信號的最大，均到達25 dB以上，隨著擬合階數的增大，出現陡然減小后逐漸減小的趨勢；Blocks仿真信號,其出現在1～3階緩慢增大，在3階以后逐漸減小的趨勢。4種仿真信號在6階擬合處，大小趨近一致，且下降趨勢變緩，相對于1階擬合平均下降了22.68%。綜上分析，第1階為最佳擬合階數。

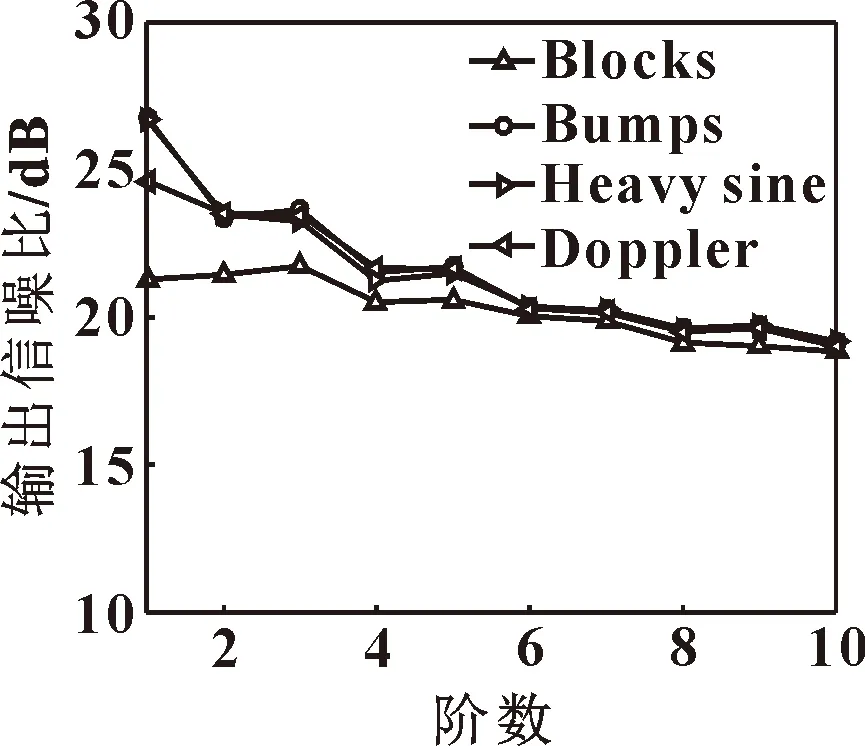
圖3 不同階數下的信噪比輸出

2.4 與其他降噪方法的性能對比

完備集合經驗模態分解(CEEMDAN)是一種在 EMD 基礎上改進的方法，它克服了傳統EMD方法的模態混疊現象，解決了 EEMD 方法中計算量大、分解完備性差等問題。

經典小波包閾值降噪方法是由小波降噪改進而來，其中，“db7”、“sym5”、“coif1”和“demy”等小波基具有較好的降噪效果，“db7”與“sym5”小波基的降噪性能相近，且優于“coif1”小波基。因此，選取“db7”和“demy”小波基進行對照實驗。用文中提出的方法與以上3種方法進行對比實驗，設定4種經典仿真信號輸入信噪比從-20 dB遞增到10 dB，小波包分解均采用3層分解。

表2所示為4種經典仿真信號輸出信噪比隨輸入信噪比的變化趨勢。由表2第2行可知，“db7”和“demy”小波基的降噪性能相近，降噪性能隨信噪比提高逐漸提升；CEEMDAN方法在信噪比較低時，4種仿真信號輸出信噪比提升幅值保持在4 dB左右，當輸入信噪比達到5 dB以上，降噪性能大幅提升,信噪比提升均值為4.44 dB；而文中所采用的SG-WPT方法在信噪比較低時也能表現出良好的降噪性能，4種仿真信號信噪比提升均值達到16.60 dB。綜述所述，在4種仿真信號降噪實驗中，SG-WPT方法降噪性能相比于小波包和CEEMDAN降噪性能有較大改善，解決了文獻[4]中方法存在的問題。

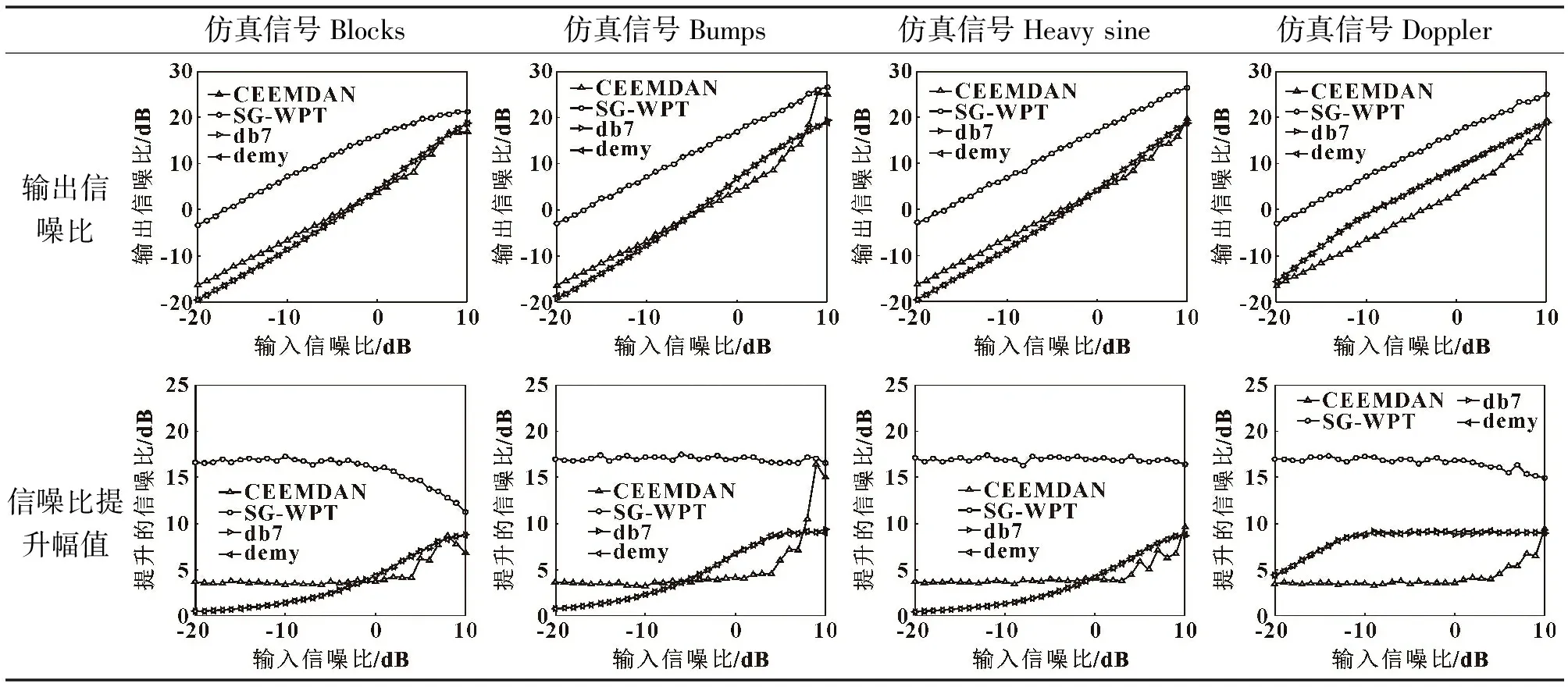
表2 輸出信噪比隨輸入信噪比變化趨勢

由表3可知：CEEMDAN-相關系數法計算量大，耗時達293.872 s，明顯長于小波包降噪方法；SG-WPT降噪方法耗時略高于“db7”小波基降噪方法；而“demy”小波基降噪方法耗時高于SG-WPT方法49.3%。從耗時上分析，SG-WPT方法能夠滿足時間短、反應快的需求，解決了文獻[5]中存在的問題，更符合工業生產加工過程中在線實時降噪分析與故障診斷的要求。

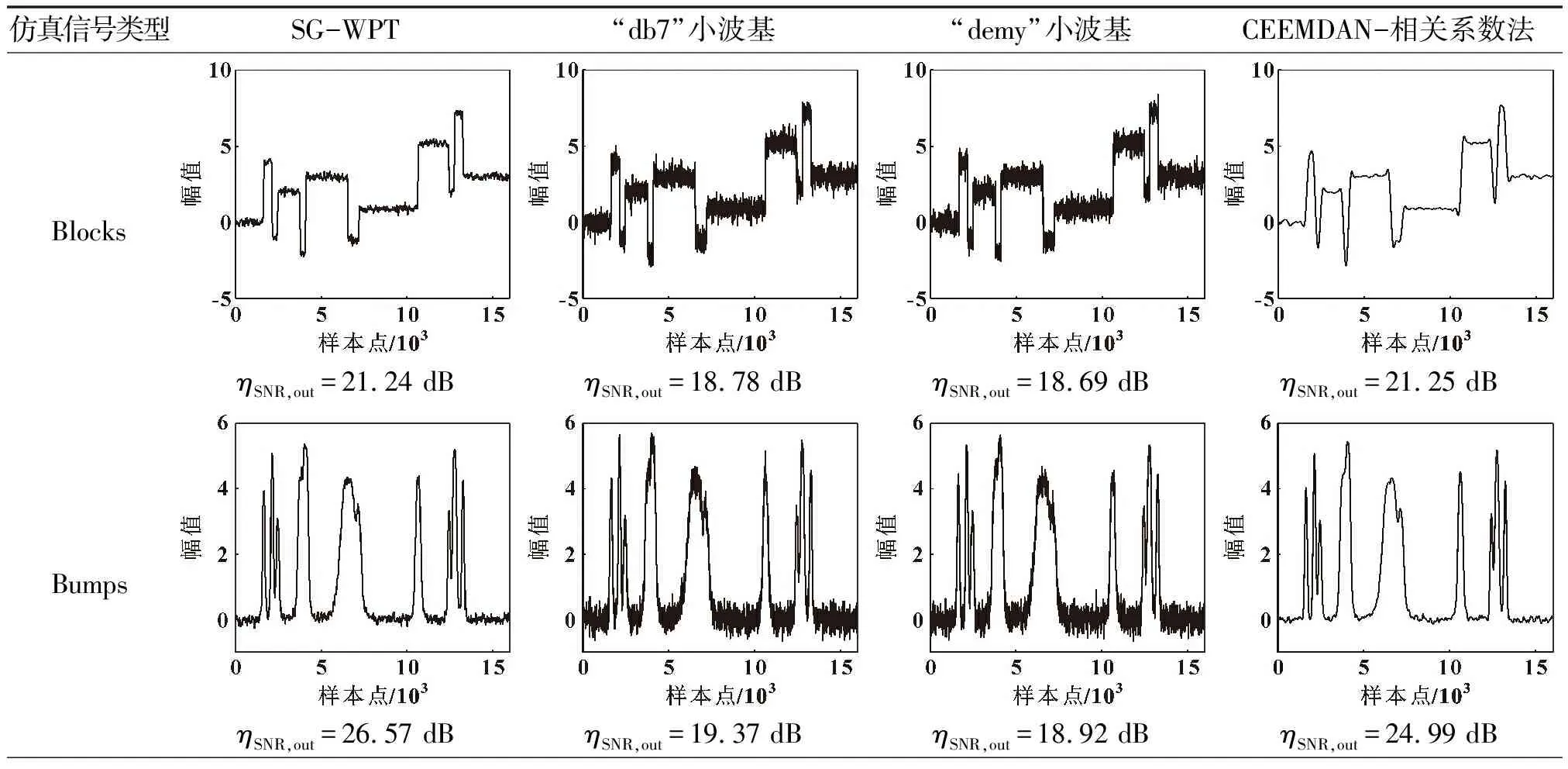
表3 4種方法對仿真信號降噪結果

由表3可知：“db7”與“demy”小波基降噪后仍殘留較多噪聲信號，難以甄別信號特征；CEEMDAN-相關系數法降噪后會出現信號失真現象，如Heavy sine仿真信號降噪后時域圖中框選部分所示，階躍信號被抹去，喪失了原信號的特征，因此穩定性不夠；SG-WPT方法，在濾除噪聲的同時減少了原信號特征損失，因此輸出信噪比明顯提高。對于4種仿真信號，當輸入信噪比為10 dB時，文中方法輸出信噪比相比于傳統小波包和CEEMDAN平均提高了31.35%和16.36%。

綜上所述，對于信噪比較低的仿真信號，文中提出的SG-WPT方法不僅能有效濾除噪聲，還能夠避免信號失真且計算速度快，彌補了傳統小波包閾值降噪性能差的缺陷，優于傳統小波閾值方法和CEEMDAN-相關系數法。

3 滾刀主軸振動信號降噪應用

3.1 滾刀主軸振動信號采集

為驗證文中方法在實際工程信號處理中的有效性，在某數控機床生產廠進行了滾齒加工實驗，采集到了主軸振動信號。圖4所示為滾刀振動信號采集現場，為防止因切削液沖擊而導致傳感器脫落，在方向上安裝了2個PCB加速度傳感器，采集滾齒機加工過程中滾刀主軸向和向振動加速度信號，采樣頻率為12 800 Hz。加工過程中，滾刀主軸振動信號經PCB加速度傳感器、LMS信號采集儀后傳入計算機進行存儲和顯示。

圖4 滾刀振動信號采集現場

在靠近滾刀的2號傳感器采集到的信號中截取16 000個采樣點作為滾刀當前加工狀態的振動信號，并對該信號進行分析處理。

3.2 滾刀自轉頻率和滾切頻率

采集到的滾刀主軸振動信號中有用信號包括滾刀主軸自轉頻率和滾切頻率，它們是滾刀主軸振動信號特性的主要體現，可通過表4中影響滾刀主軸振動信號分析的滾齒機主要加工參數計算。

表4 影響振動信號分析的主要加工參數

滾刀主軸自轉頻率：

=60

(7)

滾刀滾切頻率：

=60

(8)

由表4中參數和式(7)(8)可計算出滾刀主軸自轉頻率和滾刀滾切頻率，如表5所示。

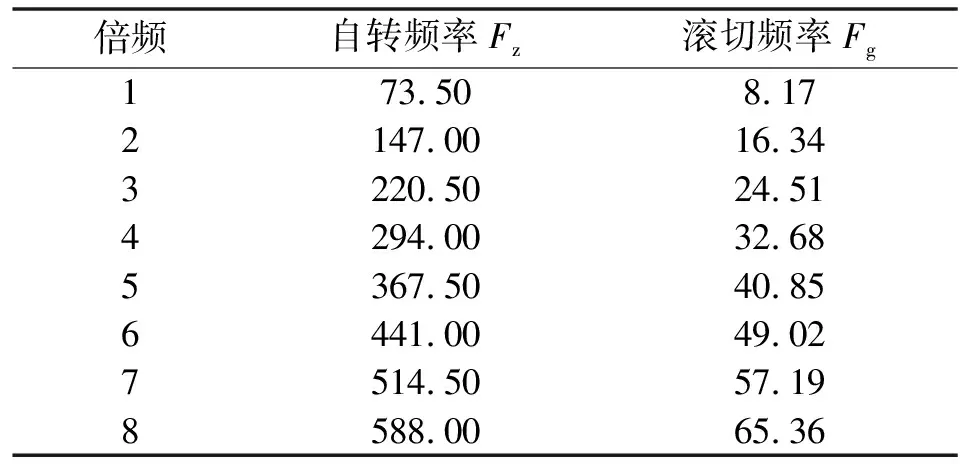
表5 自轉頻率和滾切頻率倍頻 單位：Hz

3.3 滾刀主軸振動信號降噪性能分析

由于CEEMDAN相關系數法耗時長、穩定性差且“db7”與“demy”小波基降噪性能相似，選取耗時稍短的“db7”小波基與SG-WPT進行滾刀主軸振動信號降噪對比實驗。對降噪前后的信號分別進行FFT、包絡譜和小波終端節點的彩色系數分析，結果如表6所示。可知：針對降噪前后FFT頻域圖，可見滾刀主軸振動原信號頻率在4 500 Hz以下；“db7”小波基降噪后，1 000 Hz以上噪聲基本濾除，但1 000～2 000 Hz頻段依然存在部分噪聲，能提取1～7倍滾切頻率(～7)；SG-WPT方法降噪后，1 000 Hz以上噪聲完全濾除，能有效提取1～8倍滾切頻率特征(～8)，但FFT卻沒有有效提取出自轉頻率。因此，對其低頻部分采用包絡譜分析方法以提取其自轉頻率。

對信號先進行Hilbert 變換后，再進行 FFT可得到信號的包絡譜。如表6第3行所示，對比降噪前后0～70 Hz包絡譜頻域圖可知，“db7”小波基和SG-WPT方法均能將自轉頻率特征(～8)提取出，但SG-WPT降噪后，周邊信號干擾明顯減少，中心頻率更突出。

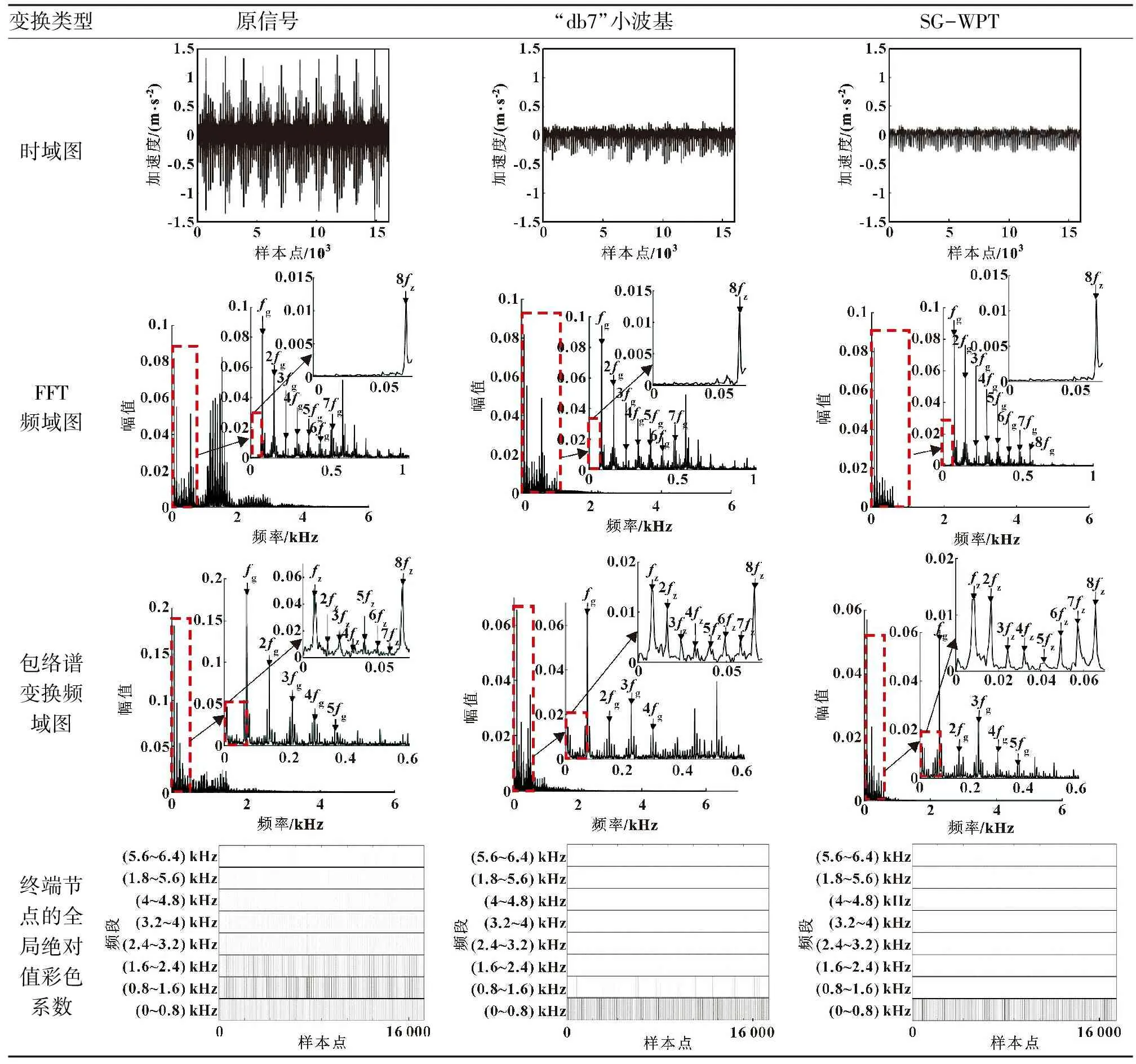
表6 降噪前后對比

由式(7)(8)可知，主軸自轉頻率與滾切頻率存在倍率關系，因相互疊加影響，導致包絡譜變換后，滾切頻率在5倍頻后出現中心頻率不準確現象。因此，為取長補短，對頻率相對較低的主軸自轉頻率采用包絡譜方法進行分析，而對頻率相對較高的滾切頻率采用FFT進行分析。

3層小波包將原信號分為8個終端節點，每個終端節點的全局絕對值彩色系數圖中灰色線條表示信號在該段樣本點內，存在對應于左側頻段的頻率，顏色越深，能量和幅值越大。由此可知，原信號頻率主要在0～2 400 Hz頻段，經“db7”小波基降噪后，在800～1 600 Hz頻段仍存留部分信號；SG-WPT降噪后，信號中800 Hz以上頻段基本去除，有效提取了主軸自轉頻率與滾切頻率，降噪效果明顯。綜合上述分析，在滾刀主軸振動信號降噪應用中，文中提出的SG-WPT優于經典小波閾值降噪方法，降噪性能突出。

4 結論

(1)針對采樣點較多信號CEEMDAN方法計算量大耗時長、經典小波包降噪效果不佳的問題，本文作者提出了一種基于最小二乘法平滑擬合的SG-WPT方法。將SG-WPT方法應用于仿真實驗，結果表明該方法對于實驗中的強、弱噪聲信號均表現出良好的降噪性能，相比于傳統小波包和CEEMDAN分別提高了31.35%和22.71%。

(2)將SG-WPT方法應用于滾刀主軸振動信號降噪實驗中，結果表明該方法能去除信號中的高頻噪聲，使主軸自轉頻率與滾切頻率周邊信號干擾明顯減少，中心頻率更為突出，降噪效果優于傳統小波閾值降噪。

(3)在降噪后滾刀主軸振動信號頻譜分析過程中，對比FFT和包絡譜分析，包絡譜分析能更準確地提取主軸自轉頻率，而FFT能更準確地提取滾切頻率，在頻譜分析過程中可結合兩者優點，取長補短。