基于優化極限學習機的渦軸發動機轉子碰摩故障診斷

黃磊，戴金躍，胡陽，彭俞根

(1.江蘇航空職業技術學院航空工程學院，江蘇鎮江 212134；2.中國航發北京航空材料研究院，先進高溫結構材料重點實驗室，北京 100095)

0 前言

渦軸發動機作為直升機動力源，無論在通航運輸還是部隊作戰，其運行狀態、工作環境都決定著飛行任務是否能夠如期完成。由于渦軸發動機機動性能多變，飛行任務包線不如民航渦扇發動機規律，經常會在轉子過渡態—穩態之間發生瞬間失衡現象，而這種現象會導致發動機出現短暫的碰摩現象。

目前，監控發動機轉子狀況，常采用分析安裝在發動機機匣上各測點振動加速度傳感器采集的振動信號的方法。但機匣測點上采集的振動信號通常屬于耦合信號，需要對振動信號進行有效處理后，才能夠有效識別出轉子故障，而類似于短時傅里葉、小波變換等信號處理方法均存在一定的局限性。因此，部分振動信號的故障診斷采用振動信號分析與診斷算法相結合的方法。

針對渦軸發動機出現的碰摩故障，MUSZYNSKA、袁惠群、褚福磊、WILLIAMS等學者的研究，使得轉子碰摩實現從原理分析到數學求解、從有限元仿真到實物模擬，并到工程應用。隨著碰摩理論的深入研究，針對不同情況而進行的碰摩研究較多。王四季等以對轉雙轉子局部碰摩為研究對象，對高壓、低壓、高低壓轉子碰摩進行實驗分析，并通過頻譜分析得出碰摩故障能夠通過和頻進行診斷。但對于基于振動信號分析的識別方法，如果事先未知故障頻譜特征成分表現形式，則難以進行故障識別。因此，本文作者針對某渦軸發動機渦輪機匣振動測點采集的數據，對頻譜進行分析，提取振動特征參數，結合優化極限學習機，對渦軸發動機燃氣渦輪碰摩、動力渦輪碰摩等狀態進行識別。

1 極限學習

極限學習機(Extreme Learning Machine, ELM)網絡通過隨機產生輸入層與隱含層的連接權值和閾值，并基于Moore-Penrose算法計算極限學習機網絡的輸出，實現了避免單隱層前饋神經網絡的缺陷，因而廣泛用于數據壓縮、特征學習、聚類、診斷等領域。HUANG等對極限學習機理論進行嚴格的數學論證，表明它能夠逼近任意的非線性分段函數。

假設有個獨立樣本(,)，=[1,2,…,]∈、=[1,2,…,]∈，具有個隱含層節點且隱含層與輸出層激活函數分別為()、()的單隱層前饋神經網絡結構如圖1所示，數學表示如式(1)所示。

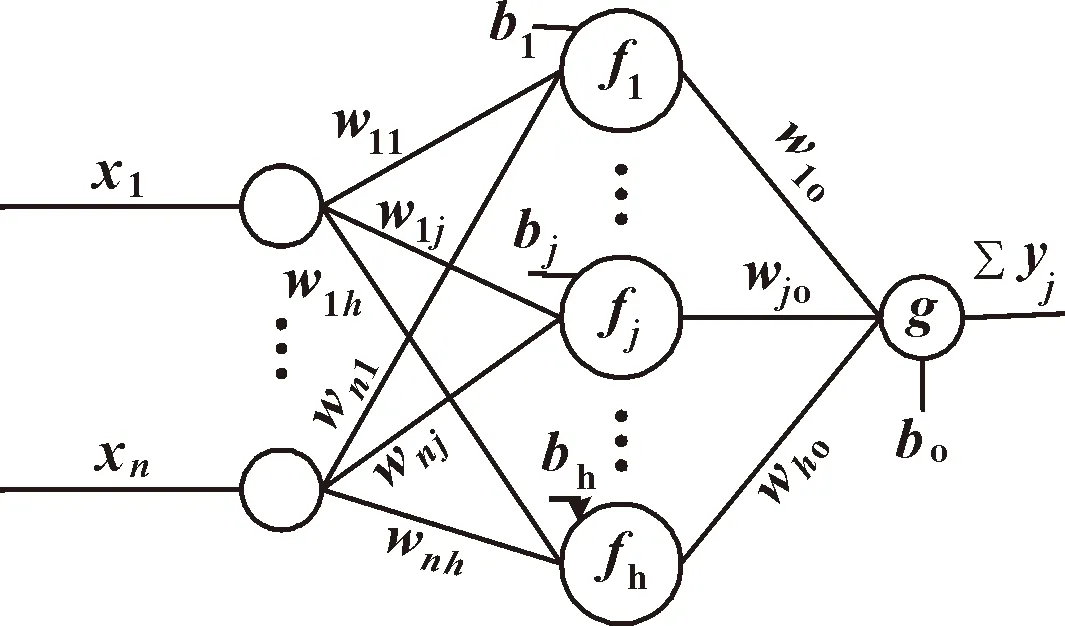
圖1 極限學習機網絡結構

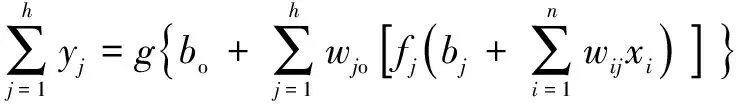
(1)

式中：為輸入變量，=1,2,3,…，；為輸入變量與隱含層神經元的連接權值；o為隱含層神經元與輸出層的連接權值；為隱含層神經元的閾值，=1,2,3,…,；為輸出層神經元的閾值。

如果為0，且()為線性激活函數時，將個獨立樣本代入式(1)簡化可得式(2)：

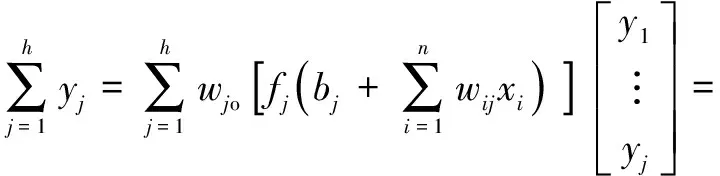
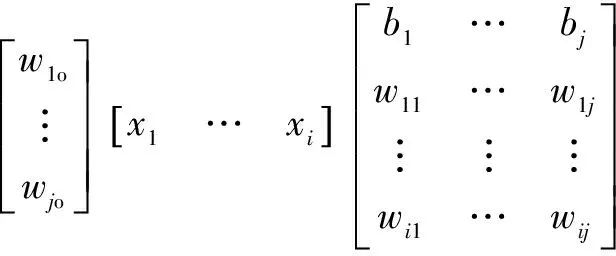
(2)

==?=

對于式(2)，如果存在觀測樣本，同時∈×、≥且()=，則的Moore-Penrose廣義逆可表示為

=()

(3)

將式(3)代入式(2)可得出極限學習機輸出權值向量：

==()

(4)

極限學習機中常用的激活函數有幾種，文獻[9,12]對不同激活函數進行了研究。本文作者基于這些文獻研究結果，選擇Sigmoid()函數作為激活函數。

2 優化的極限學習機

極限學習機能有效避免部分前饋神經網絡存在的缺陷，但它相比其他網絡可能需要更多神經元。同時，其隨機權值的賦予，可能會導致病態問題的產生，故采用遺傳算法進行優化。

遺傳算法的誕生得益于生物基因間的變異、交叉、選擇，是一種被廣泛應用于不同行業的智能尋優算法。隨著遺傳算法的不斷應用，也逐漸暴露出搜索能力受交叉變異概率影響等缺陷。因此，本文作者采用改進遺傳算法對極限學習機進行優化，并運用到后續轉子故障診斷。

2.1 遺傳算法

遺傳算法中基因個體的選擇沿用輪盤賭方式執行，假設個體累積概率為、個體適應度函數為()、輪盤旋轉次數為，則個體累積經驗選擇概率可表示為

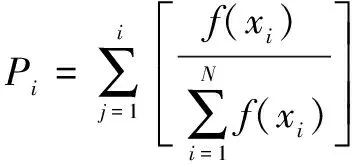
(5)

在遺傳算法中，變異操作能改變種群個體的結構，是影響遺傳算法搜索的關鍵。因此，應在保證種群多樣性的同時提高算法搜索能力。本文作者借鑒文獻[14]中的方法引入高斯變異，采用如式(6)所示的變異操作方式：

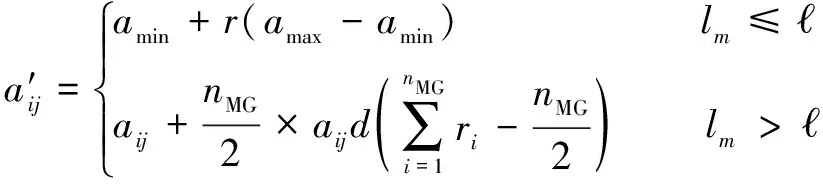
(6)

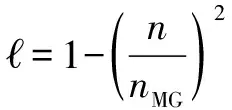
=min{-,-}

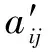
交叉、變異操作均采用多點方式進行(每次變異點數為當前基因數的50%，變異位置隨機選擇)，其操作示意分別如圖2、圖3所示。

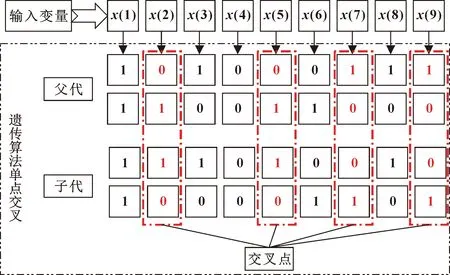
圖2 多點交叉

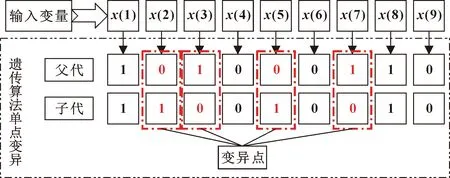
圖3 多點變異

2.2 優化的極限學習機

優化的極限學習機是采用遺傳算法優化極限學習機中隱含層神經網絡的權值和閾值。優化的極限學習機主要分為兩部分：一部分是遺傳算法根據個體適應度，不斷進行個體基因交叉、變異、選擇，每次迭代更新過程中需要更新最優個體，迭代結束后最優個體基因序列值即為極限學習機中隱含層神經網絡的權值和閾值；另一部分是極限學習機部分，極限學習機在接收到每次迭代更新的最優個體時，計算當前個體下輸出權值和適應度函數，并將結果反饋給遺傳算法，用于遺傳算法迭代計算。優化極限學習機流程如圖4所示。

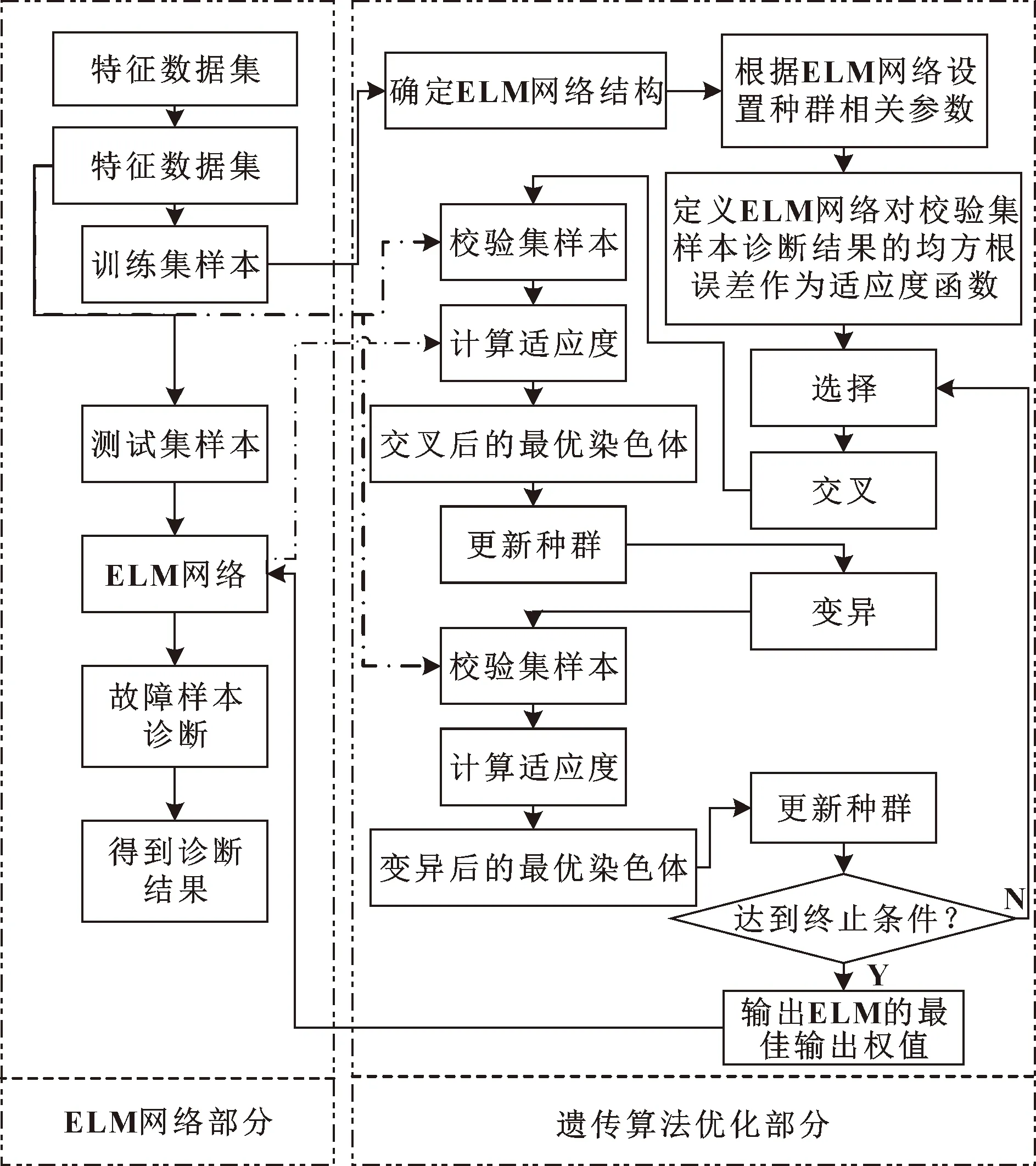
圖4 優化的極限學習機流程

優化極限學習機診斷流程描述如下：

(1)基于待診斷數據樣本類型確定ELM網絡的結構，并定義遺傳算法種群適應度函數；

(2)初始化遺傳算法基本參數，并對種群中個體的基因序列值進行二進制編碼；

(3)對種群進行交叉、變異、選擇操作，產生新的個體，即可行解；

(4)將所得到的可行解代入極限學習機中，通過Moore-Penrose方法計算ELM網絡輸出權值矩陣，并計算當前個體適應度，遍歷整個種群找到局部最優解，并更新全局最優解；

(5)算法終止判斷:若滿足算法終止條件，則輸出遺傳算法全局最優解，并代入極限學習機中；若否，則重復步驟(3)—步驟(5)；

(6)用Moore-Penrose方法計算極限學習機輸出權值矩陣，并對故障樣本進行診斷。

3 轉子碰摩實驗

3.1 轉子碰摩數據來源描述

渦軸發動機轉子振動碰摩數據源自某型號軍用發動機，由于信息保密的原因，以發動機渦輪機匣測點為碰摩振動監測點，從渦軸發動機試車數據中提取并稍加處理動力渦輪、燃氣渦輪轉子的0.5、1、2、3、4倍頻，進而構建渦軸發動機的振動包絡曲線，經過處理后的發動機正常狀態包絡線幅值如圖5所示。以圖6所示的試車轉速曲線(燃氣渦輪最大轉速為36 700 r/min、動力渦輪為25 400 r/min)還原振動信號，渦輪機匣測點的采樣頻率為10 kHz，模擬時間為3 min。模擬振動信號包括渦軸發動機正常狀態、燃氣渦輪轉子碰摩、動力渦輪轉子碰摩、燃氣與動力渦輪碰摩4種，碰摩故障發生點都在轉子轉速達到最大轉速后0.02 s處。

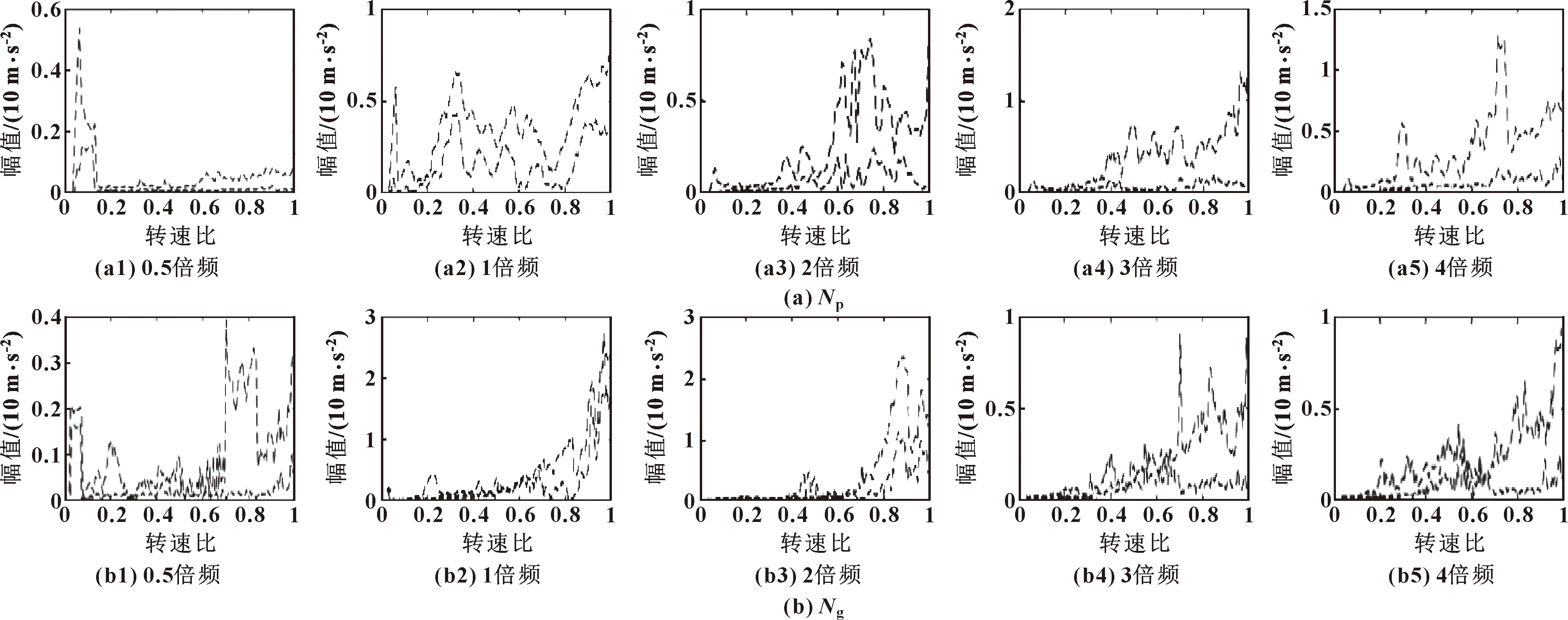
圖5 振動包絡曲線

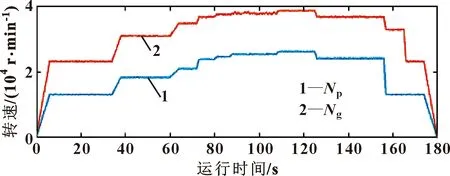
圖6 轉速曲線

3.2 轉子碰摩振動信號分析

渦軸發動機發生碰摩段的燃氣渦輪轉子轉速為36 700 r/min、動力渦輪轉速為25 400 r/min，各基頻幅值分別為611.7、423.3 Hz，分別記為、。渦軸發動機正常狀態、燃氣渦輪轉子碰摩、動力渦輪轉子碰摩、燃氣與動力渦輪碰摩4種狀況的振動信號和快速傅里葉變換(Fast Fourier Transform，FFT)頻譜如圖7所示。可知：正常狀態與碰摩故障狀態下的振動信號、頻譜信號存在較明顯差異，碰摩狀態更加凸顯次諧波的存在；但對于另外3種碰摩狀態，從振動信號上而言，不存在明顯的區別，但頻譜圖卻存在較為明顯差異，頻譜中均存在主頻、次頻、和頻成分；基于文獻[8]中的結論，根據和頻的出現可判斷碰摩故障的發生。

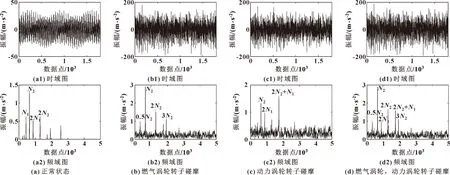
圖7 轉子碰摩振動信號分析

3.3 轉子碰摩數據提取與處理

由圖7可知，如不具備對碰摩故障信號的分析經驗，難以從振動信號或頻譜信號中直接分析出碰摩故障或碰摩故障類型，但碰摩故障特征會表征在振動信號的特征指標中。因此，本文作者提取振動信號的偏度指標、均方根指標、波形指標、脈沖指標、峰值指標、裕度指標，并基于第2節提到的優化極限學習機對碰摩故障進行診斷。

每類工作狀態下數據集均為120組，共計480組數據，部分數據如表1所示。可以發現：不同狀態下的碰摩故障所引起的特征指標變化趨勢存在差異，且各指標之間數量級差異明顯，容易增加數據級所導致的診斷誤差，因此按式(7)進行歸一化處理：

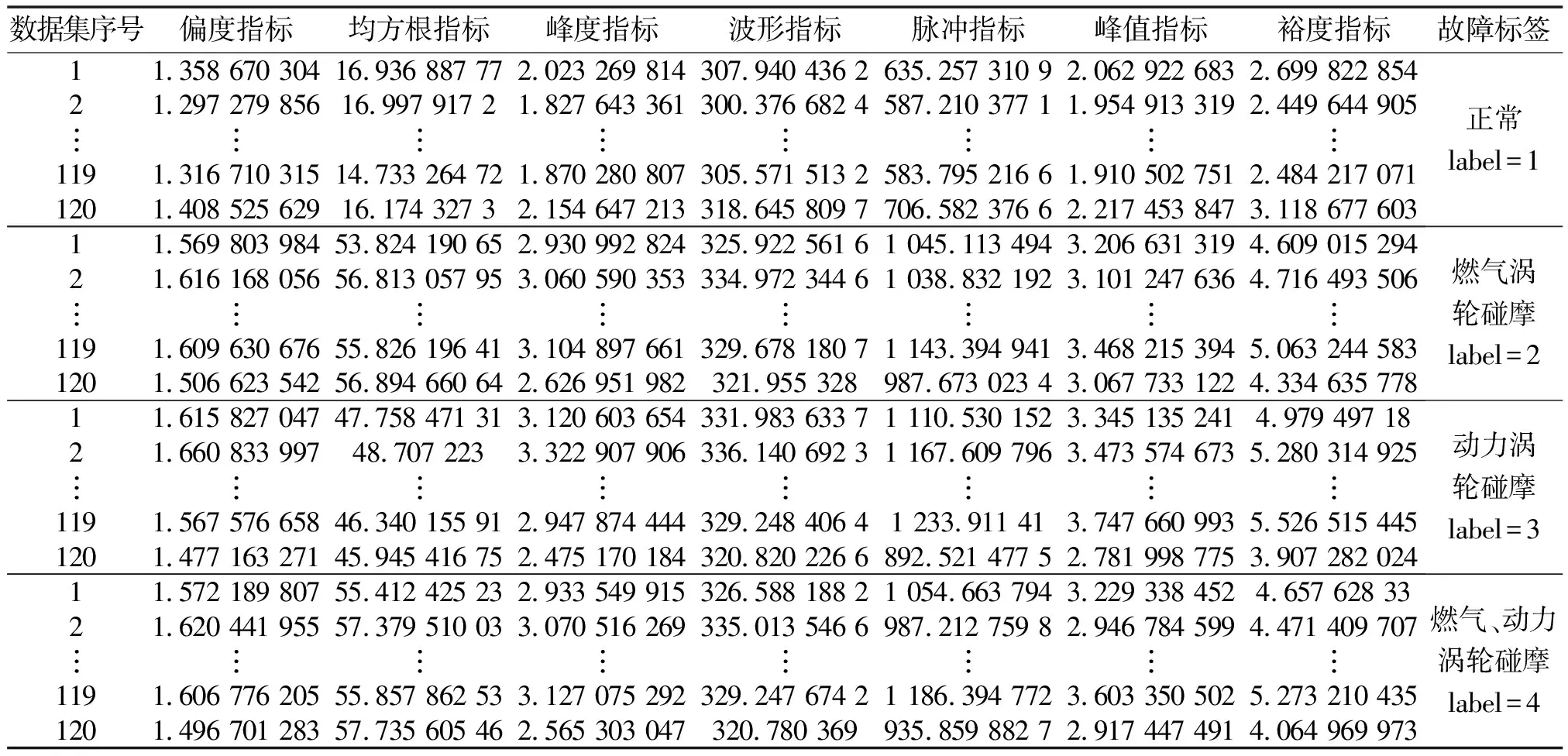
表1 特征指標數據集

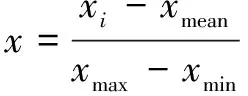
(7)

其中：、和分別表示特征指標的最大值、最小值和平均值；表示特征指標的第個值；表示歸一化后的值。

4 轉子碰摩故障診斷

基于第3節得到的轉子碰摩數據，采用文中提到的優化極限學習機模型對碰摩故障類型進行診斷。算法參數設置：遺傳算法種群大小為30、迭代步數200、種群范圍為[-0.5 0.5]；極限學習隱含層神經元個數由后續實驗結論予以確定。為避免診斷結果不受初始數據隨機性的影響，診斷實驗重復50次，取平均值為結果。

4.1 數據比例分配與輸出結果描述

診斷過程中，隨機將480組樣本打亂，用于訓練、校驗、測試的樣本比例為5∶3∶2，且樣本數據間彼此不重復。由于神經網絡輸出神經元判斷類型均采用概率表示，為避免分類出現小數等特殊情況，對網絡輸出結果采取四舍五入法，直接轉換為故障類型標簽，予以識別。

4.2 ELM網絡神經元參數選擇

由于極限學習機的隱含層神經網絡數量對診斷結果存在影響，需要基于數據樣本進行實驗，選擇合適的神經元數量。訓練集、測試集診斷準確率與校驗集誤差收斂值隨極限學習機隱含層神經元數量的變化如圖8所示。

圖8 診斷準確率、校驗集收斂誤差與ELM隱含層神經元數量的關系

由圖8可知：隨著神經元數量逐漸增加，訓練集、測試集診斷準確率逐漸增加，神經元數量較少時診斷效果差，收斂誤差波動范圍較大。通過綜合分析，診斷算法中隱含層神經元數量設定為114，因為此時訓練集、測試集診斷準確率相對較高，誤差收斂值較穩定，不會出現訓練集準確率增加而測試集診斷結果降低的過擬合現象。

4.3 診斷結果描述

優化極限學習機對轉子碰摩故障的診斷結果如圖9所示。可知：在50次診斷過程中，訓練集樣本準確率為95%～98%，平均準確率高達96.8%，診斷準確率最大波動幅值為2.82%(如圖10所示)；測試集診斷準確率處于95%～95.93%，平均準確率高達95.43%，診斷準確率最大波動幅值為0.93%(如圖11所示)。在診斷過程中，算法的平均收斂誤差如圖12所示，其誤差收斂趨勢平滑下降，且能夠達到0.22的收斂精度。

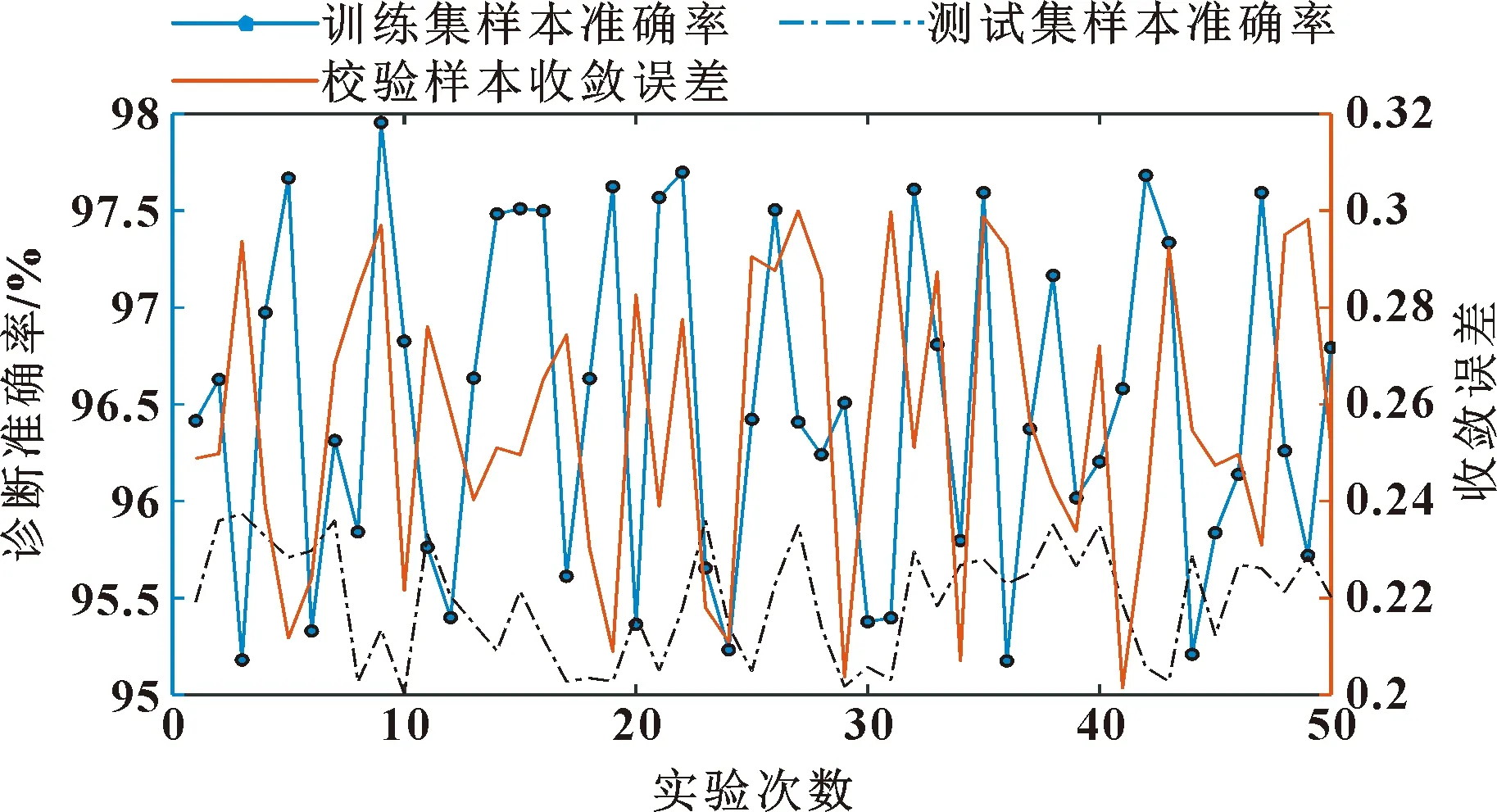
圖9 優化極限學習機50次診斷結果

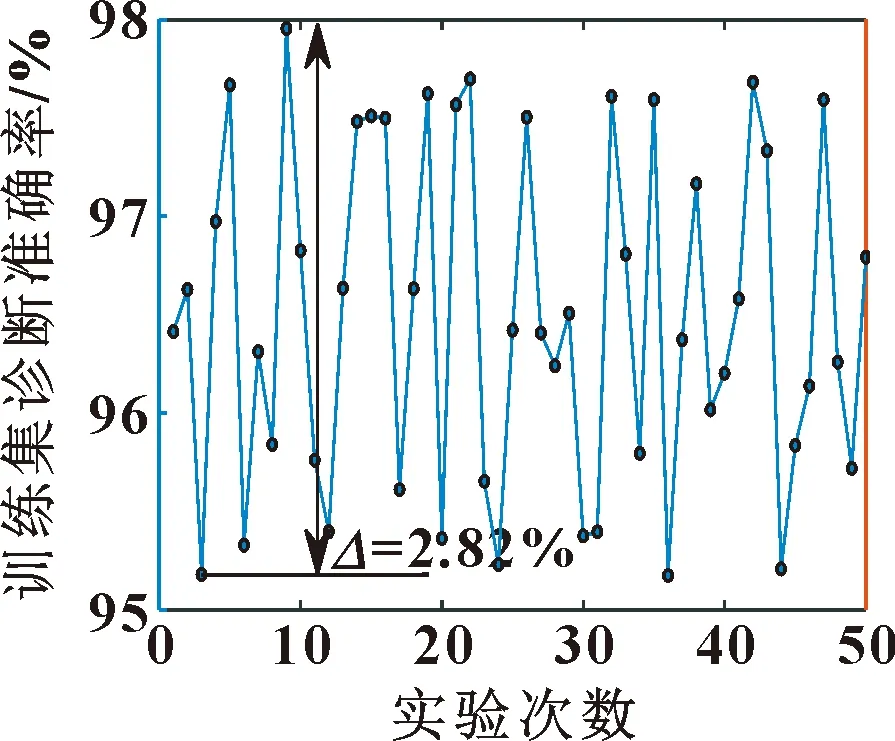
圖10 訓練集診斷結果波動情況 圖11 測試集診斷結果波動情況 圖12 校驗集平均誤差收斂情況

由上述分析可知，基于優化極限學習機的轉子碰摩故障診斷在多次診斷下，其診斷效果明顯、結果波動幅值較小，收斂誤差相對較低。因此，優化極限學習機適用于轉子碰摩故障診斷。

5 總結

針對渦軸發動機轉子出現碰摩的情況，本文作者提出了優化極限學習機的碰摩故障診斷方法。首先，基于某實際渦軸發動機振動包絡曲線，還原渦軸發動機正常狀態、燃氣渦輪碰摩、動力渦輪碰摩以及燃氣動力渦輪碰摩4種狀況下的振動信號，并對振動信號進行頻譜分析，得出不易從振動信號頻譜中識別出故障的結論；其次，提出基于振動信號特征的數據集，可使用優化的極限學習機對它進行診斷；最后，進行了仿真實驗。結果表明：優化極限學習機診斷準確高達95.43%，診斷結果波動幅值為0.93%，收斂誤差相對較低，驗證了優化極限學習機適用于轉子碰摩故障診斷。