非線性能量阱對滑動軸承-轉子系統油膜振蕩抑制效果分析

錢冰，李帥，李曉飛，李成功，馬曉棟

(1.國能大渡河檢修安裝有限公司，四川 樂山 614900；2.省部共建西北旱區生態水利國家重點實驗室，西安 710048；3.西安理工大學 水利水電學院，西安 710048)

滑動軸承-轉子系統在旋轉機械中具有無可替代的作用，在設計加工、機械制造和運行中若受到某些因素的影響會發生嚴重故障，其中常見的油膜故障包括油膜渦動和油膜振蕩。例如秦嶺發電廠、阜新發電廠和大同第二發電廠的燃氣輪機組都曾因自激振動造成振幅增大，導致不同情況的人員傷亡和機組損傷，對機組減振方面的研究十分必要。沒有固有頻率的非線性能量阱(Nonlinear Energy Sink，NES)隨系統的多階頻率振動具有較大的吸振帶寬，從而受到學者們的廣泛關注和研究。

文獻[1]采用短軸承模型研究了潤滑油在不同溫度下對系統響應的影響，發現油膜渦動轉速隨油膜溫度的升高而增大，高轉速下出現的油膜振蕩會抑制軸承的同步振動。文獻[2]基于模擬局部碰摩的故障試驗，得出振動信號中的組合頻率成分，并以此判斷碰摩發生的部位。文獻[3]對轉子系統結構特征和彎曲剛度在連接裝置處的變化進行論述，建立對應的數學模型，并發展了一種數值諧波平衡法，此方法可節省轉子動力學特性求解的時間。文獻[4]發現使用黏溫系數較大的潤滑油時，二階臨界轉速附近的轉子系統有良好的運動狀態特性。文獻[5]通過試驗發現過大的基礎振幅或頻率會導致轉子系統軸心軌跡的復雜變化和振動響應過大。文獻[6]對受基底簡諧激勵下帶有減振裝置NES的轉子系統參數進行了分析計算，發現提高NES阻尼會擴大最優剛度區域和減振頻帶。文獻[7]利用非線性的模態方法分析發現了非線性動力吸振器的穩定方法，并證明小阻尼對減振效果的影響較小。文獻[8]采用鋼絲繩隔振器的動態模型研究其阻尼特性，得到了隔振器的成分及阻尼隨振幅和頻率的變化情況。文獻[9]分析了重力和滑動摩擦對NES目標能量轉移周圍動力學的影響，結果表明重力可以實現能量轉移，提高減振效率，較大的傾角或摩擦因數會導致減振效率下降。文獻[10]研究了2個耦合非保守振子的一次線性系統的隔振特性后發現NES能夠有效吸收由瞬態寬帶干擾引起的能量。文獻[11]采用NES對雙轉子系統進行振動抑制，發現低壓轉子系統的主共振和安裝位置對減振效率有直接的影響。文獻[12]采用數值仿真驗證了吸振效果受初始能量變化的影響，并提出提高非線性吸振器性能的方法。文獻[13]通過理論與試驗結合分析，提出利用分段性彈簧的NES來增強振動抑制效果，并驗證其對振動消除效率的優越性。文獻[14]數值模擬了一種單自由度緊湊型NES與柔性材料的均勻板模型之間共振相互作用引起的被動、非線性目標能量轉移后，發現NES能夠以完全被動的方式快速、有效地吸收均勻板一個或多個模態的能量。文獻[15]研究了金屬橡膠減振器的設計方法并進行動力學建模，引入較大阻尼來降低機組的振動響應。文獻[16]設計了一種立方剛度非線性吸振器，其振動抑制效果良好。

在轉動部件振動抑制方面的研究：文獻[17-19]針對內燃機軸系振動問題，提出了一些對吸振器分岔行為、動力參數確定和結構優化的研究方法；文獻[20]利用軸瓦可調軸承在合理調節橢圓度下可以調整轉子系統的運動狀態，減弱轉子的振動；文獻[21-22]研究了在質量偏心力作用下多個NES對轉子系統振動衰減的影響，但并未深入分析NES結構參數變化時轉子的動態響應變化。因此，本文針對滑動軸承-轉子系統油膜特性問題，擬在滑動軸承處附加2個相互垂直且具有線性阻尼和非線性立方剛度的NES來對系統的大幅振動進行抑制；利用時域圖、軸心軌跡圖、龐加萊圖和分岔圖研究不同參數下的NES對轉子系統在二階臨界轉速附近，由于油膜渦動和油膜振蕩引起的轉子系統產生振動等異常現象的抑制效果。

1 數學模型

1.1 NES-滑動軸承-轉子系統模型

NES-滑動軸承-轉子系統模型如圖1所示，R為滑動軸承的內半徑，L為滑動軸承的寬度，r為軸頸半徑，l為定轉子初始間隙，O為轉子的幾何中心，Om為轉子質心，e為圓盤偏心距，c為軸頸與軸承之間的間隙，Kn為NES的立方剛度，Kb為軸承剛度，Cn，Cb分別為NES和軸承的結構阻尼。2套滑動軸承的x和y方向各有一個帶線性阻尼和非線性立方剛度的NES結構塊。

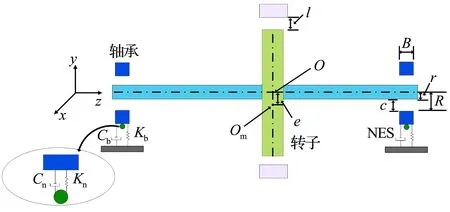
圖1 NES-滑動軸承-轉子系統模型示意圖

NES的結構如圖2所示，采用立方剛度模型(F=kx3)在滑動軸承處與轉子系統相連接。

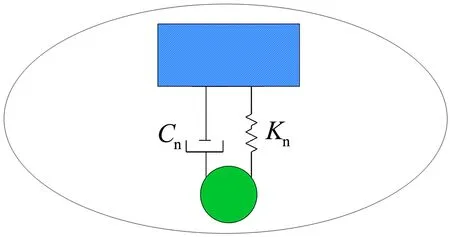
圖2 NES的結構示意圖

在模型建立和微分方程求解過程中，轉子-軸承系統轉軸兩端由滑動軸承對稱支承，不考慮轉盤的陀螺效應和扭轉振動引起的剛度變化。轉子-滑動軸承-NES系統運動的微分方程為[23]

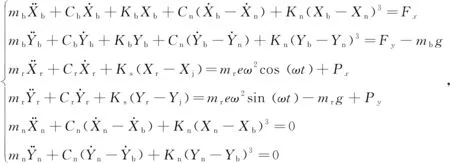
(1)

量綱一化的微分方程為

(2)

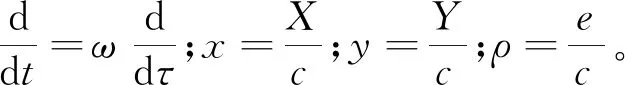
1.2 轉子的碰摩力

轉子運行過程中，當徑向振動位移超過定轉子間隙時會與定子發生碰摩，碰摩力為[24]

(3)

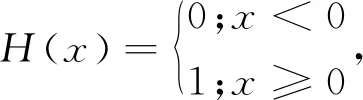
(4)

式中：H為階躍函數；Kc為定子的徑向剛度；fc為摩擦因數；δ0為定轉子間隙；X2，Y2分別為轉子在x，y方向的位移。

1.3 滑動軸承的油膜力

隨著轉軸轉動，油膜厚度和油膜壓力的變化如圖3所示。文中采用Gumbel油膜邊界條件，處于擴散區的油膜完全破裂，油壓為0。Oz，Ow分別為軸頸和軸瓦的幾何中心，φ為最小油膜厚度與x軸的夾角，p為油膜壓力，h為油膜厚度，δ為軸頸與軸瓦中心的偏心距，θ為油膜邊界任意一點與油膜最大厚度和最小厚度所處位置的夾角，轉子逆時針轉動時角速度為ω。

圖3 油膜厚度和油膜壓力變化示意圖

雷諾方程在直角坐標系下可表示為[25]

(5)

ε=δ/c，X=rθ，U=Rω，h=c(1+εcosθ)，

式中：μ為潤滑油黏度；?p/?Z為p在z方向的變化率。

應用短軸承原理，假設p在軸向的變化率要遠大于周向的變化率，且忽略滑動軸承潤滑油端泄的影響，p變化的表達式為

(6)

將軸頸受油膜壓力產生的油膜力通過在軸頸上的積分區域來計算，再轉化到x,y坐標系上，由軸頸處的受力關系可得到油膜力為關于軸頸偏心距和油膜相位角的2個強非線性關系式[22]，即

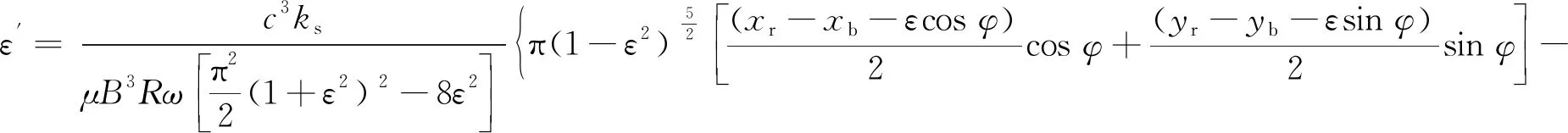
(7)

(8)

2 NES對系統振動的影響

對(2)式進行數值求解，通過NES-滑動軸承-轉子系統的相關特征圖研究NES的結構參數對系統振動減弱效果的影響，重點研究NES對系統在二階臨界轉速附近運行時發生油膜渦動和油膜振蕩的抑制作用。本文采取500～700周期的穩定解來避免瞬態擾動在初始條件時的不穩定，從而對系統的非線性現象進行分析。系統數值求解的主要參數見表1。

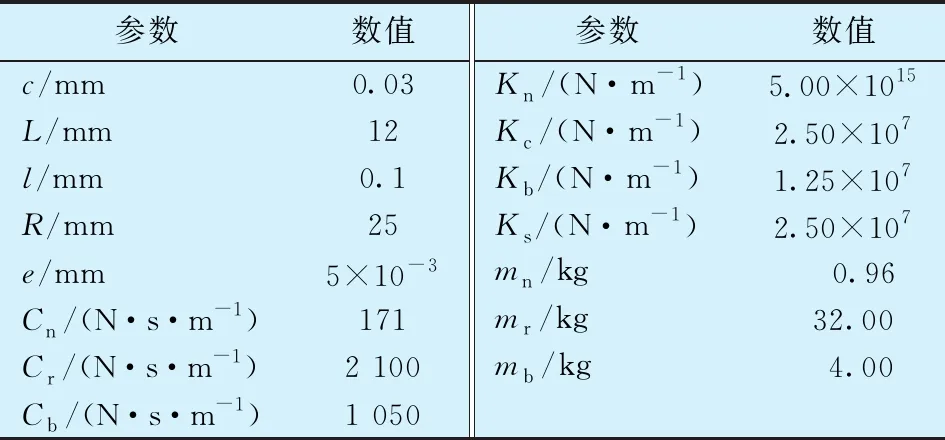
表1 NES-滑動軸承-轉子系統的主要參數

無NES時滑動軸承和轉子x方向的位移隨ω變化的分岔圖如圖4所示：當ω為0～240 rad/s時，轉子的振動位移變化較大，而滑動軸承的振動位移相對平穩；轉子的運動周期狀態及分岔點處的轉速點隨著ω的逐漸增加趨近于滑動軸承運動；當ω為240～770 rad/s時，滑動軸承-轉子系統處于一周期運動，運行較為穩定；滑動軸承-轉子系統隨著ω的繼續增加進入半分岔運動。

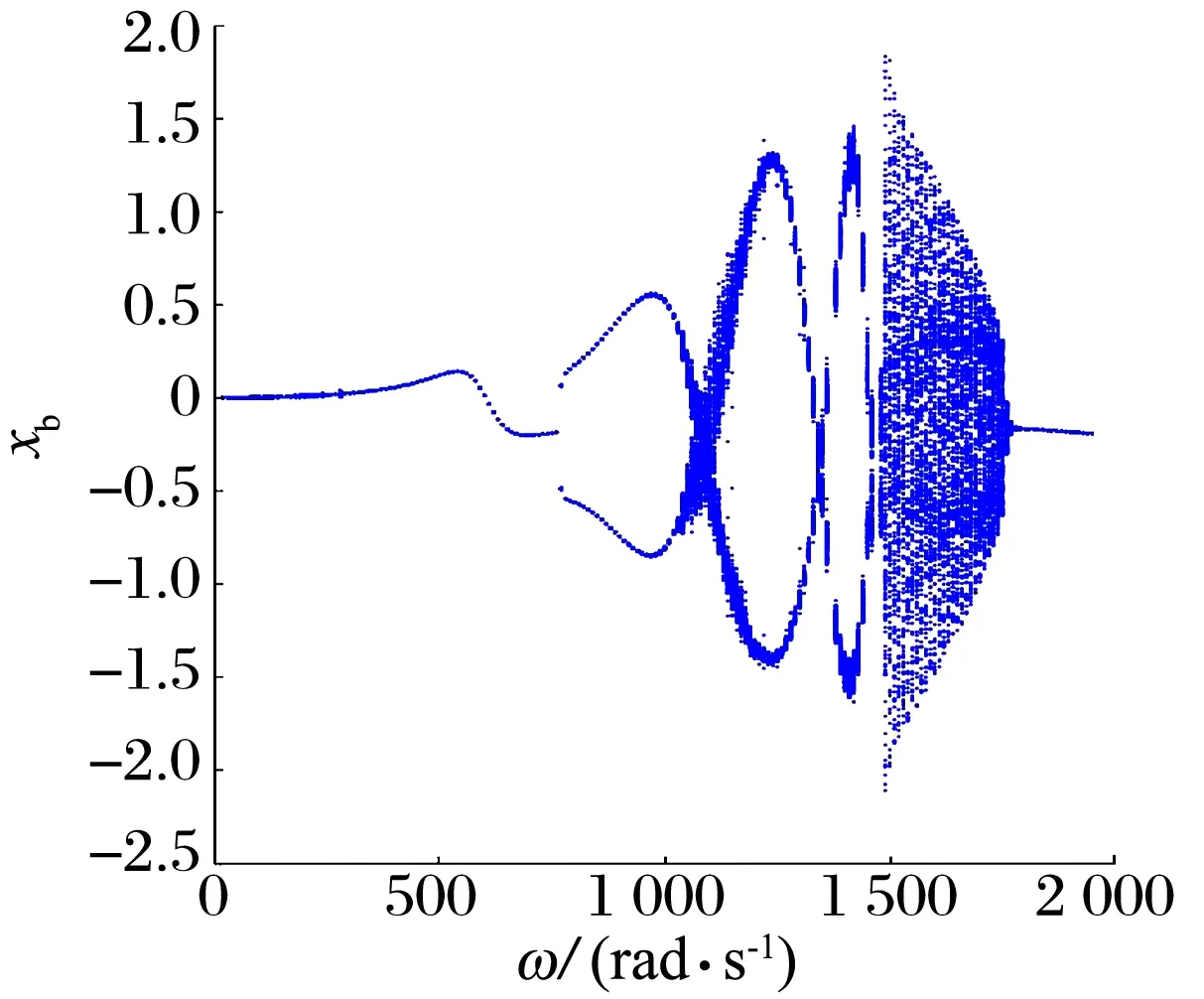
(a)滑動軸承

當ω為1 700 rad/s，無NES時轉子的運動特征如圖5所示，f為振動頻率，fr為轉動頻率，軸心軌跡圖由多條近圓狀的重疊曲線組成，龐加萊圖的散點呈花狀離散分布，頻譜圖中存在0.35，0.5和1倍頻，其中0.35倍頻占主要成分，系統呈擬周期運動。結合圖6中滑動軸承和轉子的瀑布圖可知，當ω為770 rad/s時開始出現油膜渦動現象，并且渦動幅度隨著ω的增加而持續增大，直到ω為1 360 rad/s；當ω為1 360～1 750 rad/s時以0.5倍頻為主，說明系統發生了油膜振蕩。可以看出：在高角速度區間由于碰摩和油膜失穩的作用，滑動軸承-轉子系統在ω約為1 360～1 750 rad/s時發生了混沌運動或擬周期運動。

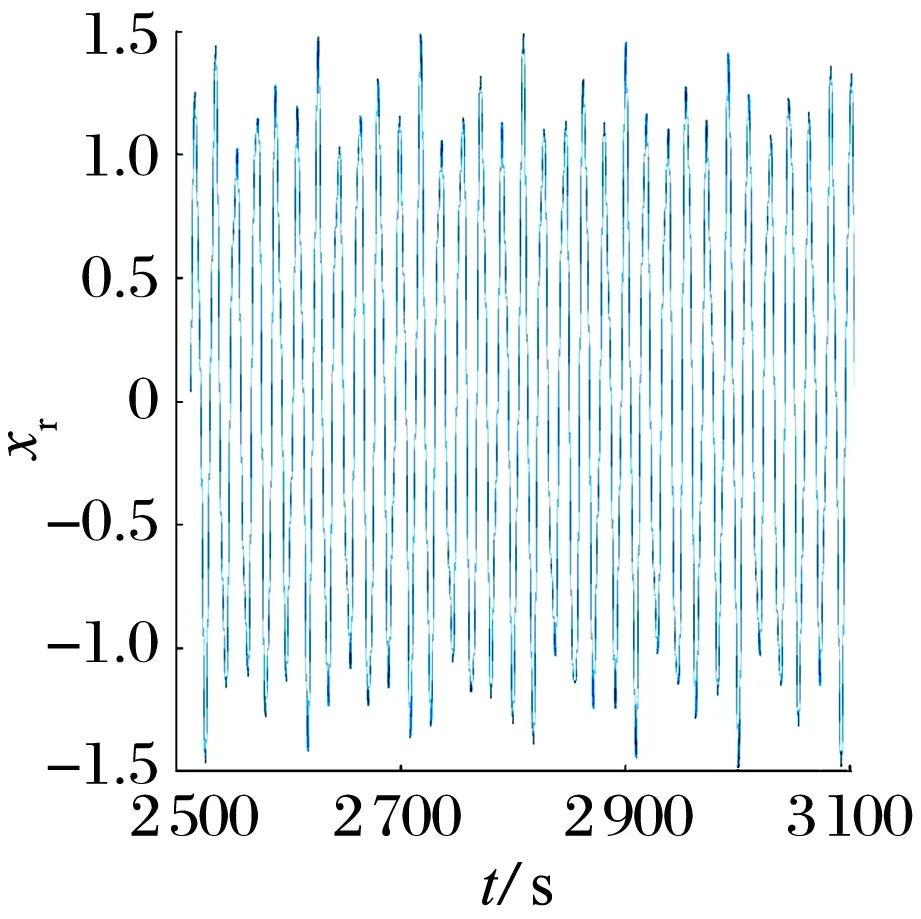
(a)時域圖

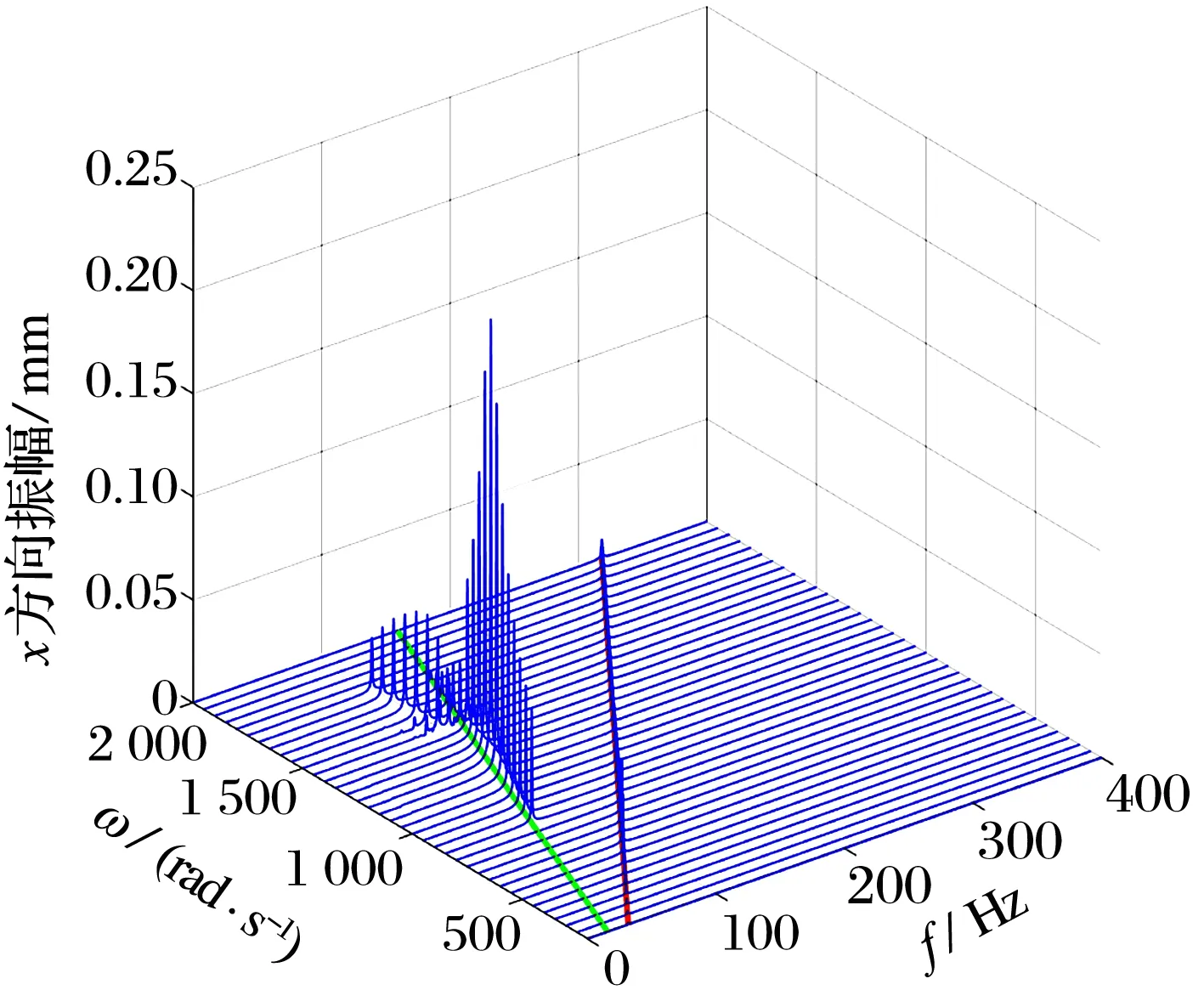
(a)滑動軸承

添加兩自由度NES時的滑動軸承和轉子x方向的位移隨ω變化的分岔圖如圖7所示。與圖4相比，附加NES的滑動軸承和轉子在ω為1 650～1 770 rad/s時x方向位移明顯減小。

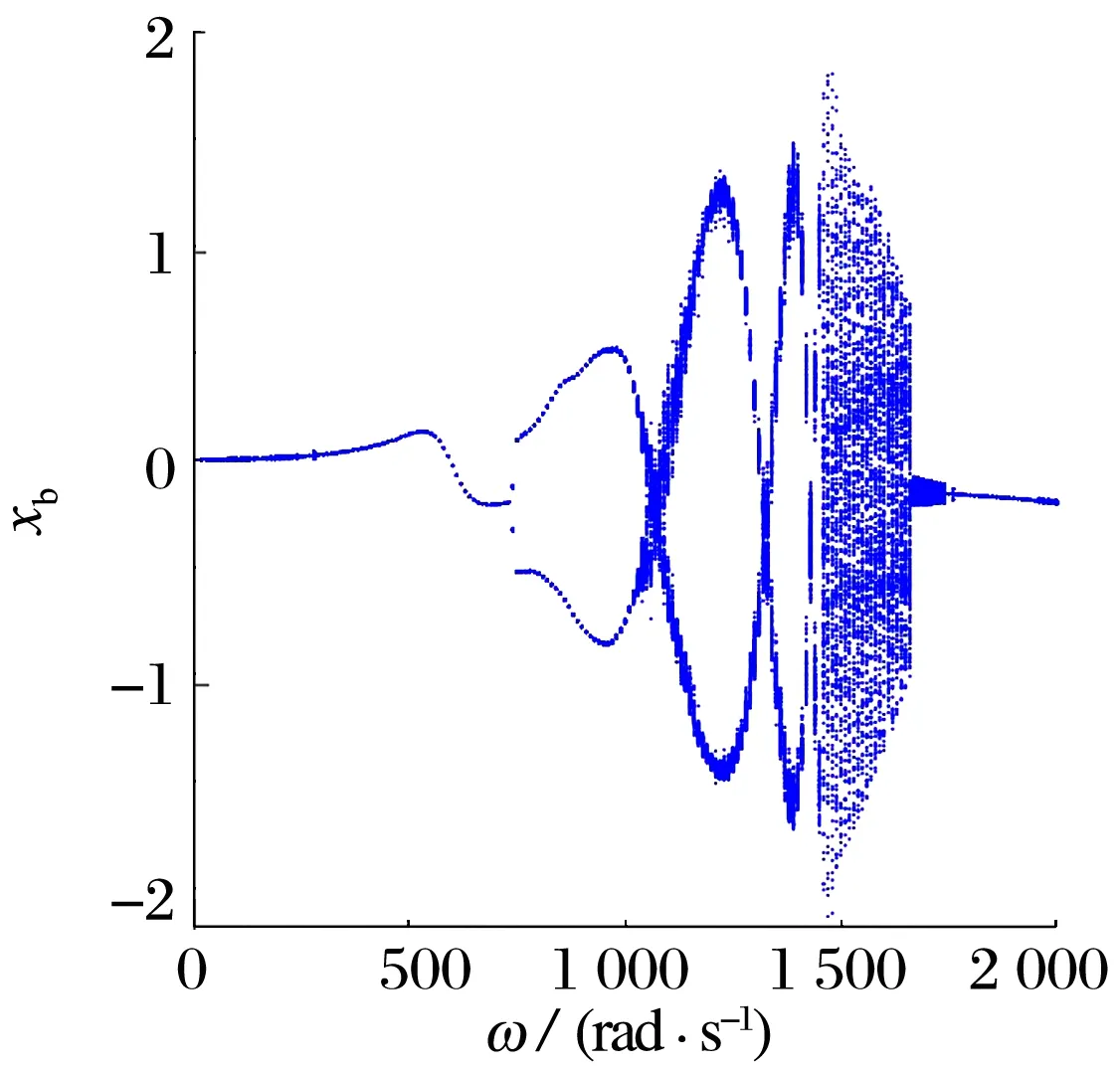
(a)滑動軸承

當ω為1 700 rad/s時，滑動軸承、轉子的運動時域圖如圖8所示，紅色、藍色曲線分別為有和無NES的x方向位移，有NES時振動位移的變化依然不規則，但NES使滑動軸承、轉子的振動位移減小了80%。

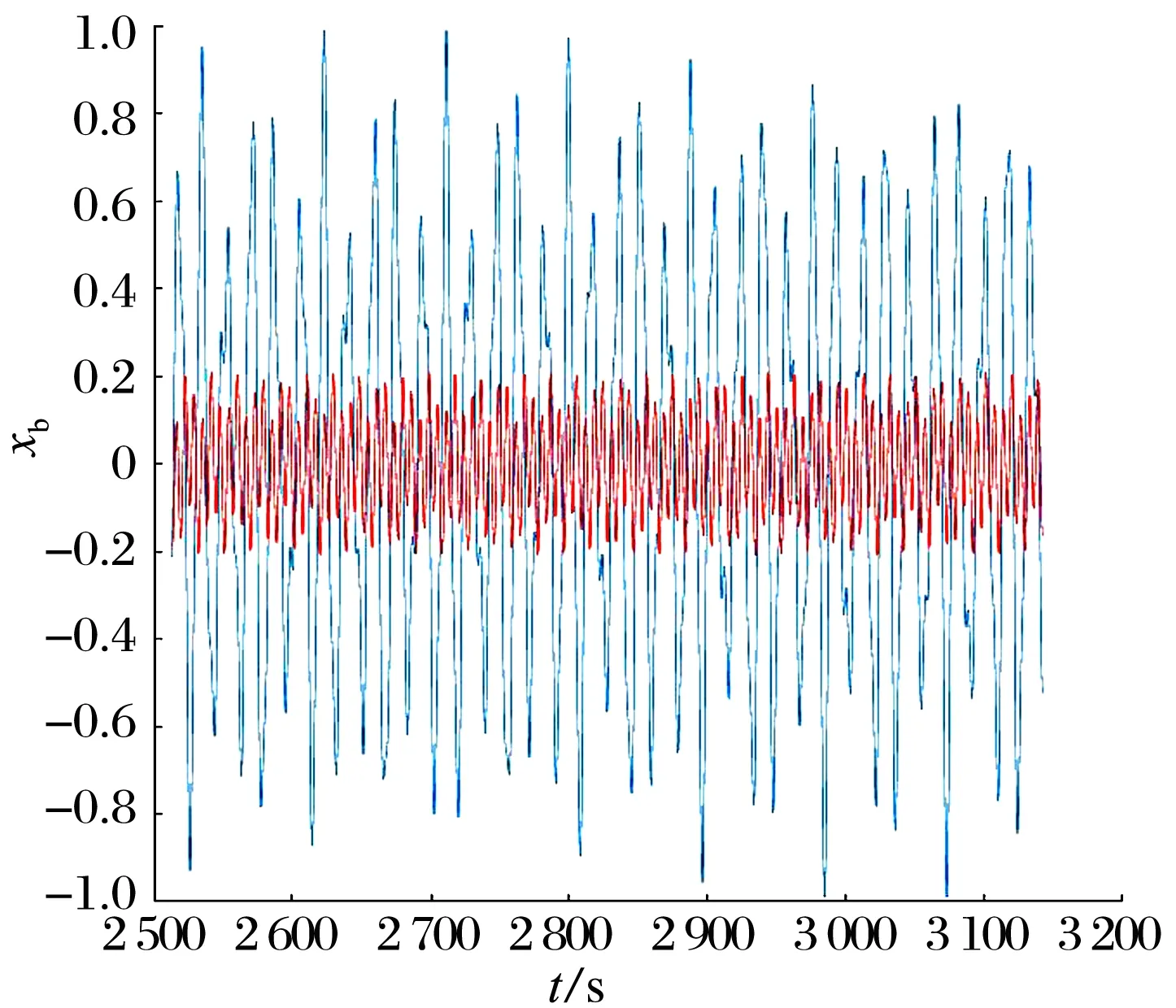
(a)滑動軸承

當轉子ω為 1 700 rad/s，添加NES時，轉子的龐加萊圖和頻譜圖如圖9所示，龐加萊圖為一條封閉的近圓狀曲線，頻譜圖中1倍頻占主導地位，但也出現了0.35倍頻，系統仍處于擬周期狀態。結合圖10中帶有減振效果NES的滑動軸承和轉子的瀑布圖，發現ω為0～1 650 rad/s時滑動軸承和轉子的運動情況與無NES的相似，說明ω為0～1 650 rad/s時添加NES對滑動軸承-轉子系統振動形態影響不大，但當ω為1 650～1 770 rad/s時能起到顯著的減振效果。

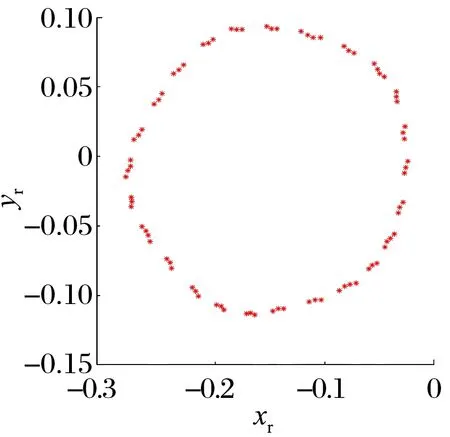
(a)龐加萊圖

(a)滑動軸承

3 NES參數對油膜振蕩的抑制效果

3.1 不同質量的NES對轉子振動特性的影響

本節研究NES的質量變化對轉子系統減振情況的影響，為了有明顯的減振效果，考慮NES的質量遠小于主結構的質量，本文NES質量在2 kg以內，轉子質量為32 kg。

當Kn為5×1015N/m，ω為1 750 rad/s，mn為0.01～2.00 kg時，轉子和NES 的y方向位移隨NES質量變化的分岔圖如圖11所示，其中當mn為0.10，1.30 kg時轉子的運動特征分別如圖12和圖13所示。由圖11a、圖12和圖13可知，當mn為0～0.35 kg時，頻譜圖中以0.35倍頻為主，轉子呈擬周期運動，轉子系統此時開始出現油膜渦動；當mn為0.35～0.98 kg時，隨著mn的增大，轉子振動位移顯著減小，一直處于穩定的一周期運動；當mn>1.00 kg時，轉子呈擬周期運動：說明mn只在某一段特定范圍內會對轉子的運動起到明顯的減振作用，從而達到一種能量俘獲效果。

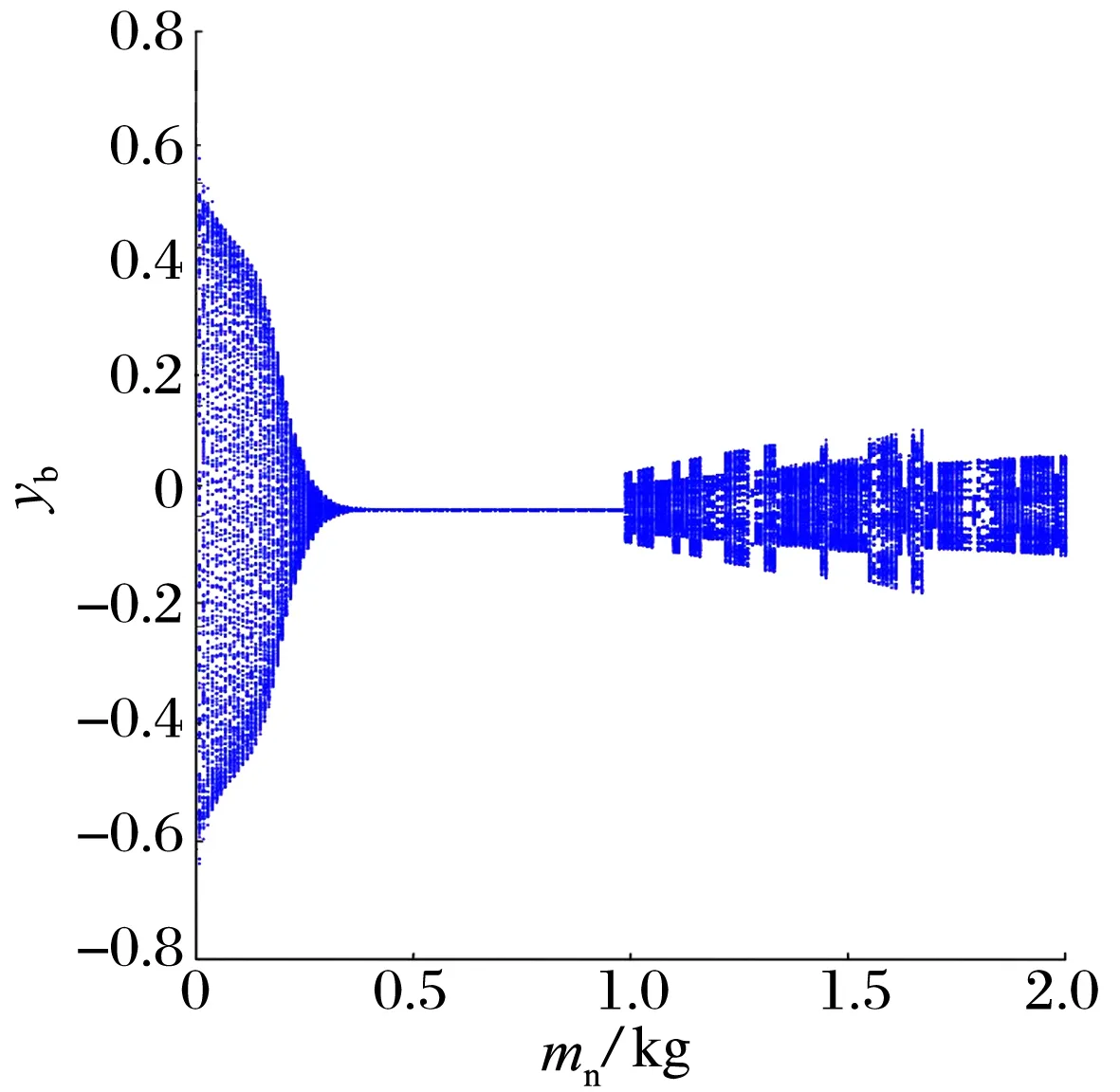
(a)轉子

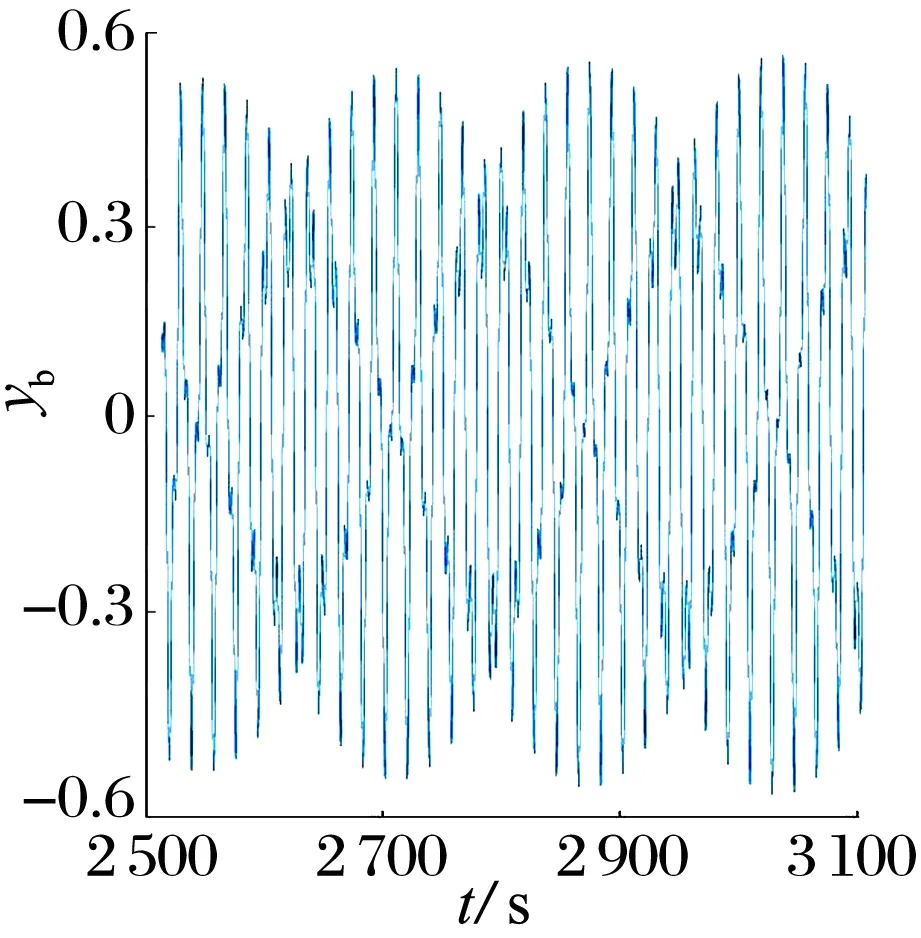
(a)時域圖

(a)時域圖

3.2 不同立方剛度的NES對轉子振動特性的影響

當NES質量為0.96 kg，ω為1 750 rad/s時，轉子y方向的位移隨Kn變化的分岔圖如14所示：當Kn為0～3.60×1015N/m時，隨著Kn的增加，轉子的振動位移逐漸減小；當Kn為(3.60～6.67)×1015N/m時，隨著Kn的增加，轉子的振動位移波動較大；在Kn達到6.67×1015N/m后，轉子的振動位移減小至零，NES對轉子的減振效果達到最優。

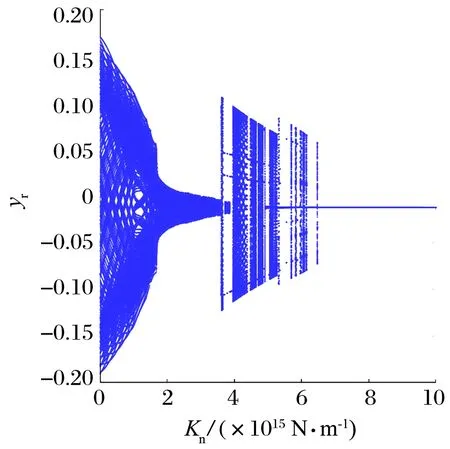
圖14 轉子的位移隨NES立方剛度的變化

3.3 NES阻尼變化對轉子系統運動的影響

當NES質量為0.96 kg，ω為1 750 rad/s，添加 NES時，轉子y方向的位移隨NES阻尼變化的分岔圖如15所示：當Cn=171 N·m/s時，轉子振動位移大幅下降，之后轉子表現出穩定的一周期運動。說明當Cn為0～170 N·m/s時，轉子y方向的位移一直處于混沌或擬周期狀態，當阻尼大于171 N·m/s時轉子系統才會有比較明顯的振動減弱效果。

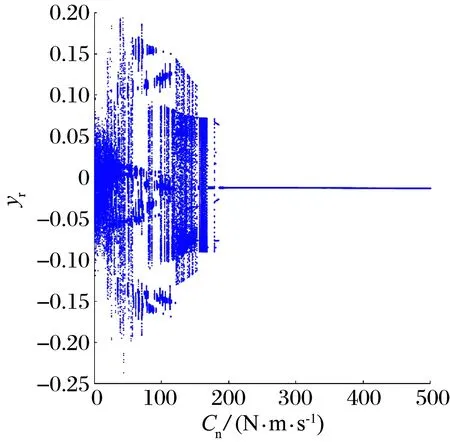
圖15 添加NES時轉子的位移隨NES阻尼的變化

當NES質量為0.96 kg，ω為1 750 rad/s，Cn為0，添加 NES時，轉子的運動特征如圖16所示，時域圖中y方向的振動位移比較雜亂，軸心軌跡圖為數量較多且不重疊的橢圓運動軌跡，龐加萊圖中點的分布雜亂無規律，頻譜圖中以0.35，1倍頻為主，說明轉子此時處于混沌狀態：即添加NES時轉子運動不穩定，對系統振動起到了消極作用。

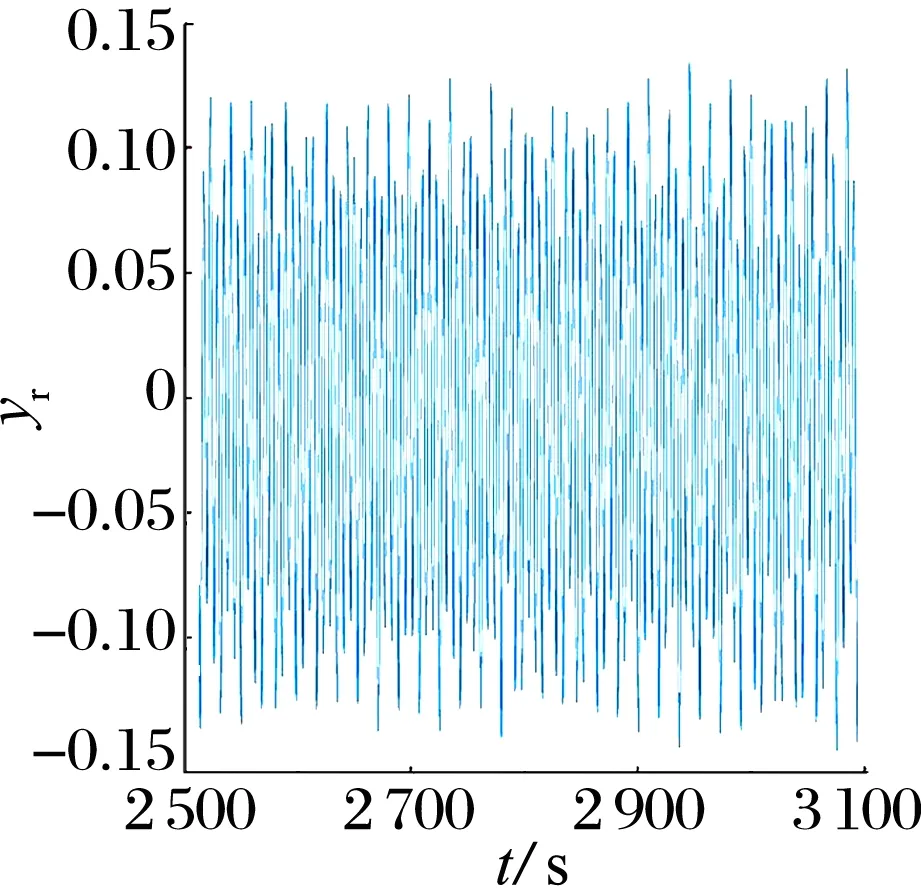
(a)時域圖

4 結論

建立了添加NES的滑動軸承-轉子系統的動力學模型，研究不同結構質量、立方剛度和線性阻尼對系統減振效果的影響，得到如下結論：

1)當ω為1 650～1 770 rad/s時，NES對系統運動起到顯著減振效果。

2)當mn為0.35～0.98 kg時，隨著mn的增大轉子的振動位移顯著減小；當Kn達到6.67×1015N/m后，轉子的振動位移減小至零，NES對轉子的減振效果達到最優；超過此范圍后參數的改變對系統振動特性無明顯影響。

3)NES的結構阻尼不宜過小，在結構阻尼大于171 N·m/s時，系統油膜失穩引起的大幅振動可以得到很好的抑制，即NES的結構阻尼增加至某一閾值時滑動軸承-轉子系統才會有明顯的振動衰減效果。