預設性能控制的脆弱性問題探究
卜祥偉,姜寶續
(1.空軍工程大學防空反導學院,西安,710051;2.空軍工程大學研究生院,西安,710051)
自動控制技術使人類從繁重的體力勞動中解放出來,實現了從“手動”到“自動”的巨大跨越[1-2]。自動控制技術也是當今世界發展最快,影響最深遠的技術之一。自動控制系統設計的核心是通過尋找合適的反饋控制律,使得閉環控制系統的輸出定量或定性地滿足“穩”“準”“快”等方面的性能指標要求。對于能控且能觀的線性定常系統,總能找到合適的反饋控制律,對閉環系統的極點進行任意配置,從而對控制系統的性能指標進行任意地定量設計。然而,對于非線性系統,傳統基于Lyapunov理論的反饋控制策略,通常僅能將穩態誤差最終或在有限時間內調節到一個大小可調的緊集內,以實現對穩態性能的定性設計,但卻無法對收斂時間、超調量等動態性能指標進行定量或定性設計[3]。
至于如何保證非線性控制系統同時具備滿意的動態性能與穩態精度,IEEE Fellow、加拿大Davison教授早在1991年就進行了初步探索[4]。之后,德國學者Ilchmann等人[5]于2002年創立了漏斗控制(funnel control, FC)理論,謀求通過設計不依賴系統模型的高增益控制律來保證控制誤差期望的動態性能與穩態精度。但是,由于限制條件太過苛刻,FC僅適用于極少數的一類特殊系統[5-6]。為此,在FC的基礎上,希臘學者Bechlioulis等人又于2008年演化發展出了預設性能控制(prescribed performance control, PPC)理論[7]。PPC基于“性能函數設計”與“誤差等價變換”的基本框架,可與現存幾乎所有的控制理論相結合,從而設計出多種多樣的控制律形式,將控制誤差始終限定在預設的約束包絡內,以便同時保證控制誤差期望的動態性能與穩態精度。因此,近年來PPC已經成為控制領域的一個前沿熱點方向,引起了國內外科技人員的格外關注。
1 PPC概述
PPC突破了傳統控制理論無法約束控制系統動態性能的限制,實現了對控制系統動態性能的約束與調節,在保證理想控制精度的同時,兼顧超調量與調節時間等動態性能,可以保證控制系統具有較好的過渡品質。所謂預設性能是指將跟蹤誤差限定在一個預先設定的可調區域內,以保證跟蹤誤差收斂過程的動態性能與穩態性能滿足預先設定的要求[7]。PPC的基本思想是設計性能函數ρ(t)∈R>0對跟蹤誤差e(t)的收斂軌跡進行限定,通過為ρ(t)選擇特定的設計參數來保證e(t)具有滿意的動態性能與穩態精度,見圖1。
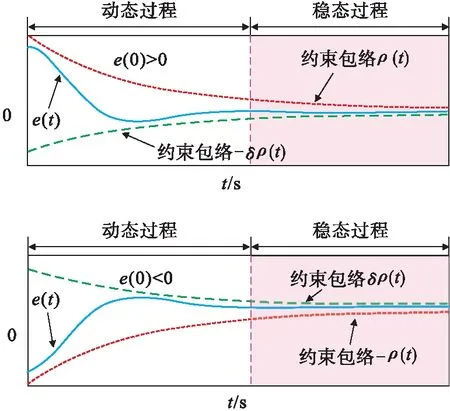
圖1 PPC對誤差e(t)的包絡約束示意圖
1.1 性能函數
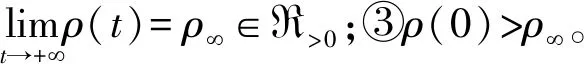
文獻[7]將ρ(t)設計為ρ(t)=(ρ0-ρ∞)e-lt+ρ∞,這里,ρ0>ρ∞>0,l∈R>0為待設計參數。
如果誤差初值e(0)為已知,則采用ρ(t)對e(t)進行如下包絡約束:
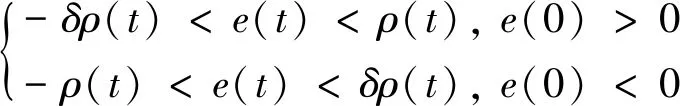
(1)
0≤δ≤1為待設計參數,由于工程實際中e(0)=0的情況很少見,文獻[7]中未考慮。
注1:以0<|e(0)|<ρ(0)為例,則ρ∞表示e(t)穩態值的上界,δρ(0)表示e(t)允許的最大超調,ρ(t)的收斂速度直接影響e(t)的調節時間。因此,若能將e(t)限定在圖1與式(1)所示的區域內,就可通過為ρ(t)選擇合適的設計參數,來保證e(t)具有滿意的動態性能與穩態精度。
1.2 誤差變換
由于無法直接針對式(1)設計控制律,故引入誤差變換函數S(ε(t)),將受約束系統(1)轉化為如下不受約束的等價系統:
e(t)=ρ(t)S(ε(t))
(2)
式中:ε(t)∈R為轉換誤差,S(ε(t))的表達式為:
(3)
式(3)的逆變換為:
(4)
引理1[7]:如果轉換誤差ε(t)有界,則預設性能(1)可達,即對于任意e(0)滿足式(1),則跟蹤誤差e(t)始終位于預設的約束包絡(1)內。
實際的控制律是基于式(4)設計的,且控制律設計用到的是轉換誤差ε(t)而非跟蹤誤差e(t)。引理1表明,只要轉換誤差ε(t)有界,便能保證e(t)具有期望的動態性能與穩態精度。
2 PPC的脆弱性缺陷
近年來,PPC理論得到了快速發展,取得了一大批可喜的研究成果[8-10]。研究者們注意到Bechlioulis[7]的約束包絡(1)需要根據e(0)的符號分情況進行構造,由此導致控制律也要根據e(0)的正、負情況重復進行設計,這其中可能還要涉及不同情形的控制切換問題。這種對e(0)的依賴問題嚴重制約了其工程實用性。為此,文獻[11~12]設計了一種新型性能函數,通過設定一個充分大的性能函數初值,使PPC擺脫了對誤差初值的依賴,在一定程度了增強了算法的可操作性。但是,過大的性能函數初值極易造成超調量失控,導致跟蹤誤差的動態性能不理想。為了克服這個缺陷,文獻[13~14]利用符號函數的性質,將傳統性能函數[7]改進為一種能夠保證跟蹤誤差小超調收斂的新型約束形式;相關仿真結果表明,該方法可以保證跟蹤誤差小超調甚至無超調收斂。傳統PPC約束包絡[8-14]的收斂時間需要綜合利用性能函數的所有設計參數才能定性地確定一個大致的范圍,因此很難對跟蹤誤差的收斂時間進行定量約束。為此,文獻[15~16]在充分借鑒有限時間滑模控制相關思想的基礎上,設計了有限/固定時間性能函數,保證了跟蹤誤差在任意設定的時間內收斂到穩態。上述PPC方法僅能定性地或部分定量地保證跟蹤誤差期望的預設性能,鑒于此,文獻[17]將小超調PPC與有限時間PPC相結合,為乘波體飛行器提出了一種定量PPC新方法,能夠保證跟蹤誤差具有任意設定的收斂時間和穩態誤差,并且超調量近似為零。除此之外,PPC在輸入受限系統[18-19]與受擾系統[19-20]也有較多應用。但是,應當特別指出的是,現有PPC在處理控制執行器飽和、受擾等問題時,極易誘發控制奇異問題,表現出十分明顯的脆弱性缺陷。所謂脆弱性[21-22],是指當控制執行器突發飽和或受擾時,即便采取及時有效的補償措施,控制誤差相對于飽和與擾動出現之前也會有明顯的瞬時增加[19,21-22];當控制誤差因增大而逐漸接近甚至越過約束包絡時,就會導致控制奇異、閉環系統失穩進而控制失效、預設性能不可達,見圖2。
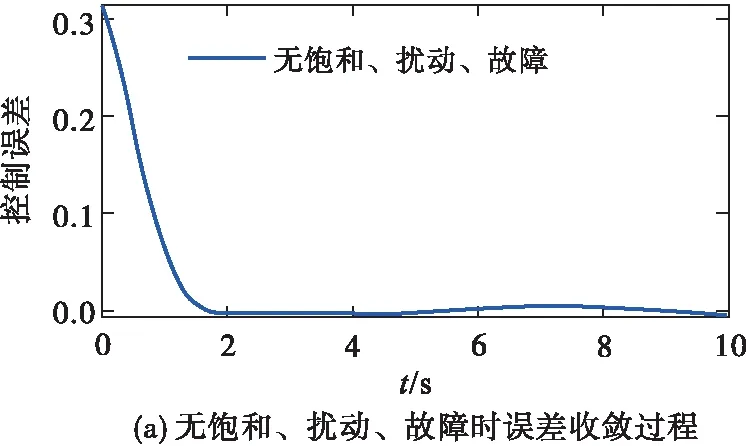
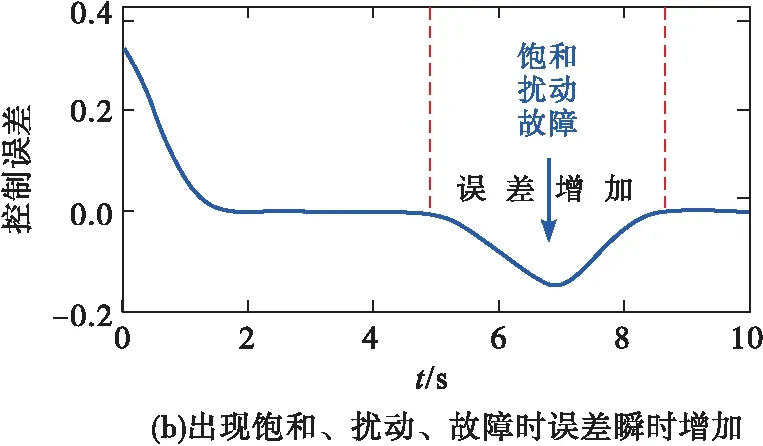
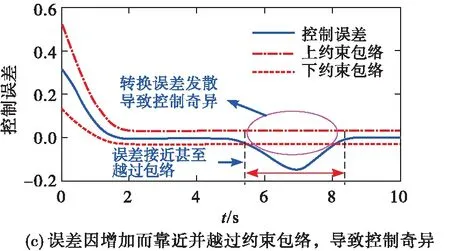
圖2 PPC的脆弱性示意圖
以執行器飽和為例,分析PPC的脆弱性成因。PPC以轉換誤差ε(t)作為反饋變量,構造反饋控制律u(ε(t)),將跟蹤誤差e(t)限定在式(1)所示的約束包絡內。將執行器飽和定義為:
(5)

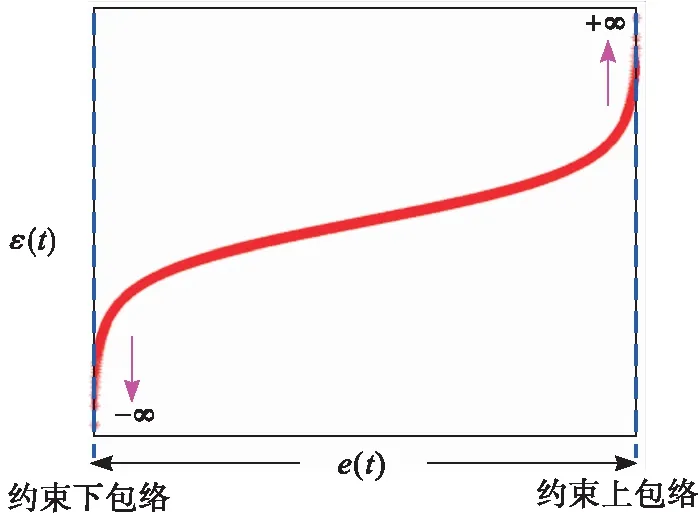
圖3 e(t)靠近束包絡時ε(t)變化示意圖
盡管文獻[18~20,23~24]的PPC方法也涉及執行器飽和與外部擾動等問題,仿真結果似乎表明方法依然有效。但是,應當清楚看到,上述方法僅考慮極短時間內的執行器飽和或較平緩的外部擾動,飽和與擾動還尚未引起足夠明顯的誤差波動,故未能呈現出PPC的脆弱性缺陷。考慮到幾乎所有的控制系統都或多或少存在執行器飽和與受擾等問題,PPC的脆弱性缺陷已經成為制約其理論發展與工程應用的技術瓶頸,是PPC走向工程實用所必須邁過的“鴻溝”。因此,探索非脆弱PPC新理論已經迫在眉睫。
3 非脆弱PPC新理論基本構想
由PPC脆弱性成因分析可見,執行器飽和、受擾等因素導致PPC控制奇異的一個關鍵原因是傳統的預設約束包絡不具備再調整能力,即預設約束包絡不能實時“感知”由執行器飽和與受擾等因素引起的誤差波動情況,也不能根據誤差e(t)的波動情況,有針對性地自動調整預設約束包絡,導致誤差因接近甚至到達預設約束的上、下包絡而造成控制奇異,見圖2(c)。
基于以上分析,給出非脆弱PPC新理論的基本構想。所謂非脆弱PPC,是指預設約束包絡能夠自主感知誤差波動,自動調整約束包絡,從而確保控制執行器飽和、受擾等情形下預設性能始終可達的PPC新理論[9,21-22],見圖4。為了達成非脆弱PPC的上述設想,需要突破誤差感知、包絡調整與預設可達等一系列的基礎性問題。
3.1 誤差感知
誤差感知,是指PPC能夠實時“感知”跟蹤誤差的波動態勢,即確定跟蹤誤差是否存在靠近約束上包絡或下包絡從而導致控制奇異的風險隱患。為了確保能夠準確感知誤差波動情況,需要事先剖析控制執行器飽和、受擾等引起誤差波動的根本原因,進而探究約束包絡對誤差波動的自主感知模式,從而構建的自主感知方案。
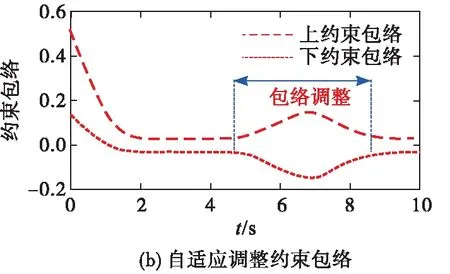
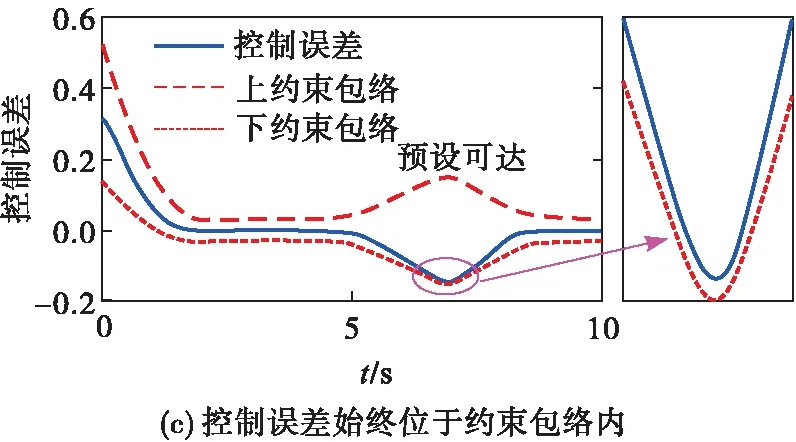
圖4 非脆弱PPC關鍵技術構想示意圖
3.2 包絡調整
包絡調整,是指在準確感知誤差波動態勢的基礎上,PPC能夠自動調整預設約束包絡的形狀(比如,當“感知”到誤差增大時,可以自適應地增大約束上包絡,減小約束下包絡,以避免控制奇異),以保證跟蹤誤差始終位于約束包絡內。為了達成這個目標,需要針對控制執行器飽和、受擾等導致的誤差波動問題,分類研究和制定約束包絡的調整方案。還要尋找導致誤差波動的關鍵變量,探索約束包絡調整項的構造方法。
3.3 預設可達
預設可達,是指在預設約束包絡再調整的情形下,將跟蹤誤差約束在約束包絡內應當滿足的相關條件。為了避免飽和、擾動等導致的PPC奇異問題,需要在準確感知誤差波動的基礎上,設計調整項對約束包絡(由性能函數構造)進行修正,修正以后的性能函數不再滿足傳統PPC中必須為連續單調遞減的限制條件。對于這種跳出現有PPC理論框架之外的特殊情形,還需要研究采用何種補償措施、構建何種反饋控制方案,才能保證閉環系統穩定和轉換誤差有界,從而保證預設性能是可達的。
4 非脆弱PPC應用案例
根據非脆弱PPC新理論的上述構想,基于筆者的前期成果[24],給出非脆弱PPC可行的技術方案。
4.1 受擾動力學系統的非脆弱PPC方案
考慮如下受擾動力學系統
(6)
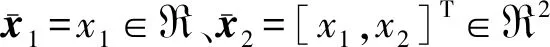
控制目標為:設計虛擬控制律x2d與實際控制律u,使得x1跟蹤其參考指令x1d,x2跟蹤x2d,并且跟蹤誤差e1=x1-x1d、e2=x2-x2d滿足如下預設性能[24]:
(7)
式中:
Pl1=[sign(e1(0))-0.5]ρ1-0.3sign(e1(0));
Pr1=[sign(e1(0))+0.5]ρ1-0.3sign(e1(0));
Pl2=[sign(e2(0))-0.5]ρ2-0.15sign(e2(0));
Pr2=[sign(e2(0))+0.5]ρ2-0.15sign(e2(0));
ρ1=(2.5-0.3)exp(-0.4t)+0.3;
ρ2=(2.5-0.15)exp(-0.4t)+0.15。
轉換誤差為[24]:
(8)
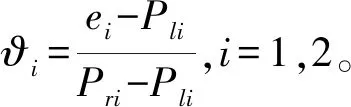
鑒于文獻[24]的傳統PPC不具備約束包絡自調整能力,當遭遇足夠強度外部擾動d1(t)、d2(t)時,極易造成控制奇異,表現出明顯的脆弱性缺陷。為此,基于前文非脆弱PPC新理論的相關構想,對文獻[24]方法進行改進,給出一種非脆弱PPC的可行方案。
對文獻[24]的預設性能式(7)進行改進:
(9)
式中:Re,1(t)∈R≥0、Re,2(t)∈R≥0為自適應調整項,
Re,i(t)公式表示如下,式中τ1,e,i=5,τ2,e,i=1/3,i=1,2。
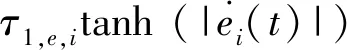
基于非脆弱預設性能(式(9)),對轉換誤差(式(8))修正,見式(10):
(10)
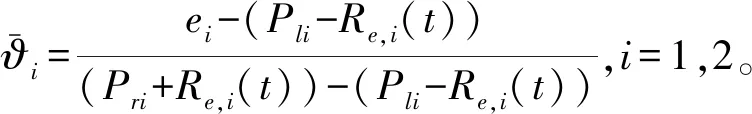
閉環控制系統的穩定性證明過程見文獻[24],文中不再贅述。
4.2 輸入受限動力學系統的非脆弱PPC方案
考慮如下輸入受限的倒立擺系統[25]:
(11)
式中:mc=1 kg,m=0.1 kg,l=0.5 m,g=9.8 m/s2。
假設u∈R受到如下飽和約束:
(12)
式中:ud為u的期望值,um與uM分別為u的下界與上界。
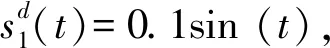
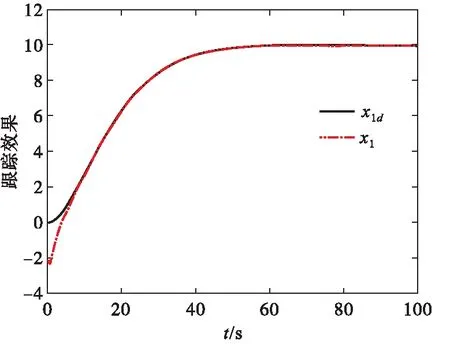
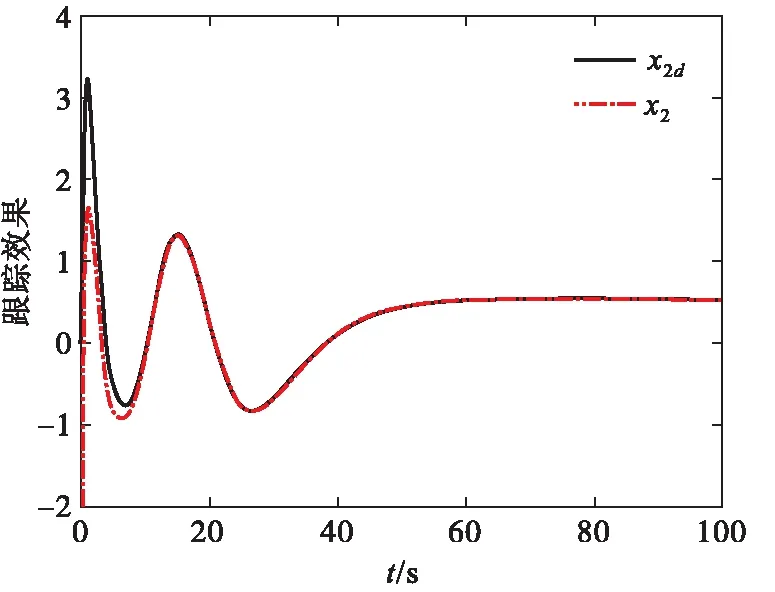
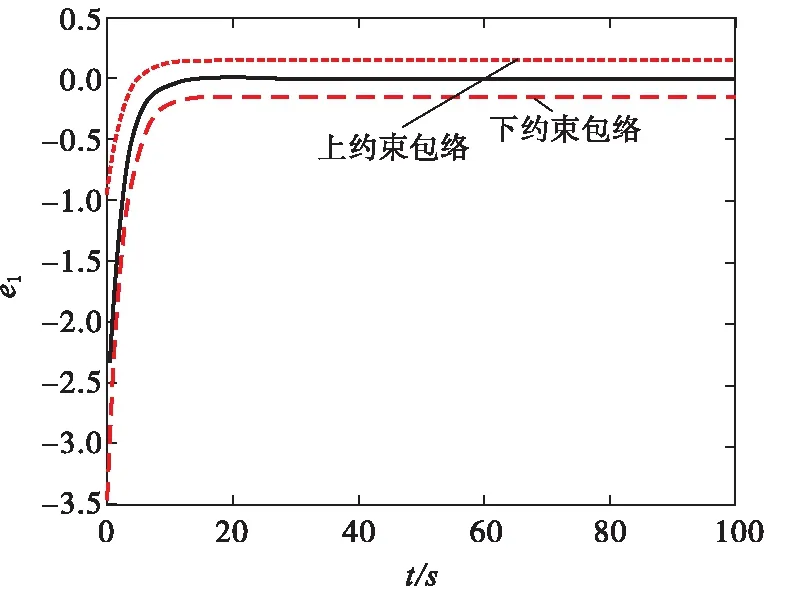
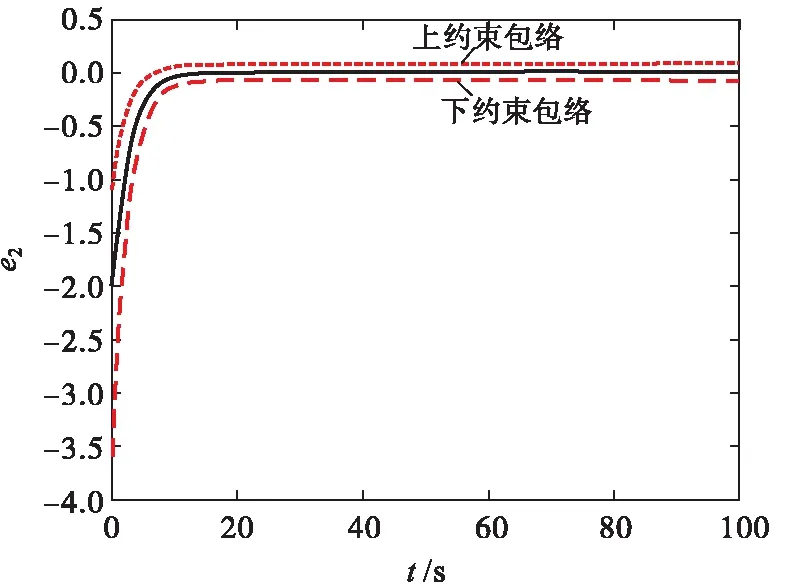
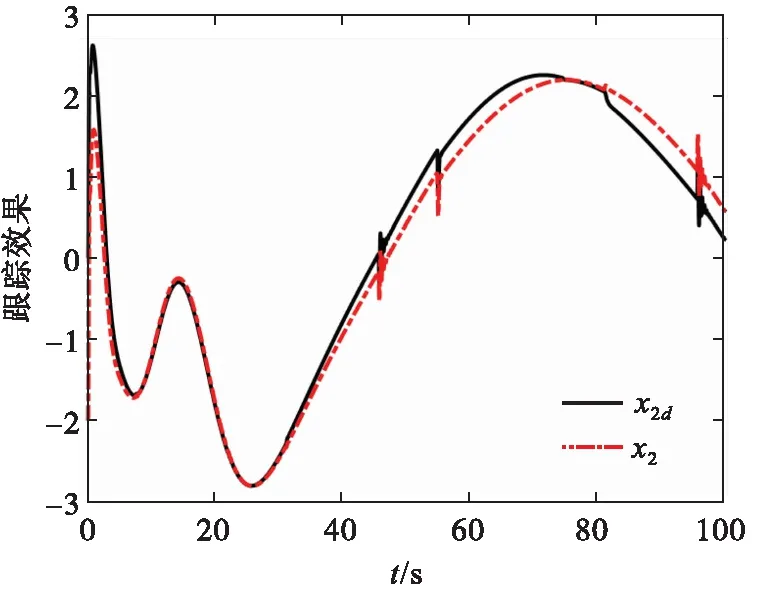
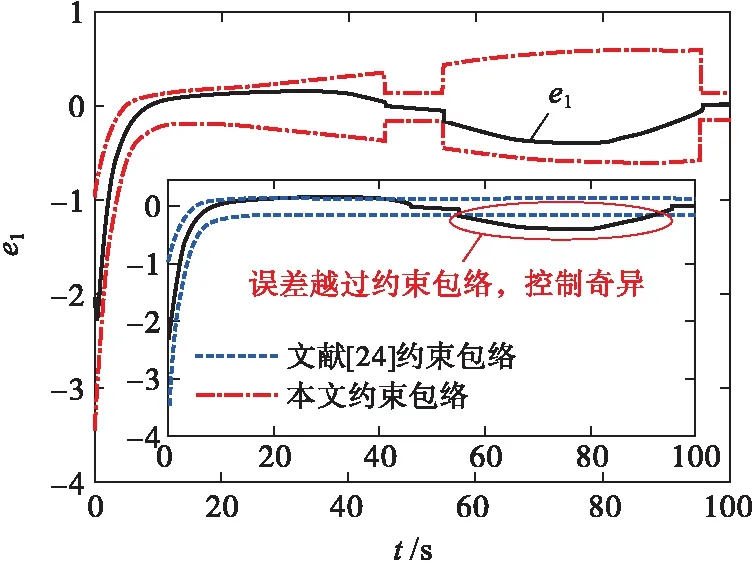
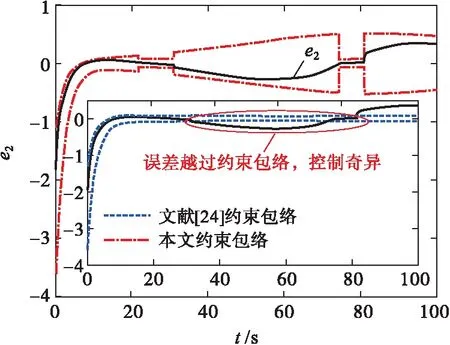
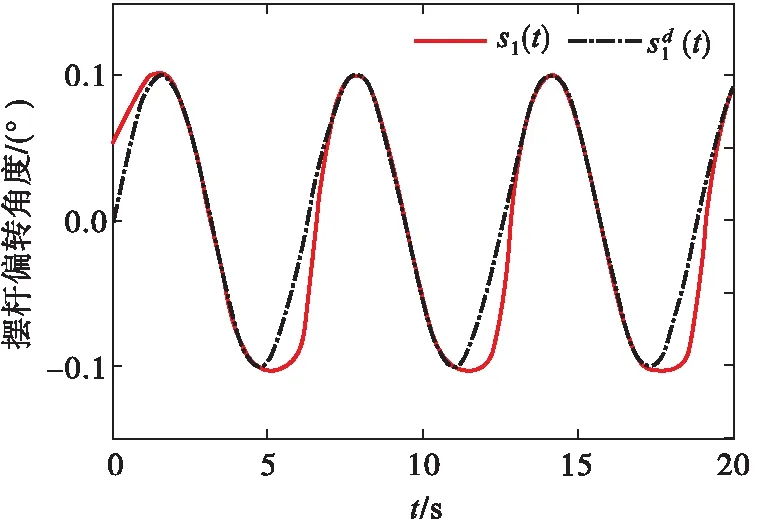
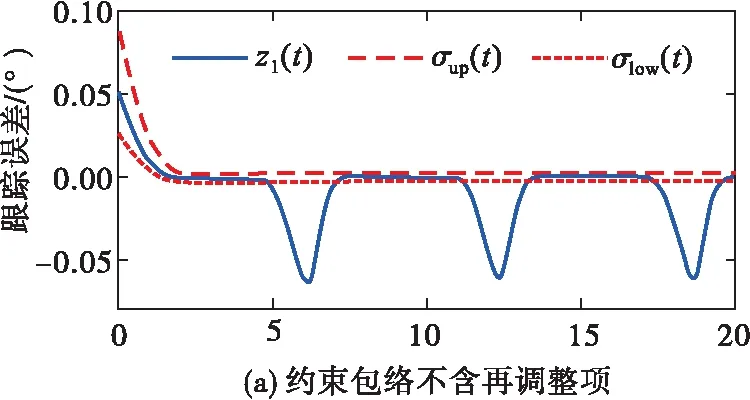
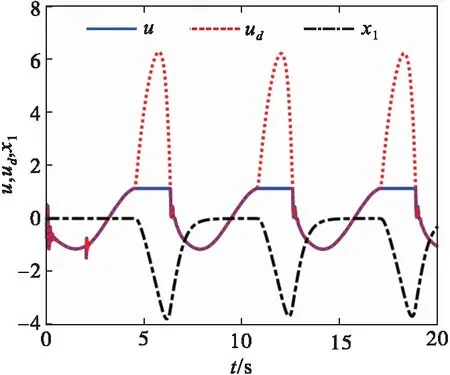
σlow(t)-φr (13) 式中: φr=c2tanh (abs(c1,1x1)) 其中,α=2,T=2,p0=π/50,pT=π/600,c2=0.2,c1,1=0.1;x1為如下輔助系統的狀態: (14) 式中:Λ1(x1)=(ex1-1)/(ex1+1);a1=5。 定義轉換誤差Tz∈R: (15) 為s2(t)選取如下參考指令: (16) 式中:kT=1.5。 (17) 式中:kz=2。 注3:針對輸入受限問題,所設計的非脆弱預設約束包絡(13)含有一個自適應調整項φr∈R≥0。以x1作為感知變量,當執行器處于飽和時,有x1≠ 0,φr=c2tanh (|c1,1x1|)>0。則φr能夠準確感知控制輸入的飽和情況,并自適應地增大約束上包絡并減小約束下包絡(調整幅值為c2tanh (|c1,1x1|)),從而確保跟蹤誤差始終位于約束包絡內,保證了預設性能的可達性,并克服了傳統PPC的脆弱性缺陷。 為了驗證非脆弱PPC相對于傳統PPC的優越性,采用MATLAB/Simulink軟件進行數字仿真,采用四階龍格-庫塔法進行求解,仿真步長均為0.01 s。 分別在以下兩種情景下進行仿真。 情景1:采用文獻[24]的PPC進行仿真,且不考慮外部擾動,仿真結果如圖5~8所示。 情景2:采用本文的非脆弱PPC進行仿真,且考慮外部擾動,并取d1(t)=2sin(0.02πt)、d2(t)= 2sin(0.02πt),仿真結果如圖9~12所示。 圖5 x1對其參考指令的跟蹤效果(情景1) 圖6 x2對其參考指令的跟蹤效果(情景1) 圖7 跟蹤誤差e1(情景1) 圖8 跟蹤誤差e2(情景1) 圖9 x1對其參考指令的跟蹤效果(情景2) 圖10 x2對其參考指令的跟蹤效果(情景2) 圖11 跟蹤誤差e1(情景2) 圖12 跟蹤誤差e2(情景2) 由圖5~8可見,當沒有外部擾動時,文獻[24]的傳統PPC能夠實現x1、x2對其參考指令的精確跟蹤,并且,跟蹤誤差e1、e2始終位于約束包絡(7)內,具有滿意的動態性能與穩態精度。但是,圖11~12表明,當存在外部擾動時,文獻[24]的傳統PPC無法將e1、e2限定在約束包絡(7)內,將直接導致控制奇異,表現出明顯的脆弱性。圖9~12表明,即便存在外部干擾,所提出的非脆弱PPC仍能有效避免控制奇異問題。當外部擾動導致跟蹤誤差增加時,所提出的非脆弱PPC能夠自主感知誤差的變化趨勢,并自動調整約束包絡(9),即增大上包絡同時減小下包絡,使得跟蹤誤差始終位于約束包絡(9)內,滿足期望的預設性能。綜上所述,仿真結果充分證明了本文非脆弱PPC的有效性以及相對于傳統方法的優越性,能夠克服傳統PPC的脆弱性缺陷。 圖13 s1(t)對的跟蹤效果 圖14 跟蹤誤差 圖15 控制輸入與輔助系統的狀態 針對現有PPC理論的脆弱性缺陷,系統闡述了非脆弱PPC新理論的基本構想。通過對傳統PPC理論框架與關鍵技術的回顧,簡要分析了導致其脆弱性問題的關鍵因素與作用機理。在此基礎上,探討了開辟非脆弱PPC新理論應當解決的關鍵基礎問題。最后,給出了非脆弱PPC新方法的技術實現方案。數值仿真結果證明了所提方案的有效性和相對于傳統PPC的優越性。下一步,將針對PPC脆弱性的度量問題,開展相關算法優化研究。5 數值仿真
5.1 受擾動力學系統的非脆弱PPC仿真

5.2 輸入受限動力學系統的非脆弱PPC仿真
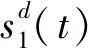

6 結語

