結合分裂Bregman的壓縮感知電磁地圖重構算法
林棟明, 王紅軍
(國防科技大學電子對抗學院,合肥,230037)
近年來,電磁地圖作為一種較為新穎的電磁頻譜管理和決策手段而倍受關注,其涵蓋了多種電磁信號輻射源,如雷達、無線電等,可有效反映區域電磁信號的時域、頻域和空域特征[1-2],支撐軍民領域對電磁態勢掌控的需求。
目前,該領域的研究主要是針對電磁地圖中的無線電環境地圖[3],而要實現區域無線電環境地圖的構建,首先要獲得區域內各個地理位置對應的無線電信息,尤其是每個位置的接收信號強度。隨著無人化、小型化技術的發展,利用分布式感知網絡實現電磁數據的獲取成為目前的首選方式[4]。但是分布式感知網絡并不能完全覆蓋目標區域,這就導致獲得的數據只能是部分的或殘缺的。所以,有必要研究如何利用殘缺的電磁感知數據重構出目標區域整體電磁態勢的技術。
經典的克里金插值法(Kriging)[5]、反距離加權插值法(inverse distance weighting,IDW)[6]等諸多插值方法均被引入用于電磁地圖的重構。文獻[6]改進了優化型Shepard算法(modified Shepard’s method,MSM)。該算法將一個相對值設定成權值,并且在處理數據時利用采樣點擬合一個特定形式的節點方程,并結合近鄰搜索,然后將節點方程的值應用于插值點的估計,從而提高了采樣點局部特征的利用率。雖然仿真結果顯示該改進算法的平均絕對誤差比經典的反距離加權插值法和優化型Shepard算法要低,但是,實驗樣本太少,存在局部最優的問題,適用場景小于反距離加權插值法。文獻[7]著眼于傳感器在無線電環境地圖構建上的戰術運用,通過不同的插值方法分析了傳感器數目對地圖構造質量的影響。實驗結果中,克里金插值法的結果較為平滑,其作用效果優于反距離加權插值法和最近鄰法(nearest neighbor,NN),實驗結果證明傳感器數量是除傳感器部署方式、密度、間距、插值方法以及傳播環境外,可對地圖質量造成影響的因素,以及克里金插值法在構建地圖上的優勢。總的來說,在電磁地圖的構建上克里金插值法效果較好,但是其所得結果難以準確體現輻射源所處區域附近的電磁信號分布情況;反距離加權插值法雖然使用場景廣泛,但是精度方面有待提高,且需要使用較多的感知節點。此外,插值法中的多項式回歸法[8]以及局部多項式法等也可實現電磁地圖的重構,其中多項式回歸法可更好地擬合非線性數據,但無法避免數據過擬合,而局部多項式法可有效捕捉短程變化,但在鄰域距離變化時作用效果難以保證。在分類上,插值法屬于直接法。地圖的構建方法還包括間接法以及混合法。間接法即通過構建電磁傳播模型實現地圖重構的方法,文獻[9]是利用位置估計實現衰落信道無線電環境地圖重構的一個例子,其主旨是利用估計的發射源位置實現每個位置的動態干擾預測。但是該方法的精度依賴于各個損失模型的經驗取值,如果信道發生突變,則所得結論準確性并不高,并且該方法需要掌握目標區域內的電磁傳播信息,而在非協作情況下,區域電磁環境信息顯然難以知曉。混合法則是直接法和間接法的結合,此類方法精度高,但是復雜度高且適用場景受限[10-11]。
在傳統信號恢復領域,奈奎斯特采樣定理一直被視為經典,直到壓縮感知(compressed sensing,CS)的出現[12]。壓縮感知使得僅用少量采樣數據即可實現原始信號的重建,因此,也有望實現電磁地圖的重構。目前,針對壓縮感知的研究多數集中于重構算法,這些算法主要分為兩類:解決最小l1范數的貪婪型算法[13]以及解決最小l0范數的凸優化類算法[14]。在多數學者的研究下,壓縮感知成功地解決了許多問題。如文獻[15]將其應用于地震數據的譜反演中。實驗證明所提方法復雜度低,且對于高頻信號具有較強的重構能力,但是作用效果受原始信號信噪比影響較大,低信噪比下的作用效果不佳。以及文獻[16]利用壓縮感知減少硬件中的計算量等。無獨有偶,Bregman迭代也是解決最小l1范數的有效方法[17]。另外,文獻[18]從壓縮感知入手,在數據重構時使用Bregman迭代進行數據恢復,并且用分裂Bregman實現噪聲去除,形成了雙重Bregman迭代的數據重構方法。該方法有效減少了算法的迭代次數并且可保證數據的重構精度,有效實現了地震數據的恢復。
由于電磁地圖涵蓋的范圍十分廣闊,本文只研究其中的電磁信號覆蓋強度地圖的重構(其后內容均稱為電磁地圖),利用等磁線繪制電磁地圖。等磁線類似于地質學上的等高線,可反映區域內電磁數據的變化情況。考慮到參考信號接收功率(reference signal receiving power,RSRP)在分析電磁信號的覆蓋情況時所得的結果比接收信號強度(received signal strength indicator,RSSI)更準確,因此算法研究中采用該參數作為衡量電磁信號強度的標準。
針對現有算法存在的不足,考慮到壓縮感知僅通過少量采樣信息即可將原始信號恢復出來[19]以及Bregman迭代在精度提升方面的較好效果[20],論文提出一種新型的結合分裂Bregman的壓縮感知電磁地圖重構算法,算法研究價值和創新點如下:
1) 提出了濾波式分區正交匹配追蹤算法(filtered subdistrict orthogonal matching pursuit,FSOMP)。通過將目標區域劃分為若干個小區域,并重構出各小區域的電磁地圖,再進行數據融合并利用中值濾波提升數據的精度,有效減少了重構時間;
2)利用分裂Bregman全變分迭代對壓縮感知得到的電磁數據進行處理,通過利用電磁數據之間的相關性提升數據精度,結果精度優于多種當前新近的算法。
由此,在非協作和采集數據殘缺條件下,實現對目標區域電磁態勢的重構。
1 模型構建
結合分裂Bregman的壓縮感知電磁地圖重構算法實現流程如圖1所示。
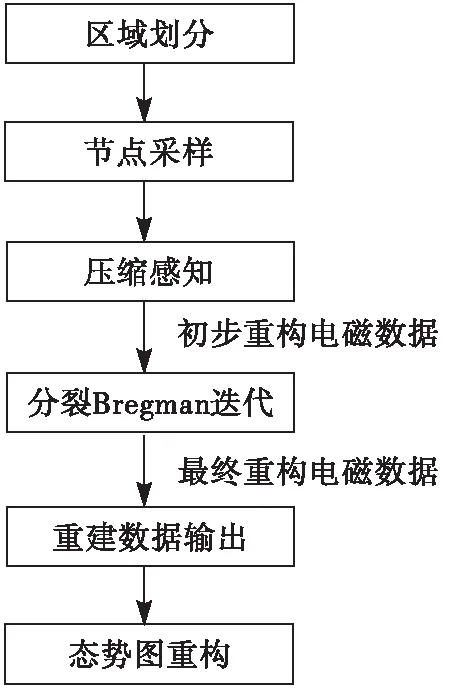
圖1 算法實現流程
算法首先依據電磁數據量將目標區域劃分成數個小區域,劃分之后每個區域的電磁數據量不超過8 000。電磁數據量的計算依據是電磁分辨率。所謂電磁分辨率是指將目標區域按照一定的長度進行柵格劃分(保證該長度同目標區域邊長的比值不大于0.01),并將每個柵格中心處所采集的電磁數據作為所在柵格電磁數據的代表,此時對應的柵格長度即為電磁分辨率。顯然,分辨率太大,所得的數據量就會過多,會導致運算量過大;分辨率太小,則所得到的數據就不能很好地表示區域內的電磁分布情況。如1 000 m×1 000 m的區域,電磁分辨率設為20 m,則該區域的電磁數據總量即為2 500。
然后利用感知節點對電磁數據進行采樣,再通過改進正交匹配追蹤算法對殘缺的采樣數據進行重構;之后根據該重構出的數據之間的相關性,利用分裂Bregman對數據進行精度提升。依據所得到的精度更高的數據,最終利用等磁線重構出目標區域趨于實際的電磁地圖。
1.1 基于壓縮感知的OMP算法改進
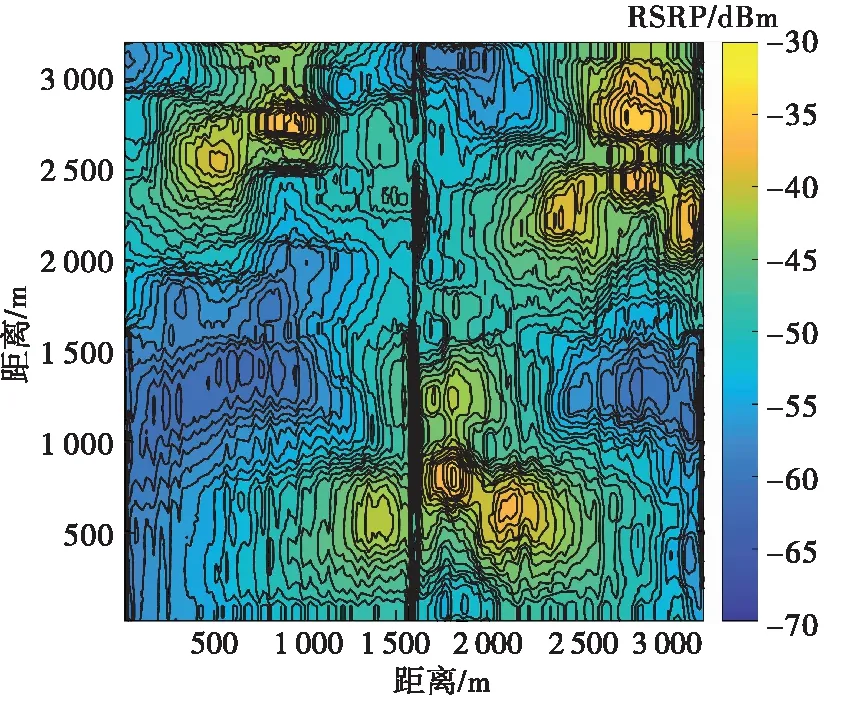
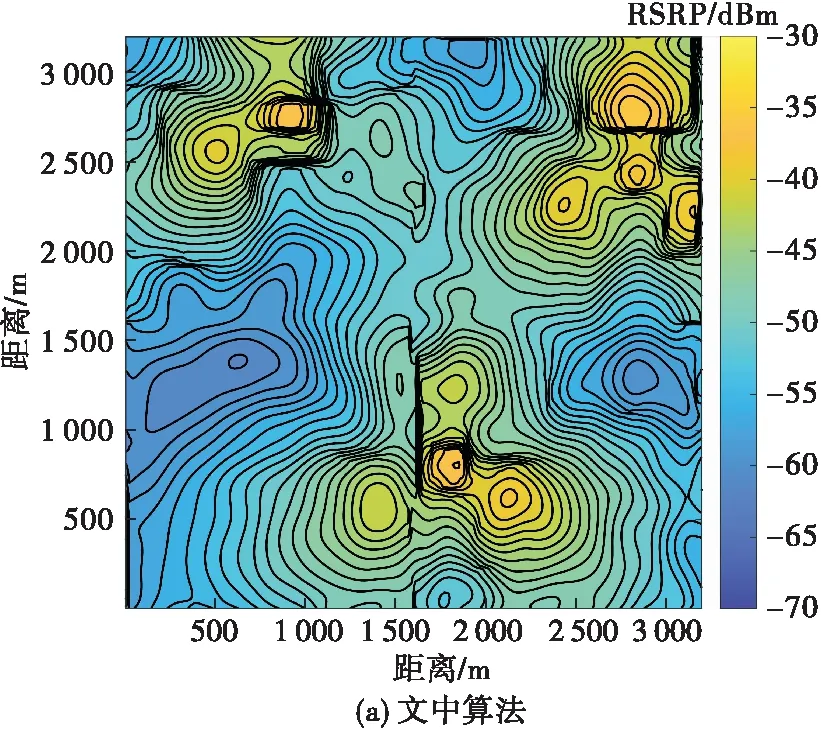
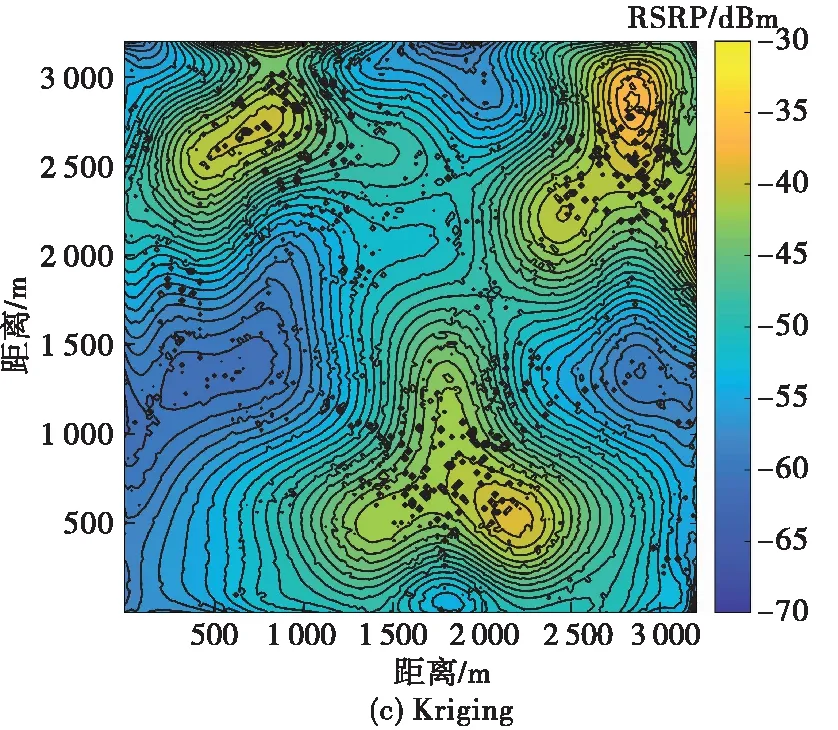
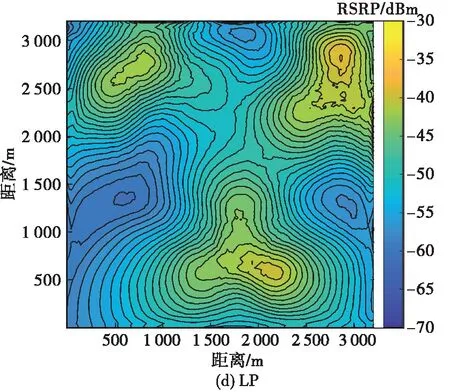
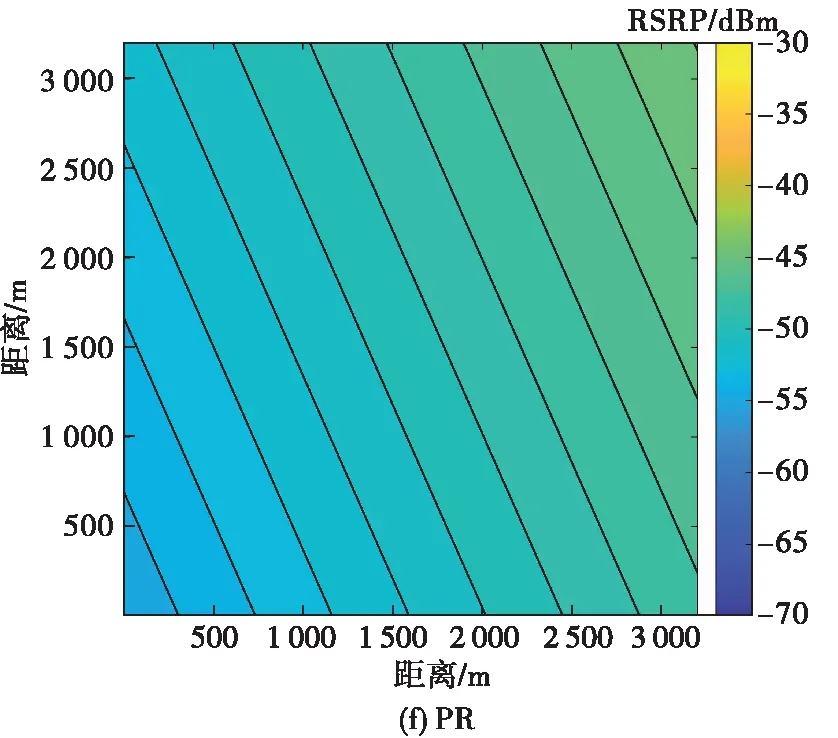
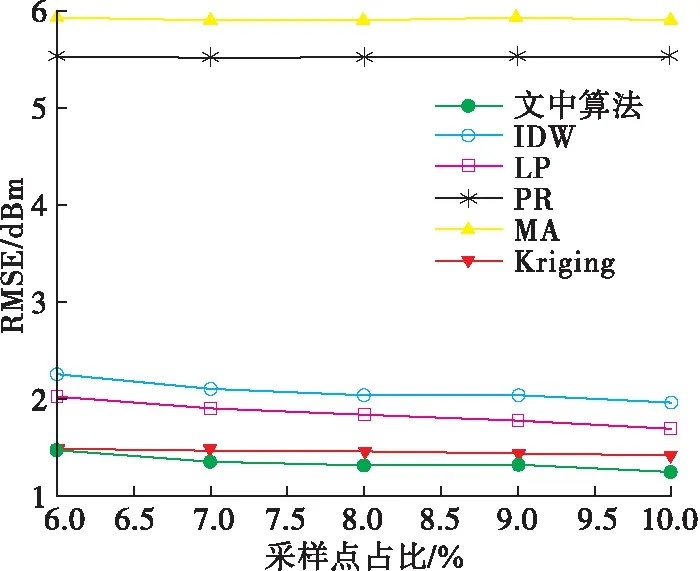
設存在一維信號x∈RN,其信號分量用xi表示,i∈[1,N]。此時,將該信號映射至一個M×N型的測量矩陣Φ上,可以得到測量值為y=[y1,y2,…,yM]T,這里要求M< y=Φx (1) 而在信號重構時,則是通過觀測值和測量矩陣反推出信號值。引入稀疏性約束以及信號稀疏化,重構過程就可以用式(2)描述如下: min ‖θ‖l0s.t.y=Aθ (2) 式中:A=ΦΨ稱作傳感矩陣;維度為N×1的θ中僅有少量非零元素;Ψ為N×N型稀疏基矩陣;‖?‖l0為l0范數。 在電磁地圖重構中,可將測量矩陣Φ調整為一個對角矩陣K,即將數據限定于一個規則的網格之中,根據已知的網格數據求取未知的網格數據,K滿足: (3) 式中:I為單位矩陣,表示已知電磁數據所在位置;0為零矩陣,表示未知電磁數據所在位置。 那么式(1)的求解即可轉化為對式(4)的求解: y=Kx (4) 式中:y為含有M個非零數值的N維列向量。 這里,針對正交匹配追蹤算法(orthogonal matching pursuit,OMP)進行改進并結合中值濾波提出了濾波式分區正交匹配追蹤算法,即FSOMP算法。該算法將目標區域分成數個小面積區域,分別在每個子區域中隨機拋灑一定數目的感知節點對其進行采樣,之后串行或并行重構出各個小面積區域的電磁數據,然后將數據進行融合得到目標區域的整體電磁數據,最后利用一維中值濾波器對其進行濾波處理。 FSOMP可有效避免數據量過多造成OMP算法運行出現奇異值導致精度下降的問題,同時大大減少了算法的運行時間。 算法的流程如下: 輸入參數:子區域傳感矩陣A,采樣數據y,迭代次數ε,原始算法為稀疏度,這里設為子區域電磁數據維度的均方根,轉換成列向量形式的K。 FSOMP得到的結果不夠精確,需要利用分裂Bregman進行精度提升,該處理可從不夠精確的重構數據中有效提取電磁數據間的相關關系,從而提高數據的精度。 分裂Bregman在求解正則問題上具有較好的效果,當用于求解全變量問題時,以各向異性為例[21-22],要求解如下問題: (5) (6) 利用Bregman迭代可得下式, (7) 為了解決以上問題,引入常規分裂Bregman,此時需解決下列問題: (8) 為了提高解決效率,為其引入高斯-賽德爾迭代(Gauss-Seidel),即: (9) 因此,基于分裂Bregman的各向異性全變量去噪的算法可以概述如下: 第2階段,迭代求值。當預測值和上一預測值之間差的l2范數小于閾值時,算法進行如下迭代: (10) 式中:shrink(τ,?)=(τ/|τ|)max (|τ|-?,0)。 第3階段,全變量迭代完成,輸出最終的重構電磁數據,然后利用該數據通過等磁線繪制出相應的電磁地圖。 電磁地圖重構算法的評價指標較多,其中關鍵性指標有以下4種。 1) 均方根誤差(root mean square error,RMSE) RMSE可有效衡量每個重構值和原始值的平均偏離程度,且能夠定量地表示所得重建數據的精度。計算式為: (11) 2) 決定系數R2 決定系數R2可有效反映數據預測重建結果和真實值之間的接近程度,該系數越大,則預測結果的分布越接近真實數據的分布,即所得地圖的無線電覆蓋情況和真實情況的一致程度越高,其計算過程見式(12): (12) 3) 電磁地圖重構質量 重構的電磁地圖必須以較高的質量表征出目標區域內的相關無線電信息,否則便無法為人類的實踐活動提供支撐,可以從有無牛眼現象、等磁線形態、異常值分布等方面進行判斷,所謂等磁線即類似于地理學上的等高線,表示區域電磁信號強度的變化情況。 4) 魯棒性 在可用節點數少于預期計劃時,算法的作用效果不能有太大變化,因此算法應具有較好的魯棒性,可以通過減少采樣點占比,觀察算法的均方根誤差大小以及變化情況來進行判斷。 因此,在驗證所提算法的作用效果時,論文從電磁地圖重構質量、均方根誤差、決定系數以及魯棒性對算法的作用效果進行評價。 提取Brussels地圖中3 200 m×3 200 m的區域,研究其中的LTE移動通信網的電磁覆蓋情況,并利用等磁線繪制電磁地圖,其實際電磁地圖如圖2所示。該區域中存在3個基站(以下均稱為輻射源),其最大發射功率為43 dBm,頻帶寬度設置為2110FDD-10 MHz,小區半徑為350 m。將該目標區域進行柵格化分,并設置電磁分辨率為20 m,最終可得到25 600個柵格,總計25 600個電磁數據。將該區域均分成4塊子區域,并在每個子區域隨機拋灑640個低成本的感知節點,即保證每個子區域都有一定數目的感知節點,共計隨機拋灑感知節點2 560個,采樣點(感知節點)占電磁數據總量的比例僅為10%,并認為這些節點均可獲得數據。性能評估基于core i9平臺采用蒙特卡洛仿真方法實現。 圖2 原始電磁地圖 算法在運行時將該目標區域分解成為了4塊子區域,邊長均為1 600 m,先利用FSOMP對該區域進行初步重構,其重構結果如圖3所示。 圖3 FSOMP算法運行結果 圖3是FSOMP得到的初步重構結果,盡管等磁線較為雜亂,但是均方根誤差僅為1.360 9。FSOMP實質為對電磁地圖的粗重構,即得到一個初步的結果。在得到粗重構結果后,需要利用分裂Bregman對粗重構的結果進行精重構,即進行精度提升,其結果如圖4(a)所示,此時的均方根誤差僅為1.254 5,且等磁線的形態同實際情況更加吻合。 正如前文所述,反距離加權插值法的應用場景廣泛,受限程度低;克里金插值法克里金插值法(Kriging)已被證明是重構電磁地圖的優秀算法;局部多項式法可有效捕捉數據的短程變化以及多項式回歸法(local polynomial, LP)可有效擬合非線性數據,因此將其設置為對照對象。此外,由于移動平均法(moving average,MA)可以消除突變值對整體數據的影響,可以減小電磁數據各種衰落現象的影響,因此也將其作為對照對象。分別將這5種插值方法用于電磁地圖重構,得到結果分別見圖4(b)~(f)。 圖4 不同算法下的電磁地圖重構結果 很明顯,經過第2階段的分裂Bregman迭代降噪,最終得到的結果質量有很大改觀,等磁線分布有序程度高,和原始的等磁線分布較為接近,可較好地反映輻射源所在區域的細節情況,且無牛眼現象,重構的地圖質量高;而反距離加權插值法所得結果等磁線分布最為雜亂且牛眼現象嚴重,因而所重構的電磁地圖質量低;而克里金插值法所得到的結果中,雖然等磁線的分布和原始的等磁線分布較為接近,但是存在一定程度的牛眼現象,導致等磁線略雜亂,所重構的電磁地圖質量并不高;而局部多項式法所得結果雖然沒有牛眼現象且等磁線分布和原始分布接近,但是在輻射源所在區域無法較好反映輻射源的細節情況,因此重構的地圖質量并不高。至于另兩種算法,從實驗結果看,二者均沒有什么異常值,但是根本無法準確的顯示該區域的電磁覆蓋情況,因此,從重構的地圖上判斷,這兩種算法并不適合用于電磁地圖的重構。 然后再分析算法所得數據的精度以及重構數據分布同實際電磁分布的一致程度。表1為本文算法、反距離加權插值法、克里金插值法等方法在感知節點占比為10%情況下的均方根誤差以及相應的決定系數。 表1 數據精度衡量1 從表1可明顯地看出,本文算法所得結果具有最小的均方根誤差,即精度最高;同時,由于決定系數最大,因此所得結果的電磁分布同實際電磁分布也最為接近。 分析算法的魯棒性。通過利用盡可能少的感知節點實現電磁地圖重構來評估算法優劣,即利用較低的占比并保證一定的作用效果。因此將采樣節點占比從10%減小至6%,即研究占比為10%、9%、8%、7%、6%對應情況下論文算法的作用效果,結果如圖5內各圖例表示的離散點所示。 圖5 算法魯棒性分析 從圖5中可以明顯看出,盡管采樣節點占比降低,但論文算法所得結果的均方根誤差一直是最小的,并且幅度變化并不劇烈,相差5%的數據量,均方根誤差僅僅提高0.229 0,而數值精度位于第二的克里金插值法雖然僅提高了0.072 9,但是其均方根誤差卻始終高于本算法;其他算法如反距離加權插值法提升了0.306 0、局部多項式法提升了0.336 8,多項式回歸法提升了0.004 6,移動平均法提升了0.008 3,但這些算法的均方根誤差均在2以上,重構精度不高,另外,移動平均法以及多項式回歸法的均方根誤差均在5以上,因此結合前述內容判斷此兩種算法不適宜用于電磁地圖的重構問題。 由于實際情況中,很多時候感知節點的數量不一定能夠滿足需求,因此,必須考慮極少感知節點可用情況下的算法重構效果。在這種情況下,對數據的精度要求比較高,下面主要從均方根誤差、決定系數兩個方面對算法性能進行分析。表2為考慮感知節點數量占電磁數據總量的比例為2%的情況下,算法的重構效果。 表2 數據精度衡量2 從表2可看出,本文所提算法所得結果有最小的均方根誤差值,且所得數據分布和實際電磁數據的分布最為接近,其次是反距離加權插值法、局部多項式法、多項式回歸法以及移動平均法;而克里金插值法在此種應用情況下所得結果誤差很大,并且所得數據和實際電磁數據偏差極大。 綜上所述,從電磁地圖重構質量、所得結果的均方根誤差以及決定系數和魯棒性這幾個方面來看,文中所提出的算法具有較好的性能。 針對分布式感知網絡在實際條件下難以實現對目標區域電磁態勢全覆蓋感知的問題,提出了一種結合分裂Bregman的壓縮感知電磁地圖重構算法。在壓縮感知部分,通過對OMP算法的改進,有效減少了算法運行時間并提高了所得重構電磁數據的精度;在分裂Bregman部分,通過引入分裂Bregman全變量去噪,進一步提取電磁數據之間的相關性,進而提高數據精度,最后重構出電磁地圖。仿真實驗證明,重構出的電磁地圖同實際的電磁覆蓋情況相接近且精度較高,算法具有一定的實際應用前景。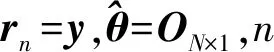

1.2 基于分裂Bregman的全變量迭代
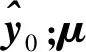
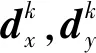
2 實驗仿真與性能分析
2.1 評價指標選取

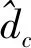
2.2 結果分析





3 結語

