基于和聲-遺傳算法的機(jī)械臂激勵軌跡優(yōu)化

劉金銘，劉梅，鐘佩思，梁中源，張超，王曉

(山東科技大學(xué)機(jī)械電子工程學(xué)院，山東青島 266590)

0 前言

為避免激發(fā)機(jī)械臂的高頻特性、減少噪聲干擾對參數(shù)辨識的不良影響，提高動力學(xué)參數(shù)的辨識精度，應(yīng)選取合適的算法優(yōu)化激勵軌跡。優(yōu)化后的激勵軌跡必須滿足關(guān)節(jié)角度、速度和加速度限制等約束條件，保持機(jī)械手運行的平穩(wěn)性，這是一個單目標(biāo)多約束問題。

GEE在2001年首次提出和聲搜索算法，之后該算法被廣泛應(yīng)用于分布式發(fā)電系統(tǒng)的許多領(lǐng)域，如參數(shù)優(yōu)化、全局?jǐn)?shù)值優(yōu)化和最優(yōu)無線脈沖響應(yīng)系統(tǒng)辨識等。NADI等提出了使用和聲搜索的自適應(yīng)參數(shù)控制方案，實現(xiàn)了勘探狀態(tài)和開發(fā)狀態(tài)之間的平衡過渡。HE等提出了和聲-遺傳算法，其中和聲算法用來生成遺傳算法的初始種群，使遺傳算法在搜索能力上得到了提升。

HOLLAND于1975年首次提出遺傳算法，遺傳算法的性能優(yōu)于其他元啟發(fā)式算法，例如模擬退火和粒子群優(yōu)化等，尤其是在大規(guī)模問題中。劉磊等人引進(jìn)S形函數(shù)優(yōu)化收斂因子，提出了改進(jìn)的基于S形函數(shù)的灰狼算法，避免了算法的“早熟”。蘇二虎結(jié)合懲罰函數(shù)和遺傳算法的優(yōu)點，雖然提高了算法的迭代速度，但導(dǎo)致算法容易“早熟”。楊從銳等通過種群平均適應(yīng)與最大適應(yīng)度的大小關(guān)系來判斷種群的離散程度，進(jìn)而調(diào)整種群的交叉和變異概率，加快了算法的收斂速度。閆春等人在前人基礎(chǔ)上引入反正弦函數(shù)，計算種群平均適應(yīng)度與最大適應(yīng)度的比值，更好更快地反映了種群離散度的變化，并且引入了交叉和變異順序的自適應(yīng)機(jī)制，增強(qiáng)了算法的搜索能力和搜索速度，但未考慮個體適應(yīng)度不佳時，交叉和變異概率的調(diào)整問題。

在上述研究的基礎(chǔ)上，本文作者改進(jìn)遺傳算法的順序自適應(yīng)和概率自適應(yīng)機(jī)制，結(jié)合和聲算法的優(yōu)點，提出改進(jìn)的和聲-遺傳算法。為驗證該算法的性能，使用和聲-遺傳算法得到SCARA型機(jī)械臂優(yōu)化后的激勵軌跡。

1 動力學(xué)建模及其線性化

1.1 SCARA型機(jī)械臂動力學(xué)建模

SCARA型機(jī)械臂的空間定位精度由連桿1、2、3共同決定，將連桿4視為連桿3的負(fù)載，如圖1所示。因此，僅對前3個工作臂進(jìn)行動力學(xué)建模。

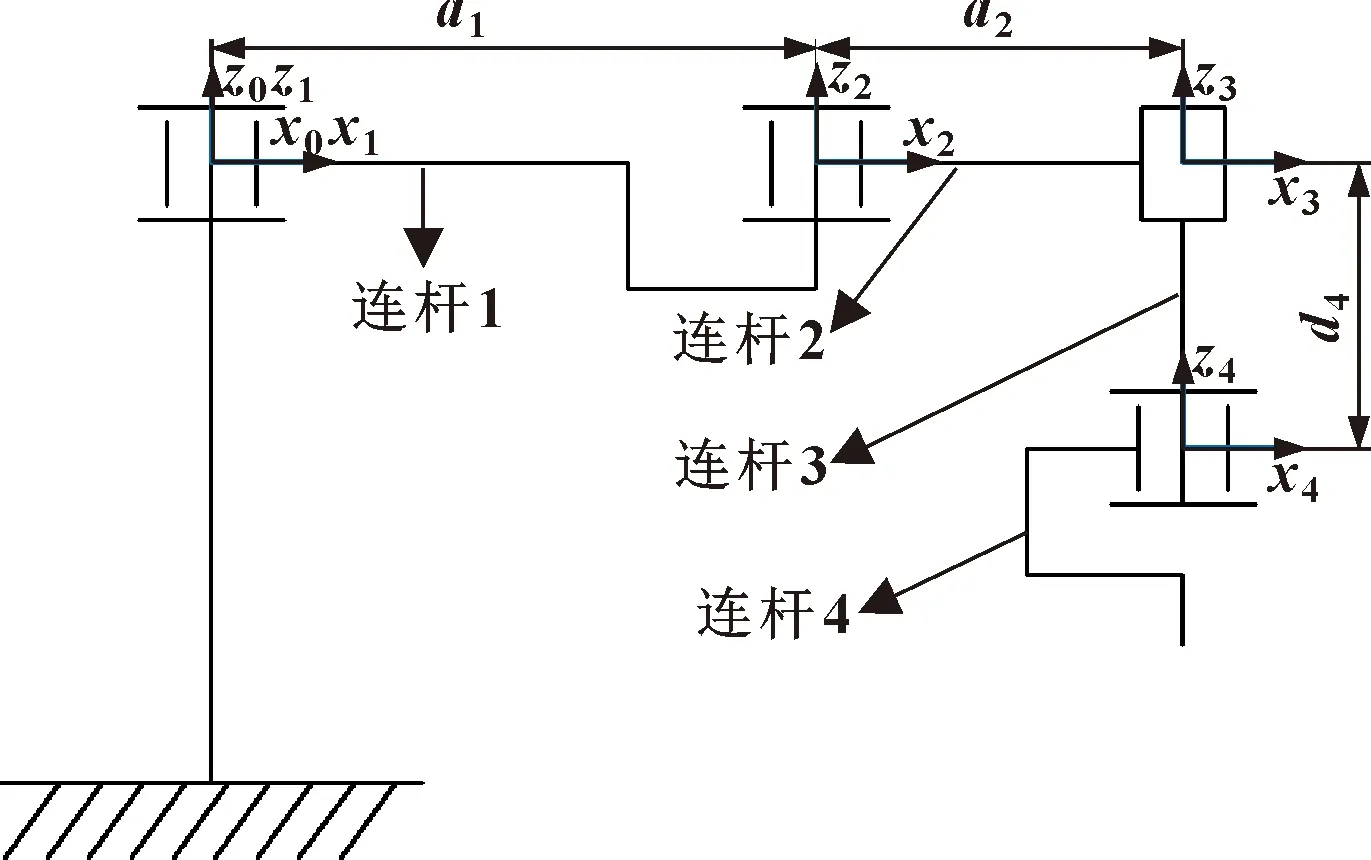
圖1 SCARA機(jī)器人D-H坐標(biāo)系

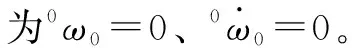
因為關(guān)節(jié)1、2為旋轉(zhuǎn)關(guān)節(jié)，關(guān)節(jié)3為移動關(guān)節(jié)，得到各關(guān)節(jié)的驅(qū)動力矩/力為

(1)

式中：

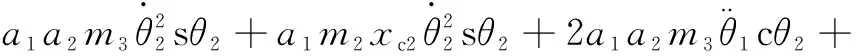
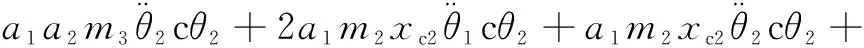
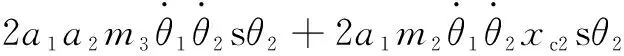
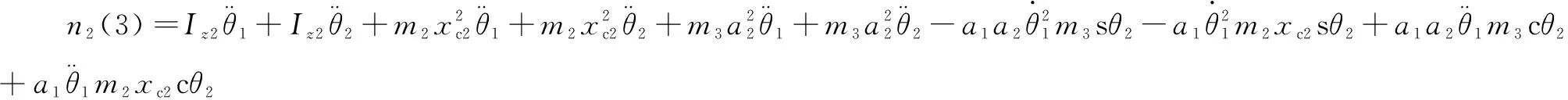
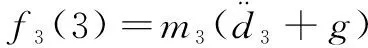
式中：c表示cos;s表示sin。

1.2 模型的線性化

將機(jī)械臂的動力學(xué)模型表示為其慣性參數(shù)與關(guān)節(jié)力矩的線形表達(dá)式：

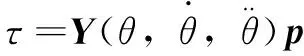
(2)

式中:為×10的觀測矩陣,為連桿數(shù)量；為待辨識慣性參數(shù)集,表達(dá)式為

=

[]

采用數(shù)學(xué)推導(dǎo)的方法，依次確定連桿3至連桿1的最小慣性參數(shù)和觀測矩陣為

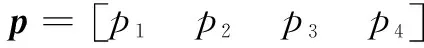
(3)

式中:

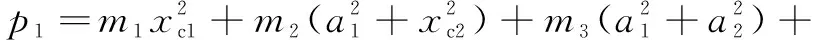
2+1

=+

=

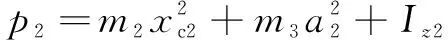
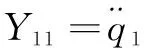
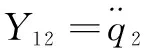
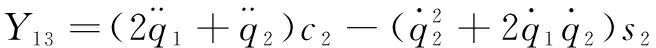
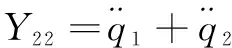
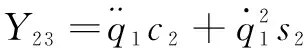
2 激勵軌跡及其優(yōu)化目標(biāo)

為減少噪聲干擾對參數(shù)精度的影響，應(yīng)在進(jìn)行激勵軌跡優(yōu)化之前選擇合適的激勵軌跡模型，避免激發(fā)機(jī)器人的高頻特性。

2.1 激勵軌跡及其約束

傅里葉級數(shù)公式為

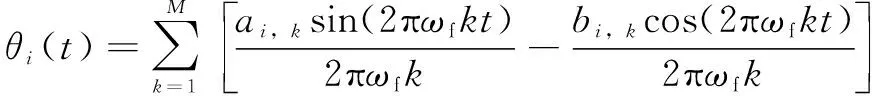
(4)

式中:為連桿編號；為正弦和余弦項的數(shù)目，=5；,和,為傅里葉級數(shù)的系數(shù);=2π,為基角頻率。

激勵軌跡需要滿足連續(xù)性、周期性和運行的平穩(wěn)性，即在軌跡起始和停止的位置，關(guān)節(jié)的速度和加速度為0。滿足上述要求的條件為

(5)

式中：和分別為軌跡起始和終止的時間。

2.2 優(yōu)化目標(biāo)

在進(jìn)行動力學(xué)參數(shù)辨識的過程中，階動力學(xué)參數(shù)辨識方程=由組觀測數(shù)據(jù)組成的回歸矩陣和關(guān)節(jié)驅(qū)動力矩矩陣組成。當(dāng)和存在擾動δ和δ時，待辨識參數(shù)集的相對誤差為

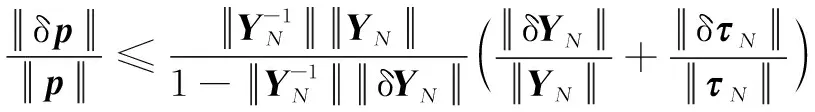
(6)

根據(jù)定義可知，回歸矩陣的條件數(shù)為

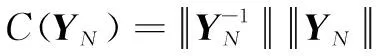
(7)

將公式(7)代入公式(6)可將待辨識參數(shù)集的相對誤差進(jìn)一步表示為

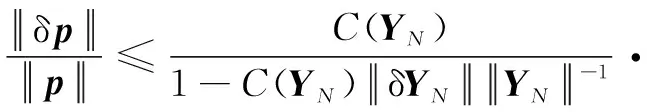
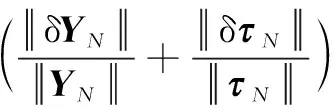
(8)

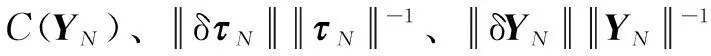
3 和聲-遺傳算法

軌跡優(yōu)化問題的關(guān)鍵是如何在滿足約束的條件下，快速、準(zhǔn)確地得到回歸矩陣的最小條件數(shù)。傳統(tǒng)的遺傳算法在一定程度上實現(xiàn)了這一功能，然而在搜索效率和穩(wěn)定性方面仍存在一些缺陷。

3.1 算法參數(shù)的初始化

算法的參數(shù)有和聲記憶庫的大小、音調(diào)調(diào)整率、隨機(jī)選擇率、和聲搜索算法迭代次數(shù)、交叉概率、變異概率和遺傳算法的迭代次數(shù)。基于經(jīng)驗，將和聲記憶的大小設(shè)置為50。音調(diào)調(diào)整率和隨機(jī)選擇率將直接影響算法的運行效果，根據(jù)經(jīng)驗將音調(diào)調(diào)整率和隨機(jī)選擇率的數(shù)值均設(shè)定為0.3。

3.2 種群的初始化

采用和聲算法選擇初始種群個體，在確定了和聲記憶庫的大小之后，隨機(jī)生成初始和聲，并儲存在和聲記憶庫HM中。以設(shè)定的隨機(jī)選擇概率生成新解，并以1-的概率在原搜索庫中選擇新解。根據(jù)音調(diào)調(diào)整率確定是否對新解進(jìn)行局部擾動，新的解是否優(yōu)于和聲記憶庫中的最差解。如果新的解比和聲記憶庫中的最差解更好，就將最差解替換為新解；反之，重復(fù)上述操作。

和聲記憶庫的初始化過程為

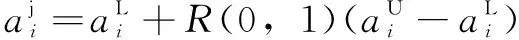
(9)

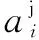
根據(jù)概率產(chǎn)生一個新的解決方案，公式如下：

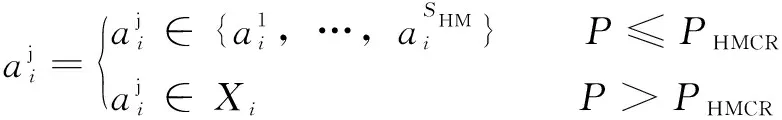
(10)

式中:為隨機(jī)選擇概率；為和聲庫之外的變量可行域。

需要進(jìn)一步檢查每個選定的矢量，以確定它需要在哪里進(jìn)行音調(diào)調(diào)整。

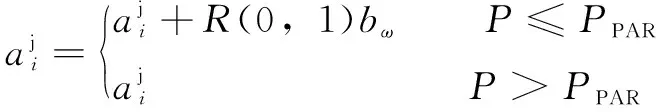
(11)

式中:為任意帶寬；為音調(diào)調(diào)整概率。

3.3 編碼方式

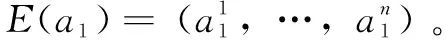
3.4 適應(yīng)度函數(shù)與選擇

因為()≥1，所以直接選擇()作為適應(yīng)度函數(shù)。為避免算法陷入局部最優(yōu)，將排序法和輪盤賭法相結(jié)合，提出輪排選擇法。每次計算適應(yīng)度值后首先進(jìn)行排序，從排名靠前的10個個體中隨機(jī)選擇2個個體保留下來；對剩余的個體進(jìn)行輪盤賭選擇，從而保證基因的多樣性。

3.5 改進(jìn)順序自適應(yīng)機(jī)制

傳統(tǒng)的遺傳算法，遵循選擇、交叉和變異的順序，但在種群相對集中的情況下，交叉的意義不大，種群依然有可能陷入局部最優(yōu)解。因此，本文作者提出順序自適應(yīng)機(jī)制，通過判斷種群的集散程度，確定交叉和變異的順序。當(dāng)種群較為集中時，先變異；當(dāng)種群較為發(fā)散時，先交叉。

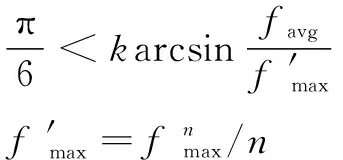
(12)

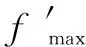
反正弦函數(shù)可以增大算法對種群離散度變化的敏感程度，通過調(diào)節(jié)離散度擴(kuò)大系數(shù)可以進(jìn)一步調(diào)整算法對種群離散度變化的敏感程度。如圖2所示，可知取值越大，算法對種群離散度變化越敏感。

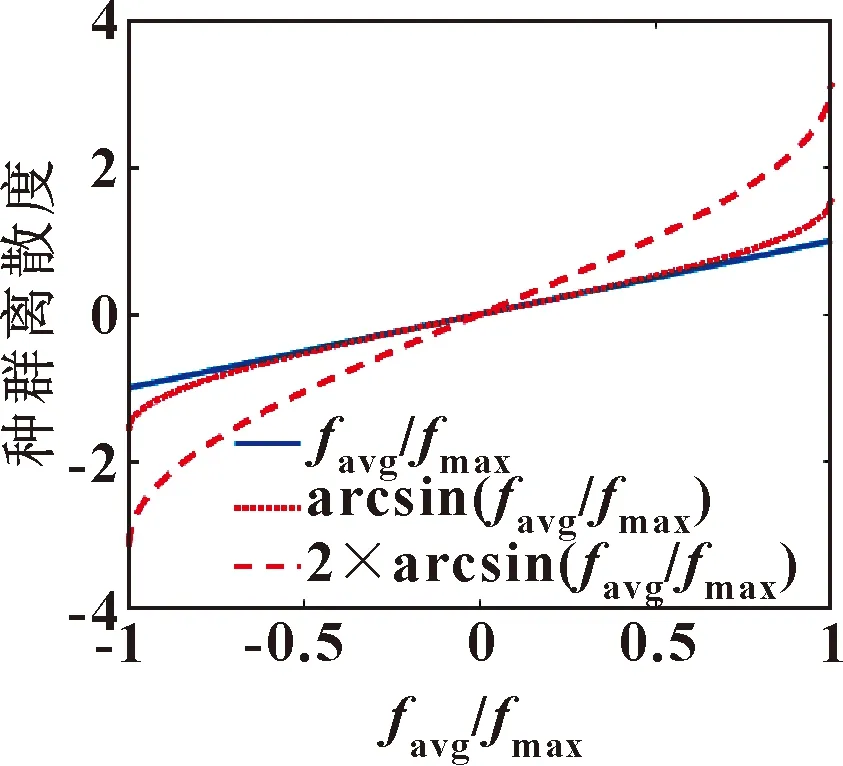
圖2 種群離散敏感度曲線

3.6 交叉概率和變異概率的自適應(yīng)機(jī)制

Sigmoid函數(shù)是最常用的神經(jīng)元激活函數(shù)，它在線性和非線性之間表現(xiàn)出良好的平衡性，如圖3所示。可知：當(dāng)≤-6時，()接近于0；當(dāng)≥6時，()接近于1。

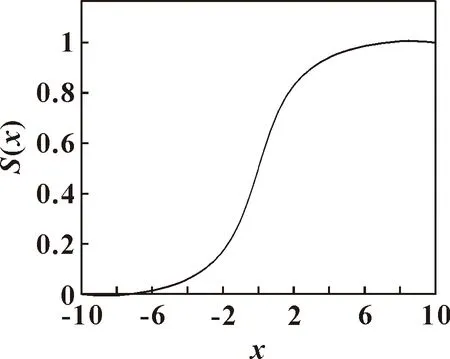
圖3 Sigmoid函數(shù)

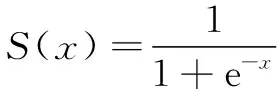
(13)

本文作者提出了一種基于S形函數(shù)的概率自適應(yīng)調(diào)整機(jī)制，如公式(14)(15)所示,使得交叉和變異概率可以根據(jù)每一個個體的適應(yīng)度自適應(yīng)地進(jìn)行調(diào)整。如果某個個體的適應(yīng)度大于或等于種群的平均適應(yīng)度，在交叉或變異概率的最小值的基礎(chǔ)上對其進(jìn)行自適應(yīng)調(diào)整；反之，則采用最大的交叉或變異概率。改進(jìn)自適應(yīng)遺傳算法流程如圖4所示。

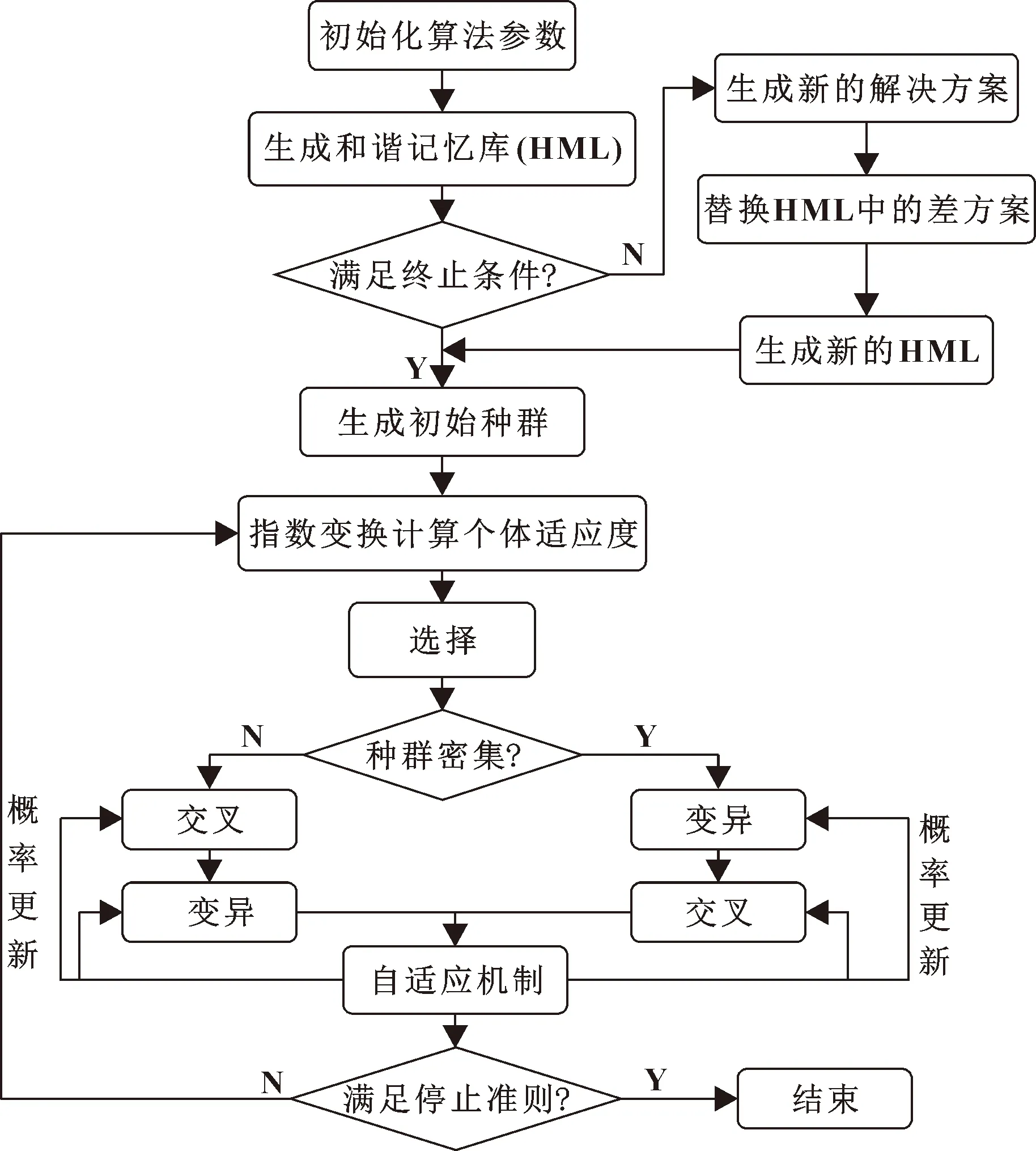
圖4 改進(jìn)自適應(yīng)遺傳算法流程

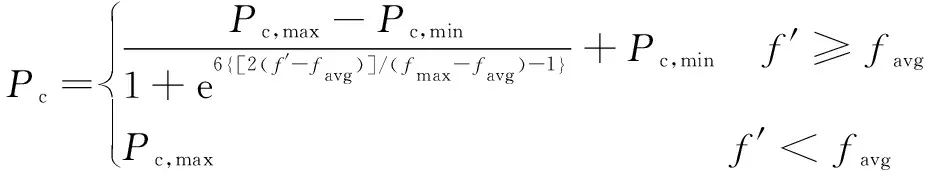
(14)

(15)

式中:、分別為交叉概率的上限和下限；、分別為變異概率的上限和下限；′為當(dāng)前種群中個體的適應(yīng)度。

4 激勵軌跡優(yōu)化實驗

SCARA機(jī)器人各關(guān)節(jié)角度、角速度和角加速度的限制范圍如表1、表2所示。

表1 關(guān)節(jié)1、2運動限制范圍

表2 關(guān)節(jié)3運動限制范圍

在簡化后的SCARA機(jī)器人中，連桿1、2的轉(zhuǎn)動和連桿3的移動是解耦的。因此，分別求取關(guān)節(jié)1、2和關(guān)節(jié)3的激勵軌跡。

根據(jù)公式(3)可知，前3個關(guān)節(jié)的回歸矩陣。關(guān)節(jié)1、2的激勵軌跡為傅里葉級數(shù)，5階共有22個待優(yōu)化參數(shù)。設(shè)置基頻=0.2π，迭代次數(shù)為400代，種群大小為60，交叉概率上下限、分別為0.9和0.1，變異概率上下限、同上。分別使用所提出的和聲-遺傳算法與文獻(xiàn)[14]和文獻(xiàn)[15]中提出的自適應(yīng)遺傳算法求解，結(jié)果如表3所示，進(jìn)而可得到前2個關(guān)節(jié)和關(guān)節(jié)3的觀測矩陣條件數(shù)分別為1.003 9和1.000 0。

表3 最優(yōu)化傅里葉級數(shù)系數(shù)

3種算法的迭代結(jié)果對比如圖5所示。可知:文中提出的和聲-遺傳算法收斂速度明顯優(yōu)于文獻(xiàn)[14]、文獻(xiàn)[15]中的自適應(yīng)遺傳算法。

圖5 回歸矩陣迭代情況

關(guān)節(jié)1、關(guān)節(jié)2和關(guān)節(jié)3的角度、角速度和角加速度變化分別如圖6和圖7所示。可知：優(yōu)化后的軌跡滿足公式(5)中的約束，可以保證機(jī)器人運行的平穩(wěn)性。

圖6 關(guān)節(jié)1、2的激勵曲線

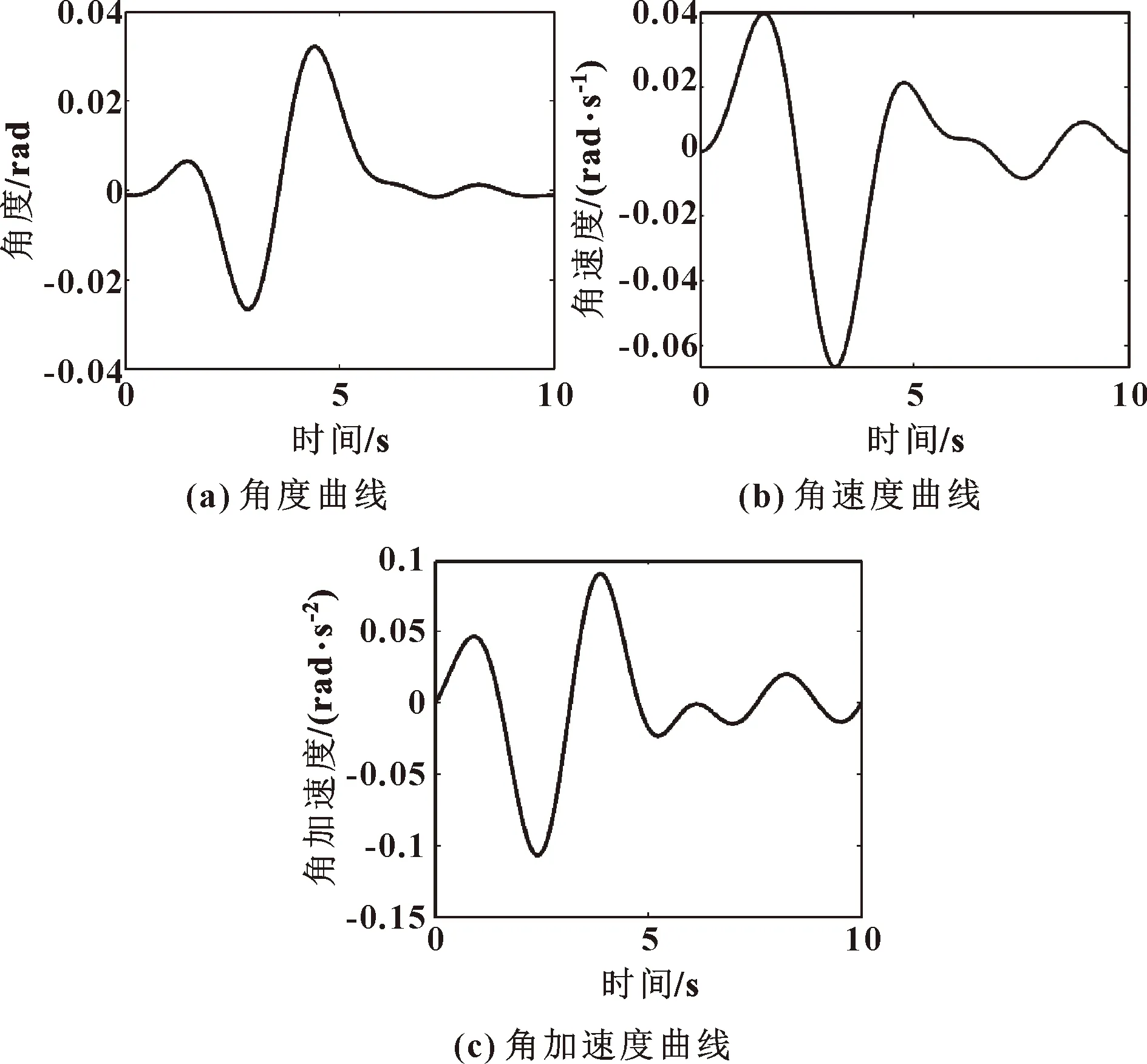
圖7 關(guān)節(jié)3激勵軌跡

關(guān)節(jié)3激勵軌跡對應(yīng)的觀測矩陣條件數(shù)為1，為最優(yōu)軌跡。這是因為關(guān)節(jié)1、2和關(guān)節(jié)3是解耦的，優(yōu)化關(guān)節(jié)3的激勵軌跡等同于求解單關(guān)節(jié)的激勵軌跡。

5 結(jié)論

(1)利用牛頓-歐拉法得到SCARA型機(jī)械手的動力學(xué)模型，并使用數(shù)學(xué)推導(dǎo)的方法對模型進(jìn)行線性化和參數(shù)分離，得到了SCARA型機(jī)械手前3個關(guān)節(jié)的觀測矩陣和待辨識的最小參數(shù)集。選擇5階傅里葉級數(shù)作為激勵軌跡，確定了優(yōu)化約束和目標(biāo)。

(2)使用和聲搜索算法生成遺傳算法的初始種群，使用反正弦函數(shù)判斷種群分布的程度，改進(jìn)了順序自適應(yīng)機(jī)制，提高了算法的收斂速度。根據(jù)種群平均適應(yīng)度、最大個體適應(yīng)度和個體適應(yīng)度′，非線性調(diào)整交叉概率和變異概率；改進(jìn)了概率自適應(yīng)機(jī)制，考慮了個體適應(yīng)度在每一代中的影響。

結(jié)果表明：與文獻(xiàn)[14]、文獻(xiàn)[15]中的自適應(yīng)遺傳算法相比，和聲-遺傳算法具有顯著的優(yōu)越性。