小樣本不平衡設備數據下的機器學習策略研究

陳 揚，劉勤明，梁耀旭

（上海理工大學 管理學院，上海 200093）

隨著我國科技水平的飛速發展，我國對設備的健康壽命預測準確度要求越來越高，很多關鍵設備一旦在服役期間出現事故很有可能會造成大量人員傷亡或巨大經濟損失[1]。因此，及時準確地檢查出設備的健康狀況問題至關重要。

隨著機器學習和深度學習的飛速發展，越來越多的人工智能技術開始普及。其中，機器學習中的代表算法支持向量機(support vector machine,SVM)、神經網絡(neural networks,NNs)、隨機森林(random forests,RF)和K 鄰近值算法被越來越多地運用到實際工業生產中。在機器學習與深度學習算法的實際應用方面，劉文溢等[2]提出了一種基于隱馬爾可夫鏈的設備壽命預測模型，并通過算例驗證了該算法在實際工業壽命預測領域的可行性。曹正志等[3]提出卷積神經網絡與雙向長短期記憶網絡相結合預測設備健康數據特征發展趨勢，并通過實驗證明了該方法的有效性。但是，現階段越來越多的算法只面向大規模數據，在小樣本不平衡數據下很多算法不再適用，因此，發展面向小樣本不平衡數據的算法存在必要性[4]。

SMOTE (synthetic minority oversampling technique)算法是目前適用較多的合成少數類過采樣技術，它是基于隨機過采樣算法的一種改進方案。由于隨機過采樣采取簡單復制樣本的策略來增加少數類樣本，這樣容易產生模型過擬合的問題，即使得模型學習到的信息過于特別而不夠泛化。SMOTE 算法的基本思想是對少數類樣本進行分析，并根據少數類樣本人工合成新樣本添加到數據集中。SMOTE 算法本身也存在很多問題，首先鄰近值的選擇難以確定，同時面對異常值以及不平衡數據分布的時候表現并不理想。針對以上問題，Han 等[5]提出了一種Borderline-SMOTE 算法，目前這也是最廣為人接受的改進算法。楊賽華等[6]在此基礎上提出了一種BN-SMOTE 改進算法，利用最近鄰思想構建處于決策邊界附近的多數類樣本集，再一次確定邊界區域難以學習的少數類樣本點從而構建一個新的少數類樣本集。楊毅等[7]在Han 的研究基礎上提出了一種RB-SMOTE 的改進模型，通過合成不平衡率不一的多個新訓練樣本，組成相應的多個基分類器，再采用投票的方式對測試樣本進行分類。Bansal 等[8]提出了SMOTE-M算法規避數據不平衡帶來的問題。王超學等[9]提出了一種GA-SMOTE 算法提高SMOTE 面對不平衡數據集的分類性能。以上幾種算法均對SMOTE 算法進行不同程度的改進，但是，面對多數類樣本中存在的噪聲的問題并沒有進行有效處理，因此，以上幾種改進算法并不能很好地對已有數據進行優化。

在此基礎上，面對存在問題的數據，傳統KNN 算法也無法處理不平衡數據和噪聲問題，因此，不能直接應用于大多數情況下的設備壽命數據處理。同時，當不同種類樣本點分布較為緊密時，KNN 算法難以對數據進行有效分類。針對此情況，本文提出了一種ISMOTE 算法(Improvement-SMOTE)，通過改進SMOTE 算法克服了傳統SMOTE 算法存在的問題，使得改進后的新增數據不再出現邊緣化、存在異常值、分類結果不夠泛化等弊端。由于傳統KNN 算法無法面向小樣本不平衡以及存在異常值的數據，利用ISMOTE 算法改進后的數據剛好可以彌補KNN 算法的不足，使得KNN 算法可以應用在存在小樣本不平衡數據的設備壽命預測領域。其次，在實際工業生產中，出現問題的數據有時會和正常設備的數據緊密分布，當不同種類的數據分布較為緊密時，KNN 算法的分類效果并不好。針對此問題，本文提出了一種投票式KNN (Voting-KNN,VKNN)算法。根據測試集數據分布以及數據種類引入PSO(particle swarm optimization)尋求每個設備狀態數據分布的中心點，隨后通過計算同簇樣本點到中心點的歐式距離均值建立分隔閾值，對到中心點距離小于的數據點利用“投票法”判斷數據種類，拋棄傳統KNN 算法計算k個距離最近樣本點從而判斷樣本種類的法則，規避數據混淆引起的誤差。優化后的數據通過改進KNN 算法在準確分析設備健康狀態的同時也可以有效預測設備未來健康發展趨勢。

1 問題描述

目前機器學習領域越來越多的算法只適用于面向大量有效數據的情況。而面向小樣本不平衡數據，誤用傳統機器學習算法很有可能會導致人們對設備的壽命產生錯誤預測從而造成巨大的經濟損失[10]，因此，在數據不足的情況下可以通過數據增強提高樣本質量[11]。面對傳統KNN 算法無法處理不平衡和異常數據的情況，本文采用改進SMOTE 算法（ISMOTE）。ISMOTE 算法首先對數據進行新增處理，采用類似k鄰近值原理剔除分布較為分散的異常數據，在保持數據特征的前提下人工合成符合條件的數據，解決了傳統SMOTE算法新增樣本出現新增樣本點質量低、容易邊界模糊以及新增后數據分布出現異常的問題。最后，通過VKNN 算法對優化數據進行分類，模型如圖1 所示。

圖1 基于ISMOTE-VKNN 模型的設備數據分析流程Fig.1 Equipment data analysis process based on the ISMOTE-VKNN model

2 改進SMOTE 算法

2.1 面向不平衡分類問題的SMOTE 算法

SMOTE 即合成少數類過采樣技術[12]，它是基于隨機過采樣算法的一種改進方案。由于隨機過采樣采取簡單復制樣本的策略來增加少數類樣本，SMOTE 算法的基本思想是對少數類樣本進行分析并根據少數類樣本人工合成新樣本添加到數據集中，算法流程如下：

a.對于少數類中每一個樣本x，以歐氏距離為標準計算它到少數類樣本集中所有樣本的距離，得到其k個近鄰。

b.根據樣本不平衡比例設置一個采樣比例以確定采樣倍率N，對于每一個少數類樣本x，從其k個近鄰中隨機選擇若干個樣本，假設選擇的近鄰為xn。

c.對于每一個隨機選出的近鄰xn，分別與原樣本按照如下的公式構建新的樣本。

很顯然，由于設備會受到運行環境以及狀況等一系列條件的影響，從設備中提取的數據可能并不能直接用于SMOTE 算法進行優化。傳統SMOTE 算法存在很多局限性，根樣本或輔助樣本中存在噪聲可能會導致新增樣本出現質量問題。在特殊情況下新增樣本處于多數類與少數類樣本的邊界區域會導致數據集出現邊界模糊的情況，而在此情況下使用傳統SMOTE 算法同樣會加重原先就存在的問題。因此，本文提出了一種改進SMOTE（ISMOTE）算法，該改進算法可以對以上問題進行規避，從而可以在數據存在問題的情況下對設備健康狀況進行評估。

2.2 ISMOTE 算法

面對存在異常值點，也就是噪聲的問題。這里的噪聲是指出現在多數類樣本群中的孤立的少數類樣本，在設備數據方面表現為數據看起來正常但是實際上已經因為某些原因無法正常運行的那一類。針對這種情況，本文選擇設置噪聲比例β對每個少數點進行評估。噪聲比例β的表達式為

式中：NMin為k鄰近值中少數類樣本個數；NMaj為多數類樣本個數。

設置噪聲標準α，x為 樣本集。

若β＞α，按照如下公式構建新樣本：

否則刪除該樣本點。

該改進法則的核心思想為通過噪聲比例判斷某種類樣本集中是否出現一定數量的其他種類樣本，如果出現頻率低于所設置的閾值，則將那些出現的點視為噪聲并刪除。此過程是在保留樣本分布特征的情況下對數據集進行優化，并不會影響后續步驟。

而當設備數據中正常數據與異常數據過于接近的情況發生的時候，針對傳統SMOTE 算法中可能出現的邊界模糊的情況，本文通過計算每個少數類樣本點與周圍最近的多數類樣本點的歐式距離，通過與設置的閾值進行比較從而選擇性地對部分少數類樣本點進行新增樣本的處理，歐氏距離的表達式為

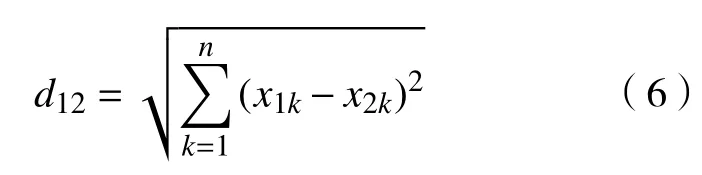
該改進算法不僅僅能處理二維數據，針對以多分類為目標的問題也可以優化多維數據集。

為了防止少數類樣本點和多數類樣本點在新增過程中分布過于接近，需要設置閾值dmin，這里設樣本點計算出的實際距離為d。

設d＜dmin的樣本點集為xi，則剩下的樣本點集為

同樣地，在特殊情況下多數類樣本和少數類樣本本身的分布可能就存在問題，即健康的設備數據和不健康的設備數據總是雜糅或是過于稀疏，這也會直接導致優化后的新增數據不夠泛化。部分區域過于密集或是過于稀疏都會導致新增樣本之后加重本身就存在的問題。一旦在這種情況下強行利用SMOTE 算法進行新增處理可能會導致最后利用機器學習算法分類時候準確性不足。因此，可以采用類似B-SMOTE 算法進行處理。

本文根據Han 提出的Borderline-SMOTE 算法的啟發采用如下算法進行處理，這里計算少數類樣本與周圍同類k鄰近值的距離d并通過設置閾值m進行比較。根據比較的結果數量將樣本點分為以下幾類：

設樣本點x∈xMin

a.若對于任意x，都有d＜m，則x=xn

b.若對于任意x，至多50%樣本的d＜m，則x=xh，從中隨機抽取部分樣本點xi進行新增處理，xi∈xh，抽取比例為25%～50%

c.若對于任意x，大于50%樣本的d＞m，則x=xu，采用傳統SMOTE 算法新增樣本。

隨后按照以下步驟對不同樣本種類的樣本點x進行處理:

忽略xn，

利用此方法可以解決數據本身存在的分布不均勻問題，同時將此方法與上述方法進行結合可以有效地對原本存在諸多問題的數據進行處理，將其變為可以被KNN 算法進行運算的數據。同時，優化后的數據可以規避傳統KNN 算法中可能帶來的種種問題。

ISMOTE 算法流程如圖2 所示。

圖2 ISMOTE 算法流程圖Fig.2 Flow chart of ISMOTE algorithm

該改進算法不僅最大程度保留了樣本集的分布特征，同時也在刪除噪聲、消除邊界模糊、優化少數類樣本分布方面對數據集進行了一定程度的優化，彌補了傳統SMOTE 與B-SMOTE 的不足，使得經過該算法優化處理后的數據能夠被目前大部分機器學習算法計算。

3 VKNN 算法

3.1 KNN 算法分析

KNN（K-Nearest Neighbor）法即k最鄰近法，最初由 Cover 和Hart 于1968 年提出，是一個理論上比較成熟的方法，也是最簡單的機器學習算法之一。該方法的思路非常簡單直觀：如果一個樣本在特征空間中的k個最相似（即特征空間中最鄰近）的樣本中的大多數屬于某一個類別，則該樣本也屬于這個類別。該方法在定類決策上只依據最鄰近的一個或者幾個樣本的類別來決定待分樣本所屬的類別。KNN 算法的核心思想是，如果一個樣本在特征空間中的k個最相鄰的樣本中的大多數屬于某一個類別，則該樣本也屬于這個類別，并具有這個類別上樣本的特性。該方法在確定分類決策上只依據最鄰近的一個或者幾個樣本的類別來決定待分樣本所屬的類別。KNN 方法在類別決策時，只與極少量的相鄰樣本有關。

在KNN 算法理論方面，Yadav 等[13]比較了KNN 算法與其他機器學習算法在處理分類問題時的準確度，并從數學角度證明了KNN 算法擁有不錯的分類能力。Xu 等[14]將KNN 與超球結構相結合，使得改進后的KNN-MVHM 算法能有效處理不均衡數據，規避了傳統KNN 算法的局限性。殷小舟[15]針對支持向量機超平面附近的測試樣本分類錯誤的問題，改進了將支持向量機分類和k近鄰分類相結合的方法，形成了一種新的分類器。在分類階段計算待識別樣本和最優分類超平面的距離時，如果距離差大于給定閾值，可直接應用支持向量機分類，否則用最佳距離k近鄰分類。李歡等[16]提出了一種有效的k近鄰分類文本分類算法，即SPSOKNN 算法，該算法利用粒子群優化方法的隨機搜索能力在訓練集中隨機搜索，在搜索k近鄰的過程中，粒子群跳躍式移動，掠過大量不可能成為k近鄰的文檔向量，并且去除了粒子群進化過程中粒子速度的影響，從而可以更快速地找到測試樣本的k個近鄰。以上算法都對KNN 算法進行了改進，提高了分類精度以及分類速率，但是卻沒有解決KNN 算法數據分布重疊導致分類誤差較大以及無法面向不平衡數據的問題，因此，上述算法在預測設備健康狀態時并不適用。

3.2 VKNN 算法

本文在面向給定數據時，首先利用前文ISMOTE算法對數據本身進行優化，將優化后的數據傳遞給KNN。優化后的數據剛好規避了傳統KNN 算法最大的幾個問題，能夠更加有效地對數據進行計算。

在傳統KNN 算法中，k的取值一直是一個比較困擾的問題。如果k值過低可能會出現過擬合的問題，不能很好地泛化。如果k值過高可能使得模型過于泛化，出現欠擬合的問題[17]。針對此問題，本文不再使用KNN 算法中根據k近鄰樣本點種類作為分類依據的原則。通過利用粒子群算法尋優速度快的特點首先對訓練集樣本點進行中心點搜索，隨后計算同簇樣本點到中心點距離均值作為分隔閾值對樣本點進行分隔，最后對分隔后的樣本點進行種類“投票”處理并輸出分類結果。在粒子群算法中，個體和群體間需要不斷交互信息從而尋找最優解。在此過程中，粒子通過式(10)和式(11)不斷更新自己的速度Vid和位置Xid。

式中：ω為慣性因子；C1與C2為加速常數，一般取2；Pid為第i個變量的個體極值的第d維度；Pgd表示全局最優解的第d維度。

當滿足最大迭代次數時迭代停止并輸出最優解。

a.樣本點集合為

b.建立適應度函數為

搜尋到的樣本點xn中心坐標為(xn,yn)。

c.根據歐氏距離式(6)對同簇樣本點到該種類樣本分布中心進行計算，計算出的距離合集D={d1,d2,···,dm}，根據式(12)計算同簇樣本到中心點距離均值

d.若di＜，則納入隔離樣本集Dnew。

e.判斷Dnew中多數類樣本種類并作為最終輸出結果。

相比傳統KNN，該算法克服了因為k取值不同而會出現不同分類結果的問題，針對相同數據集VKNN 算法每次分類結果都相同。同時，通過引入粒子群算法可以最大程度提升VKNN 算法的計算效率，避免在尋找同簇樣本距離均值過程中花費太多計算時間。在實際生產過程中，盡可能減少計算時間與盡可能提高算法計算效率無疑會給企業生產效率帶來巨大提升。

4 基于ISMOTE-VKNN 的算法流程

基于ISMOTE-VKNN 算法流程如下：

a.收集設備狀態的數據，將其數據進行預處理后按照2∶1 的比例分為訓練集與測試集。

b.根據企業要求確定噪聲標準α，計算每個少數類樣本的噪聲系數β并進行比較，從而選擇合適的樣本點。

c.設置距離閾值dmin并計算少數類樣本距離d進行比較，選擇合適的樣本點。

d.通過計算k鄰近值并判斷樣本狀態選擇不同的新增方式。

f.分隔樣本點并生成Dnew。

g.進行投票，輸出分類結果。

ISMOTE-VKNN 流程圖如圖3 所示。

圖3 ISMOTE-VKNN 算法分析流程圖Fig.3 Flow chart of ISMOTE-VKNN algorithm analysis

5 ISMOTE_VKNN 仿真分析

5.1 數據來源

使用美國卡特彼勒公司液壓泵與凌津灘水電站8 號機水導軸承狀態數據進行實驗，通過該數據以驗證SMOTE_KNN 算法的有效性。液壓泵與水導機器的故障一般是以軸承振動的方式表現出來，液壓泵實驗每隔10 min 進行一次約1 min 的設備振動數據收集，隨后對收集的數據進行特征提取以達到能夠被本文模型處理的要求。水導軸承實驗通過記錄不同負荷下的軸承橫向與縱向振動數據以分析軸承的壽命情況。本文將液壓泵前2/3 的數據用于訓練，用剩下1/3 的數據進行測試以驗證模型的有效性。同時針對水導軸承數據采用同樣的方式進行模型驗證，具體步驟和前者相同并省略。仿真環境為Anaconda 3.0。

5.2 數據分布

為了表現出ISMOTE_KNN 算法的優越性，本文將初始的多維數據進行拆分處理，即將原本的多維數據分為n個二維數據并挑選其中一組進行驗證。使用CH1-1 與CH1-9 振動數據進行模擬。圖4 為進行處理后的二維振動數據點位分布。

圖4 振動數據點位分布Fig.4 Distribution of vibration data points

從圖4 中可以看出，少數類樣本中存在孤立于多數類樣本中的異常值點。其中，黑色點為振動數據存在異常的點，橙色點為狀況健康的點，黑色類為少數類樣本，橙色類為多數類樣本。該數據無法直接用傳統KNN 算法進行處理，如果直接使用SMOTE 算法進行處理會出現上文描述的大量問題，因此，需要使用ISMOTE 對數據進行優化以達到KNN 算法使用的標準。

5.3 ISMOTE 算法

通過應用貝葉斯后驗概率[18]計算得出k取4，通過對少數類樣本計算噪聲比例并設置閾值可以將其中的異常值點找出。這里噪聲比例α取0.1。通過對所有少數類樣本點計算噪聲比例β，得到如表1 所示的結果。

表1 β 與閾值α 的比較結果Tab.1 Comparison results for β and threshold α

很明顯存在一個異常值點，該點β值為0，將其剔除。

即使將異常值點剔除，剩余的少數類樣本依然存在與多數類樣本十分接近的點。因此，將dmin設置為0.5，忽略容易導致邊界模糊的點。

利用ISMOTE_KNN 模型設置距離閾值m=0.5，k=4，同時通過計算可得模型中的少數類樣本點均為半正常樣本，隨機性地對符合新增要求的樣本點進行新增處理。將數據按照ISMOTE 算法進行處理可得到新增樣本數據如圖5 所示。

圖5 ISMOTE 算法處理后的數據分布Fig.5 Data distribution after ISMOTE algorithm processing

在新增樣本點過程中，為了保證ISMOTE 算法不會影響原始數據的特征，提取原始數據與新增數據的異常點擬合壽命曲線如圖6 所示。

圖6 原始異常數據點擬合曲線Fig.6 Fitting curve of original abnormal data points

如圖7 所示，在進行ISMOTE 新增處理后的數據幾乎不會影響原始數據點的壽命擬合曲線，因此，使用ISMOTE 算法優化數據是有效、可行的。

圖7 ISMOTE 異常數據點擬合曲線Fig.7 Fitting curve of ISMOTE abnormal data points

5.4 VKNN 算法

在ISMOTE 的基礎上引入VKNN 算法。其中，在PSO 算法中，經過實驗確定 ωini=0.9，ωend=0.4，C1=C2=1.5，最大迭代次數為100。

最終PSO 輸出的同簇樣本中心分別為(3.12，6.45)與(2.29，6.16)。根據式(12)計算出=0.373，=0.411。由此對樣本點進行分割處理，對處理后的數據種類進行分類并利用“投票”選擇最終結果。

用12 組測試數據利用VKNN 算法對設備健康狀況處理結果如表2 所示。

表2 ISMOTE_VKNN 設備數據預測結果Tab.2 Prediction results of equipment data based on ISMOTE_VKNN

如果不使用ISMOTE_VKNN 算法，直接進行KNN 算法計算結果如表3 所示。

表3 KNN 設備數據預測結果Tab.3 Equipment data prediction results based on VKNN

通過比對可以表明，相比傳統KNN 算法，ISMOTE_VKNN 算法擁有更高的準確性，并且2 種算法的耗時在面對小樣本數據的時候都很短，在時間上也繼承了KNN 算法的快速性。

同時為了保證ISMOTE_KNN 算法的優越性，而利用同樣的測試集與訓練集，在ISMOTE 優化數據的基礎上利用非線性SVM[19-20]以及僅僅對原始數據用非線性SVM 進行分類效果如表4 所示。

表4 SVM 與ISMOTE_SVM 處理結果Tab.4 SVM and ISMOTE_ SVM processing results

由于測試集樣本容量較小，所以，ISMOTE 算法的優越性主要體現在了容量相對較大的訓練集上。

將以上結果進行整合如表5 所示。

表5 液壓泵各算法正確率展示表Tab.5 The correct rate of each algorithm of hydraulic pump

可以看出，在液壓泵小樣本情況下雖然訓練集錯誤率已經明顯降低，但是，由于測試集的錯誤率偏高，幾乎接近直接使用KNN 算法進行計算的錯誤率，由此可以看出，ISMOTE_KNN 算法在小樣本數據處理中的優越性。

利用同樣的方式對水導軸承的振動數據進行分析和計算，得到的結果如表6 所示。

表6 水導軸承各算法正確率展示表Tab.6 Accuracy display table of hydraulic guide bearing

通過國內的水導軸承振動數據分析可知，ISMOTE_KNN 算法在實際應用中相比傳統機器學習算法以及其他聯合算法擁有更好的分類效果，即便是少數類樣本容量不足也能夠對其數據進行處理。相比大多數情況下使用的SVM，本文的算法能夠更加準確地對液壓泵狀態進行分析從而淘汰那些狀態異常的設備。

5.5 剩余壽命預測

在實際工業中，設備振動方均根值RMS能夠體現設備健康狀況，因此，本文通過對設備訓練集與測試集數據點的RMS數值進行觀察，觀察結果可作為分析設備健康狀況的依據。本文數據點的RMS數據計算結果如圖8 所示。

圖8 設備數據點RMS 監視數據Fig.8 RMS monitoring data of equipment data points

根據設備的健康狀況以及對數據點的分析，當RMS數據區趨于7 及以上的時候設備健康狀況將會導致設備無法完成預計的生產目標。因此，本文著重對7 及以上RMS的數據點進行分析和預估并擬合數據線性趨勢。其中，設備真實RMS數據值與預測RMS數據對比圖如圖9 所示。

圖9 RMS 實際值與測試值比較圖Fig.9 Comparisons of RMS actual value and test value

同樣地，對軸承的振動數據進行分析并擬合出機器剩余壽命RUL預測曲線如圖10 所示。

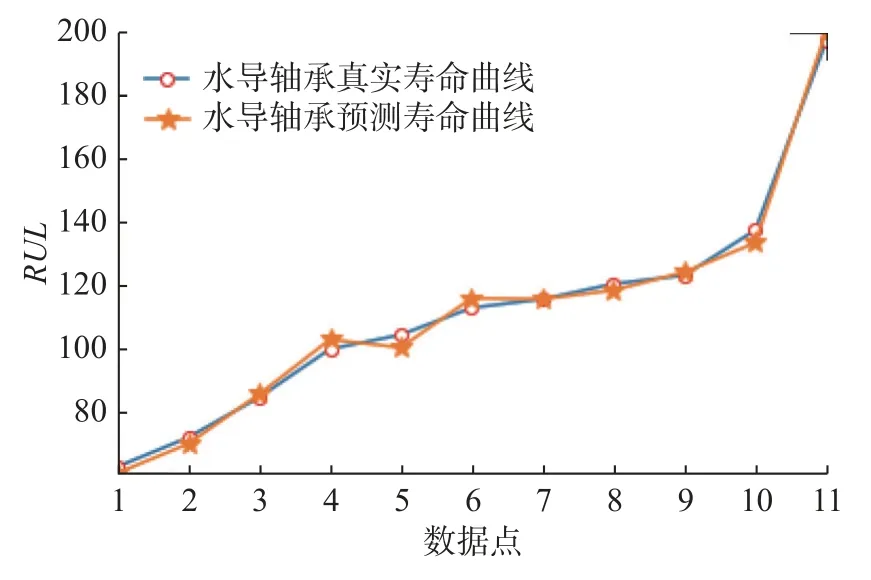
圖10 水導軸承RUL 實際值與測試值比較圖Fig.10 Comparison between actual RUL value and test value of hydraulic guide bearing

通過觀察2 個設備真實RMS數據線性擬合結果與本文算法的預測擬合結果可知，兩者具有高度的相似性，因而可以證明本文提出的算法在數據處理中不僅可以保證不會破壞數據的特征，同時也可以準確分析出設備健康狀況以及預測設備未來壽命發展趨勢，進而可以避免實際工業中因為設備健康問題而造成的經濟損失。

6 結束語

通過引入SMOTE 算法彌補KNN 算法存在的局限性，同時針對傳統SMOTE 算法的不足進行改進，通過設置噪聲比例β消除存在于多數類樣本附近的少數類樣本噪聲，再通過設置閾值dmin忽略那些新增后容易導致邊界模糊的少數類樣本點，選擇性地對部分優秀的樣本點進行新增處理，提高了新增樣本點的質量，規避了傳統SMOTE 算法存在的局限性。最后通過PSO 尋找同簇樣本中心，建立分隔閾值對樣本點進行裁剪并投票，規避KNN 算法面對交錯數據無法準確分類的問題。仿真部分比較了各種算法下液壓泵與水導軸承的健康狀況分析準確度。算例表明，本文提出的聯合算法相比傳統機器學習算法具有更高的準確性。在面對大規模數據時，當數據本身呈現出緊密離散型分布特點并且樣本分布毫無規律時，本文提出的改進算法由于法則限制會出現較大偏差，在此情況下可以適當拋棄ISMOTE 并需要對后續的機器學習改進算法進行進一步提升。在保持計算精度要求的前提下可以對VKNN 算法進行集成處理輸出強學習器Adaboost。為了保證該集成算法的計算速率，后續可以從樣本權值與弱學習器權值方面對Adaboost 進行進一步優化以滿足計算速率要求。同時為了適應實際工業中多維數據的情況，本文提出的算法在未來改進后應盡可能實現同時對多個因變量進行分析的功能，規避分類討論的局限性，由此滿足實際工業中的各種需求。