滑動鉆進造斜率預測與分析

王舸 黃文君 高德利

中國石油大學石油工程教育部重點實驗室

底部鉆具組合(BHA)是井眼軌跡控制的核心部件，其造斜率的準確預測和控制是復雜結構井工程的關鍵技術之一［1-10］。國內外學者對導向鉆具造斜率的預測方面做了大量的研究，其預測方法主要經歷了幾何法［11］、力學法［12-13］、軌跡法［14］、極限造斜率法［15］的過程。

幾何法假設BHA處于小變形狀態或鉆具組合長度較短的情況下，將鉆頭、下穩定器、上切點當作同一圓弧上的3個點，求解該圓弧的曲率作為BHA的造斜率，然而該方法并未考慮鉆具剛度及鉆井參數［16-17］。力學法采用靜力學計算導向鉆具組合鉆頭處的機械合力，將合力作用線與井眼軸線的夾角作為導向工具造斜率的預測結果，但該方法并未考慮鉆頭切削性能和地層各向異性［18-21］。軌跡法通過計算鉆頭側向力和鉆壓聯合作用下的合位移，確定合位移方向與鉆頭軸線的夾角，闡明了鉆進過程中的運動趨勢，但是鉆進趨勢角與造斜率之間缺少明確的定量關系，不利于造斜率的準確評估。極限曲率法采用了最小勢能原理，將鉆頭側向力為0或趨近于0時的井眼曲率作為導向工具造斜率的評價標準，但是未充分考慮鉆頭切削性能和地層各向異性的影響。總之，目前造斜率的計算方法仍存在不足，加之參數的不確定性，使得導向工具造斜率的理論計算值與實際值存在較大的誤差。

本文在前人研究的基礎上，綜合考慮工具結構、鉆井參數、軌跡參數及鉆頭-地層相互作用等影響，建立了基于零側向鉆速準則的滑動鉆進造斜率計算方法，并從“杠桿效應”和“鐘擺效應”的角度揭示了造斜率的影響機理，為導向鉆具組合的結構設計、造斜率預測、鉆具優選及鉆井參數優化等提供了分析手段。

1 滑動鉆進鉆具受力分析

1.1 導向鉆具力學模型分析

在定向鉆進過程中，導向工具受到鉆壓、扭矩、支反力、自重等載荷作用。將BHA分解成多個梁的組合，針對每一段梁，考慮縱向和橫向載荷的作用來計算梁的變形，建立BHA的三維力學模型。由于鉆頭處在井斜平面、方位平面內都會存在側向力的作用，在鉆壓、側向力的作用下，井下管柱所受多種載荷的大小、方向也會進行相應變化，鉆出的井眼軌跡為三維曲線，因此可將三維力學問題轉化為兩個二維力學問題進行求解，控制方程為

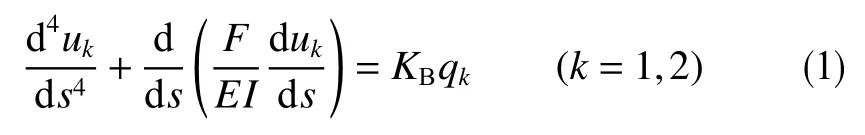
式中，k=1代表井斜平面，k=2代表方位平面；uk為管柱在井斜平面或方位平面上的橫向位移，m；s為管柱任意一點的弧長，m；EI為相應的抗彎剛度，N· m2；F為軸向力，N；KB為管柱的浮力系數，KB=1?ρd/ρs；ρd為鉆井液密度，g/cm3；ρs為管柱的材料密度，g/cm3；qk為管柱線重投影到井斜平面或方位平面的分量，N/m；由于井斜平面與方位平面相互垂直，管柱線重qk在方位平面上的投影始終為0，即q2為0。

本文利用加權余量法求解了導向鉆具組合的變形問題，需要構造BHA的變形試撓度函數作為控制方程的近似解，即可令BHA第j跨的試撓度函數為

式中，Ck,i, j為井斜平面和方位平面的待定系數，無因次；n表示導向鉆具單元節點個數，節點包括BHA的結構彎角、穩定器、管柱與井壁的接觸點等。

假定底部鉆具的下部邊界為鉸支約束，鉆具上端躺在井眼底邊，即

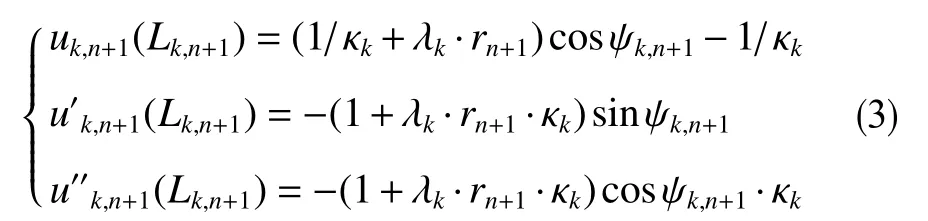
將式(2)代入到邊界條件式(3)中可得到關于Ck,i, j的線性方程，將式(2)代入到控制方程式(1)并利用子域法可得到關于Ck,i, j的線性方程。由于鉆具上切段長度是待定的，因此需要采用迭代法求解所有的未知量。

鉆頭處(j=1)的軸向力F1和支反力Nsk，1可表示為

其余各跨節點 (j=2,···,n+1)的軸向力Fj和支反力Nsk，j表示為

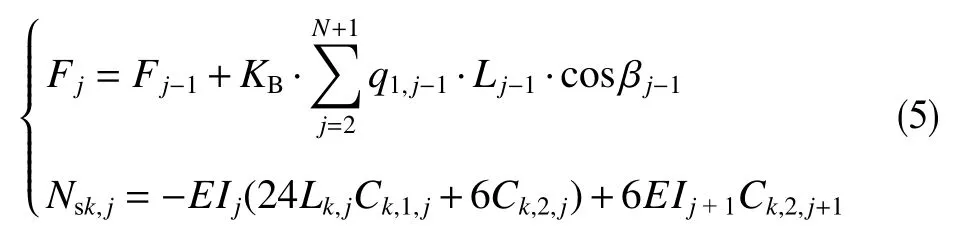
式中，Wob為鉆壓，一般無論對于井斜平面還是方位平面，鉆頭處的軸向力F1等于鉆壓，N；Nsk，1為鉆頭處的支反力，可表示為鉆頭處井斜平面和方位平面的側向力，N；L j?1為管柱第j?1 跨的弧長，m；Lk, j為管柱在井斜平面和方位平面第j跨的弧長，m；βj?1為管柱第j?1 跨的井斜角，rad。

1.2 滑動鉆進時鉆具軸向摩阻計算

在定向造斜過程中，一般采用滑動鉆進方式進行導向鉆進。然而在實際工況中，接觸點產生較高的摩阻會使得BHA難以連續滑動，甚至會大大降低管柱的軸向力傳遞效率，因此需要合理計算滑動鉆進時管柱的摩阻分布。依據式(4)、式(5)，可得到三維井眼中各跨段管柱的軸向載荷和摩阻計算公式。

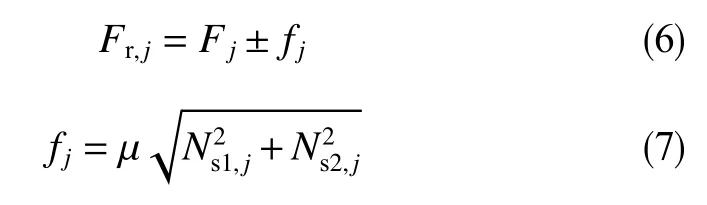
式中，Fr, j為第j跨管柱的實際軸向載荷，N；fj為第j跨管柱的摩阻，N；μ為管柱的軸向摩阻系數。

2 滑動鉆進造斜率計算方法

2.1 鉆進軌跡三維鉆速方程

在鉆頭與地層相互作用的影響下，鉆頭的位移方向并非與其機械合力方向一致。為了得到更加精確的造斜率計算模型，本文考慮BHA實際鉆進過程的影響，即側向鉆速為0，建立滑動鉆進造斜率的計算方法。

根據式(4)，進一步考慮鉆頭與地層相互作用［18］，建立井斜平面和方位平面上的鉆速方程。

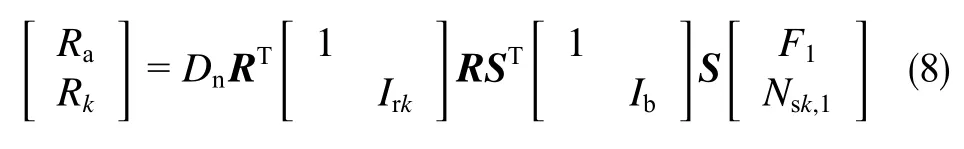
式中，Ra、Rk分別為沿井眼軸線方向、井斜以及方位

平面側向方向上的鉆速分量，m/h；Dn為標準(法向)鉆井效率；R為井底坐標與地層坐標的轉換矩陣；S為井底坐標與鉆頭坐標的轉換矩陣；Irk為地層各向異性指數；Ib為鉆頭的各向異性指數。

由于式(3)中的井眼曲率κk并未得到解決，因此第1次迭代所得到鉆頭在井斜平面和方位平面處的側向力Nsk，1中含有井眼曲率κk。為了確定式(3)中的井眼曲率κk，需要在第1次迭代的基礎上，基于零側向鉆速準則，對式(8)再次進行牛頓迭代求解，可構造目標函數為

考慮滑動鉆進過程中工具面的影響，結構彎角的存在會導致BHA的作用方向線與管柱軸線構成一個工具面。在滑動鉆進時，由于鉆頭側向力的變化，導致工具造斜能力無法用某一特定的工具面去進行表述，因此需要通過調整裝置角從0°到 360°的變化范圍來表征結構彎角的方位，如圖1所示。

圖1 滑動鉆進工具面的示意圖Fig.1 Schematic diagram of the tool face during sliding

圖1中x、y、z軸相互正交并構成了井斜α平面和方位φ平面，交點為鉆頭；N表示正北方向；Φc為裝置方位角，rad；Azc為導向鉆具投影在水平面上的方位角，rad；ω為高邊模式中，工具面與井底平面的交線所轉過的裝置角，rad；θ為導向鉆具的結構彎角值，rad。

根據圖1，結構彎角的方位表示為

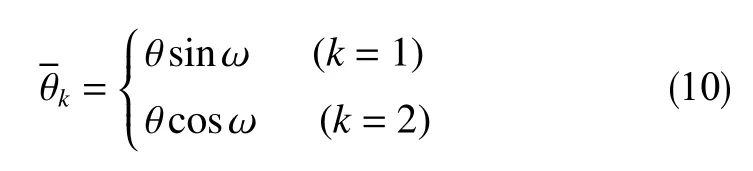
根據式(9)，利用牛頓迭代法進行求解，并引入式(10)中結構彎角方位變化的影響，將側向鉆速為0時井眼曲率作為滑動鉆進的造斜率，計算公式為

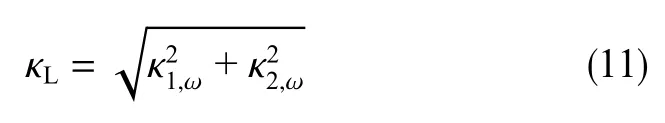
式中，κL為滑動鉆進在某一工具面下的理論造斜率，κ1,ω和κ2,ω分別為BHA在某一工具面對應的造斜率在井斜平面和方位平面上的投影，rad/30 m。

2.2 折算系數反演法

根據鉆速方程式(8)可知，鉆頭各向異性指數Ib和地層各向異性指數Irk的確定是準確預測工具造斜率的關鍵所在。一般地，Ib和Irk可以通過實鉆資料進行反演計算。當Ib=1時，鉆頭為各向同性；當0＜Ib＜1時，鉆頭的軸向切削能力強，并且當Ib越小時，鉆頭的軸向切削能力越強；當Ib＞1時，鉆頭的側向切削能力強。然而，即使在均質的各向同性地層條件下，鉆頭實際的運動軌跡也并非沿著機械合力的方向。對于Irk而言，在考慮地層層面各向差異和Ib的影響下，會使得Irk確定更加困難。因此，本文假設地層為各向同性的均質地層(Irk=1)，進一步簡化了式(8)計算的復雜性，并引入折算系數對式(11)進行修正，得到實際造斜率的計算公式為

式中， κA為滑動鉆進時真實造斜率，rad/30 m；λ為折算系數，無因次。引入折算系數，可將地層各向異性、實鉆過程等參數引入到造斜率預測模型中，λ的取值范圍大致為0.3~0.9。

3 實例分析

3.1 折算系數反演

以涪陵地區一口頁巖氣水平井為例，該井完鉆井深 4 734 m，水平段長度 1 930 m (包括口袋長度30 m)，造斜點深度 489 m，水平位移 2 421.45 m。該井的水平井段長，地層承壓能力低，密度窗口窄，鉆進時易發生竄氣、竄水等復雜情況，致使在滑動鉆進過程中，隨著井深的增加，摩阻越來越大，井眼軌跡難以得到良好的調控。現場施工在造斜段中使用的鉆具組合及對應的工況參數如下。

鉆具組合：?215.9 mm 混合鉆頭+?172 mm×1.25°單彎螺桿+浮閥+?127 mm無磁承壓鉆桿+LWD短節 (411×410)+?127 mm 無磁承壓鉆桿+?127 mm 加重鉆桿×9 根。參數：鉆壓 120~160 kN，方位角 180°，鉆井液密度1.39 g/cm3，鉆頭各向異性指數0.2。

依據該井的實鉆軌跡數據、鉆具組合參數、工況參數以及鉆頭的切削特性，反演計算了滑動鉆進工具的造斜率，繪制了造斜率折算系數反演圖版，并采取相對誤差來評估造斜率計算模型的精度，如圖2所示。工程中一般采用(°)/30 m作為造斜率的單位，因此本文將結果圖中造斜率數值的理論結果單位 rad/30 m 換算成 (°)/30 m。

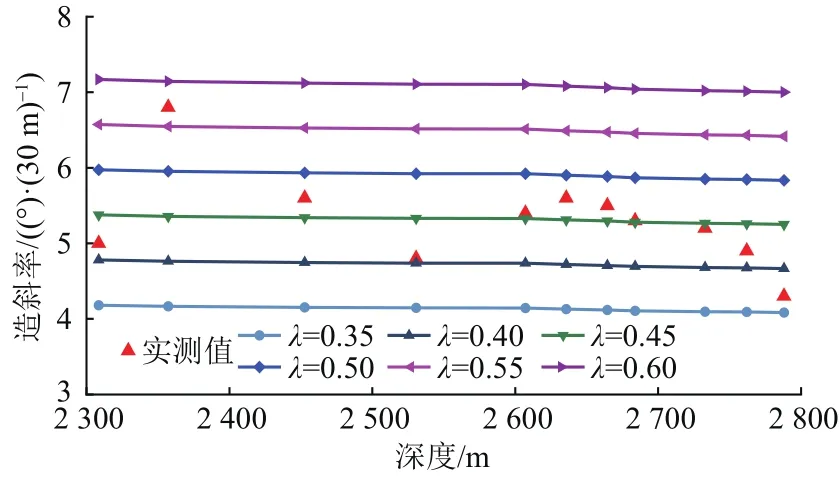
圖2 滑動鉆進造斜率折算系數反演圖版Fig.2 Inversion chart of the build-up rate conversion coefficient during sliding

圖2結果表明，滑動鉆進工具造斜率的實測值主要分布在折算系數(λ)取值為0.4~0.5之間，當折算系數取值為0.45時，造斜率實測值與預測值的平均相對誤差為6.36%，驗證了造斜率預測模型的合理性。該折算系數綜合考慮了地層各向異性、鉆進過程等影響，為涪陵地區鉆具優選、鉆井參數優化等提供依據。

3.2 滑動鉆進造斜率敏感性分析

針對于不同的工具結構，本文分析了滑動導向在不同鉆壓、井斜角、鉆頭各向異性及工具面下造斜率的影響規律，計算結果如圖3~圖6所示。整體結果表明，滑動導向模式下導向工具結構彎角(θ)對造斜率的敏感性大于鉆井參數、軌跡參數及鉆頭側向切削能力的敏感程度。由于結構彎角值的增加，加大了彎角與井壁之間的接觸，有利于杠桿效應的充分發揮，因此BHA的整體造斜能力也將不斷提高。

3.2.1 鉆壓的影響

圖3為滑動鉆進過程中，井斜角為60°條件下，造斜率隨鉆壓的變化。對于具有增斜效應的滑動導向工具而言，造斜能力隨鉆壓的增加而增強，然而當鉆壓增加至120 kN后，造斜率的整體趨勢略微下降，其主要原因是高鉆壓下結構彎角處的支反力與鉆壓之比變小，進而減弱了結構彎角對鉆進軌跡的作用。

圖3 滑動鉆進時造斜率隨鉆壓的變化Fig.3 Build-up rate vs.weight on bit during sliding

3.2.2 井斜角的影響

圖4為滑動鉆進過程中，鉆壓值為140 kN條件下，造斜率隨著井斜角的變化規律。結果表明，當井斜角由40°變化至60°時，造斜率呈現略微增大的趨勢。因為該過程結構彎角接觸井壁產生的杠桿效應大于BHA在重力作用下產生的鐘擺效應，并且產生的杠桿效應會增加鉆頭對地層的側向切削作用；隨著井斜角繼續增加，造斜率略微下降，因為隨著滑動鉆進接近于水平段，BHA在重力作用下產生的鐘擺效應逐漸增強。

圖4 滑動鉆進時造斜率隨井斜角的變化Fig.4 Build-up rate vs.well inclination during sliding

3.2.3 鉆頭各向異性指數的影響

圖5分析了鉆壓140 kN、井斜角60°條件下，鉆頭各向異性指數Ib對造斜率的影響規律。隨著Ib的增大，鉆頭的側向切削能力不斷增強，進而提高了工具的造斜能力。說明軌跡變化能力與鉆頭的側向切削能力密切相關，提高鉆頭的側向切削能力，有利于導向工具杠桿效應的充分發揮。

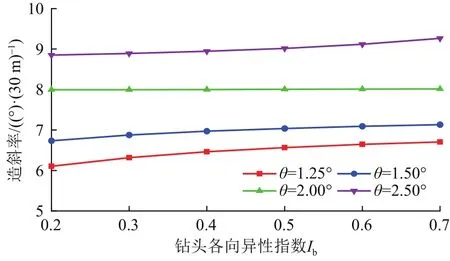
圖5 滑動鉆進時造斜率隨鉆頭各向異性指數的變化Fig.5 Built-up rate vs.bit anisotropy during sliding

3.2.4 工具面的影響

圖6分析了鉆壓140 kN、井斜角60°條件下，不同工具面對造斜率的影響規律。對于具有增斜效應導向工具而言，當工具面指向井眼高邊 (ω=0°) 時，結構彎角上部鉆柱重力會加強結構彎角處產生的杠桿效應，此時工具造斜率最大；隨著工具面順時針旋轉至井眼低邊(ω=180°) ，結構彎角上部鉆柱重力會抑制杠桿效應，使得造斜率逐漸降低。

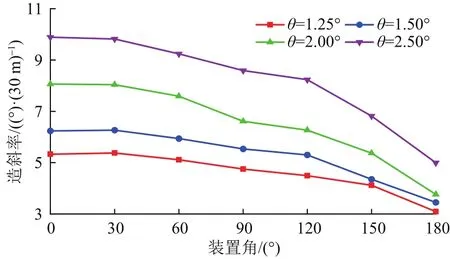
圖6 滑動鉆進時造斜率隨工具面的變化Fig.6 Built-up rate vs.tool face during sliding

3.3 滑動鉆進工具的摩阻影響

結構彎角的增加雖然會增大工具的造斜性能，但過大的彎角會造成BHA在井內難以滑動。圖7為BHA在滑動鉆進過程中鉆壓140 kN、軸向摩阻系數0.7條件下的平均摩阻，通過計算得出，隨著鉆進軌跡的變化、鐘擺效應的逐漸增強，BHA與井壁間產生的平均摩阻增加。結構彎角的增大，加大了BHA與井壁產生的支反力，因此管柱的平均摩阻會隨結構彎角的增加而增加。

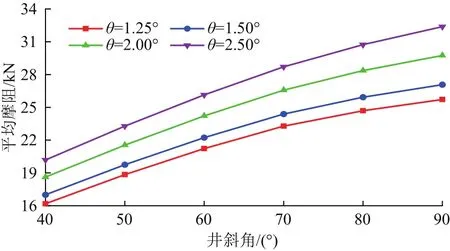
圖7 不同結構彎角下的平均摩阻Fig.7 Average friction vs.structural bend angle

4 結論

(1)針對滑動鉆進過程，基于零側向鉆速準則，建立了滑動鉆進過程中造斜率的計算方法。通過現場實鉆數據進行驗證，其計算值與理論值吻合良好，該方法可為后續的理論研究及實際應用提供依據。

(2)滑動導向模式下，造斜率對工具結構彎角的敏感性大于鉆井參數、軌跡參數及鉆頭側向切削能力的敏感程度。這是因為結構彎角值的增加，明顯加大了杠桿效應，因此在實際鉆進過程中，可根據滑動鉆進過程的特點，合理設計優化工具結構。

(3)在杠桿效應的作用下，鉆壓和井斜角的增加，均有助于提高工具的造斜能力。然而，過高的鉆壓會減弱結構彎角對軌跡的相對作用，過大的井斜角會加大管柱對地層的鐘擺效應，這些因素均會降低工具的造斜能力，其結果對于鉆壓影響而言更為明顯。

(4)隨著工具面由井眼高邊旋轉至井眼低邊，結構彎角上部鉆柱重力對結構彎角處的杠桿效應由加強轉為抑制，因而鉆具的造斜性能會逐漸降低，且結構彎角值越大，造斜率減弱的趨勢越明顯。

(5)在滑動鉆進工況下，不同的結構彎角不僅會影響工具造斜率，也會導致導向鉆具上摩阻的不同。因此，需要綜合考慮工具造斜率、摩阻扭矩等因素的影響，合理地設計工具結構，優化鉆井參數，以充分提高滑動鉆進效率。