基于機器學習的電潛泵工況診斷

王彪 韓國慶 路鑫 譚帥 朱志勇 梁星原

中國石油大學(北京)石油工程教育部重點實驗室

電參數能夠反映電潛泵的實時工作狀態，且容易實現監測和收集，因此在油田開發生產過程中，通過電參數對電潛泵的工作狀況進行監測和分析的研究較多，常見的有電流卡片方法等。這些方法依賴人工經驗，存在人為因素和主觀誤差。使用機器學習算法可以實現電參數的自動分析，提高效率并降低主觀誤差。陳治國等［1］提出了基于模式識別的電流卡片特征值的提取方法，給出了人工判斷的量化指標；余繼華等［2］引入了機器學習，采用神經網絡方法識別電流工況，甘露等［3］使用BP算法對神經網絡進行了進一步擴充；韓國慶等［4］補充了更多工況類別，進一步擴充了神經網絡的適用性；Gupta等［5］使用主成分分析方法討論了電潛泵工況偏離正常狀態時的可視化構建和評判方法；王國輝等［6］基于主成分分析法討論了電潛泵大數據綜合分析預警系統的構建，提出通過對大數據降維實現油井狀態描述和監控預警的方法；隋先富等［7］基于主成分分析法，對電潛泵的多維參數進行降維，通過多維參數監測了電潛泵的工作狀態改變。前人的研究側重于通過某一種方法對電潛泵井的生產狀態進行描述，認識不斷加深，但缺乏從特征提取及處理然后進行分類識別并綜合評價的機器學習完整流程，在不同環節中依然保留有人為因素。本研究在前人研究基礎上，構建了機器學習的完整流程，通過特征工程對波動的電流數據提取大量的特征信息，然后通過降維算法實現特征描述和可視化，再通過分類算法實現工況診斷并給出具體結論，最后進行分析與評價。使用實際生產時的電流數據實例，通過以上4個部分的流程的綜合，實現了對電潛泵工況的快速準確且直觀的描述。

1 電流卡片診斷方法及其改進

電流卡片診斷是API于1982年提出的一種電潛泵故障分類方法，其分類的依據是在不同的工況下運行的電潛泵具有不同的電流波動特征［3］，例如波動的時間長短、波動的頻次大小、電流的峰值與額定值之間的關系等。傳統方法受限于技術條件，通過形態來進行模糊識別，具有較強的主觀因素，在泵工況識別過程中會導致人為誤差［8］。

為了減少誤差，學界進行了多方面的研究，各種傳感器和數據記錄設備的發展，也大大方便了電流參數的量化。傳統的電流卡片記錄分鐘級的電流平均數據，常見的有6 min一個點［9］。隨著傳感設備和數據記錄設備的性能提升，當前油田生產中得到的電流數據可以達到20 s一個點甚至更密。數據記錄密度的提升使得電流記錄可以體現出有關電泵工作狀況的更多信息。此時通過傳統的對電泵工作狀況改變導致電流波動的機理分析就顯得不夠精細和迅速。

數據密度的提升帶來了更多的電流特征。對于分析而言，這些特征的保留使得挖掘更多的信息成為可能。而采用傳統的方法識別，會忽視掉這些特征的細節，這種信息丟失給工況的識別帶來了誤差。經過稀釋的數據可能會淹沒一些關鍵的波動信息，使得一些原本正常的波動變成沒有規律的波動，導致局部的信息丟失和整體的信息變異，其中信息丟失是指局部位置的波動峰值或波動周期的消失，信息變異是指整體的波動形態的改變。此外由于稀釋算法導致的信息損失，可能使得一些原本存在差異的電流波動圖形變得接近，失去其獨特性，從而導致不同工況的電流數據被診斷為同一種工況，影響判斷的準確性。

為了詳細說明局部的信息丟失與整體的信息變異，選取一口氣體影響工況井的20 s一個點的高密度實際電流數據，從中取30 min數據作為研究對象，放大并與一種稀釋算法和一種間歇采樣方法獲得的6 min一個點的稀釋數據進行特征對比。由圖1可看出，高密度實時電流數據反映了某種規律的電流波動，可能與負載的工作情況有關。然而通過傳統的均值方法或間歇采樣得到的低密度電流數據中產生了相比于原始數據的信息丟失，可能導致生產中的某些關鍵信息的損失。

圖1 電潛泵氣體影響工況的高密度實時電流數據與稀釋的電流數據特征對比Fig.1 Feature comparison of high-density real-time current data and diluted current data of ESP under the working condition of gas influence

解決此類信息損失的方法是盡可能保留傳感器設備傳輸的原始密度的數據并進行計算和分析，使用合理的方法去除其中包含的噪聲，同時減少對原始數據的傷害，而非使用其他方法將數據直接稀釋后計算。對于大量數據的處理與分析可以通過使用機器學習方法完成，以實現又快又好的評判效果。

2 機器學習流程

基于電潛泵電流數據的工況識別需要進行包括數據預處理、特征提取、特征降維、分類模型的訓練及預測等流程，方法如圖2所示。

圖2 基于電潛泵電流數據的工況識別流程圖Fig.2 Flow chart of working condition recognition with ESP current data

為了減少數據稀釋帶來的信息損失，需要盡量保留原始的數據密度進行運算。然而更大的數據量導致了計算的困難，也給問題的分析帶來了挑戰，因此需要實施特征工程從原始的波動信息中提取出關鍵的有效信息。

2.1 特征工程

特征工程是指將原始數據轉化為更好地表達問題本質特征的過程，將這些特征運用到預測模型中，能提高對不可見數據的模型預測精度。特征工程的目標是找到分解和聚合原始數據，以更好地表達問題本質的方法，即發現對因變量y有明顯影響作用的自變量特征x。因此，特征工程是數據挖掘模型開發的基礎。

歸一化過程是對原始數據進行線性變化，使結果落到[0,1]區間，以便消除不同數據量級之間的差別，減少分析誤差，轉換函數為

在電潛泵電流分析及工況診斷中，對電流的歸一化數據進行波形分析，得到時域特征和波形特征作為模型的輸入，具體方法如下。

2.1.1 時域特征

(1)特征值1：方差，當前電流值和電流均值之間的偏離程度的度量，定義為

(2)特征值2：均方根值，當一組數據中存在較多0值，即占空比較高時，直接計算其均值不能反映電流強度有效值，均方根值則可以很好地表征電流強度有效值［10］，定義為

(3)特征值3：方根幅值，對振幅的變化非常敏感的物理量［11］，定義為

式中，Ivar為電流方差，A；Ii為當前電流，A；I為電流均值，A；Irms為電流均方根，A；Ir為電流方根幅值，A。

2.1.2 波形特征

(1)特征值4：峰值因數，表示電源系統能夠提供峰值電流能力的指標要求［12］，定義為

(2)特征值5：偏度因子，數據分布偏斜方向和程度的度量，是數據分布非對稱程度的數字特征［13］，負偏度代表統計數據為右偏分布，正偏度代表統計數據為左偏分布，定義為

式中，Cf為峰值因數；Imax為電流最大值，A；Sk為偏度因子。

(3)特征值6：波形因子，用于量化表征波形偏離正弦波形的程度［14］，定義為

其中

(4)特征值7：脈沖因子，用于描述信號沖擊的指標［15］，定義為

(5)特征值8：裕度因子，用來檢測信號中有無沖擊的指標，常用于監測機械設備的磨損狀況［16］，定義為

(6)特征值9：峭度，是反映隨機變量分布特性的數值統計量，可以在頻域內表示一系列瞬態的存在及其位置，消除非平穩信號［17］。定義為

(7)特征值10：峭度因子，表示波形平緩程度，用于描述對振動信號沖擊特性的反映［18］，定義為

式中，Sf為波形因子；Iarv為整流平均值，A；Ii(t)為隨時間變化的電流值，A；Cif為脈沖因子；Cmf為裕度因子；Ck為峭度；Ckf為峭度因子。

通過以上方法對波動的電流數據實施特征工程，即可將波動電流中包含的特征信息盡可能地挖掘出來，以便實施后續的機器學習步驟。特征工程是升維過程，從一維連續時間內的波動中提取出多維特征信息，然后針對這些特征信息展開分析，以數學模型來表達，在特征工程實現過程中提取出的多變量大數據集為研究和應用提供了豐富信息。

2.2 數據降維的聚類算法

在特征工程實現了數據特征的挖掘之后，需要根據挖掘得到的特征值進行處理與分析，處理的過程主要使用聚類算法實現數據降維，以降低計算復雜度。如果采用單獨對每個特征值進行分析的低維度分析方法，則分析往往是孤立的，不能實現數據中信息的綜合利用，盲目減少分析的特征值會損失很多有用的信息，從而給分析帶來誤差。因此需要找到一種合理的方法，在減少需要分析的特征值的同時，盡量減少特征值中所包含信息的損失，以實現對所收集數據的全面分析。常用的數據降維方法有很多，本文采用主成分分析法(PCA)去除數據中的噪聲，降低算法的計算開銷，使得結果更容易可視化并為人所理解［19］。使用主成分分析進行降維是通過線性變化將原始數據變換為一組各維度線性無關的標識，提取數據的主要特征分量。使用主成分分析方法降維可以獲得各主成分的變異系數，將這些變異系數按照主成分繪制為柱狀圖，即為PCA的碎石圖，反映降維后的各主成分所保留的原始信息的百分比。根據可接受的保留信息的比率，通過碎石圖的累積值可以幫助確定所需達到的維度。

降維的維度確定后，就可以將原本多維空間中的點投射到降維形成的主成分空間中，觀察參數的聚集情況。通過對原本數據的所屬工況打上顏色標簽，可以直觀地觀察各工況在主成分空間中是否存在特殊的聚集關系，實現聚類結果的可視化。通過對該聚集關系的描述，就可以進行機器學習的下一步流程，建立實現分類任務的機器學習模型。

2.3 基于邏輯回歸算法(LR)的模式識別

在完成參數的降維、聚類與可視化后，使用分類算法對本研究中的數據聚集情況進行具體的劃分。邏輯回歸是當前業界比較常用的機器學習方法，用于估計某種事物的可能性［20］。它與多元線性回歸同屬一族，即廣義線性模型。多元線性回歸是直接將特征值和其對應的概率相乘得到一個結果，邏輯回歸是在這個結果上加一個邏輯函數，來實現對于事物屬于某一類別的可能性估計。邏輯回歸的主要思想是在模型訓練中，首先得到極大似然函數，然后使用梯度下降法求解函數中參數的近似值。

使用邏輯回歸模型根據一個特征值進行二分類問題求解時，由坐標(x,y)確定的每個點代表一個樣本，其中y值的0和1代表兩種樣本標簽，x代表樣本特征。在分類模型訓練過程中，通過采用不同函數對訓練樣本進行擬合，回歸出一個能夠描述大多樣本特征的函數，該函數就是最終確定的分類模型。對于本任務的多分類回歸問題，使用邏輯回歸模型可以將一個n分類任務拆分為n個二分類任務。某個分類任務歸屬于某種類型，則該類型i對應的第i個混淆特征即為1，其余混淆特征為0，通過對每個混淆特征進行二分類，從而實現多分類。

2.4 機器學習算法的評估方法

在多分類任務完成后，對機器學習算法得到的結果評估是機器學習算法完成后的必要流程。對于多分類任務的評估指標包括準確率(Accuracy)、精確率 (Precision)、召回率 (Recall)、和F1分數 (F1-Score)方法等。根據所要處理的問題不同，各種評估指標具有不同的適用性。

準確率是指對于給定的測試數據集，分類器正確分類的樣本數與總樣本數之比［21］。但當分類任務中不同類型的樣本數量差異比較大時，或者分類任務目標不同，準確率未必能夠真實地反映分類器的分類效果。為了彌補準確率方面的不足，引入了精確率、召回率和F1分數的概念。以二分類任務為例，定義4種分類狀況：真正類(True Positive)、假正類 (False Positive)、假負類 (False Negative)、真負類(True Negative)。

通過以上4種概念定義精確率和召回率。精確

率表示分類器預測為正的樣本中有多少個是真實的正樣本，召回率表示樣本中的正例有多少被正確預測了，兩者分別評判了分類器的漏報或誤報率。精確率和召回率之間是互相影響的，對于一個案例而言，最好的情況是做到兩者都高，但一般情況下精確率高、召回率就低，召回率高、精確率就低。

對于電潛泵的故障診斷而言，既希望召回率高，即減少漏報，避免額外的經濟損失，又希望精確率高，即減少誤報，避免額外的工作量和人力物力投入。因此，精確率和召回率之間還需要一定的平衡。此時就可以使用F1分數來對兩者進行均衡，精確率和召回率越高，則F1分數越高，分類任務越好。

3 案例分析與評價

從A油田電潛泵井數據庫中提取了正常工況、泵抽空、過載停泵、頻繁短周期運行4種工況的井共計56口，使用前文所述特征工程的方法從56口井的實時電流數據中分別提取10個特征值。各樣本井的特征值與工況的對應關系部分示例見表1。

表1 樣本的特征值與工況對應關系的部分示例Table 1 A partial example of the correspondence between eigenvalues and working conditions of samples

利用基于皮爾遜相關系數的相關性分析法對這10個特征值和實際工況進行相關性描述，線性正相關性越強，則相關度越接近1，線性負相關性強，則相關度越接近?1。從圖3各特征值之間的相關關系，以及各特征值與最終工況的相關關系量化可以直觀看出，部分特征值之間存在較強的線性相關性，這說明部分特征值表現的特征是重復的，可以進行適當的降維操作以提取出主要的特征描述方法，降低機器學習的計算量和計算復雜度。且從與工況的關系也可以看出，工況與各個特征值之間均存在較強相關性，這也說明，僅使用單個特征值難以描述對結果的影響。

圖3 各特征值和工況彼此之間的相關系數Fig.3 Correlation coefficients of eigenvalues and the working conditions with each other

基于相關性熱力圖得到的分析結果，其中存在的線性相關性較強的變量需要進行降維以降低計算量并實現可視化。對這些特征值去除工況結論進行無監督的PCA降維聚類，圖4的PCA碎石圖展示了降維的主成分數量保留原始信息的程度，以各主成分解釋的方差比進行量化。

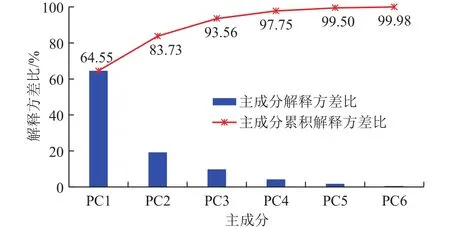
圖4 使用PCA降維的碎石圖和累積分布圖Fig.4 Scree plot and cumulative distribution diagram obtained from dimensionality reduction with PCA

從圖4可以看出，PC1對電流特征值所包含信息的保留程度達到64.55%，PC2對電流特征值所包含信息的保留程度達到19.18%，PC1和PC2共同達到的信息保留程度達到83.73%。兩個主成分就可以保留80%以上的特征值信息，因此從可視化效果以及計算難度上考慮，可以認為使用兩個主成分即可實現對電流特征值的總體描述。

使用降維后的特征值進行二維無監督聚類，觀察數據的聚類情況，以便確定使用電流特征值的二維聚類判別電泵工況的實現可行性。二維無監督聚類效果如圖5所示。

圖5 對電參數特征值進行二維無監督聚類的結果Fig.5 The results of 2-dimensional unsupervised clustering for the eigenvalues of current data

從圖5可以看出，上述56口井在主成分分析圖中似乎有3到4處較好的聚類。為了確定這種聚類方式是否與各個工況相關，用原本各個電流情況對應的工況作標簽來對各聚類點進行顏色和形狀的標記，結果如圖6所示。

圖6 PCA聚類中各點所代表的工況情況Fig.6 The working conditions represented by points in the clustering diagram with PCA

從圖6可以看出，電潛泵的電參數特征值進行二維無監督聚類的位置分布情況確實與不同工況有關，因此認為此次聚類效果較好，實現了各個工況的特征分離。從PCA降維的碎石圖上看，6個維度的主成分能夠描述電流的幾乎99.98%的信息。因此根據PCA算法，形成特征值與主成分的系數矩陣熱力圖，如圖7所示。

圖7 各特征值與各主成分之間的相關系數Fig.7 Correlation coefficients of each eigenvalue with each principal component

圖7中6個主成分與10個特征值的關系的描述為：每一行對應一個主成分，每一列對應一個特征值。以第1行為例，表明第1主成分可使用該行中每格的權重數值與其對應的特征值乘積的累加和表示如下

式中，f1~f10分別表示特征值1至特征值10。

其他主成分的表示方式與第1主成分的表示方式類似。

對主成分與特征值之間關系描述的主要作用是，當新輸入一口井的數據并提取特征值后，按照熱力圖中每個點的系數，即可求取各個主成分值，以便進行后續的機器學習算法。

從圖6的工況分布情況來看，PCA聚類在描述各個電泵工況時具有較好的能力，對于新加入的一口井的數據而言，如果提取特征值并降維后分布位置在上述聚簇內部，那么該井所處工況屬于該聚簇表示的工況的可能性較大，但如果新加入的一口井處于某兩種工況形成的聚簇之間時，對于工況的判別就難以直接描述。此時需要對數據進行機器學習完成分類任務，以進行工況的準確識別和判斷，最終實現機器學習的數據處理、訓練與預測的閉環。

使用邏輯回歸方法對4種工況類型的56口樣本井的數據進行學習和預測，測試集占比設置為30%，計算得到準確率0.84，精確率、召回率和F1分數見表2。

表2 使用邏輯回歸的機器學習的結果評價Table 2 Results evaluation of ML using LR algorithm

如表2所示，模型最終實現的效果中，4種工況類型的56口井的各評價指標評價結果均達到80%以上，且平均F1分數達到了85%，說明使用電流特征值降維的二維主成分建立的邏輯回歸模型在這4種工況類型的56口電泵井的評價中實現了較好的分類效果。

4 結論

(1)與傳統的電流特征識別方法相比，基于機器學習的電潛泵電流分析及工況診斷實現了對電流數據的特征提取，將電流波動的形狀描述問題轉化為基于數據的數學特征量化描述問題，提升了評價的客觀性，減少了人為誤差。

(2)通過特征工程提取的特征值本身復雜多樣，且各個特征值之間可能具有較強的線性相關性，需要對這些數據剔除線性相關變量，保留線性無關變量，以便減少機器學習的輸入數據，降低機器學習的模型復雜度。采用PCA方法降維，一方面保留了特征提取中獲得的主要特征，另一方面減少了機器學習的輸入數據維度，降低了計算復雜度，同時還能通過聚類效果的可視化確定數據特征提取是否滿足泵工況描述的要求。使用二維主成分表征的電潛泵工況信息保留程度達到83.73%，降維聚類表現出了良好的工況區分性，為使用邏輯回歸方法實施分類任務奠定了基礎。

(3)使用降維后的電參數特征數據，建立邏輯回歸模型，完成了對電潛泵工況的診斷。對4種工況類型的56口電潛泵井的診斷準確度、精確度、召回率均達到了80%以上，F1分數達到了平均85%的水平，達到了期望的分類識別效果，實現了有效的電潛泵工況診斷。