動水壓力對深水橋梁單樁地震響應的影響研究

李 芬，彭曉宇，黃蔚源，胡 丹

（1.武漢理工大學船海能動學院，湖北武漢 430063；2.湖北省交通規劃設計院股份有限公司，湖北武漢 430000）

引言

在地震、波浪等復雜環境荷載作用下，流體-結構物-海床相互作用非常復雜，一方面地震荷載引起結構物振動，流體與結構物樁基的動力相互作用會對樁基水下部分產生動水壓力；另一方面海床內部的超孔隙水壓力和土骨架位移表現出周期性和循環累積特性，導致海床土體特性發生變化，影響結構物的抗震性能，因此需要對流體-樁基-海床相互作用展開全面而深入的研究。

目前研究地震動水效應的方法主要包括試驗研究和數值模擬，在試驗研究方面，張士博等［1］開展了斜拉橋橋塔結構在地震、波浪和水流復雜環境荷載作用下的模型試驗，基礎在地震、波浪與水流的作用下忽略了黏滯力相似，采用的彈性力-重力變態相似律，研究表明地震作用對動水壓力的貢獻最大，波浪作用次之，水流影響最小。但是該實驗的模型相似關系因實驗條件的制約進行簡化處理，其精度有待進一步提高。李喬等［2］開展了墩-水耦合振動臺試驗研究，通過附加剛度法沿橋墩高度附加彈簧模擬有水情況的彈性振動問題，研究表明有水環境會改變橋墩的動力性能。文中主要針對深水橋墩動力特性以及動水壓力分布規律，關于樁土作用關系還有待深入考慮。隨著計算機技術的發展，考慮流體與結構物相互作用的流固耦合計算方法、附加質量法或基于規范的弱耦合計算方法成為研究地震動水壓力影響的主要方法。其中附加質量法具有公式簡單、物理意義明確等優點，被廣泛應用于實際工程中，對于橫向小尺寸柱體（樁徑D與波長L之比D/L＜0.2），目前一般采用Morison方程及其修正公式計算地震動水壓力。Morison方程是由Morison等［3］在1950 年提出的半經驗半理論公式，最早被用于計算波、流作用下樁、柱結構的動水壓力，是研究弱耦合領域最具有代表性的成果。廣大學者基于Morison 方程研究了動水壓力對橋墩等結構物地震響應的影響，如李忠獻等［4］通過實驗考慮了水-振動臺相互作用，分析了動水附加質量在不同激勵條件與水深下的變化規律，研究表明激勵作用與水深對動水附加質量的影響較大。袁迎春等［5］研究了Morison方程中阻尼力對圓截面樁地震反應的影響，研究表明在深水橋梁基礎的抗震計算中可以忽略阻尼力。Yang等［6］基于水平振動的橋墩及其周圍流場具有雷諾數高、Keulegan-Carpenter 數小等特點，基于理論推導和數值計算說明了慣性力占主導地位，阻尼力可忽略不計。高學奎等［7］基于Morison 方程計算地震動水壓力，研究表明地震動水壓力增大了橋墩結構的動力響應。Penizen 等［8］基于Morison 方程計算動水壓力，采用隨機地震響應分析方法研究了強震作用下近海塔架結構的動力響應。李悅等［9］在Morison 方程的基礎上提出了適用于深水大跨徑斜拉橋動力時程響應分析的動水壓力簡化計算方法。冼巧玲等［10］基于Morison 方程討論了水深變化對橋梁動力特性的影響以及地震動分別沿順橋向和橫橋向輸入時對橋梁地震響應的影響程度。

上述研究為了簡化計算，往往忽略了樁-土相互作用，黃信等［11］研究表明考慮橋墩-土相互作用時，地震動水壓力對樁基橋墩地震響應的增幅明顯減小，但其影響仍不容忽視。劉紅彪等［12］采用數學理論推導與動力時程仿真計算相結合的方式對高樁碼頭結構的變形位移進行研究，結果表明樁-土相互作用對軟土地基上高樁碼頭結構的動力響應有較大影響，不考慮樁-土相互作用的變形位移偏小，結果偏于不安全。Yamada 等［13］采用頻域分析方法研究了在隨機波浪和地震作用下近海結構物的動力響應，指出相對于剛性地基而言，考慮土-結構物相互作用使得結構物的振動頻率減小、輻射阻尼降低、響應偏大。趙秋紅等［14］對深水橋墩地震響應的研究現狀進行了總結，指出了考慮深水橋梁下部結構與土的相互作用時，影響了動水壓力的分布以及橋墩的地震響應。Damagaard 等［15］進一步指出按照傳統設計方法，如采用Winkler地基梁模型、p-y曲線等離散模型描述樁-土相互作用時，近海結構物的固有頻率計算值往往偏小，且有必要將海床作為飽和多孔介質，即考慮超孔隙水壓力的影響。文中將土體軟化參數引入等效黏彈性模型中，建立了循環次數與軟化指數相結合的指數關系式，提出了考慮土體動應力-應變非線性、滯回性以及循環軟化特性的飽和軟黏土剛度衰減模型。進一步基于動三軸試驗結果確定飽和軟黏土的動力特性參數和軟化特性參數，基于FLAC3D 進行二次開發實現了該修正模型，與動三軸試驗結果和離心機試驗結果對比驗證了該模型能有效地模擬飽和軟黏土在循環荷載作用下的剛度衰減，為研究近海結構物在地震、波浪等循環荷載作用下的動力響應提供了基礎。

文中將采用飽和軟黏土剛度衰減模型描述循環荷載作用下海床土體特性的變化，建立考慮地震動水壓力的飽和海床-樁基動力相互作用數值模型，探討地震動水壓力對樁基動力響應的影響；并進一步討論樁基入水深度、海床厚度和地震烈度等因素對流體-樁基-海床相互作用機制的影響。

1 樁基-海床相互作用數值模型

1.1 飽和軟黏土剛度衰減模型

在地震和波浪等循環荷載作用下，超孔隙水壓力累積上升、有效應力降低、主應力大小和方向不斷改變進一步引起了土體的破壞和結構重塑，對于軟黏土海床主要體現為強度和剛度的降低，工程上一般稱之為循環軟化。

文中采用S 曲線模型擬合了Kaolin 飽和軟黏土的模量衰減-動剪應變關系曲線、等效阻尼比-動剪應變關系曲線，S曲線模型的表達式為：

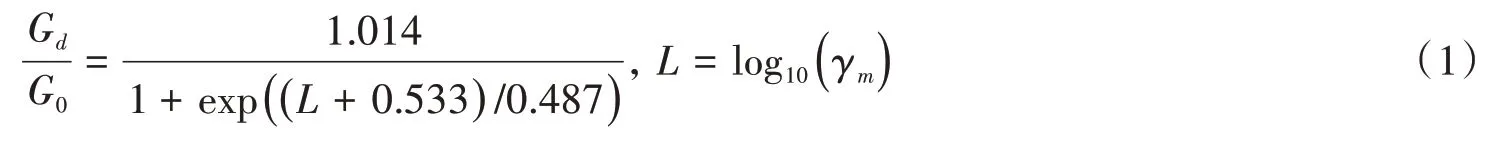
式中：G0為初始剪切模量；γm表示循環剪切應變幅值。

Idriss等［16］提出了用軟化指數δ描述土體模量的衰減，Baneerje等［17］基于應變控制的循環動三軸試驗，引入軟化參數t建立了軟化指數δ和循環次數N的指數關系式，

式中：GsN和Gs1分別表示第N次和第1 次循環的割線剪切模量；τcN和τc1分別表示第N次和第1 次循環的剪切應力幅值。

文中通過FLAC3D 預留的UDM 程序接口，應用Visual C++編譯DLL 動態鏈接庫文件，在FLAC3D 框架內實現了飽和軟黏土剛度衰減模型的二次開發［18］。如圖1所示，基于FLAC3D得到的S曲線模型的擬合曲線與動三軸試驗結果基本吻合［15］；圖2表明式（2）能基本擬合Idriss試驗曲線。

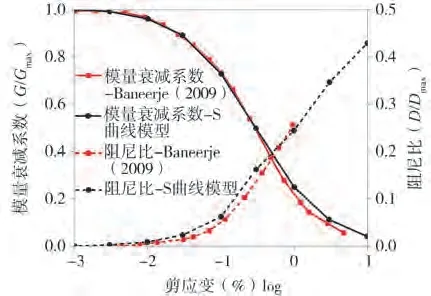
圖1 模量衰減和等效阻尼比擬合曲線與試驗結果對比Fig.1 Comparison of the measured results with the fitted modulus degradation and the equivalent damping ratio curves

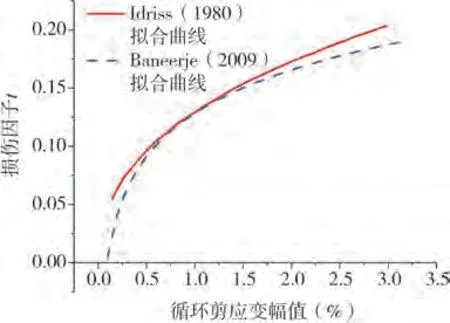
圖2 損傷因子擬合曲線與試驗結果對比Fig.2 Comparison of the measured results with the predicted damage parameter

1.2 數值模型

目前描述海床土體動力特性的多孔連續介質模型主要包括Biot 理論和TPM 理論，文中將基于Biot 理論的簡化形式“SD”［19］建立海床動力模型。在數值模擬中，單樁基礎的單元形式主要包括實體單元和結構單元，實體單元能夠真實模擬樁基的截面特性，但無法直接獲取沿樁身的剪力和彎矩分布；結構單元可以直接反映樁基的剪力和彎矩響應，卻無法描述樁基的真實截面，文中將采用混合單元法模擬樁基，即首先建立能描述樁基真實截面特性的實體單元，再沿實體單元的中心軸線建立結構單元。

樁基-海床相互作用體系非常復雜，涉及到樁基和土體的材料非線性和幾何非線性，以及樁-土接觸面的接觸非線性。如圖3所示為流體-樁基-海床動力相互作用示意圖，樁埋置在海床中，海床厚度為h，樁基入土深度為H，水深為d，地震動水壓力在沿樁基入水部分均勻分布。文中采用無厚度接觸面單元描述樁-土之間可能出現的分離、滑移或閉合，樁-土接觸面的正應力和切應力平均分配在接觸面各節點上。如圖4所示為樁基-海床相互作用數值模型，模型的長、寬、高均為30 m，圓截面樁基的直徑為3 m、高40 m，樁入土深度為20 m，入水深度為10 m，在靠近樁體部分的網格加密，網格大小隨深度遞減，模型的單元總數為25 080，節點總數為28 252，模型的基本參數見表1。關于模型的邊界問題文中采用了針對飽和軟黏土提出的結合地震動輸入的DRM 方法［18］，該方法可以精確描述外部激勵，能夠將外源激勵轉化為等效力施加在模型內部的虛擬邊界面上，且該方法在考慮材料非線性時，不需要對整體模型進行非線性分析，通過建立自由場模型，計算等效地震力，再將等效地震力輸入模型的內部邊界的方式實現。該方法可以縮小建模區域，提高了計算效率及計算精度。通過比較FLAC3D 中不同邊界條件模擬的矩形隧道的地震響應，檢驗了這種高精度吸收邊界的性能。Dan Hu等［18］通過地震離心機實驗證明其結果與相應的實驗吻合，并通過數值分析結果表明，這種吸收邊界可以有效地用于基于飽和多孔介質的結構動力分析。

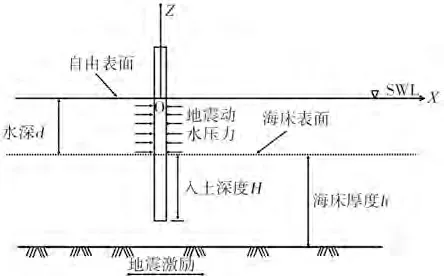
圖3 地震荷載下流體-樁基-海床動力相互作用示意圖Fig.3 The sketch of fluid-pile-seabed dynamic interaction under earthquake loadings

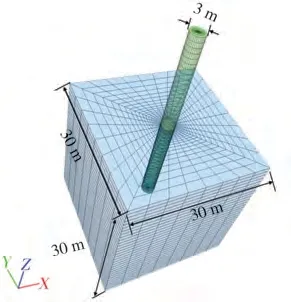
圖4 海床-單樁相互作用數值模型Fig.4 The numerical modelling of seabed-monopile interaction

表1 數值計算參數Table 1 The numerical parameters

2 地震作用下動水效應影響研究

袁迎春等［5］和Yang等［6］研究表明采用Morison方程計算作用于水平振動橋墩的地震動水壓力時，慣性力占主導地位，阻尼力可忽略不計。因此，文中在計算地震動水壓力時，忽略了Morison 方程中阻尼力的影響。采用數值方法研究樁基-海床相互作用時，首先對樁基進行空間離散化處理，將地震動水壓力以附加質量的形式施加在樁基入水部分各截面的節點上。

式中：A表示結構物在i節點處的橫截面積；li表示劃分的單元長度，結構物上第i個節點的附加質量為i節點上下單元各一半的附加質量之和；CM表示附加質量，文中依據《海上移動式鉆井船入級與建造規范》選取圓截面樁的慣性系數為CM=2.0。

文中選取了3 列地震波，并討論在不同地震動輸入下，動水壓力分別對樁基位移、剪力和彎矩的影響。如圖5所示為Chichi、Kobe和Loma Prieta 3條地震動的加速度時程曲線，地震波的時長為40 s。

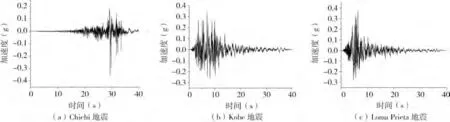
圖5 地震動加速度時程曲線Fig.5 The acceleration time history of the earthquake input motions

2.1 樁基位移反應

在地震動響應分析中，工程持時應包含地震記錄最強烈的部分，時長一般為基本周期的5～10 倍，且大于12 s。文中Chichi地震、Kobe地震和Loma Prieta地震作用下的時程響應曲線分別為40 s、20 s和18 s。

圖6（a）～（c）為不同地震激勵下，考慮動水壓力和不考慮動水壓力的樁頂位移時程曲線。對比可知，在Chichi 地震激勵下，動水壓力對樁頂位移時程曲線幾乎無影響；在Kobe 地震激勵下的前15 s 內動水壓力的影響不顯著，15 s后樁頂位移增大，位移增長不超過位移峰值的12%；在Loma Prieta地震激勵下，7.5 s后動水壓力的影響增強，但位移增值不超過位移峰值的9%。

圖6 不同地震激勵下樁頂位移時程曲線Fig.6 The time history of pile displacement under earthquake motions

圖7（a）～（c）對比了不同地震激勵下，動水壓力對沿樁身水平位移峰值的影響，標高為0 m、20 m、30 m和40 m的位置分別對應著樁底、水-土接觸面、自由水面和樁頂。在Chichi地震激勵下，動水壓力對沿樁身水平位移峰值的影響很小，樁頂位移峰值的增幅為1.2%；在Kobe 地震激勵下，動水壓力對沿樁身水平位移峰值幾乎無影響；在Loma Prieta地震激勵下，動水壓力使得樁基出水面部分（z＞30 m）的水平位移峰值增加，樁頂位移峰值的增幅為3.2%。

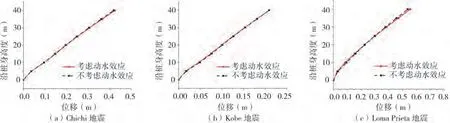
圖7 不同地震激勵下沿樁身水平位移峰值分布Fig.7 The maximum horizontal displacement along pile depth under earthquake motions

由上述對比可知，動水壓力對樁基水面以下部分（z＜30 m）的位移峰值幾乎無影響，但樁基出水面部分（z＞30 m）的位移峰值變大；且動水壓力對位移反應的影響程度與地震動特性有關，依據動水壓力對位移反應的影響程度，Loma Prieta地震＞Kobe地震＞Chichi地震。

2.2 樁基剪力反應

圖8（a）～（c）對比了不同地震激勵下的樁底剪力時程曲線，在Chichi地震激勵下，考慮動水壓力對樁底剪力時程曲線幾乎無影響；在Kobe地震和Loma Prieta地震激勵下，從出現剪力峰值時刻開始，樁底剪力出現了較顯著的增長，Loma Prieta地震激勵下的剪力增幅達15%。

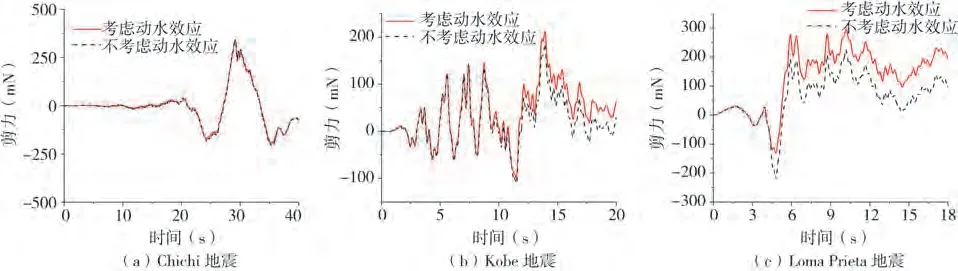
圖8 不同地震激勵下樁底剪力時程反應Fig.8 The time history of shear stress at pile bottom under earthquake excitations

圖9（a）～（c）比較了在不同地震激勵下沿樁身剪力峰值分布，對比可知動水壓力對水-土接觸面以上部分（z＞20 m）的樁基剪力峰值幾乎無影響；埋入土層深度5 m 以下部分（z＜15 m）的剪力峰值出現差異，最大差值出現在樁底。

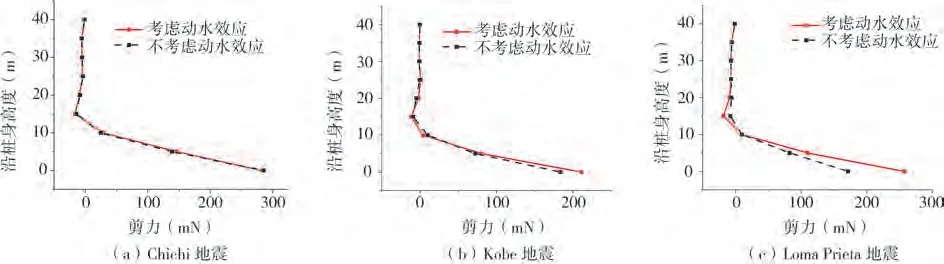
圖9 不同地震激勵下沿樁身剪力峰值分布Fig.9 The distribution of the maximum shear stress along pile depth under earthquake excitations

由上述對比可知，動水壓力主要對埋置在土層內的樁身剪力產生影響，且沿埋入深度其影響更為顯著；一般從出現剪力峰值時刻開始，動水壓力對剪力的放大作用增強。同樣地，動水效應對剪力反應的影響程度也與地震動特性有關，依據剪力峰值的增幅大小，Loma Prieta地震＞Kobe地震＞Chichi地震。

2.3 樁基彎矩反應

如圖10（a）～（c）所示，在Chichi 地震激勵下，動水壓力對樁底彎矩時程幾乎無影響；而在Kobe 地震和Loma Prieta地震激勵下，動水壓力使得樁底負彎矩變大，體現了動水壓力對樁底的負彎矩效應。

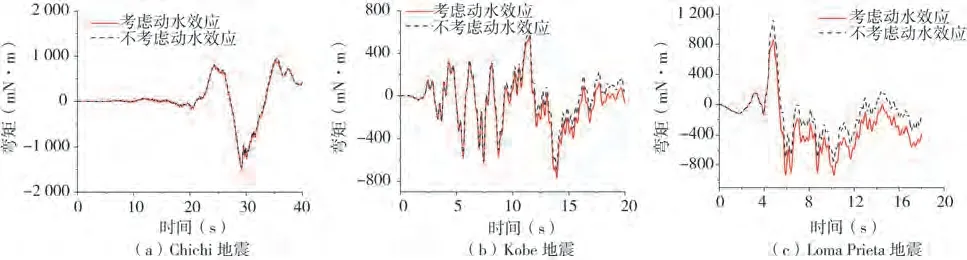
圖10 不同地震激勵下樁底彎矩時程反應Fig.10 The time history of bending moment at pile bottom under earthquake excitations

如圖11（a）～（c）對比了不同地震激勵下動水壓力對沿樁身彎矩峰值的影響，在Chichi地震激勵下，動水壓力對埋入土層內（z＜20 m）的彎矩峰值幾乎無影響，土層表面以上（z＞20 m）的彎矩峰值增大，土層表面處的彎矩增長（z=20 m）為樁底彎矩峰值的6.7%；在Kobe 地震激勵下，彎矩的差異主要出現在樁基入土部分，樁底彎矩峰值增長約10%；在Loma Prieta 地震激勵下，動水壓力對沿樁身彎矩都有影響，樁底彎矩峰值減小約24%。

圖11 不同地震激勵下沿樁身彎矩峰值Fig.11 The maximum bending moment along pile depth under earthquake excitations

動水壓力對沿樁身彎矩峰值的影響程度、影響范圍與地震動特性有關。依據彎矩峰值的增幅大小，Loma Prieta 地震＞Kobe 地震＞Chichi 地震；動水壓力對彎矩的影響主要體現為正方向彎矩減小，負方向彎矩增大。

2.4 影響系數

為了量化動水壓力對樁基動力響應的影響，定義動水壓力的影響系數Rx為：

RD，RS，RM分別代表動水壓力對樁頂位移、樁底剪力和樁底彎矩峰值的影響系數，不同地震激勵下動水壓力對樁基位移、剪力、彎矩的影響系數見表2。

表2 不同地震激勵下動水壓力的影響系數Table 2 The influence factor of hydrodynamic pressure under different earthquake input motions

由表2 可知，相較于無水環境下，考慮動水壓力時樁基的動力響應變大，而動水壓力的影響程度與地震動特性相關。具體來說，Chichi 地震激勵下動水壓力影響不顯著，位移影響系數最大，僅為1.2%；Kobe 地震激勵下動水壓力對剪力和彎矩影響較為顯著，分別為15%和10%；Loma Prieta 地震激勵下動水壓力對剪力和彎矩的影響最為顯著，增幅分別為15%和32%。

3 參數分析

本節將討論在不同水深、土層厚度和地震烈度下，動水壓力對樁基動力響應的影響。由于樁基的位移、彎矩對樁基的合理設計十分重要，本節將主要探討在Kobe 和Loma Prieta 地震激勵下，不同參數對沿樁身位移和彎矩峰值的影響。

3.1 水深影響

《水運工程抗震設計規范》（JTS 146-2012）中規定了考慮動水壓力的最小深度為5 m，文中定義相對水深為水深與樁長的比值，選取水深d為0 m、10 m、15 m 和20 m，樁長為40 m，則相對水深分別為0、0.25、0.375 和0.5。

為了量化描述水深對樁基動力響應的影響，將計算不同水深條件下樁基位移、彎矩峰值的影響系數。由表3 可知，隨著水深的增加，樁頂位移和沿樁身彎矩峰值都有不同程度的增加，表明水-結構物相互作用的影響更為顯著；動水壓力對彎矩的影響程度顯著大于對位移的影響程度，如在Loma Prieta 地震激勵下，當相對水深為0.5，即樁基完全沒入水中時，位移和彎矩的最大響應增幅分別為4.3%和36.8%。因此，在開展深水橋梁樁基的抗震設計時，需要考慮動水效應對樁基彎矩的影響。

表3 水深變化對樁基位移和彎矩峰值的影響Table 3 The effect of water depth variation on the pile displacement and bending moment

3.2 土層厚度影響

圖12（a）～（b）對比了在不同地震激勵下，分別考慮動水壓力和無水條件下，土層厚度對樁頂位移峰值、樁底彎矩峰值的影響。在Kobe 地震作用下，土層厚度從30 m 增加至50 m，樁基位移先增加后減小，樁基彎矩變大，如考慮動水壓力的位移峰值和彎矩峰值增幅分別為52%和11.5%，無水情況下的位移峰值和彎矩峰值增幅分別為50%和16.7%。在Loma Prieta 地震作用下，土層厚度從30 m 增長至50 m，樁基位移和彎矩變大，如考慮動水壓力時的位移和彎矩峰值增幅分別為23.2%和20%，無水情況的位移和彎矩峰值增幅分別為23.6%和49.4%。隨著土層厚度的增加，樁基位移和彎矩峰值顯著增長，動水壓力的影響不容忽視。

圖12 土層厚度對樁頂位移峰值和樁底彎矩峰值的影響Fig.12 The effect of seabed depth on the maximum displacement at pile tip and bending moment at pile bottom

3.3 地震烈度影響

將地震烈度進行量化的物理量主要包括加速度峰值、速度峰值、位移峰值、地震波能量或反應譜等。依據《水運工程抗震設計規范》，抗震設防烈度和設計基本地震加速度值的對應關系見表4。

表4 抗震設防烈度和設計基本地震加速度值的對應關系Table 4 The relationship between the earthquake fortification intensity and the designed acceleration amplitude

文中采用加速度峰值作為衡量地震烈度的尺度，原始地震動的地震烈度為8 度；將原始Kobe 地震和Loma Prieta地震的加速度幅值分別縮小2倍和10倍，加速度幅值分別為0.172 g和0.034 5 g，對應的地震烈度分別為6度和7度。

圖13（a）～（b）分別描述了樁頂位移峰值和樁底彎矩峰值隨地震加速度幅值的變化，Kobe地震加速度幅值從0.034 5 g增長至0.345 g，考慮動水壓力時位移和彎矩峰值分別放大了12.45倍和7.25倍，無水條件下的位移和彎矩峰值分別放大了12.66倍和6.85倍。Loma Prieta地震加速度峰值從0.034 5 g增長至0.345 g，考慮動水壓力的位移和彎矩峰值分別放大12.8倍和7.15倍；無水條件下的位移和彎矩分別放大12.4倍和5.48倍。

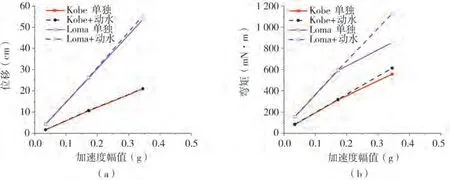
圖13 地震烈度對樁頂位移峰值和樁底彎矩峰值的影響Fig.13 The effect of seismic intensity on the maximum displacement at pile tip and bending moment at pile bottom

在6度和7度地震作用下，動水壓力對樁基位移和彎矩無影響；在8度地震作用下，考慮動水壓力使得樁基位移和彎矩變大，且動水壓力對樁基彎矩的影響更為顯著。隨著地震烈度的增加，考慮動水壓力時，位移和彎矩呈線性增長關系；不考慮動水壓力時，位移和彎矩的增長變緩，且樁頂位移峰值放大系數大于樁底彎矩峰值放大系數。

4 結論

（1）考慮動水壓力使得樁基動力響應增大，主要包括樁基位移、剪力和彎矩，動水壓力對樁基的影響程度與地震動特性有關，一般在頻率較低（1～5 Hz）、烈度較大的地震激勵下，動水壓力的影響更為顯著。

（2）動水壓力對樁基彎矩的影響最為顯著，依次為剪力和位移。一般來說，考慮流體-結構物相互作用使得樁基出水面部分的位移增長，埋置在土層內的樁身剪力增大，樁底負彎矩增大。在進行近海結構物樁基設計時，需要設計人員重點關注。

（3）動水壓力隨著水深、土層厚度以及地震烈度的增加使得樁基位移和彎矩受到影響：水深對彎矩的影響程度更大，如樁基完全沒入水中的位移和彎矩最大響應增幅分別為4.3%和36.8%；土層厚度的影響相較于水深更為顯著，考慮動水壓力和不考慮動水壓力時的彎矩峰值增幅分別為20%和49.4%；地震烈度僅在較大情況即達到8 級時，樁基的位移和彎矩都出現了顯著增長，如在Loma Prieta 地震激勵下，位移和彎矩峰值分別放大12.8倍和7.15倍。因此，在開展深水橋梁樁基的抗震設計時，動水壓力對樁基彎矩的影響不容忽視。