考慮初始幾何缺陷的大跨管桁架屋蓋非線性穩定性研究

馬志海毛小勇黎明劉聰，*

（1.中鐵建設集團有限公司，北京 100040；2.蘇州科技大學土木工程學院，蘇州 215004）

0 引言

為滿足大跨度公共建筑對跨度和造型的要求，諸如網架、網殼、桁架、懸索等結構形式獲得大量應用［1］。相對其他鋼結構形式，管桁架結構具有構造簡單、結構外形簡潔、可滿足各種不同建筑形式的要求，特別是拱形和各種曲線形式［2］。管桁架的結構體系一般為平面或空間桁架，在節點處采用桿件直接焊接的相貫節點［3-4］。對于相貫節點，在同一軸線上的兩個主管貫通，其余桿件通過端部相貫線加工后，直接焊接在貫通桿件的外部。目前此類結構多用在機場、體育場和會議中心等公共建筑中。

穩定性分析是管桁架結構設計中的重要環節，鑒于較小的管截面和結構尺寸，局部失穩、平面外失穩和整體失穩都有可能發生［5-7］。管桁架結構多采用分段施工，通過吊裝焊接實現整體結構的搭建，考慮到施工精度，焊接和吊裝的過程都會使結構產生一定的幾何缺陷，特別是對于大跨度結構，因此在管桁架結構穩定性分析中，必須考慮幾何缺陷的影響［8-11］。在鋼結構分析中，一般需考慮兩種幾何缺陷：①構件的初彎曲；②結構的初偏移。在考慮缺陷的鋼結構穩定性分析中，主要包含缺陷幅值和分布模式。

在大跨度結構分析中，缺陷分布模式主要采用一致缺陷模態法和隨機缺陷模態法［12］。在一致缺陷模態法中，首先對結構進行線彈性屈曲分析，然后將第一階屈曲模態乘以比例系數作為結構的幾何缺陷，該方法假定結構的第一階屈曲模態與最終失穩模態相同［13-15］。在《空間網格結構技術規程》中，規定了需采用一致缺陷模態法對網架結構進行穩定性分析，對缺陷幅值和穩定系數也有相應要求［16］。然而，管桁架結構在節點和桿件布置形式以及加工和施工方式上都有較大差異，進而導致缺陷形式亦有較大不同，且已有研究表明，結構最終失穩模態可能不同于第一階屈曲模態。Silveria Alvarenga［14］將彈塑性二階分析獲取的破壞模式作為幾何缺陷的分布模式，其結果過于保守。因此，需對幾何缺陷對管桁架結構穩定性的影響做進一步研究。

本文以鹽城體育館交錯管桁架屋蓋工程為背景，重點研究初始幾何缺陷對交錯管桁架穩定性的影響。首先建立大跨交錯管桁架的三維有限元模型，然后開展結構的線性屈曲分析，獲取結構前三階模態。為獲取該結構的穩定承載力，驗證結構的安全性，對結構進行非線性屈曲分析，鑒于相關規范中缺乏對大跨度交錯管桁架幾何缺陷的明確規定，本文聚焦于缺陷模式和缺陷幅值對結構非線性穩定承載力的影響研究，選取線性屈曲分析中得到的不同模態及其組合形式，針對不同缺陷幅值，以得到綜合的安全性保證，最后給出相應的穩定性設計建議。

1 結構數值模型建立

本文涉及工程為鹽城體育館大跨屋蓋，采用交錯桁架結構體系，底部支撐為鋼筋混凝土結構，桁架平面尺寸為135.5 m×103.3 m，相對高度為3.96 m，主桁架跨度77.4 m，桁架鋼管最大規格為Φ450×20 mm，最小規格為Φ159×8 mm，結構效果圖如圖1所示。構件材質均采用Q345B鋼材，屈服強度345 MPa，極限強度550 MPa，極限應變0.2。桁架桿件間通過相貫面焊接連接，采用分段吊裝。結構屋面采用1.1 mm厚直立鎖邊鋁鎂錳金屬板，隔熱隔音層采用100 mm后巖棉氈。考慮上人檢修荷載，統計得均布荷載標準值為3.0 kN/m2，穩定性驗算中，將均布荷載集中至節點處。

圖1 體育館鋼屋蓋效果圖Fig.1 Rendering of steel roof of gymnasium

本文采用ABAQUS對結構進行穩定性分析，整體模型采用B31梁單元，屋蓋底部局部節點處采用柱支撐，有限元模型及支座布置情況如圖2所示，采用三向鉸接處理。在結構施工過程中，采用全站儀對屋蓋中心位置處進行了分階段的位移監測，如圖3（a）所示，得到管桁架施工完成到上下覆板施工完成期間，結構中心位置處沉降約6 mm。為驗證模型的準確性，將上下覆板自重荷載施加至結構上，通過計算得到結構中心位置處位移為6.47 mm，如圖3（b）所示，與實測結果較為接近。

圖2 大跨交錯桁架屋蓋數值模型與支座布置Fig.2 Numerical model and support arrangement of long-span staggered truss roof

圖3 數值模型準確性驗證Fig.3 Accuracy verification of numerical model

在穩定性分析中，首先進行結構的線性屈曲分析，得到模型的屈曲特征值與屈曲模態，然后引入初始幾何缺陷對結構進行非線性彈塑性全過程分析，獲取結構的失穩模式和穩定承載力，并對缺陷模式和幅值對穩定承載力的影響進行研究。

2 線性屈曲分析

線性屈曲分析主要針對線彈性材料且非線性效應不明顯的結構。通過線性屈曲分析，可獲得結構的屈曲特征值及屈曲模態。本文主要獲取結構前三階屈曲模態作為結構的初始缺陷模式。通過模型計算，得到結構的前三階屈曲模態，如圖4所示。由圖可知，結構第一階屈曲模態表現為中部桁架的平面外失穩，不同于一般網架、網殼類結構，此結構上下弦間距達4 m，易發生平面外的局部失穩。結構第二階屈曲模態表現為整體結構向上的豎向變形，具有一定的拱效應。結構第三階屈曲模態表現為中部一半凸出、一半凹陷。由于圖4（c）水平支撐的設置，整體結構剛度分布不均，結構中部沿縱向被分成兩塊剛度較弱區域，其中一塊向上凸出、另一塊向下凹陷。

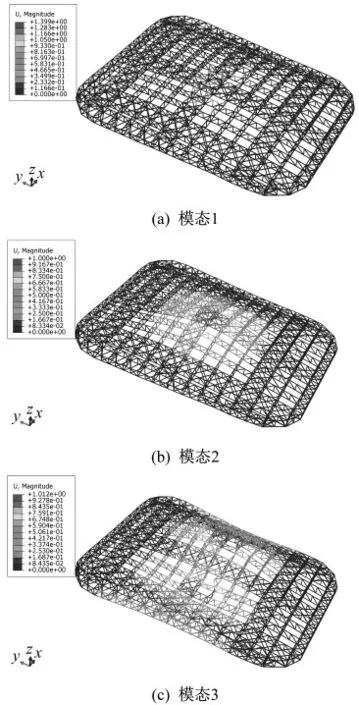
圖4 大跨交錯桁架屋蓋前三階屈曲模態Fig.4 First three order buckling modes of long-span staggered truss roof

3 缺陷影響分析

非線性屈曲分析可將材料非線性和結構的初始幾何缺陷考慮在內，本文采用“一致缺陷模態法”模擬結構的初始缺陷，分析過程中考慮幾何大變形的影響。本文所研究交錯桁架結構具有跨度大、桿件多的特點，在焊接和分塊吊裝過程中，不僅容易產生局部變形，也會使得變形累計導致整體缺陷過大的情況，除在施工過程中提高精度外，尚需研究不同缺陷對結構整體穩定性的影響。為此，本文將結構三種屈曲模態及其組合形式作為缺陷模式，令缺陷幅值從0.1～0.7 m每間隔0.05 m取值，可得荷載比例因子λ隨缺陷幅值v的變化關系如圖5所示。由圖可知，除缺陷模式為第三階屈曲模態、缺陷幅值為0.7 m的模型外，其余模型的比例因子都在2.0以上。當缺陷幅值為0.1 m時，前三階屈曲模態對應的比例因子呈漸次降低的趨勢。隨著缺陷幅值的增大，第一階和第三階屈曲模態對應的比例因子呈下降趨勢，第二階屈曲模態對應的比例因子呈上升趨勢，主要是由于初始缺陷為結構中部的向上凸出，而隨著荷載的增大，這部分變形要被抵消掉。當缺陷幅值超過0.4 m后，缺陷模式為第一階屈曲模態對應的比例因子下降迅速，主要是由于第一階屈曲模態為局部的平面外失穩，受缺陷幅值的影響較大。整體來看，由第三階屈曲模態計算所得比例因子皆小于第一階屈曲模態對應比例因子，因此，對于大跨度交錯桁架結構，只驗算第一階屈曲模態對應的穩定承載力是不安全的。

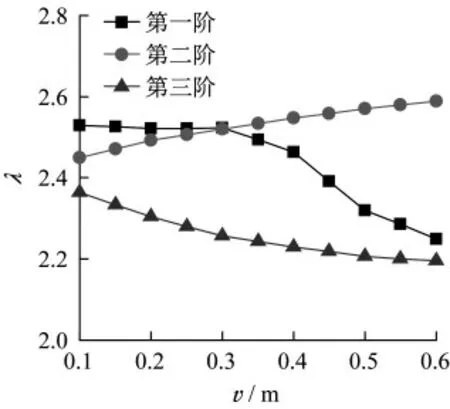
圖5 不同缺陷模式下比例因子隨缺陷幅值變化關系Fig.5 Relationship between scale factor and imperfection amplitude in different buckling modes

當缺陷幅值為0.3 m時，第一階屈曲模態和第二階屈曲模態對應的比例因子近似相等，圖6給出了二者最終的失穩模式，從圖中可看出，對于第一階屈曲模態，受初始幾何缺陷的擾動，失穩時中部上弦桿和水平支撐應力和變形較大，而對于第二階屈曲模態，結構縱向支座處腹桿應力較大，中部桿件應力較小。

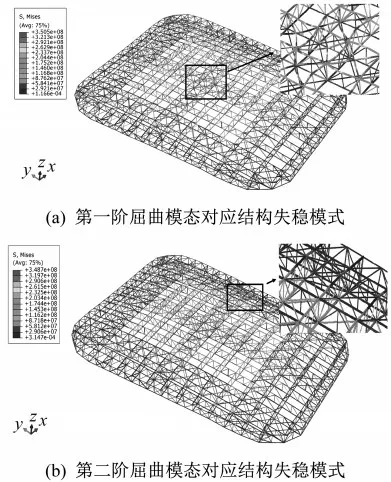
圖6 缺陷模式為第一階和第二階屈曲模態時結構非線性失穩模式Fig.6 Nonlinear buckling modes of structures in first-and second-order buckling modes

部分文獻將結構前三階模態按照一定比例組合作為結構的初始幾何缺陷，本文按0.6，0.2，0.2的比例對前三階模態進行組合，以研究模態組合下初始幾何缺陷對結構穩定承載力的影響［17］。所計算模型包含A、B兩組，每組11個，具體參數見表1，所得比例因子如圖7所示。

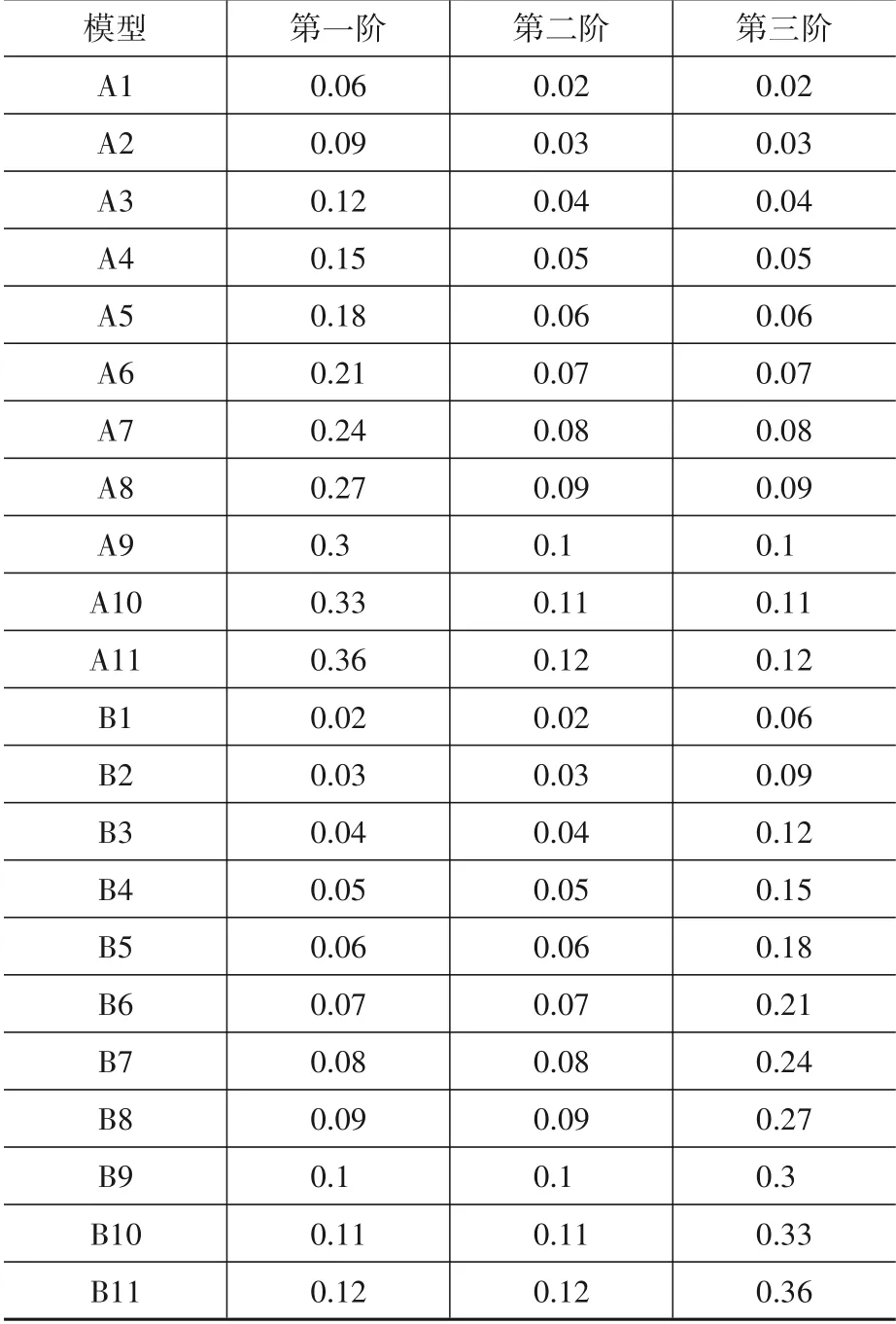
表1 前三階屈曲模態組合時缺陷幅值設置Table 1 Imperfection amplitude setting in combination of the first three buckling modes

由圖7可知，對于A組模型，隨缺陷幅值的增大，比例因子整體呈上升趨勢，而B組模型的比例因子逐漸下降，而且兩組模型比例因子的差值逐漸增大。對比圖5和圖7，當采用前三階屈曲模態的組合作為缺陷形式，缺陷對結構穩定承載力的影響降低了。對于A組模型，以第一階屈曲模態為主（0.6的比例），但整體趨勢與第二階屈曲模態對應的比例因子變化趨勢類似；對于B組模型，以第三階屈曲模態為主，其整體趨勢與第三階屈曲模態對應的比例因子變化趨勢基本相同。由此可知，當采用前三階屈曲模態組合時，第三階屈曲模態對整體穩定承載力的影響最大，第一階屈曲模態的影響最小，因此，對結構整體穩定承載力來說，局部的幾何缺陷對穩定承載力的影響要小于整體的幾何缺陷，雖然結構第一階屈曲模態為局部中心桿件的變形。綜合以上分析，對于本文涉及的大跨度交錯桁架結構，由于桿件截面設置和結構尺寸的要求，由線性屈曲分析得到的屈曲模態既有桿件的局部失穩，也有結構的整體失穩，直接將結構的第一階屈曲模態作為初始幾何缺陷的缺陷模式是不穩妥的。由于結構起拱效應，所得屈曲模態中存在中部向上凸出的模態，此時缺陷對結構的穩定承載力是有益的，應避免將此模態作為缺陷模式。相比單模態形式，采用多模態組合形式，缺陷對結構穩定承載力的影響降低了。對于本文的結構形式，應采用第三階屈曲模態作為缺陷形式，對于缺陷幅值，依據本文從0.1 m至0.6 m多模型計算，結構荷載比例因子皆大于2.0，因此本結構穩定性驗算滿足要求。

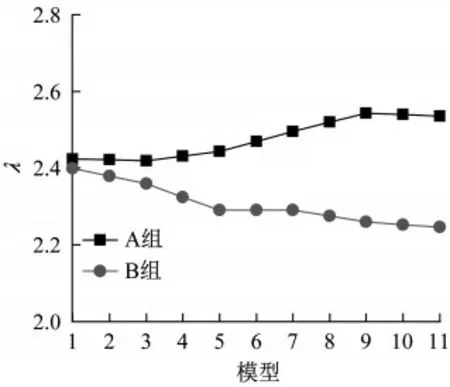
圖7 前三階屈曲模態按不同比例組合時比例因子變化情況Fig.7 Variation of scale factors with combinations of the first three orders of buckling modes according to different proportions

4 結論

本文以鹽城體育館大跨度交錯管桁架屋蓋工程為研究背景，針對該結構穩定性分析中的初始缺陷引入問題進行研究。首先采用ABAQUS建立結構三維非線性有限元模型，然后開展線性屈曲分析和考慮材料非線性和初始幾何缺陷的非線性全過程分析，研究不同缺陷模式和缺陷幅值對結構穩定承載力的影響，可得以下結論：

（1）對于大跨度交錯管桁架結構，鑒于不同的桿件截面和結構尺寸，線性屈曲分析中易出現局部桁架的平面外屈曲，以及整體向上的豎向變形。

（2）采用“一致缺陷模態法”對大跨度交錯管桁架結構進行穩定性分析時，直接將線性屈曲分析所得第一階屈曲模態作為缺陷模式是不穩妥的，應分析不同屈曲模態的影響。

（3）在缺陷模式對大跨度交錯管桁架穩定分析中，個別屈曲模態對結構穩定性是有益的，而且局部失穩的屈曲模態以及多模態組合形式對結構穩定承載力的影響相對較小。

（4）對于大跨度交錯管桁架結構，在選擇線性屈曲分析所得屈曲模態作為缺陷模式時，宜避免采用局部失穩的屈曲模態，以及對結構整體穩定性有利的屈曲模態。對于缺陷幅值，應參考結構真實缺陷大小，對多種缺陷模式和幅值進行分別驗算來保證結構的穩定。