基于小波包分析的裝配式剪力墻套筒灌漿缺陷檢測

余毅斐周德源張晨昕張璇

（1.同濟大學防災減災工程系，上海 200092；2.福建省建筑設計研究院有限公司，福州 350001；3.山東科技大學建筑工程系，青島 266590）

0 引言

裝配式建筑是采用預制構件、部品部件在工地裝配而成的建筑。設計標準化、生產工廠化、施工裝配化、裝修一體化、管理信息化等是其基本特征。隨著技術發展，裝配式建筑以其高效率、高環保、低成本、構件質量好等優點逐漸符合現階段國情。其中裝配式剪力墻結構特別適用于住宅建筑，在工程實踐中得到了廣泛的應用。裝配式剪力墻結構是一種現代化的建筑結構形式，連接技術是預制裝配式結構的關鍵技術之一，也是保證其受力性能和抗震性能的關鍵。現有裝配式剪力墻的連接技術主要分為套筒灌漿連接、預留孔漿錨搭接、套筒約束漿錨搭接、機械連接等方法。在以上裝配式連接形式中，套筒灌漿連接具有更為廣泛的工程應用，是目前技術最為成熟的豎向鋼筋連接方法。

目前，已有學者對套筒連接裝配式剪力墻性能進行了大量研究，李向民等［1］對常用直徑的套筒進行灌漿缺陷預設，在套筒底部設置不同程度的缺陷并開展單向拉伸試驗，試驗表明，當缺陷長度小于30%的鋼筋錨固長度時，接頭單向拉伸強度尚能達到要求。鄭清林等［2］開展套筒灌漿缺陷種類和缺陷程度的多因素試驗分析，發現缺陷程度較大時，套筒連接接頭的承載力和變形性能均有較大程度下降。

綜上所述，套筒灌漿連接缺陷會直接影響連接接頭的各項力學性能，進而對裝配式結構整體的承載力、延性及抗震性能產生不利影響，故迫切需要建立套筒連接裝配式結構連接缺陷的檢測方法，而國內外相關的檢測方法研究較為有限。因此，本文對裝配式剪力墻開展了套筒灌漿缺陷檢測試驗，對試驗結果進行了詳細的記錄和分析，確定缺陷檢測參數，并通過有限元模型結果進行驗證比對，為裝配式剪力墻套筒灌漿連接缺陷檢測提供參考。

1 研究理論

小波包分析能同時對信號x（t）的低頻和高頻部分進行分解，將x（t）分解的頻帶任意精細化。在包含較多中高頻信息的信號中，這種分解能夠降低信號分解時出現的冗余和信息遺漏，時頻局部化分析效果好。缺陷的存在會使得結構動力響應變化，導致頻帶各成分產生不同程度的改變（增強或抑制），從而導致各頻帶信息重新分布［3］。因此，當結構局部存在缺陷時，其附近的動力響應所包含的信息，即各頻帶下的能量占比相對于完好結構會發生不同程度的改變。因此本文出于計算方便以及節省計算時間的目的，通過小波包分解，對這些頻帶上的能量進行統計，并提取能量特征參數，尋求缺陷參數在剪力墻各板帶中的分布規律。因而基于小波包能量譜在結構缺陷檢測上的研究運用孕育而生，并在鋼結構、橋梁結構等剛度較小的結構中得到了較多運用［4-5］。

信號基于小波包分解的總能量及各頻帶能量，可由式（1）—式（3）推導及得出。由小波包函數組｛ψj，k，i(t)｝構成的標準正交基中，各小波函數相互正交，由正交性可知，當m≠n時，則有

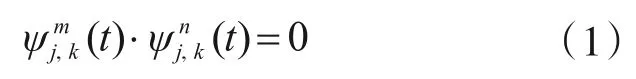
信號x(t)的總能量Ex為

由式（1）得：

式中：Eij表示信號經過j層小波包分解后，第i頻帶所攜帶的能量；Ex為信號的總能量，即各頻帶所帶能量之和。

2 試驗概況

2.1 試件設計

試驗采用裝配式混凝土剪力墻足尺試驗模型，包括頂梁、墻體和地梁三部分。模型立面圖和俯視圖如1所示，其中頂梁尺寸為1 980 mm×300 mm×300 mm，墻體尺寸為2 400 mm×1 580 mm×200 mm，地梁尺寸為2 580 mm×300 mm×500 mm，在墻體平面外方向前后各伸出800 mm。

模型混凝土強度均為C30，剪力墻內的連接縱筋、縱向分布筋、水平分布筋及箍筋均采用HRB400級鋼筋，參照彭媛媛［6］的全套筒裝配式剪力墻性能試驗，對墻體部分的連接與分布縱筋進行布置，套筒采用全套筒灌漿接頭，試件墻體配筋見圖2。

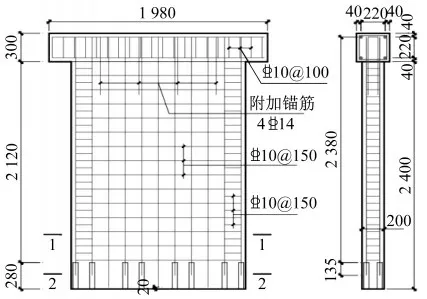
圖2 墻身及頂梁配筋圖（單位：mm）Fig.2 Reinforcement arrangement of wall and top beam（Unit：mm）

2.2 方案設計

共設計兩組試件進行試驗，其中，W1為對照組，即無缺陷試件，W2為存在套筒漏漿缺陷的試件。為引入不同程度的缺陷，參考韓笑等［7］的研究，將試件劃分為四個板帶，通過不灌漿的方式從左至右存在的缺陷套筒個數分別為3個、1個、2個和4個。采用直徑60 mm、孔徑5 mm、球重870 g的不銹鋼鉆孔擺球作為激勵源進行撞擊，擺球懸掛點與激振點垂直高度為500 mm。試件的每個板帶布置4個加速度傳感器，由坐漿層上表面開始，向上每隔300 mm布置一個測點，其中CD表示測點，第一板帶測點由下至上分別表示為CD1-1～CD1-4，第二板帶測點由下至上分別表示為CD2-1～CD2-4，同理可得測點CD3-1～CD3-4，CD4-1～CD4-4。板帶劃分、激振點及測點布置如圖3所示。

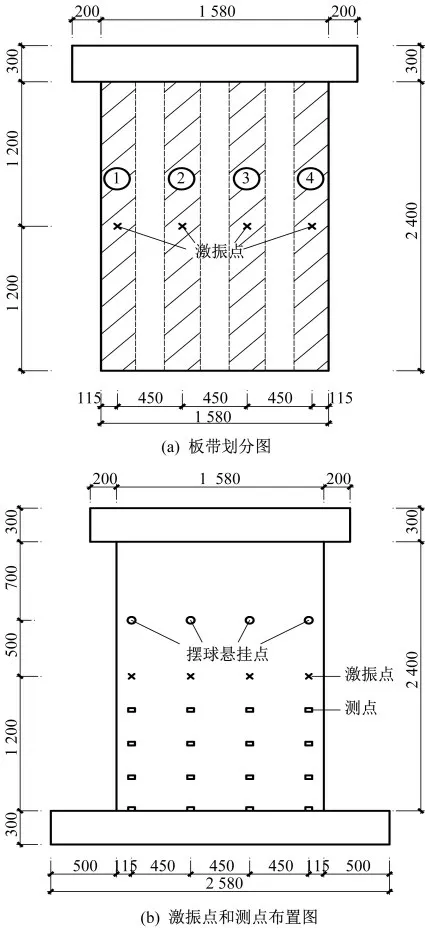
圖3 板帶劃分、激振點及測點布置（單位：mm）Fig.3 Strip division and excitation point layout（Unit：mm）

試驗激振方式和擺球下落高度見圖4，施加激勵時將擺球拉至預定高度處，由靜止釋放使其自由下落撞擊墻體形成激振。為避免擺球撞擊時產生的角度不同、受力不均等誤差，特在激振點處黏貼規格相同的墊塊，使試件所受激勵更為均勻合理，減小激勵誤差。

圖4 激振方式（單位：mm）Fig.4 Excitation method（Unit：mm）

2.3 試驗結果與分析

以W1和W2的板帶一為例，加速度時程響應曲線見圖5，其中加速度方向為垂直墻面。該曲線截取動力響應峰值前100 ms與峰值后900 ms的波形。可以發現對于同一試件、同一板帶不同高度測點的加速度曲線波形有很強的一致性，但加速度幅值各有不同，靠近坐漿層的測點加速度幅值最小，往上依次增大。

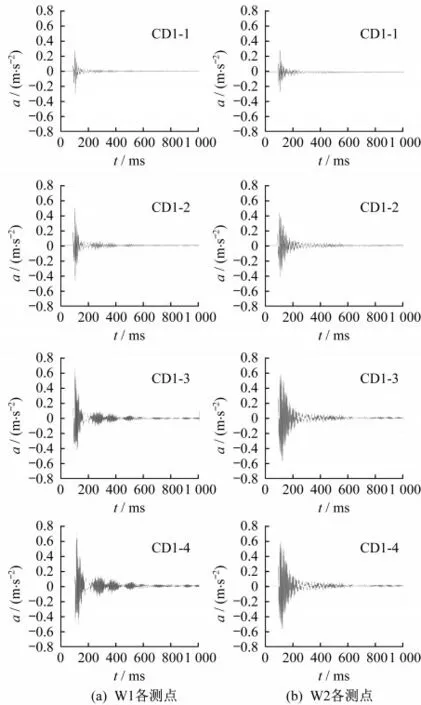
圖5 板帶一各測點加速度時程曲線Fig.5 Acceleration time history curve of each measuring point in strip 1

與試件W1相比，W2板帶一各測點的加速度時程響應有不同程度的變化。在完好試件W1中，板帶一的加速度時程響應曲線在衰減的同時，尾部伴隨著呈現出許多小鼓包，但這一波形特征在缺陷板帶卻并未出現。W2中板帶一的動力響應曲線較為飽滿，由初始達到峰值后平滑衰減。可以看出，相較于完好試件W1，試件W2各板帶加速度響應的變化程度與該板帶的缺陷程度存在正相關關系，缺陷程度越大的板帶，加速度時程響應的變化越明顯。

Zhang等［8］針對裝配式混凝土框架結構的套筒灌漿缺陷開展不同缺陷指標的識別對比研究，發現能量比偏差（Energy Relative Variation Deviation，ERVD）最為敏感，且在隨機性較大的錘擊激勵下仍表現出良好的穩定性。因此，本文決定采用能量比偏差（符號ERVD）作為缺陷特征參數。環境激勵不變時，相同結構的能量比變化理論上為0，結構缺陷后的能量比變化為一組數列，其均值大于0，并且在均值上下波動。定義ERVD來反映了能量比變化偏離均值的離散程度。

在第i板帶中，由坐漿層處的測點對CDi-1（i=1～4）計算所得的ERVD構成該板帶最下層的缺陷分量參數，命名為ERVD1；同理，坐漿層上部300 mm高處的測點，由CDi-2得到的缺陷分量參數為ERVD2；同理得到缺陷分量參數為ERVD3和ERVD4。

試件各板帶的ERVD數值見表1。其中，ERVDs=

表1 各板帶ERVD值Table 1 ERVD value of each strip

由表1可以看出，試件各板帶的ERVD數值大小與板帶的缺陷程度大小存在一定關系。

以試件不同高度的測點對為橫坐標，ERVD數值為縱坐標，用不同曲線代表不同板帶，繪制試件缺陷參數分布曲線，如圖6所示。可以看出，除了CDi-2以外，板帶四的ERVD數值均大于其余板帶，其次是板帶一，再次是板帶三，板帶二的ERVD值整體處于最低水平。這恰好與各板帶所含套筒連接缺陷的個數一一對應，套筒缺陷個數越多的板帶，所對應的ERVD數值越大，ERVD值與缺陷程度的大小呈正相關關系。

圖6 試件各測點ERVD數值分布Fig.6 ERVD value distribution of each measuring point of the specimen

以試件的不同板帶作為橫坐標，ERVD數值作為縱坐標，用不同曲線代表不同測點對所得出的結果，繪制試件缺陷參數分布曲線如圖7所示。可以看出，由下至上各測點的ERVD值逐漸減小，這是由于缺陷位于剪力墻底部套筒連接部位，距CDi-1最近，故最底端的測點對該缺陷更加敏感，當測點逐漸遠離套筒，其對應的ERVD值也逐漸減小。以ERVD值作為缺陷程度的判別標準，則CDi-1，CDi-3，CDi-4的識別效果較好，對缺陷程度的檢測結果均為板帶四＞板帶一＞板帶三＞板帶二，與實際情況相符，但CDi-2的識別效果較差。總體來說，各缺陷分量參數ERVDi對連接缺陷表現出了較好的敏感性，但為了避免試驗過程中難以消除的噪聲，激勵輸入偏差等誤差對結果產生的影響，取ERVDs作為缺陷參數更具有代表性。

圖7 試件各測點ERVD數值分布Fig.7 ERVD value distribution of each measuring point of the specimen

對各板帶的缺陷總參數ERVDs進行繪制，如圖8所示。可以看出，板帶缺陷越大其ERVDs也越大，ERVDs與其缺陷程度呈正相關關系。因此，ERVDs對裝配式剪力墻結構的缺陷具有很強的敏感性，可以作為良好的缺陷識別參數。

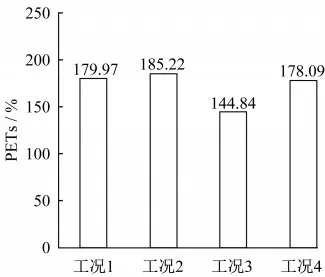
圖8 各板帶ERVDs數值分布Fig.8 ERVDs value distribution of each strip

3 結構分析模型

3.1 模型設計

采用有限元軟件ABAQUS建立裝配式剪力墻有限元模型，對試驗進行數值模擬。模型尺寸及配筋情況與試驗保持一致，下端采用固接約束，地梁與頂梁間采用彈簧約束。模型的激振點位于每個板帶的正中間，每個板帶布置四個測點，均位于激振點正下方，最低測點布置在坐漿層上部，往上依次間隔300 mm布置一個測點。普通混凝土及高強灌漿料均采用8節點六面體線性減縮積分單元（C3D8R），鋼筋采用三維一次桁架單元（T3D2）模擬，預制裝配柱內預埋的套筒采用8節點六面體線性減縮積分單元（C3D8R）來進行模擬。為了保證模型的缺陷情況與試驗保持一致，即第一板帶到第四板帶套筒的漏漿個數分別為3個、1個、2個和4個。當套筒發生整根漏灌時，將內部灌漿料的彈性模量予以折減（3 N/m2），該值與初始值相比（3.8×1010N/m2）可以忽略不計，以此來模擬試驗漏漿缺陷。整體模型、模型網格劃分、模型鋼筋骨架如圖11所示。

圖1 試件尺寸圖（單位：mm）Fig.1 Geometry of specimens（Unit：mm）

3.2 材料參數及激勵輸入

因本文的檢測方法為無損檢測，剪力墻在激勵下始終處于彈性階段，故模型參數不涉及塑性性能。混凝土結構模態阻尼比為0.05，其中鋼材材料密度取7 800 kg/m3，彈性模量為210 GPa，C30混凝土材料密度取2 400 kg/m3，彈性模量取30 GPa，模態阻尼比為0.05，FCD600套筒材料密度取7 300 kg/m3，彈性模量取154 GPa，灌漿料與座漿層材料密度取2 500 kg/m3，彈性模量取38 GPa。

圖9 有限元檢測模型信息Fig.9 Finite element model information

由于試驗條件限制，無法測得擺球錘擊墻體時的具體速度，因此無法得到荷載作用的具體時程曲線。由于小波包能量譜法對不同的荷載形式均具有很強的魯棒性，故可采用錘擊激勵對模型進行檢測。查閱文獻可知，瞬時沖擊激勵作用形式可以采用正弦半波曲線模擬，激勵曲線的作用時間為4 ms［9］，激勵峰值為1 kN，數據采集150 ms。模型中模擬輸入的瞬時錘擊激勵見圖10。

圖10 錘擊激勵輸入Fig.10 Excitation input

3.3 計算結果分析

施加錘擊激勵后，輸出每個測點z方向的加速度時程響應曲線，進行小波包分解和節點能量計算，提取所需檢測參數ERVD。各測點CDi-1～CDi-4的定義與2.2小節一致，由下至上各測點得到的缺陷參數分別為ERVD1～ERVD4。將各板帶的缺陷分量參數ERVD1～ERVD4與缺陷總參數ERVDs進行匯總后見表2。

表2 各板帶ERVD數值Table 2 ERVD value of each strip

圖11給出了各板帶的ERVD數值，以四條曲線表示四個板帶的ERVD，由上至下分別為板帶四、板帶一、板帶三、板帶二，表明在有限元計算得出的結果中，板帶四各測點的ERVD數值均處于最高水平，其次是板帶一，再次為板帶三，板帶二的各測點ERVD均為最低水平。這與板帶實際缺陷程度對應，可以看出套筒連接失效越多的板帶，其板帶內各測點ERVD數值也越大。

圖11 試件各板帶ERVD數值分布Fig.11 ERVD value distribution of each strip of the specimen

圖12給出了不同測點CDi-1～CDi-4的ERVD數值分布。與試驗一樣，距離缺陷較近的測點整體上ERVD數值也相對較大，表明距離越小對缺陷越敏感。CDi-1～CDi-4所得結果的識別效果均與實際情況相符，能夠準確識別缺陷大小。與試驗結果相比，有限元計算結果具有更好的識別效果，缺陷分量參數ERVD1～ERVD4對連接缺陷均表現出了較好的敏感性。

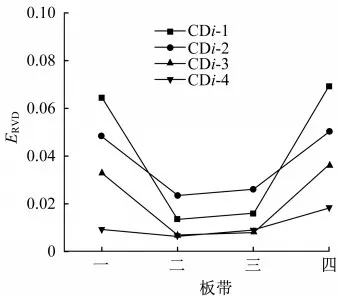
圖12 試件各測點ERVD數值分布Fig.12 ERVD value distribution of each measuring point of the specimen

為了避免驗中難以消除的噪聲及激勵輸入偏差等誤差的影響，取ERVDs作為板帶缺陷參數更具有代表性。將每個板帶的ERVDs值繪制成圖，結果如圖13所示。

圖13 各板帶ERVDs分布Fig.13 ERVDs distribution of each strip

可以看出，在數值模擬的結果中，缺陷總參數ERVDs與缺陷大小也存在著正相關關系，ERVDs的數值隨著板帶缺陷的增加而增加，即數值模擬檢測結果與試驗結果保持一致，如表3所示。

表3 基于ERVDs的板帶檢測結果Table 3 Strip test results based on ERVDs

由以上檢測結果可以分析得出，缺陷總參數ERVDs作為板帶的缺陷識別參數是具有說服力的，在其他條件相同時，無論試驗結果，還是數值模擬結果，ERVDs都與缺陷程度成正相關關系。

4 結論

本文對裝配式剪力墻開展了套筒灌漿缺陷檢測試驗，基于小波包能量譜，利用參數ERVD及ERVDs進行缺陷識別，并采用ABAQUS建立有限元模型，驗證了數值模擬開展套筒缺陷檢測研究的正確性。結論如下：

（1）在同一試件中，同一板帶不同高度的各測點，其加速度時程曲線具有很強的波形一致性，由下至上，測點加速度幅值依次增大。與試件W1相比，試件W2的加速度時程響應曲線，其波形和振幅均有不同程度的變化。

（2）缺陷總參數ERVDs與試件板帶套筒灌漿的缺陷程度呈正相關關系，板帶中套筒存在的缺陷數量越多，板帶的ERVDs越大。此外，對缺陷距離較近的測點ERVD值明顯更大，說明距離缺陷越近，傳感器能采集到的缺陷信息也越多，該缺陷參數的表征也越明顯。

（3）通過對比有限元模擬檢測結果與試驗檢測結果，可以看出試驗與模擬結論吻合，驗證了有限元模型的正確性。有限元模擬中，板帶不同測點的缺陷分量參數ERVDi與缺陷總參數ERVDs均有很好的檢測效果，考慮到實際操作可能存在的偶然誤差，選擇ERVDs作為最終缺陷檢測參數更具有容錯性和代表性。