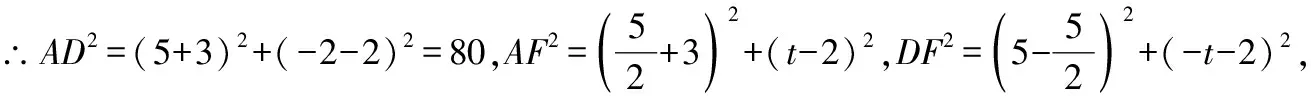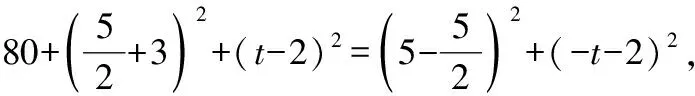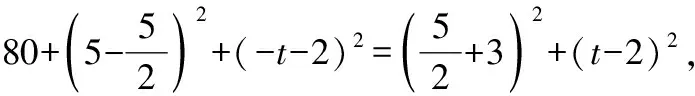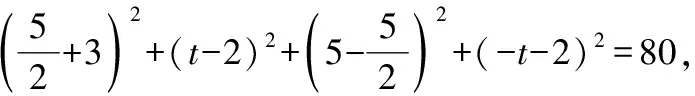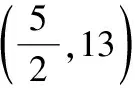漫談直角三角形存在性問題的解法

◎韓 強

(山東省東營市利津縣鳳凰實驗中學，山東 東營 257400)

2020年江蘇無錫中考題：二次函數=-3+3的圖像過點(6,0)，且與軸交于點，點在該拋物線的對稱軸上，若△是以為直角邊的直角三角形，則點的坐標為________

一、基本解法展示

基本解法1：=-3+3，當=0時，=3，

∴點坐標為(0，3)，

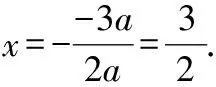
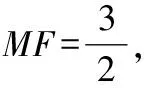
∵∠1+∠2=90°，∠2+∠3=90°，

∴∠1=∠3，又∠=∠=90°，

∴△∽△，

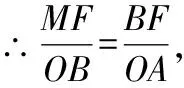
∴=6，

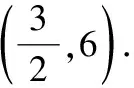
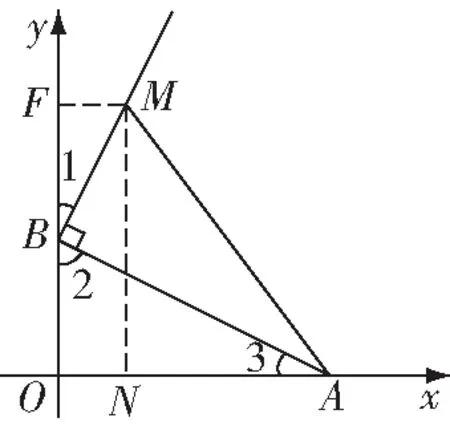
圖1

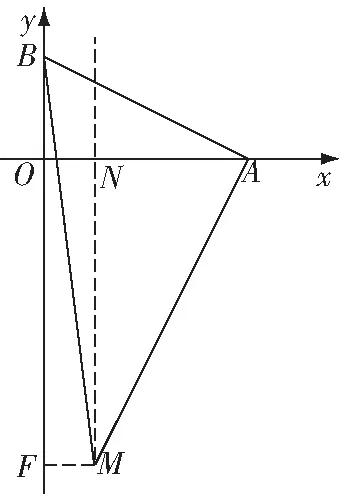
圖2

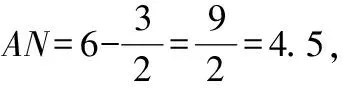
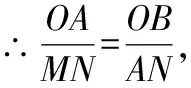
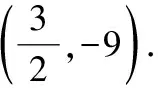
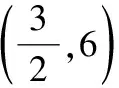
基本解法2：=-3+3，當=0時，=3，

∴點坐標為(0，3)，

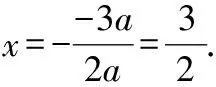
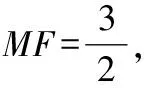
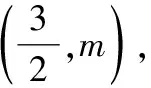
=+=6+3=45,

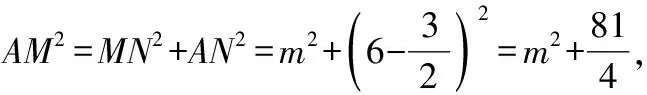
∵∠=90°，

∴=+，

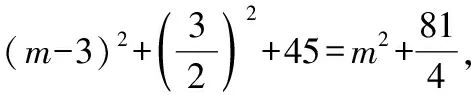
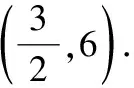
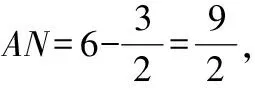
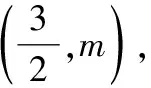
=+=6+3=45,

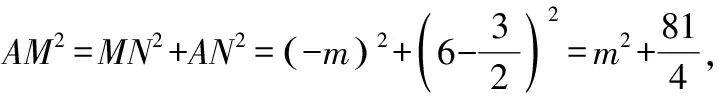
∵∠=90°，

∴=+，

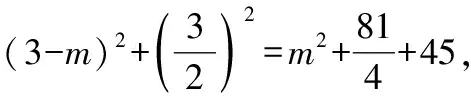
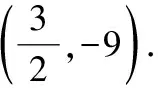
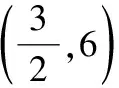
二、兩種基本解法的聯系與區別

基本解法1主要運用的是相似三角形的知識，基本解法2則主要運用的是勾股定理的知識兩種解法都是經典的巧妙解法，基本解法1創造性水平極高，是把“直角三角形存在”的條件進行了等價替換，使之轉化成了兩個直角三角形相似，然后運用分式方程求解，基本解法2是相對直接的思路，它直接運用勾股定理得到關系式，設定參數，并運用直角三角形中的勾股關系表達目標直角三角形的三邊平方，列整式方程求解解法1構圖精妙，解法2計算絕妙，根本區別還是思維的方向和運用知識點的不同解法1相對來說屬于“曲線救國”，適合思維能力較強的學生掌握，解法2則表現得比較直來直去，適合思維能力較弱的學生掌握教師在教學中兩種解法都應教給學生，但是應把解法2放在前面講授

其實，勾股定理何嘗不是由幾個相似直角三角形對應邊成比例的關系式推演得到的呢？射影定理中就包含了三個直角三角形循環相似的內容和勾股定理的結論這是直角三角形存在性問題能有兩種基本解法的根本原因直角三角形存在性問題的最主要的條件就是“直角的存在”，我們將“存在直角”的條件理解成兩個銳角互余的條件，就有了尋找兩個直角三角形相似的解法1，而將“存在直角”的條件理解成三邊所滿足的勾股關系的條件，就有了直接列出整式方程的解法2解法1還有“弦外之音”，值得深究和挖掘，而解法2就顯得“孤苦伶仃”了我們不妨把解法1叫作相似轉化法，把解法2稱為勾股定理法

三、相似轉化法的構圖策略

由解法1的構圖思路，我們將和相似無關的條件刪除，把二次函數的背景刪除，不難發現，基本的圖形有下面兩種，如圖3和圖4

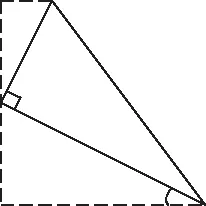
圖3

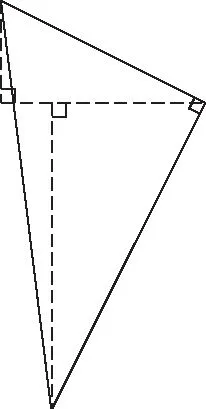
圖4

其實，構造相似的直角三角形就是解法1的基本策略我們只有構造出合適的圖形才能利用相似列出需要的比例式，并利用分式方程求出線段長下面的兩道中考題就是該題型與反比例函數和矩形結合的例子

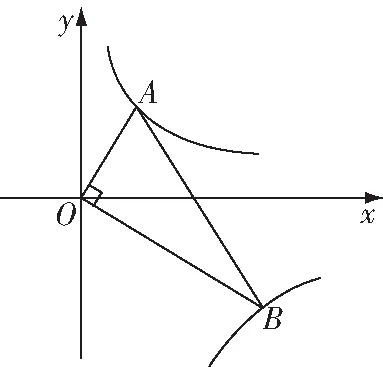
圖5

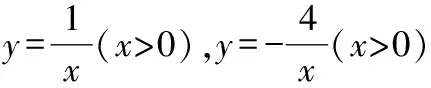
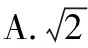
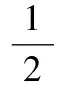
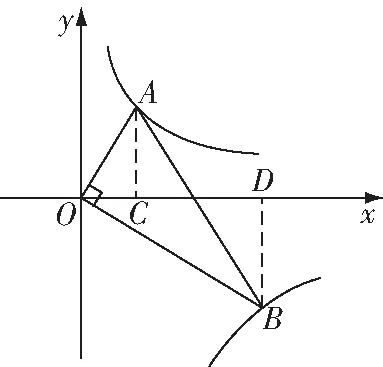
圖6

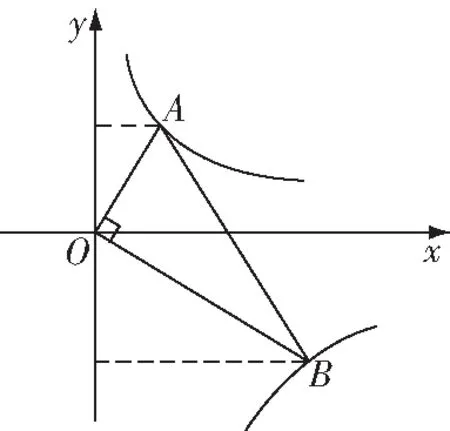
圖7

2020年山東煙臺中考題：如圖8，在矩形中，點在上，將矩形沿折疊，使點落在邊上的點處若=3，=5，則tan∠的值為( )

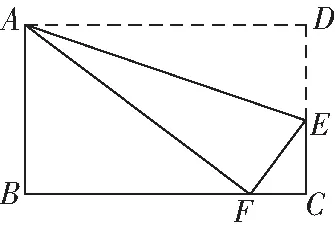
圖8

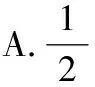
(勾股定理法)∵四邊形為矩形，

∴==5，==3，

∵矩形沿直線折疊，頂點恰好落在邊上的處，

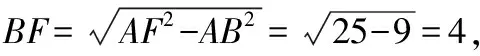
∴=-=5-4=1

設=，則==3-在Rt△中，

∵+=，

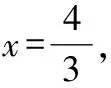
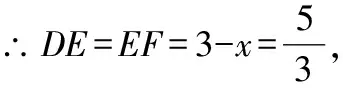
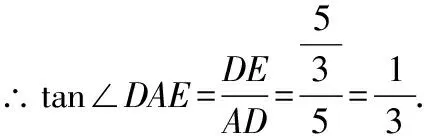
故選D.

試思考一下，用第一種基本解法——相似轉化法如何求解？

四、直角三角形存在性問題的特殊解法

這類問題中有的加了限定條件“以某條已知線段為直角邊”，這樣直角三角形存在的可能情況就減少了，不加此條件答案一般有四種

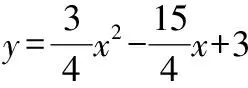
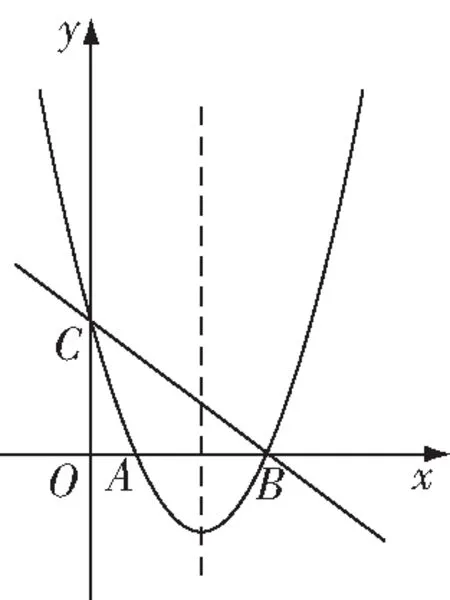
圖9

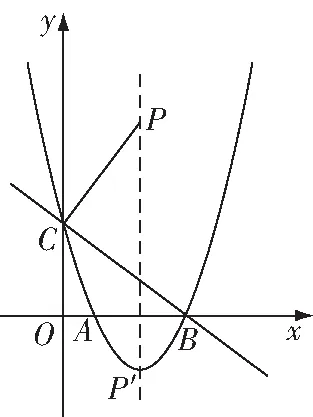
圖10

存在如圖10所示，

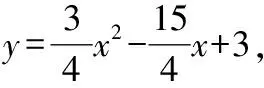
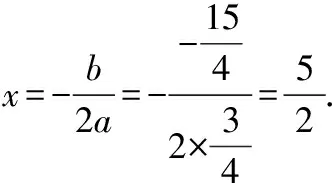
(1)當⊥時，△為直角三角形，

根據兩直線垂直時斜率的關系，

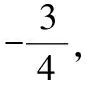
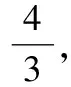
又∵直線經過點，

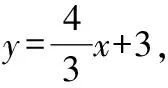
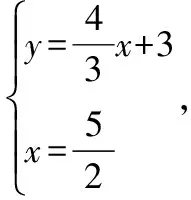
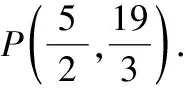
(2)當′⊥時，△′為直角三角形，

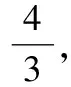
又∵直線經過點(4，0)，

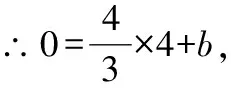
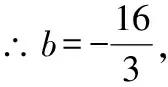
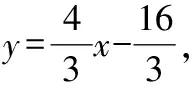
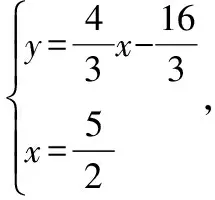
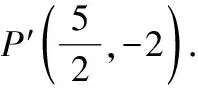
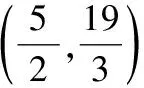
五、兩種基本解法的選擇方案

盡管兩種基本解法都是萬能的，但是不同題目的特點決定了我們選擇哪種方法一般情況下，如2020年江蘇省無錫市的中考題加了直角邊限定條件，構圖比較簡單，我們可以用相似轉化法，如果沒有這個條件，我們就直接用勾股定理法如下面的題目和解析，我們單純從得分和省時間的角度看，直接用勾股定理便于分類，且不必畫太多的圖下面的中考改編題有四個答案，我們如果用基本解法1，必須完成四個圖，非常煩瑣，若直接用勾股定理法，則后面的解析步驟整齊簡潔

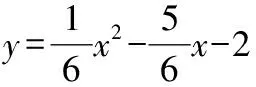
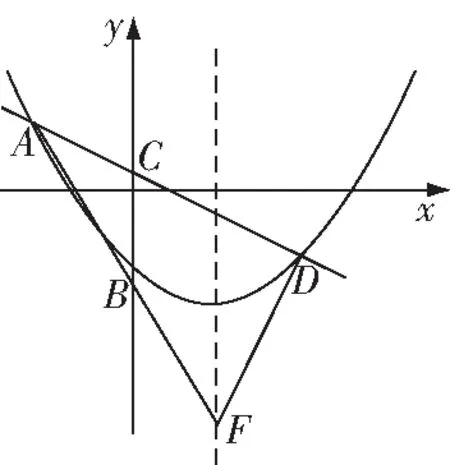
圖11

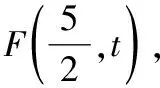
∵(-3，2)，(5，-2)，