HPM視角下的函數考源教學

◎李慧敏

(無錫衛生高等職業技術學校，江蘇 無錫 214000)

2016年12月7日至8日，全國高校思想政治工作會議在北京舉行習近平總書記強調，好的思想政治工作應該像鹽，但不能光吃鹽，最好的方式是將鹽溶解到各種食物中自然而然吸收

數學史是研究數學內部知識、外部事物發展需要及其規律的科學它不僅是一部從數學內在的原因來研究數學發展的歷史，也是一部從外在的社會原因來研究數學發展與其他社會因素間關系的歷史

筆者認為在課堂中教師應根據教學內容特點，挖掘教學內容中的育人要素，將其有機融入課堂教學中，潤物無聲，切實打通學科教育與思政教育緊密融合“最后一公里”在函數概念教學中，函數概念發展史猶如精神上的“鹽”，是學生深刻認識幾個階段函數概念的“調味品”適量放鹽，才能讓學生在咸淡適宜、味美可口的“課堂學習大餐”中汲取營養、受益終生

德國數學家克萊因曾將函數稱為數學的“靈魂”，并認為函數概念應該成為中學數學的“基石”函數是現代數學最基本的概念，是描述客觀世界中變量關系和規律的最為基本的數學語言和工具，在解決實際問題中發揮重要作用函數的概念是全部數學概念中最重要的概念之一縱觀300年來函數概念的發展，眾多數學家從解析式、變量說、對應說、集合的角度不斷賦予函數概念以新的思想，從而推動了整個數學的發展函數概念的一次次提出、一次次推翻、一次次修正、一次次完善，是后人對前人思維的一次次突破函數概念的演進過程可利用下表總結：

學說解析式說變量依賴說變量對應說集合對應說代表人物萊布尼茨和歐拉歐拉狄利克雷布爾巴基學派

在實際教學中，經常有學生會問:“在初中已學過函數，現在又要重新學習函數，那么是初中函數定義不對嗎？”為了回答好學生提出的問題，教師在教學過程中應該循著函數演變的進程，設計教學活動，讓學生了解函數發展歷程和函數概念演變的必要性，拓寬學生視野，使學生感悟數學的理性精神，提升學生的數學學科核心素養人們往往認為“歷史文化”與數學教學呈現“弱相關”，因為數學課堂中數學運算、邏輯推理和數據分析等主要數學活動似乎與人的生產生活、道德品質沒有直接的關聯事實上，數學教育中的數學歷史文化是深層次的，有其獨特的內涵

筆者近期就再現數學歷史、發展學生數學核心素養做了一些嘗試，下面結合這節課談談個人的認識和體會

一、教學實錄

(一)概念的引入

教師課前讓學生利用網絡資源，搜索整理函數概念的發展史，綜合學生的整理結果，基于學生的課前準備，提出問題，重現函數概念演變的歷史

設計意圖：在新課引入中，教師充分挖掘與數學教學內容相關的育人元素，滲透課程思政教育，也可以充分挖掘數學知識本身蘊含的教育因素與文化價值，如：數學文化、勵志榜樣、歷史人物、行業現狀以及數學發展動態與變革等素材

(二)概念的發展

案例1 某男童，5歲，因患急性支氣管炎，現按醫囑需用注射阿米卡星治療(按體重計算藥劑量)已知小兒用藥量按體重計算公式如下：

每次劑量=體重(kg)×每次每千克體重需藥量

注：阿米卡星小兒用藥為每次2 mg/kg；

5歲兒童正常體重范圍16 kg～20 kg

問題1 上述案例中，有幾個變量?變量之間的關系是如何體現的？

歷史材料 17世紀德國數學家萊布尼茨在手稿《反切線或函數方法》中用fuction一詞來表示某個特殊的幾何量，如一個圖形中的線段，正式文中幾個幾何量之間的關系導致“函數”演變成代數式1718年，數學家約翰·伯努利將函數定義為：一個變量的函數是該變量和一些常數以任意方式組成的量因此函數的定義拓廣到代數式1748年，歐拉在《無窮分析引論》中將函數定義為：函數是由一個變量和一些數或常量以任何方式組成的解析式

在當時的歷史條件下，數學家普遍認為函數就是解析式，但隨著新問題出現，如18世紀中期，數學家一直在爭論振動弦的問題：波動一根兩端固定的彈性弦，使其具有某種初始狀態，然后使其釋放振動你能用表達式表示變量間的關系嗎？

設計意圖：結合專業特征，設計教學案例教師從學生最近發展區出發，引導學生回顧函數解析式說，啟發學生思考：在現實生活中還有很多兩個相互依賴的變量是無法用表達式建立聯系的，該如何表示兩個變量關系？

案例2 波動一根兩端固定的彈性弦，使其具有某種初始狀態，然后使其釋放振動，彈性弦的振幅隨時間的變化情況如下圖所示

問題2 案例2中有變量嗎？如果有，有幾個變量？你能寫出變量之間的關系式嗎？

從這個例子中，我們發現，解析式并不能表示所有的函數關系，因此需要改進函數概念

歷史材料 由于“解析式說”并不能解釋所有的函數關系，歐拉在1755年《微分基礎》的前言中更新了函數的定義：如果某些量依賴于另一些量，當后面這些量發生變化時，前面這些變量也隨之變化，則前面的量稱為后面的量的函數至此，函數的“變量依賴說”取代了“解析式說”“解析式說”和“變量依賴說”兩種函數定義統治了相當長的歷史時期

設計意圖：教師遵循函數概念發展演變過程，啟發學生進一步思考，表述變量依賴關系的函數概念，培養學生勤于思考、嚴謹求實的學習品質

案例3 今年2月份全國新冠肺炎當日新增確診人數統計表如下

日期2223242526我國新冠肺炎當日新增確診人數10127610

問題3 上述表格中有變量嗎？如果有，有幾個變量？你能用變量依賴說解釋嗎？

歷史材料 1837年，德國數學家狄利克雷認為：如果對的每一個值，總有一個完全確定的值與之對應，那么是的函數“狄利克雷函數”的提出意義在于：這一全新的函數，突破了以往人們對于函數的印象，它既不能用統一的解析式表示，也不能用變量依賴說解釋狄利克雷定義的函數概念，第一次將函數定義域限定在一個區間上，打破了以往函數定義在整個實數集的局限這一定義就是人們常說的經典函數定義由此，函數的“變量對應說”取代了函數的“變量依賴說”

下面我們來回顧一下函數概念的三次演變

學說解析式說變量依賴說變量對應說代表人物萊布尼茨和歐拉歐拉狄利克雷

在上一章中，我們學習了集合，知道了用集合來表示對象既簡潔又清晰

問題4 你能說說這三個函數自變量和因變量的取值集合嗎？

(1)=2(16≤≤20)

(3)

日期2223242526我國新冠肺炎當日新增確診人數10127610

問題5 我們用集合表示了兩個變量的范圍，現在可不可以在變量對應說的函數定義下，重新在集合的視角下來定義函數呢？

歷史材料 20世紀康托爾創立了集合論，人們發現集合語言能簡潔清晰地表示一些數學對象，并且集合語言被稱為近現代數學的基本語言，廣泛地應用于數學各個分支學科因此，集合概念的出現使得函數概念得到了進一步的發展數學家龐加萊曾說過，有了集合論，數學的完全嚴格性就已經達到，用集合語言重新定義函數概念，是函數概念逐漸精確化的最佳途徑

設計意圖：在現實生活中，變量不僅可以代表實數，還可以代表不能表示大小的其他事物，既然變量都不是數字了，那么我們應該找一個更加寬泛的概念來描述這種關系，于是函數“集合對應說”應運而生

在這一環節中，教師通過三個案例和五個層層遞進的探究題，啟發學生遵循數學家探究生活中變量關系的思路，理順函數定義發展的脈絡，讓學生在獲取新知的同時，能感悟數學家治學嚴謹的態度

(三)概念的生成和理解

問題6=1是不是函數？如果是，定義域和值域分別是什么？

設計意圖：打破函數變量依賴說的慣性思維，教師引導學生從集合對應說角度，考察=1是否為函數，加深學生對函數集合對應說的理解

問題7 是否存在一個函數，使得非負實數對應1，負實數對應-1？如果可以找到，那么該函數定義域和值域分別是什么？

設計意圖：教師通過舉例構建函數，進一步加深學生對集合元素對應關系的認識

問題8 觀察圖像，是的函數嗎？說明理由

設計意圖：促進學生對定義中兩個變量的任意性和唯一性的理解，為辨別函數提供方法指導

問題9 下列函數是同一個函數嗎？

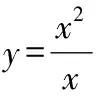
(3)=,∈{0,1}與=,∈{0,1}

設計意圖：教師通過同一函數的辨別，突出函數定義域和對應法則在函數概念中的地位，凸顯函數概念的本質

(四)課堂小結

教師引導學生回憶本節課的具體內容，從中梳理知識層面和精神層面的收獲，啟發學生思考函數概念演變歷史帶來的啟示：數學的研究方向很多，函數是一個基礎而深刻的概念，從邏輯上來說，內涵越小外延就越大如果一個概念定義越簡單，它能包括的事物就越多從函數概念的演變歷程可以看出，函數的定義需要眾多數學家的研究，更需要幾百年數學的發展作為基礎

二、學習反饋

課后問卷調查結果顯示：(1)在函數集合說概念理解上，課前有802%的學生認為=0不是函數，課中教師舉了一個類似的例子:=1是不是函數?通過函數集合說的概念學習，學生都認為這是一個函數，且能用集合對應關系來描述函數，并能指出定義域和值域(2)90%的學生明白了為什么初中學習過函數，現在要重新認識函數，并且明白現在所學的集合對應說的函數定義并非函數概念的最終形式，隨著問題層變化，可能還會出現新的函數概念，研究更加復雜的函數關系(3)在課后測驗中，我們發現大部分學生想了解數學概念發展的歷史，喜歡聽數學家構建數學知識的故事，愿意遵循數學家的足跡認識和重構新知識同時大部分學生希望“在數學課中穿插數學家的故事和言行”因為他們認為對比以前課堂上背概念、背公式和刷題，現在這種學習方式更有趣、更生動，他們不僅能感受到數學家的治學嚴謹，還能感受數學家背后折射出的人性光芒，既拓寬了他們的知識面，又使他們感受到數學課程滲透的人文精神

三、教學反思

通過學習，學生追隨數學家們的腳步，經歷函數概念從“解析式說”到“變量依賴說”，再到“變量對應說”，最后到“集合對應說”的整個發展過程，獲得了對函數概念的深刻理解，同時積累了數學探究的經驗，感受到數學的演進性特征整節課中，學生遵循數學家探究現實生活中變量關系的路徑，在問題情境探究中，共同揭示現實生活中各種變化過程背后的客觀規律，不僅了解了數學概念的發展史，還在舊知的基礎上構建了新知，建立更加穩固的函數概念知識網絡圖

通過“函數”一課的教學實踐，筆者認為，在課堂上再現數學歷史，發展核心素養，不能僅僅停留在“貼標簽”層面，教師要結合具體的教學內容，從教學目標的確定、教學過程的實施到教學評價，都要有核心素養培育的意識，充分挖掘教學內容中核心素養培養的素材，找準切入點，關注生長點，慢慢滲透，長期培育，逐步提升學生的數學核心素養

(一)再現歷史，重構知識

數學知識具有厚重的歷史文化背景，數學的發展史就是數學知識的演變史本課采用的史料主要是通過歷史文獻得出結論：早期數學家在函數概念的理解上存在困惑，源于紛繁復雜的世界，歷史是一面鏡子，歷史相似性的存在告訴我們，如果我們能走進另一個時代、另一種文化的數學家的心靈中，那么我們就能更從容地走進同一個時代、同一種文化的學生心靈中，一起循著數學家的足跡，重新構建知識

(二)改進方式，理解深刻

本文采用歷史發生教學原理，結合護理專業特點，整合教學資源，呈現知識自然發生全過程荷蘭著名數學教育家弗賴登塔爾認為數學學習主要是進行“再創造”，教師只有讓學生經歷了知識的“再創造”過程，才能將知識以它最初被發現時的樣子表現出來，才能將數學冰冷的美麗轉變成火熱的思考因此本節課通過再現歷史、改進教學的方式，將知識發生過程進行濃縮，側重于主題發生發展的關鍵步驟、概念發生及發展中的思考過程，讓學生深刻理解知識的發展呈螺旋式上升在一定的歷史背景下，人們將某個概念定義為一種形態，隨著紛繁復雜的事物變化以及人們探尋解決問題的認知力的提升，某個概念的呈現也會發生變化數學教學不能割裂數學歷史，了解歷史，有助于我們更好地理解和教授數學概念這種呈現方式既符合函數概念發展的歷史脈絡，又符合函數概念發展的邏輯脈絡課堂中學生回憶已有的函數知識時，大多數學生對函數的理解還是局限在一次函數、反比例函數和二次函數的層面，也就是函數概念發展的第一個階段解析說因此，教師應從解析式定義出發過渡到另外三種定義，站在學生認知的起點，構建學生的認知脈絡

(三)精神引領，素養培育

源于教材、高于教材的內容蘊含著數學思想方法、理性思維、情感態度、問題解決的能力等，需要教師從素養培養的視角進行適當的加工和挖掘學生通過數學學習，養成善于思考、以理服人的行為習慣，形成重論據、有條理、合乎邏輯的思維品質，感悟嚴謹求實的科學精神和一絲不茍、精益求精的工匠精神本節課中數學學家研究概念的思維方式，刨根究底、嚴謹治學的科學精神等隱性的教育素材，是數學教育提升學生學科素養、實現立德樹人目標的有力支撐