循環小數與實數構造理論

◎王斌儒

(甘肅有色冶金職業技術學院建筑與信息工程系，甘肅 金昌 737100)

一、引 言

數學是研究現實世界的數量關系和空間形式的科學追本溯源，數學最初的工作是計數在計數過程中，人類首先接觸到自然數，自然數系由于實際生活和數學運算需要用到它，而逐漸擴充到整數系，再擴充到有理數系

有理數系是一個比較完美的數系：它具有稠密性，即任何兩個有理數之間必含有有理數；它對四則運算是封閉的，即任何有理數經加減乘除四則運算后仍然是有理數；它的元素有順序關系，因而可以比較大小，進行不等式運算有理數系的這些性質使得古希臘人認為它就是所有數的全體，并且設想把它們由小到大、連續無空隙地排列在一條無限長的直線上，即在全體有理數與直線上全體點之間建立一一對應關系，這種和諧自然的連續性設想促使古希臘數學家畢達哥拉斯提出萬物皆數的名言但事實并非如此，公元前500年左右，畢達哥拉斯學派的希帕索斯發現正五邊形對角線長是不可公度的，繼而發現正方形的對角線長是不可公度的，即單位邊長的正五邊形和正方形的對角線長不是有理數希帕索斯的發現動搖了古希臘幾何理論的基礎，同時，第一次展示了有理數系的缺陷：有理數盡管鱗次櫛比地排在數軸上，但并沒有布滿整個數軸，數軸上面還存在不能用有理數填補的空隙然而希臘人并沒有建立起無理數的一般概念

孕育于希臘時代的微積分思想與方法，經過了漫長時期的醞釀十七世紀下半葉，牛頓和萊布尼茨創立微積分到了18世紀，微積分在應用領域取得了巨大的成功但是，隨著數學本身的發展以及人們對物理領域中微觀現象的深入探討，微積分學初創時期粗糙的邏輯表述，已無法令人滿意，形成了方法上有效但邏輯上無法自圓其說的矛盾局面

微積分學邏輯基礎上的嚴重問題，雖然暴露了出來，但是并沒有能夠及早地得到解決這就促使十九世紀的許多數學家，回過頭去重新分析邏輯基礎，即分析理論的嚴格化

微積分是建立在極限運算基礎上的變量數學，而極限運算需要完備的實數域最終，構建完備實數域的任務在19世紀下半葉被完成，微積分學也進入了新的發展階段

二、實數系的建立

我們從自然數系出發，可以構造出有理數域，這是一個對四則運算封閉的、稠密的有序域如果我們進一步從變量數學的角度來考察問題的話，則它還存在本質上的缺陷從分析學的基本運算——極限的角度來考慮，有理數域在極限運算下，不是一個封閉的數域，正像自然數集在減法或除法運算下，是不封閉的一樣某些有理數序列本身盡管有凝聚的趨勢，但是在有理數的范圍內卻找不到極限值，有理數域的這種“不完備性”，正是它本質的缺陷當我們把數從有理數集擴充到實數集后，便解決了這個矛盾

(一)實數的定義

我們采用十進數，來定義實數

設∈，∈{0,1,…，9}(∈)，?，只要>，就有<9

我們稱…為十進數，即實數的十進表示，簡稱實數，實數集記為實數集中循環小數表示的實數叫作有理數，不循環小數表示的實數叫作無理數

下面本文借助十進數和標準列來說明循環小數是如何表示有理數的

(二)標準列與循環小數

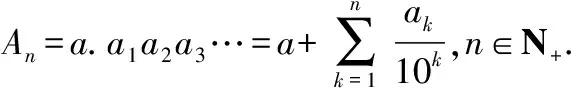
事實上，我們定義了可稱為標準列的有理數列為一個實數

標準列是柯西列

下面我們給出循環小數的定義

對第二類循環小數的標準列我們可進行類似討論

由此可見，兩類循環小數的標準列收斂到有理數，稱循環小數為其標準列極限的十進表示

不同的標準列不等價

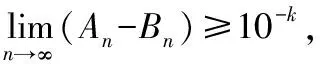
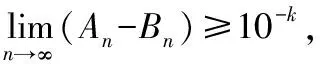
不同的循環小數表示不同的有理數

由引理1即可證明

有理數都可以表示成循環小數，即有理數是循環小數對等的標準列的極限

只需證明每個正的真分數都可以表示成循環小數

上述過程中，一旦出現余數為0，除法運算就終止，這時得到有限小數；在相反的情形中，即余數不為0，則余數列無限，因為0<<，所以余數列中至少有兩項相等存在最小的下標及正整數，使得=+，并且(當>1)時+1，…，+-1兩兩不等，且不等于由的定義，可知，…，-1兩兩不等，都不等于

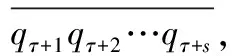
綜上可得，任何一個有理數存在唯一一個循環小數為其表示，每個循環小數都表示一個有理數循環小數表示的有理數是這個循環小數標準列的極限

三、實數的基本關系

實數的基本關系是圍繞柯西列展開的

(一)實數的運算規律

任意一個有理數的柯西列，存在唯一一個標準列與其等價

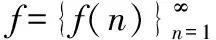
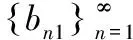
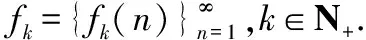
當0…不以9為循環節時，是標準列

當0…以9為循環節時，有兩種情況

①對?∈,=9，規定數列()=+1，∈

②∈,使得<9,當>時恒有=9此時，規定

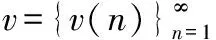
因為不相同的標準列不等價，所以與一個柯西列等價的標準列唯一

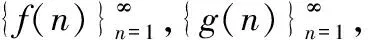
由極限的運算法即可證明

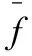
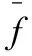
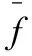
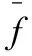
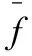
由此可見，實數的運算本質上是標準列之間的運算

(二)實數的序

任取實數=…，其中∈若≥0，且所有的不全為零，則稱為正數，記作>0；若所有的全為零，則稱為零，記作=0；若<0，則稱為負數，記作<0若實數,滿足->0，則稱大于，記作>，或者小于，記作<記不大于為“≤”； 記不小于為“≥”

(三)實數的絕對值與三角不等式

實數的絕對值

我們稱||為實數的絕對值，顯然||≥0

設>0，則||

若>0，則>-顯然成立，||<即<

若≤0，則<顯然成立，||<，即-<，兩邊加上-即得-<

三角不等式

①||=|-| ②|·|=||·||

③|+|≤||+|| ④|||-|||≤|-|

(四)實數的稠密性

兩個有理數之間必然存在一個有理數，同樣任意兩個實數之間總有一個有理數或無理數，即實數連續地布滿了實軸

有理數的稠密性

設,是兩個不同實數，且<,則存在有理數，<<

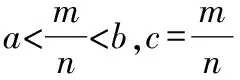
無理數的稠密性

設,是兩個不同實數，且<,則存在無理數，<<

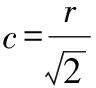
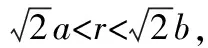
(五)實數的完備性

有理數經過擴張得到的實數，關于加、減、乘、除運算仍是封閉的，事實上實數關于極限運算也是封閉的下面我們來給實數列的收斂下定義

實數列的收斂

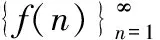
設數列的通項公式為()=…，∈

實數系的完備性

從有理數系擴充到實數系后，在實數范圍內，柯西列均收斂，稱為實數的完備性完備性是實數連續地布滿實軸的反映

滿足0≤()-()≤10-，從而有理數列與等價

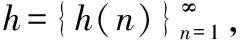
由此可見，任何有理實數的柯西序列在實數域內都有極限

四、歷史上的實數構造理論

實數，看起來很淺顯，幾乎人人都知道它，也會用它進行四則運算，但數學家偏偏要問：“究竟什么是實數？它有什么性質？”從古希臘開始，這個問題困惑了數學界2000多年

實數系的邏輯結構問題被19世紀下半葉的數學家所正視，人們在確認有理數系的建立工作已完成的基礎上，無理數被認為是主要的難點最終戴德金和康托等人以不同方式完成了完備實數域的構造

(一)Cantor的實數構造

Cantor首先定義了基本序列

給定有理數序列{}，若?>0，?自然數，當,>時，有|-|<，則稱{}為基本序列

考慮全體有理數基本列{}所組成的集合，在上引進一個等價關系，如下:

關系“～”是一個等價關系，即滿足：

①自反性 {}～{}

②對稱性 {}～{}，則{}～{}

③傳遞性 若{}～{}，{}～{}，則{}～{}

等價關系～把分成若干個等價類不同等價類里的有理數基本列是互不等價的，而在每一個等價類里，都可以任選一個有理數基本列作為代表，它完全確定了該等價類

有理數基本列的集合按等價關系“～”劃分的每一個等價類稱為一個實數

康托把每一基本序列定義為一個實數兩個這樣的序列{}與{}是同一個實數當且僅當|-|在趨向于無窮時趨向于零

我們用，，…來表示實數，實數集記作每個等價類中的任一數列{}都稱為該實數的一個代表，即有理數基本列{}是實數的代表當且僅當{}∈

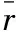
如果基本列{}在有理數范圍內不存在極限，我們就稱以它為代表的等價類所確定的實數為無理實數從而，實數由有理實數和無理實數構成

(二)Dedekind的實數構造

Dedekind借助幾何直觀，在直線的啟發下來定義無理數他觀察到當直線上的點劃分成兩類，使每一類中的點都位于另一類中的點的左邊時，就必然有一點且只有一點能夠確定此分劃，所以直線上的任何一點與它確定的劃分是一回事，正是這一特性使直線成為連續不斷的于是，為了建立實數的連續性，Dedekind用集合的觀點分析了直線(實數域)連續性的本質，把有理數全體分為兩類(用大小代替左右次序)，由此來唯一地界定實數

若將全體有理數劃分為非空的兩類：與，中的每一個數都小于中的任一個數，則稱此為有理數的一個分劃，記為(|)如果中有一個最大數，或中有一個最小數，那么稱此分劃為有理分劃(此時存在一個有理數，即中最大者或中最小者，它確定了此分劃)；如果中沒有最大數，或中沒有最小數，那么稱此分劃為無理分劃，并稱(|)為無理數

全體有理數再加上如上引進的全體無理數稱為實數系，記作我們對這一系統再進行分劃，就與上述對有理數系所做的分劃不同了若將全體實數劃分為非空的兩類：與，中的每一個數都小于中的任一個數，則稱此為實數系的一個分劃，記為(|)

Dedekind證明了Dedekind連續定理，即對實數系的任一分劃(|)，或中有最大數，或中有最小數，兩者必居且僅居其一

該定理說明，任何一個實數分劃都可以由一個實數來產生，大于該數的實數為一類，小于該數的實數為一類，至于該數，則屬于兩類之一這樣類似于直線上點的分割，實數也成為一個連續的系統，簡稱為實數連續統