基于Drude-Lorentz模型的金銀納米顆粒光譜特征研究

朱圣清，楊 芳

（1.江蘇理工學院 化學化工學院，江蘇 常州 213001；2.江蘇理工學院 機械工程學院，江蘇 常州 213001）

太陽能是人類取之不盡、用之不竭的清潔可再生能源，具有成為世界主流能源的潛力。與降低太陽能電池制造成本相比，提高其光電轉換效率是提升競爭力的必經之路。為了提高光伏器件的光電轉化效率，人們提出了多種增效技術手段[1-5]。其中，利用貴金屬納米顆粒如金銀的局域表面等離激元（Localized Surface Plasmon，LSP）效應提升光伏器件性能，已成為近十年來的研究熱點[5-7]。

局域表面等離激元是貴金屬納米材料所具有的一種特殊光學現象，其本質為金屬表面區域的自由電子與激勵電磁波相互作用形成的一種電磁模式[8]。這類現象一般發生在粗糙的金屬與介質界面或離散金屬納米顆粒表面，其能量傳遞方式主要有散射和吸收。當激勵光源頻率與金屬材料本征頻率接近或相等時，這種散射和吸收作用最大，即為局域表面等離激元共振（Localized Surface Plasmon Resonance，LSPR）。這種局域化的表面等離激元應用于光伏器件時，作用類似于納米天線[9]，把入射光場的能量強烈局域在納米顆粒周圍，產生強烈散射作用。這種作用可以把垂直入射于光伏器件的太陽光轉化為大角度入射光并多次反射，增加了入射光與光伏材料間的有效作用長度，從而提高了對入射光能量的吸收率。表面等離激元效應的強弱與貴金屬納米材料的尺寸、形狀和結構等形貌特征息息相關。人們利用不同微觀形貌的納米顆粒增強了光伏器件的光電性能，在吸收率、量子效率及光電轉換效率方面都有了顯著的提升。

應用于光伏器件的納米顆粒形態多樣，有棒狀、三角板狀、半球形、星形等[10]。相對于非球體納米顆粒，球體或類球體納米顆粒制備簡單、成本低，因而具有推廣優勢。Chen等人[11]用核狀銀納米顆粒增強非晶硅太陽能電場，使其電池短路電流提升了14.3%。Xia課題組[12]研究了球形納米顆粒在異質結有機/硅光伏器件上的作用機理，認為表面等離激元的局域場增強作用是提高光伏器件光電轉化效率的主要原因。從能量轉化的角度考慮，納米顆粒對入射光產生消光作用可分為兩個部分：一是通過散射作用入射光轉化為大角度的散射光，并在光伏器件中多次反射，使其更好地被光伏器件吸收后轉化為光電流，形成電能，成為入射光在太陽能電池中的有效利用部分；二是部分能量被金屬納米顆粒自行吸收，轉化為熱能，在光伏材料及納米材料上耗散掉，造成能量的損失。迄今，對球形貴金屬納米顆粒在光伏器件性能上的研究較多，但關于納米顆粒的尺寸及其對入射光的自吸收與散射比例關系的研究仍較少。

本文基于Drude-Lorentz模型，利用最小二乘法得到了優化的金銀材料折射率函數表達式；結合Mie理論，研究了金銀球形納米顆粒的消光光譜、吸收光譜、散射光譜等特性；比較并分析了不同尺寸下金銀納米光譜特性的差異。研究結果可為納米材料的光譜分析，以及納米材料在光學中的應用提供理論依據。

1 理論模型與計算方法

1.1 球形金屬納米顆粒散射、吸收、消光系數的表達

對于顆粒尺寸d與入射波長λ滿足d/λ<0.1時，Mie理論是求解其光學特性的有效方法。此時，整個顆粒范圍內的電磁場相位可看作一常數，計算顆粒周圍的場分布時，可以將入射光當作靜電場來處理[13]。圖1為金屬納米顆粒Mie理論模型示意圖，球體半徑為a，球心位于坐標原點，均勻且各向同性的金屬球處在靜電場中，金屬的介電常數為ε(ω)，ω為入射光圓頻率，周圍介質介電常數為εm。根據麥克斯韋電磁場理論可求得金屬球外圍空間的電勢為：

圖1 金屬納米顆粒Mie理論模型示意圖

發生共振時，金屬納米球周圍電場得到了極大增強，入射光與金屬納米顆粒發生相互作用，在顆粒表面發生吸收與散射作用。由坡印亭矢量計算得出的金屬納米顆粒的散射截面Csca、吸收截面Cabs與消光截面Cext分別為：

其中：k為入射光波矢，k=2π/λ；Cext=Csca+Cabs，散射截面Csca正比于a6，吸收截面Cabs正比于a3。給定金屬納米顆粒半徑a，環境介質介電常數εm，以及金屬介電常數ε，即可求得納米顆粒散射、吸收及消光截面[14]。隨著金屬納米顆粒尺寸的增大，散射效應越來越顯著。當發生共振時，金屬納米顆粒對入射光的散射和吸收作用同時得到增強。

1.2 金銀介電常數的擬合

金屬納米球體的散射、吸收及消光系數的計算精度，與介電常數εm和波長λ密切相關。在小于或近紅外波段，金屬材料的折射率可以用Drude-Lorentz模型描述[15]：

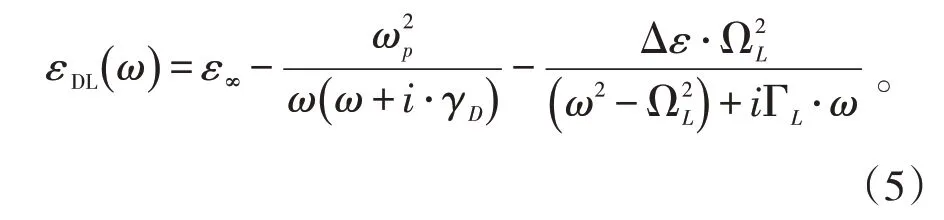
其中，ε∞、ΩL、ΓL、Δε、等離子頻率ωp、弛豫系數γD均為待定常數。根據公式（5），結合金銀材料的實測折射率參數[16]可得到公式常數。為了優化擬合結果，采用最小二乘法，所得擬合方程為：

其中：ωj為實測數據對應離散波長的圓頻率，即為離散波長對應的介電常數實測數據；εDL(ωj)為以ε∞、ωp、γD為自變量的Drude-Lorentz模型擬合函數。

1.3 介電常數的解析表達式

當Φ取最小值時，利用matlab運算公式（6），即可得到ε∞、ωp、γD、ΩL、ΓL、Δε等常量的值，見表1。

表1 基于Drude-Lorentz模型的Au、Ag介電常數擬合值

根據表1參數，可得到Drude-Lorentz模型下金銀介電常數的函數表達式。考慮到ω=2πc/λ，金 銀 介 電 常 數 的 函 數 表 達 式分別為：

圖2為公式（7）得到的介電常數實部、虛部與文獻[15]實測數據的對比圖。可以看出，基于Drude-Lorentz模 型 的 解 析 表 達 式εAu()λ，在500～1 000 nm范圍內，與實測數據吻合得很好。實部幾乎重合，虛部在長波長區域只存在較小的偏差，相對誤差在10%以內；在金表面等離激元共振敏感波段（520 nm左右），相對誤差為5.88%；在1 000 nm處兩者偏差為7.1%。500～1 000 nm覆蓋了大多數金納米顆粒表面等離激元效應的共振波長，因此通過Drude-Lorentz模型利用表達式εAu()λ可以有效地計算金納米顆粒的光譜特性。

圖2 金的介電常數擬合值與實測數據對比

同樣，為了比較銀的介電常數與光學手冊中數據的相符程度，利用公式～n=n+i?k、εreal=n2-k2、εimage=2nk，得到材料銀的折射率實部與虛部，見圖3。可以看出，εAg()λ的擬合值在波長300～1 000 nm范圍，兼顧了折射率實部與虛部的準確性，兩者數據誤差較小，可較真實地反映銀材料的光電特性。

圖3 銀的折射率擬合值與實測數據對比

綜上，通過Drude-Lorentz模型的擬合，得到金銀材料介電常數與波長的函數關系，為金銀納米球Mie理論的求解提供了便利。

2 納米球體的光學特性

2.1 金納米球的吸收、散射、消光截面

圖4為理想金納米球體在不同粒徑時的吸收、散射和消光截面。由圖4可見：金納米球體吸收、散射和消光截面大小與納米材料粒徑相關，粒徑越大，吸收、散射和消光截面越大；在半徑為50 nm時，吸收、散射和消光截面分別可達4.48×104nm2、2.25×104nm2、6.67×104nm2，球體幾何最大截面πr2為0.785 4×104nm2，消光截面為球體幾何最大截面的8.5倍。同宏觀材料消光截面與幾何截面幾乎重合的特性相比，納米顆粒可產生多倍于自身幾何截面的消光效果，因而具有顯著的強散射作用。圖4表明，理想球型金納米顆粒的局域表面等離激元共振峰在529 nm處，這一結果與已有實驗結果[17]幾乎相同。這也表明，對于類球型納米材料，納米顆粒光學特性采用Mie理論處理，可以與實驗結論較好地匹配。從擬合結果還可看出，不同半徑納米顆粒的表面等離激元共振峰位置與半徑大小依賴關系不明顯。這是由于在納米顆粒半徑較小的情況下，Mie理論處理納米顆粒為極化的偶極子，這種偶極子電場極值的計算與體積無關，在外界光場激勵下產生受迫振蕩，所以在理想模型下，金納米球體的表面等離子共振頻率不是體積函數。

圖4 不同半徑理想金納米球體的光學特性

當納米顆粒應用于光伏器件時，往往期望其能增強對入射光的散射，減小顆粒自身的熱效應，通過提高對入射光的整體吸收率，進而增強太陽能電池的光電流，因此，就需要定量分析消光現象中吸收和散射作用所占的比例。

圖5展示了不同半徑大小金納米球的散射消光比（Csca/Cext），結果表明：散射消光比與納米顆粒粒徑相關，較小的納米粒徑消光中吸收作用占據了較大比例，而隨著粒徑的增大，散射作用隨之加強；入射波長為529 nm即共振時，半徑為10 nm、20 nm、30 nm、40 nm、50 nm理想金納米球體的散射消光比依次為0.76%、5.65%、12.81%、19.36%和37.13%。可見，消光比的值是波長的函數，在表面等離激元共振位置，該比值相對較小。與圖4對比還可以發現，Csca/Cext極小值與納米顆粒表面等離激元共振波長位置并不重合，Csca/Cext極小值在494 nm處，與Csca或Cext極值529 nm存在35 nm的波長差。這是由于金納米材料在紫外波段具有額外吸收作用，使得消光極大值左右分布不對稱造 成的。

圖5 不同半徑理想金納米球體的散射消光比

2.2 銀納米球體的吸收、散射、消光截面

與金納米球體吸收、散射、消光特性的研究過程相同，本文同樣計算了半徑r為10 nm、20 nm、30 nm、40 nm、50 nm理想銀納米球體的表面等離激元共振特性，如圖6所示。圖6（a）比較了不同半徑銀納米顆粒的吸收截面Cabs。吸收截面為半徑的函數，顆粒尺寸越大吸收作用越強。對于r=50 nm情形，最大吸收截面可達2.28×106nm2。同時，模擬結果表明，對于銀納米顆粒，表面等離激元共振峰位置在415 nm處，這一結果與Wiley等人采用DDA算法計算銀納米球的結論相吻合[18]。圖6（b）展示了不同銀納米顆粒的散射截面Csca，可以看出其散射作用相對金而言更強；半徑為10 nm、20 nm、30 nm、40 nm、50 nm的銀納米球，散射截面峰值分別為4.06×104nm2、2.59×105nm2、2.96×106nm2、16.62×106nm2和63.38×106nm2；對于r=50 nm的銀納米顆粒，散射截面為幾何截面的2 116倍，這表明銀納米顆粒對入射光有極大的散射效應。根據吸收截面和散射截面，進一步計算了消光截面Cext及散射消光比Csca/Cext。圖6（c）和6（d）比較了不同半徑銀納米顆粒的消光截面及散射消光比。與金納米顆粒的光譜特征相似，銀納米顆粒的消光截面為粒徑和波長的函數，即顆粒尺寸越大消光作用越明顯，在表面等離激元共振波段，消光作用最強。相比金納米材料，銀納米材料對入射光的消光作用更顯著；且在消光現象中，散射作用的貢獻更大。如當入射波長為共振波長415 nm時，半徑為10 nm、20 nm、30 nm、40 nm、50 nm理想銀納米球體的散射消光比依次為17.85%、63.46%、85.44%、93.29%和96.45%。從圖6（d）還可看出：除最小顆粒r=10 nm外，其他尺寸納米材料的散射消光比在整個波段均可達60%以上；顆粒半徑50 nm、入射光波長大于300 nm時，散射消光比可達95%以上。這表明，相同尺寸的銀納米球比金納米球的散射效應更強，可以使更多的入射光轉化為大角度散射光，從而提高光伏器件的太陽能吸收率。

圖6 不同半徑理想銀納米球體的光學特性

3 結論

運用Drude-Lorentz模型，根據金銀實測介電常數擬合了金銀介電常數函數表達式。根據Drude-Lorentz模型擬合的折射率表達式，利用Mie理論計算了不同半徑金銀納米球的光譜特性；得到半徑為50 nm的銀納米球體，在415 nm共振波長條件下，散射消光比可達96.45%；相比金納米球在529 nm共振波長下37.13%的散射消光比，銀納米顆粒的散射消光作用更強，能夠大幅提高光伏器件的太陽能吸收率。