零極點特性在數字濾波器基礎實驗教學中的應用
肖 涵,李苑青
(哈爾濱工業大學〔深圳〕 實驗與創新實踐教育中心,廣東 深圳 518055)
一、課程實驗簡介
“數字信號處理”課程是通信工程、電子科學、信息工程等專業的核心課程,具有知識點多、理論性強、應用性強特點,廣泛應用在工程實踐及科學研究中。數字濾波器設計是“數字信號處理”課程的一個重要內容,是圖像處理、模式識別等后續課程的基礎,國內外高校一般會在理論教學的同時,配置相應的實驗內容,以加強學生對數字濾波器的理解與學以致用的能力。
數字濾波器的性能與濾波器的零極點分布密切相關,濾波器頻響特性曲線的形態是所有極點和零點共同作用的結果。系統的極點分布多用于判斷系統的因果性和穩定性,因果穩定的數字濾波器所有極點在單位圓內。系統的零點分布影響濾波器的相頻特性,例如,因果穩定系統的所有零點都在單位圓內則為“最小相位系統”。在實際應用中,零極點分布圖除可以用于判斷系統因果性與穩定性外,與系統的其他性能(濾波器類型、通頻帶位置等)之間同樣聯系緊密。對于零極點的計算,若系統函數的分母、分子多項式階數較高,手工計算極點與零點比較麻煩,可采用MATLAB中的求根函數roots來計算。在“數字信號處理”的實驗部分,對于已知系統函數的數字濾波器,分析零極點分布主要用到MATLAB中的zplane函數。我校針對信號處理類實驗,配備了虛擬儀器平臺,通過在平臺上直接輸入數字濾波器系統函數分子分母的系數,可以直接得到零極點分布圖。本文圍繞零極點分布與濾波器類型、通頻帶特性,結合虛擬儀器平臺與軟件仿真,探討零極點特性在數字濾波器基礎實驗中的應用。
二、極點與零點在濾波器實驗的應用
根據濾波器結構是否存在反饋,數字濾波器可以分為FIR濾波器和IIR濾波器。FIR濾波器為非遞歸型濾波器,具有嚴格的線性相頻特性且由于其單位脈沖響應為有限長度的,FIR濾波器為穩定的系統。IIR濾波器結構中存在反饋回路,其對于輸入信號的響應是無限延續的,IIR濾波器可能是不穩定的。
(一)濾波器零點分布與阻帶中心頻率
N階FIR濾波器的系統函數為:
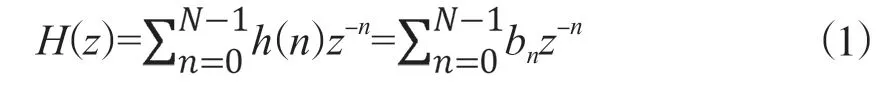
FIR濾波器的極點在圓心處,在MATLAB仿真中利用zplane(B,1)來繪制FIR濾波器的零點分布,其中B為表示b的數值序列。圖1為軟件計算及虛擬儀器平臺得到的3階FIR濾波器零點分布,右圖中顯示了零點的極坐標及零點-圓心連線長度、與實軸正向夾角。
為了得到FIR濾波器的頻率響應特性,一種方式是在MATLAB中直接計算,另一種方式是在虛擬儀器平臺上搭建濾波器,將離散時間信號輸入至濾波器來得到濾波器的頻率特性。圖2是學生在實驗中實現的FIR濾波器,通過掃頻法或逐點法得到濾波器的幅頻響應。函數發生器產生模擬信號輸入至采樣保持器,采樣時鐘由數字輸出模塊提供,在一個采樣脈沖時刻對模擬信號采樣,信號幅度在下一個采樣脈沖前處于穩定狀態,采樣保持器輸出的離散時間信號進入濾波器。通過掃頻或逐點測量,可以得到圖1系數下濾波器的阻帶中心頻率。
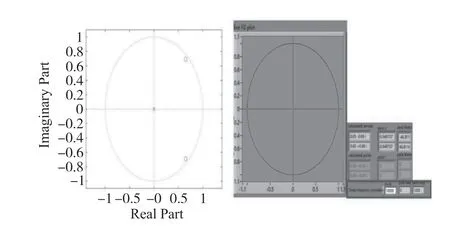
圖1 軟件(左)與虛擬儀器平臺(右)計算零點分布(b0=1,b1=-1.3,b2=0.902)

圖2 虛擬儀器平臺搭建的3階FIR濾波器
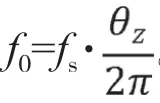
(二)濾波器零點分布與濾波器類型
N階IIR濾波器的系統函數為:
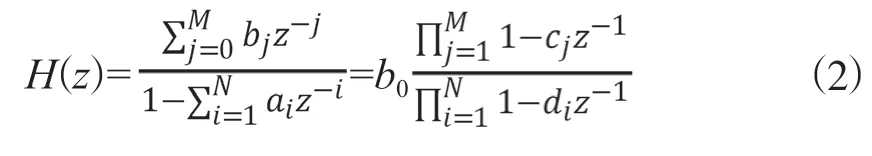
其中在c和d分別為濾波器的零點與極點。采用幾何方法研究IIR濾波器零點與極點分布對頻率特性的影響,系統函數在單位圓內的極點處出現峰值、且極點越靠近單位圓,幅度特性的峰值越高越尖銳;系統函數在零點處出現谷值,且零點越靠近單位圓,谷值越接近零。因此,可以根據z平面上零點與極點的位置,對給定頻率范圍內濾波器的類型進行快速判斷。
在數字濾波器基礎實驗的預習部分,學生通過IIR濾波器系統函數的分子多項式系數初步判斷濾波器的類型,圖3是實驗中虛擬儀器平臺計算的三種3階濾波器的零極點分布圖(綠色x為極點,紅色○為零點)。三種濾波器的2階極點均位于單位圓內,即濾波器系統穩定。其中(1)所示對應的濾波器的2階零點位于z平面實軸-1位置處,由此判斷(0,2)范圍內濾波器類型為低通;(2)中濾波器的2階零點位于z平面實軸1位置處,因此可以判斷(0,2)范圍內濾波器類型為高通;(3)中濾波器有兩個1階零點,分別位于z平面實軸-1位置與1位置處,由此判斷濾波器在(0,2)范圍內為高通濾波器。此外,若給出對模擬信號采樣的頻率,可估計濾波器的幅頻響應。
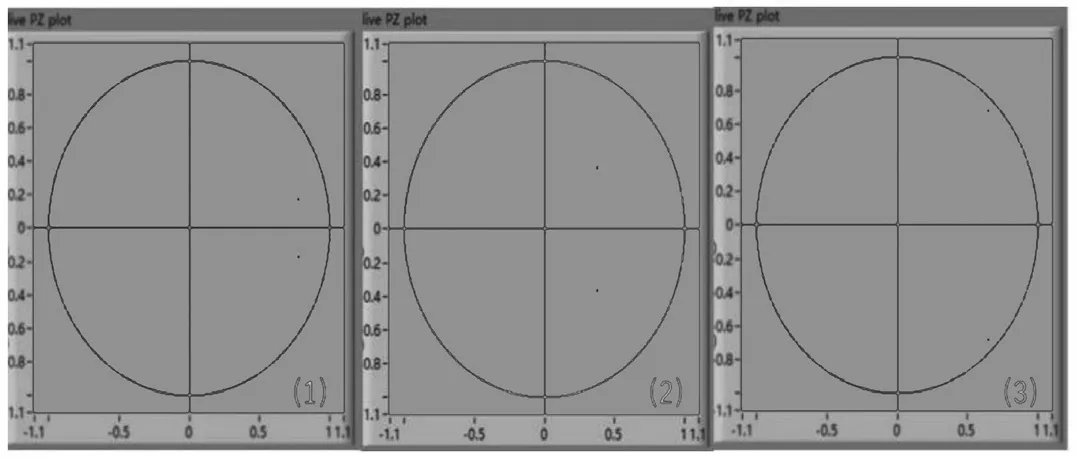
圖3 三種濾波器z平面的零極點圖
(三)濾波器極點位置與峰值頻率

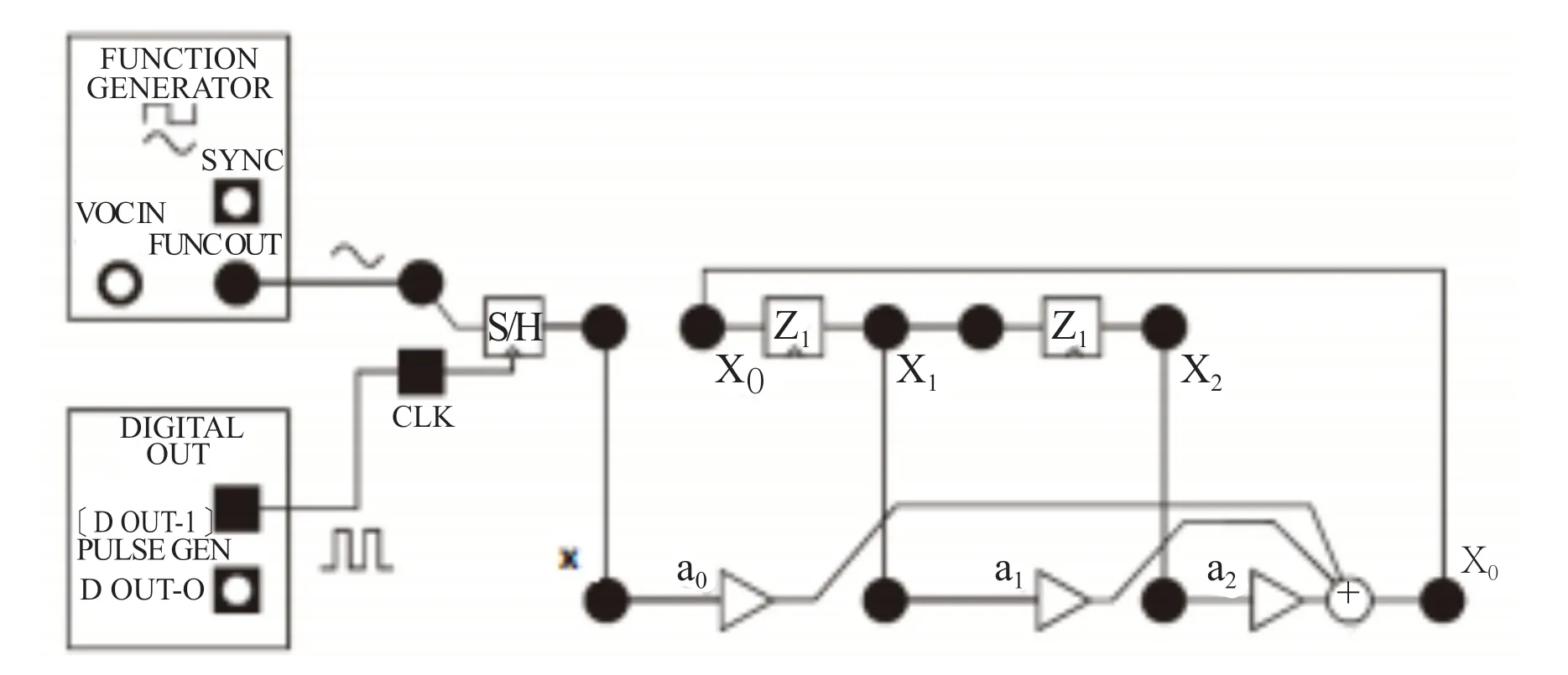
圖4 虛擬儀器平臺搭建的3階IIR濾波器
三、采樣頻率與濾波器的特性
在實踐應用中,對模擬信號進行數字處理的過程可能會涉及采樣頻率的改變,采樣頻率改變后濾波器的通阻帶位置將發生偏移。為了在改變采樣頻率后保持數字濾波器的通頻帶位置不變,一種方式是重新設計濾波器,而另一種方式則是通過改變極點位置得到新的濾波器參數。數字濾波器的中心頻率和阻帶截止頻率可通過軟件仿真計算準確得到,而基于虛擬儀器平臺搭建數字濾波器則有助于學生理解濾波器設計與實現過程中的實際問題。虛擬儀器平臺搭建的數字濾波器,模擬信號經過采樣保持器離散化后輸入濾波器。若加倍采樣頻率,濾波器的中心頻率將改變,理論上將極點相位調整為原相位的一半,可保持濾波器的中心頻率不變。在實驗過程中,利用虛擬儀器平臺可求出零極點位置,但濾波器的中心頻率可能需要微調才能達到設計參數指標。
需引起學生注意的是,如果只改變極點位置而系統函數分子多項式系數不變,由于采樣信號的頻譜與采樣頻率成正比關系,采樣頻率提高后濾波器幅頻響應的峰值幅度將增大,考慮到虛擬儀器平臺硬件條件的限制,在實驗中信號可能由于內部節點飽和而造成濾波器輸出信號信噪比降低,因此,在采樣頻率發生變化后除需關注輸出端的幅頻響應,還需關注濾波器的中間節點。綜上,在設計數字濾波器時極點與單位圓的距離要適當,如果距離單位圓過近,濾波器系統具有非常高的增益,容易導致濾波器節點的信號發生飽和;而零點位于單位圓上,可使濾波器的幅頻響應在阻帶具有最大的衰減。
結語
本文從零極點特性出發,在數字濾波器基礎實驗中利用虛擬儀器平臺及仿真軟件繪制了零極點在z平面上的分布,分析了零極點分布對濾波器類型、通頻帶特性的影響,并探索了模擬信號離散化過程中采樣頻率對濾波器通頻帶位置及增益的影響。教學實踐表明,通過本文所述實驗內容,有助于學生對零極點特性與數字濾波器的設計形成直觀的認識,進而強化學生對知識點的理解與應用。

