前伸后延構體系 上下貫通促思維
——以人教版數學教材五年級下冊“分數的基本性質”為例

車淑麗

（朝陽市喀左縣第四小學）

“分數的基本性質”一課是“數與符號的認識”單元主題中的內容，是在學生已經掌握了商不變的規律、小數的性質、分數的意義以及分數與除法的關系的基礎上進行教學的。從商不變的規律到小數的性質再到分數的基本性質，這些規律都是在“變與不變”中凸顯本質特征、感悟數學思想的。因此，作為一節生長課，本節課我力求從學生已有的知識經驗引入，通過數學思維方法的再現和遷移，將學生帶到“最近發展區”，為學生鋪設一條思維路徑。在探究過程中，我引導學生運用數形結合的方法歸納概括分數的基本性質，并且借助圖形揭示分數相等的秘密，引導學生理解規律背后的本質特征。學生經歷猜想、實踐、觀察、驗證的全過程，在“變與不變”中探究、發現規律，初步感知“等價類”以及“無限”的數學思想，培養了數感，發展了數學推理意識。這樣，能夠為學生后續學習約分、通分提供依據，為“分數的計算”及“比的基本性質”的學習打下堅實的基礎。

一、從點出發，激活學習經驗

小學數學知識是一條線。“前伸”就是弄清楚知識（包括數學概念、原理、方法、規則、思想、思維等）的源頭和發展脈絡，解決“從哪里來”的問題；“后延”就是要弄清楚知識的發展趨勢，解決“到哪兒去”的問題，兩者是統一的。只要從這樣的視角來備課、上課，數學課就會變得有意思、有意義。

（一）憶舊導新，鋪設思維路徑

江蘇省特級教師許衛兵認為，數學是一門“關系”學。如果我們從“關系”的視角來研究教材內容和教學方法，就會使知識系統化，使教學結構化，從而使學生的思維走向“自能”化。“分數的基本性質”一課就是在舊知的基礎上延伸生長而來的。學生在學習小數的性質和商不變規律的時候已經在不經意間應用到了“于變中把握不變”這一思想方法，積累了相關的思維經驗。因此，本節課可從商不變的規律和小數的性質入手，讓學生認識到“研究數學現象的變化特點，從變中把握不變，是發現規律的重要方法和途徑”，為本節課的學習奠定堅實的方法基礎。

教師可提出問題：（1）8÷4→80÷40；（2）24÷6→12÷3。觀察這兩組算式，你發現了什么？

生：我發現每組算式中被除數和除數都變了，但是商卻沒變。

生：第一組算式中被除數和除數同時乘以10，第二組算式中被除數和除數同時除以2。

生：我想到了商不變的規律——被除數和除數同時乘以或除以一個相同的數（0除外），商不變。

師：商不變的規律就是我們從“變與不變”的大量除法算式研究中歸納發現的。等式0.1=（ ）你會填嗎？看看什么變了？怎樣變的？什么沒變？

生：0.1=0.10=0.100=0.1000=0.10000……可以寫出無數個。

生：雖然小數末尾0的個數逐個增多，但小數的大小是不變的。

生：我想到的是小數的性質——小數的末尾添上0或去掉0，小數的大小不變。

師：小數的性質也是從大量“變與不變”的例子中研究發現的。看來，研究數學現象的變化特點，從變中把握不變，是發現規律的一個重要方法和途徑。（板書，變、怎么變、不變）

（二）溝通聯系，引發合理猜想

教師通過新舊知識之間的聯系，引發學生合理猜想，學生能自然地將學習內容納入其已有的認知結構體系。

師：整數除法中有商不變的規律，小數中有小數的性質。那么，請同學們結合本單元學習的內容，猜想一下，分數中有可能存在什么規律？你的依據是什么？同桌之間互相說一說。

生：我認為分數中也存在著一定規律。根據分數與除法的關系，我們可以把“被除數”看作“分子”，把“除數”看作“分母”，把“商”看作“分數值”，所以我認為分數中存在的規律與商不變的規律是基本相同的。

生：我認為分數中存在著一定的規律，而且這個規律也一定是在“變與不變”中發現的。

師：同學們，你們抓住了知識之間的聯系進行猜想，還想到了運用“變與不變”這一思維方法來研究，真了不起！老師為你們點贊！（板書，猜想）

二、自主探究，理解規律本質

（一）比較大小，形象感知相等

美國心理學家布魯納曾經說過：“數學的生命在于探索，教師的任務是讓學生親歷探索的過程，在探索中發現，在探索中創新。”因此，本環節教師設計了不同層次的探究內容，通過對分數大小的比較，借助直觀圖形，引出一組相等分數，讓學生初步感知相等的內涵。

師：根據分數與除法的關系來比較分數的大小和借助圖形來說理，都是好方法。同學們請看圖（如圖1）。

圖1

（二）實踐操作，嘗試尋找相等

教師要提供豐富的學習材料，引導學生動手實踐，用畫一畫、折一折、擺一擺、說一說等方法找相等的分數，使學生初步感受其中的“變與不變”，從而對變化規律有淺顯的、感性的認識。同時，教師還可引導學生聯系生活找相等的分數，或者利用分數與除法的關系找相等的分數，這樣能擴大相等分數的研究范圍。

自學提示：請打開學具袋（相同的圓形、正方形、長方形紙片各4張，10根小棒，線段圖，彩筆），用畫一畫、折一折、算一算、寫一寫等方法，嘗試找出“分子、分母不同，但大小相等”的分數。（至少找出兩個）你也可以聯系生活實際，找一找生活中相等的分數。把你找到的分數寫在練習本上，與小組內同學交流，說明為什么相等。

師：通過實踐操作，相信你們一定找出了很多相等的分數，誰來說一說？

生：我把圓形（或正方形）的紙片對折，涂上其中的1份，就是；然后，我再對折，涂色部分就占圓形的；再對折，涂色部分就占圓形的涂色部分沒變，所以分數的大小相等，也就是

考古學文化是隨著考古學研究發展到一定時期和水平出現的概念。德國考古學家古斯塔夫·科西納是第一個運用考古學文化來整理考古材料的人，他認為，從舊石器時代晚期以來，中歐的考古記錄就可以用文化和文化群來安排。他提出“文化群即民族群，文化區即民族區”，因此文化的差異就反映了民族的差異。科西納聲稱，在地圖上標出的一類器物的分布代表了某一民族的分布，而文化的延續反應了民族的延續，于是，考古學能夠根據器物確定的文化單位來追溯民族群體的分布和延續。但科西納是一個典型的種族主義者，他試圖通過考古學文化的整理尋找德意志民族的起源。

師：如果再對折一次，涂色部分就占圓形的幾分之幾？它們的大小還相等嗎？

生：我想我會得到無數個相等的分數，因為涂色部分始終沒變，所以分數的大小也不變。

（三）借圖揭秘，凸顯相等本質

教師要抓住學生匯報中對折的方法，借助圖形直觀演示，揭示性質背后的本質特征，即不同分數之間為什么相等，滲透“等價類”的數學思想。教師通過讓學生想象“如果一直對折下去，你會找到多少相等的分數？”滲透“無限”的數學思想，這也為下面怎樣“變”才會“不變”以及規律的概括提供了有力的支撐。教師課件演示。（如圖2）

圖2

師：確實，如果我們無限地對折下去，可以得到無數個相等的分數。借助直觀圖形，我們來觀察一下，這個圖形究竟發生了什么變化？

生：我發現無論怎么分，只不過是涂色部分和整體分的份數變多了，但涂色部分的大小是不變的。

生：從圖中我們可以看到，將圓形平均分成2份時，涂色部分是1份，當將圓形平均分成4份時，涂色部分就隨之變成了2份，當將圓形平均分成8份時，涂色部分就隨之變成了4份，分得份數變多了，也就是分子和分母同時變大了，但變化前后他們所表示涂色部分的大小是相等的。

生：因為我們平均分的是整個圓，所以分子和分母是同時分的，份數多了，每一份變小了，但所表示涂色部分的大小是不變的。

師：其實，無論是哪一個分數，只要它所對應圖形中的每一份發生了相同的變化，所得到分數的大小就是相等的。

三、整體建構，形成知識體系

學習的過程也是學生認知基礎與新知相互協同、整體建構的過程。課堂上，教師要將新知化歸舊知，在溝通聯系中滲透“類比”的數學思想方法；要利用舊知解釋新知，進一步實現知識的遷移和內化，形成知識體系。

師：同學們，你能根據分數與除法的關系以及除法中商不變的性質來說明分數的基本性質嗎？

師：我們利用以前學習的商不變的規律推理、解釋了分數的基本性質。實際上，商不變的規律與分數的基本性質是可以相互轉化的，等我們到了六年級還會認識比的基本性質，到那時你們就會更加深刻地體會到數學知識之間的內在聯系，真是“數學很奇妙，關系最重要”。

四、內化延伸，探尋本質特征

本課練習不能只停留在對知識和技能的掌握上，教師還要引導學生通過練習獲得一定的感悟、聯想和提升。

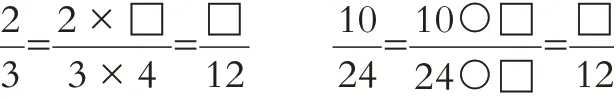
學生回答“是根據分數的基本性質找到的”之后，教師可引導學生通過討論交流，形成如下的理解：

通過“找朋友”的游戲，讓學生找相等的分數，加深了學生對分數基本性質的理解和運用。

最后，教師可設置“寫數”題：A、B點分別表示哪些數？你能寫出多少個？

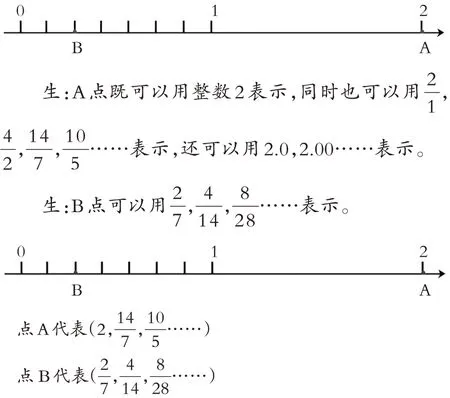
師：分別觀察A點和B點所寫出的數，你有什么發現？

生：我發現A點用分數或小數表示，都可以寫出無數個，用整數表示只有一個；而B點不能用整數或小數表示，只能用分數表示，也有無數個。

師：同學們真是善于觀察和總結！確實，數軸上所有的點（0除外）都可以用無限個分數表示，盡管這些分數不同，但是它們表示的是同一個點，所以大小是相等的。我們還發現，數軸上的點，有的能用整數表示，而且只有一個。有的點卻不能用整數表示，由此也就產生了分數。

本題將分數和整數的重要區別直觀地呈現在學生面前，學生進一步感悟到分數不同于整數的重要特性之一就在于“等價性”，感受“無限”的數學思想，進一步加深理解了分數產生的意義。