PSO-LS：一種非視距環境下目標定位方法*

金超 汪 洋

（1.武漢郵電科學研究院 武漢 430070）（2.南京烽火天地通信科技有限公司 南京 210019）

1 引言

近些年的研究中定位問題的測量和距離估算技術已初步成熟。定位測量模型主要分為距離測量技術和角度測量技術（Angle of Arrival，AOA）等。在基于測距的定位模型中非視距（Non-Line Of Sight，NLOS）誤差是影響定位精度的關鍵因素，而非視距誤差由于其統計特性不穩定，常常給定位精度帶來較大影響。

如果目標和所有信標節點之間信號進行視線傳播（Line Of Sight，LOS），則可以獲得較高的定位精度。然而，在從目標到信標的直接路徑被障礙物阻擋的情況下，信號測量行進中的過量路徑導致的測量誤差使得定位精度受到影響，該誤差被稱為NLOS誤差。

非視距誤差目前主要研究方向有非視距傳播的識別、非視距傳播誤差的抑制、非視距傳播的利用及非視距場景下的定位方法設計四個方面［1～2］。本文主要的研究方向為非視距場景下的定位方法設計。

在NLOS 環境下進行定位，有NLOS 判別、魯棒求解定位位置、利用啟發式算法定位求解等幾種方案。針對NLOS 和LOS 混雜環境，文獻［3］提出使用到達時間差（Time Of Arrival，TOA）和AOA 結合的NLOS 識別方法，文獻［4］通過Anderson-Darling檢驗進行NLOS判別，從而區分LOS和NLOS。

魯棒求解定位位置無需知道任何距離模型的參數，也不需要任何關于NLOS 測量的統計屬性先驗信息。文獻［5］針對線性最小二乘方案中隱含無誤差測量假設問題以及其半定松弛（Semidefinite relaxation，SDR）解的不穩定性，提出使用平方距離測量的方案，通過將原定位問題轉換為廣義信任域子問題（Generalized trust domain subproblem，GTRS）進行求解。文獻［6］在此基礎上進一步證明了該方案對NLOS 誤差抑制的有效性，該文使用距離倒數加權的方式對測量距離進行加權處理，從而達到抑制NLOS 誤差的效果。文獻［7］使用二等分法求解GTRS，提升了模型定位的精度。文獻［8～10］分別從兩步加權最小二乘、基于中位值的最小二乘、使用模糊加權的最小二乘等方面對NLOS 定位誤差進行限制。然而，基于魯棒最小二乘方法的定位計算往往需要通過多個測量點的多組測量位置來提高測距精度且其計算量相對較大。

同時使用啟發式算法求解目標位置的方法得到了部分學者的重視。文獻［11］通過遺傳算法使用一組測距信息對目標位置進行快速計算，但由于只使用單次信息，對于非視距環境的定位效果不佳。針對于該情況文獻［12］在非視距情況下使用均方根時延拓展模型對TDOA 測量誤差糾正，再通過最小二乘獲得近似解，使用粒子群算法得出最優解，文獻［13］在NLOS 環境中使用粒子群算法，利用慣性權重的非線性調整策略進行定位。

由此，本文提出一種NLOS 和LOS 混合環境中的目標定位算法，首先通過AD 判別篩選出NLOS較小的測距結果，再通過粒子群算法得到目標位置初值，最后通過迭代最小二乘得到目標最終定位位置。仿真效果表明本文算法在較小計算量的情況下，提升了定位的精度。

2 PSO-LS算法

粒子群優化算法［14］（Particle Swarm Optimization，PSO）由Eberhart和Kennedy 于1995 年提出，是一種基于種群的隨機優化技術。PSO 模擬自然界中昆蟲、鳥群、魚群等的群集行為，這些群體按照一種合作的方式尋找食物，群體中的每個成員通過學習自身經驗和其他成員的經驗來不斷改變其搜索模式。

迭代最小二乘［15］（Iterative LS，ILS）是求解非線性最小二乘逼近問題的，可以用來作為目標定位的方法。通過不斷的迭代逼近目標位置。

Anderson-Darling test 通過對數據分布判別分析達到LOS 和NLOS 區分的效果。在得到一組測距數據后進行AD檢驗。檢驗結果符合要求則表明該組數據近似服從正太分布，可將該組測距視為近似LOS條件下測得，不符合要求則說明該組數據可視為在NLOS條件下測得。整體算法框架如圖1所示。

女人說完就主動伸出手來，我心里有種莫名其妙的沖動。我趕緊握住女人的手，女人的手很白很嫩，我緊緊地把它攥在手心里，女人并沒有反對，好像這白晰修長的手原本就該屬于我一樣。

圖1 算法流程

2.1 Anderson-Darling test（AD test）

LOS 環境和NLOS 環境下的距離公式如式（1）所示。存在一組測距數據D=[d1,d2,…,di,…,dM]，在視距情況下可近似視為服從高斯分布，而由于非視距誤差nnlos的不穩定性，dnlos不服從高斯分布。故可以通過測距數據是否近似服從正態分布區分視距環境和非視距環境。

由于實際情況中非視距誤差可能極大地影響測量結果的精度和準確性，通過AD 檢驗方法［4］對視距和非視距環境進行劃分，可以篩選出那些非視距誤差較小的一些測距組合，從而達到優化測距的效果。

由此可做如下假設H0:di～N(μ,δ2)，通過對距離進行標準化處理式（2）可得～N(0,1)。將處理結果作為標準化輸入進行AD計算得式（3）：

其中φ表示標準正態分布概率密度函數，F(Zj)表示其累計分布函數。評價標準CV計算如式（5）：

如果AD＞CV，則假設H0錯誤，說明該組測量距離存在較大非視距誤差，需要去除誤差較大項并重新測距。否則，將該組測量距離視為近似LOS環境下的測距，進入下一個環節的定位。

2.2 TDOA定位

TDOA 通過測量BS（base station）和MS（mobile station）之間的到達時間差來計算距離差，從而建立雙曲線方程。假設存在BS1,BS2,BS3三個定位傳感器，我們將其位置定義為x1=(X1,Y1),x2=(X2,Y2),x3=(X3,Y3)。MS 的實際坐標為(x0,y0)，估計坐標為=(x,y)。BSi和BSj到MS的距離差表示為

當BS 和MS 之間都是LOS 路徑且忽略噪聲偏差時，三條雙曲線方程將相較于一點，該點就是MS的實際位置(x0,y0)。當噪聲偏差和NLOS 誤差無法忽略時，三條雙曲線將會形成一個稱為可行范圍的區域，如圖2 所示。

圖2 TDOA的可行范圍

交點坐標U(Ux,Uy),V(Vx,Vy),W(Wx,Wy)通過求解式（1）中所示的雙曲方程得到。PSO 算法中目標函數［16］如式（8）所示：

由于MS(x,y)的估計坐標可以在NLOS 誤差和噪聲偏差引起的可行范圍內找到，使得目標函數值最小的解是MS 的估計坐標，于是原本定位問題轉換為了帶約束最優化問題，求得的估計坐標作為迭代最小二乘的初始值，進入下一步計算。

2.3 迭代最小二乘法（ILS）

上述定位問題中，本文通過測量距離差及實際距離差建立非線性最小二乘，如式（9）所示。以最小二乘結果作為損失函數，通過迭代最小二乘法進行目標定位求解。

更新迭代公式如式（10）所示：

3 仿真結果分析

3.1 仿真條件

本文采用Python對上述理論進行仿真，仿真環境如下：測量噪聲設定為方差為δ2的高斯分布，NLOS 為[0,U]的均勻分布。三個測量點BS 分別位于(0,0)(0,10)(5,)，待測點實際位于(5,5)，且預測位置表示為(x,y)。在得到MS 的估計位置后，根據式（14）計算均方根誤差：

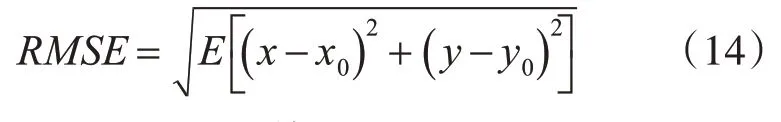
3.2 NLOS環境下不同算法定位效果

圖3 展示了在固定迭代步長k=0.01，迭代次數為100 的情況下，不同算法GA、PSO 及ILS 下NLOS誤差和RMSE 之間的關系。從圖中，可以看出隨著NLOS 誤差上界的增大，各個算法的RMSE 均逐漸增大。同時，相較于其余算法GA、PSO，ILS 算法的RMSE 值在相同NLOS 誤差上界時魯棒性更強。實驗結果表示ILS 可以較大的提升存在NLOS 誤差時定位的準確性。相較于GA，PSO 等方法，ILS 算法基于多次測量結果進行定位計算，在測量次數多時定位結果較為準確。然而，ILS 算法雖然對計算精度進行提升，但同時需要更多的計算量及帶來更多時延。

圖3 NLOS環境下不同算法定位效果

3.3 不同初值對ILS影響

如圖4 所示，使用五個不同點作為初始點運行ILS算法。其中，步長大小設置為0.1，NLOS誤差上界設置為50cm，待測點位于（5，5）。在不同初始值下，RMSE 隨迭代次數變化的圖像如圖4 所示。可以看出，隨著初始RMSE 誤差的增大，收斂時所需迭代次數增加。結果表明初始誤差越小，到達相同RMSE所需迭代次數越少。

圖4 不同初值對ILS影響

表1 顯示了到達相同收斂精度時，不同初始點之間的迭代次數關系。從表中數據可見，在RMSE達到相同0.1m 誤差時，較大的初始誤差將需要更多次的迭代。這一結果展示了選取初始值對于迭代算法的重要性，較為精確的初始值可以較大地減少迭代次數，這對目標定位的實時性有重要意義。

表1 不同初始點達到相同誤差迭代次數

3.4 不同步長對PSO_LS影響

由于上述原因，本文提出一種結合PSO 和ILS的新算法PSO-LS。該算法致力于提升定位的準確率的同時減少計算時延。圖5 顯示了PSO-LS 算法在不同步長下RMSE 隨迭代次數變化的變化曲線，實驗中NLOS 誤差上界設置為50cm。從圖中可以看出，步長越大RMSE 收斂越快，但穩定后的精度越低。步長越小，迭代穩定后的RMSE 值越小，但是需要更多的迭代次數。

圖5 不同步長對PSO_LS影響

結果表明步長需要在定位精度和收斂速度之間進行權衡選擇，通過改變步長可以提高定位精度并減少收斂時間。

3.5 可變步長對PSO_LS影響

圖6 展示了可變步長k 下RMSE 隨迭代次數的變化，可變步長的定義k如下列函數所示：

圖6 可變步長對PSO_LS影響

其中l表示迭代次數，隨著迭代次數的增加，可變步長k(l)隨著迭代次數減小。圖中展示了步長分別為固定步長0.01、0.002 與可變步長k(l) 時，定位RMSE 誤差隨迭代次數變化。圖中可以看出相較于固定步長0.01，可變步長k(l)可以達到更好的收斂精度。同時相較于固定步長0.002，達到相同定位精度時使用可變步長需要更少的迭代次數。仿真結果表明采用可變的步長選取可以使得收斂速度更快、精度更高。

3.6 非視距環境中PSO_LS定位

圖7展示了在不同NLOS上界誤差下分別采用PSO 和PSO-LS 算法，在同時迭代50 次后，最終定位誤差的結果示意圖。圖中可以看出，隨著NLOS誤差上界的增大，粒子群算法的定位誤差明顯增大，而PSO-LS 算法隨NLOS 誤差增大定位誤差變化相對不明顯。結果表明PSO-LS算法可以通過較小的計算量極大地提升定位的準確率。

圖7 非視距環境中PSO_LS定位

3.7 混合環境中AD檢驗對定位改進

圖8 展示了在NLOS 和LOS 混合環境中，采用AD檢驗法對定位性能的提升。仿真實驗組數據從150組LOS和150組NLOS數據中提取出滿足AD檢驗的一批數據。對照組采用等比率的LOS和NLOS數據，定位過程均使用PSO_LS 算法。其中NLOS的上界誤差設置為100cm。仿真結果表明，在混合環境中的測距采用AD檢驗可以較大提升定位的精度。

圖8 混合環境中AD檢驗對定位改進

本實驗提取滿足AD 檢驗測量數據方法如下。由于NLOS 誤差均為正值，考慮偏大的數值均有可能是存在NLOS 的測量數據，通過逐步刪除NLOS數據從而達到篩選測量數據的效果。對數據進行整體AD 判斷時，若數據不滿足近似正態分布假設則刪去其較大值并循環上述操作，若近似滿足正態分布則輸出該組數據。

4 結語

本文將粒子群算法與迭代最小二乘算法相結合，提出PSO-LS算法用于TDOA 室內定位優化，以消除非視距和噪聲偏差。主要流程為通過粒子群算法獲得定位初值，同時將通過AD 檢驗的測距結果作為最小二乘的輸入，再采用迭代最小二乘算法更新位置估計值。

仿真實驗研究了不同初值，步長下的定位精度和收斂速度，對AD 檢驗在混合環境中應用進行了研究。仿真結果表明，AD 檢驗能有效地從NLOS和LOS混合環境中篩選出誤差較小的項，從數據源上提升定位質量。適當的初始值可以減少計算量，變步長可以在較少的迭代次數下獲得較高的定位精度。研究結果可為室內定位提供有意義的參考。