基于BiGRU 的數據通信加解密模型的研究*

張仕忠 彭艷兵

（1.武漢郵電科學研究院 武漢 430070）（2.南京烽火天地通信科技有限公司 南京 210019）

1 引言

目前，神經網絡已成功應用于許多學科領域，通信及其保密通信作為神經網絡的重要研究領域之一，當然也已成為神經網絡的應用研究熱點，而密碼學技術作為保密通信中的關鍵技術，也一直受到重要的關注。從信息科學的角度出發，神經網絡和密碼學都屬于研究信息處理的學科，而隨著神經網絡被應用于越來越復雜的任務，自然也可以應用于端到端的任務，比如端到端的通信。密碼學主要就是確保信息的完整性和保密性，即明文只能從正常通信的密文中通過正常解密得到，而攻擊者無法從密文中得到有用的明文信息。因此將神經網絡與密碼學相結合便構成了神經密碼學這個綜合學科，作為綜合學科，神經密碼學能夠推動神經網絡和密碼學的共同發展［1～4］。

在密碼學中，明文和密文是作為具有復雜映射關系的數據對而存在的，而神經網絡根據自身的特征，是可以學習到明文和密文之間的映射關系的，因此可以選擇合適的深度學習模型來用于密碼學的研究。近年來，神經網絡在密碼學領域的應用頗多，2015 年Qin K 等提出關于兩種混沌神經網絡密碼算法的密碼分析［5］。2016 年Google Brain 團隊Abadi等利用以卷積神經網絡為核心的對抗神經網絡結構進行了安全通信方面的研究［6］。2019 年J Aayush Jain 等提出基于神經網絡的輕量級分組密碼分析［7］。

本文提出使用BiGRU 應用于數據通信中數據加解密模型的研究，即密碼算法的生成方式由神經網絡自動生成，不再使用傳統密碼學中的數論思想，并且利用神經網絡的黑盒性質來保證整個數據通信模型的通信安全性。通過以BiGRU 為核心的神經網絡結構進行整個模型的構建，并在同文獻［6］的Alice、Bob 和Eve 的N 位密鑰對稱加密系統方案相對比下，實現一個更加穩定的可正常加解密并能抗竊聽的數據通信模型。

2 研究方法

2.1 對稱密鑰加密體系

文獻［6］中提出基于對抗神經網絡的對稱密鑰加密系統，通信雙方Alice與Bob以及竊聽者Eve均以卷積神經網絡（CNN）為核心構建自身的神經網絡模型［8］。Alice 通過密鑰K（Key）對明文P（Plain-Text）進行加密，加密后生成密文C（Ciphertext）。然后，解密者Bob 與竊聽者Eve 均能夠獲取到完整的密文C。Bob 則是通過密鑰K 對密文C 進行解密，解密后獲得解密明文PBob。而Eve 則是在沒有獲取密鑰K 情況下對密文C 進行解密，從而得到猜測的明文PEve。在整個系統訓練的過程中，Alice 與Bob組成的加解密通信模型與Eve 的竊聽模型在對抗訓練過程中不斷互相優化，最終使得PBob與明文P盡量相等，即Bob 可以通過密鑰K 和密文C 可以解密出與明文幾乎相同的內容。而PEve與明文P 之間的差異盡量大，即PEve最終會近似等于一個隨機猜測的結果。對稱加密體系如圖1所示。

圖1 對稱密鑰加密體系圖

2.2 GRU模型

由于傳統的循環神經網絡（RNN）在處理序列時會出現嚴重的梯度消失問題，而為了解決梯度消失問題，Hinton 等提出了長短時記憶神經網絡（LSTM）［9］。但是隨著LSTM 的不斷被應用，有關于LSTM 的訓練時間長、參數較多、內部計算復雜等缺點也逐漸的暴露了出來。為了解決這些缺點，Cho 等在2014 年進一步提出了更加簡單的、將LSTM 的單元狀態和隱層狀態進行合并的、還有一些其他變動的GRU（Gate Recurrent Unit）模型［10］。GRU 又稱門控循環單元，整個單元主要是由更新門和重置門兩個門組成，而在計算隱藏狀態方面與傳統的循環神經網絡相比也因此大有不同。GRU結構具體如圖2所示。

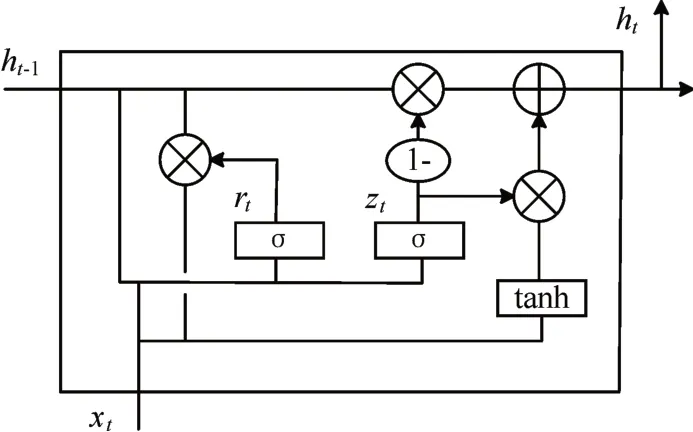
圖2 GRU結構圖

圖2 中的xt是輸入數據，ht是GRU 單元的輸出，rt是重置門，zt是更新門，rt和zt共同控制了從ht-1隱藏狀態到ht隱藏狀態的計算，更新門同時控制當前輸入數據和先前記憶信息ht-1，輸出一個在0～1之間的數值zt，zt決定以多大程度將ht-1向下一個狀態傳遞。具體的門單元計算公式為

其中：rt表示t時刻的重置門；zt表示t時刻的更新門；σ是Sigmoid 函數；Wz，Wr，W分別為更新門，重置門，以及候選隱含狀態的權重矩陣；為t 時刻備選激活狀態；ht為t 時刻的激活狀態；ht-1為（t-1）時刻的隱層狀態。

由于單向的GRU 只能得到前向的上下文信息，而忽略了后向的下文信息，有時會由于信息獲取不足，從而使得GRU 的實際應用效果不好。而BiGRU（雙向GRU 神經網絡）可以從前向和后向上同時獲取上下文信息，從而提高訓練過程中的特征提取的準確率。另外還可以利用BiGRU 提高整個神經網絡模型的響應速度。因此本文采用BiGRU來構建模型，BiGRU結構如圖3所示。

圖3 BiGRU結構圖

2.3 基于BiGRU的數據通信加解密模型

本文的數據通信體系采用圖1 所示的對稱密鑰加密體系，然后采用以BiGRU 為核心的神經網絡單元來構建整個模型的網絡結構［11～13］。由于傳統的密碼函數一般是不可微分的，而這與深度神經網絡的中隨機梯度下降是相矛盾的，所以直接用神經網絡去學習密碼學的傳統數論理論的函數是比較困難的。但是神經網絡是可以去學習如何保護數據通信過程中的數據機密性，即在通信過程中，直接由神經網絡自身去學習數據通信的加解密過程，整個過程中無需為通信模型規定特定的密碼學算法，從而保證了數據通信的安全性和機密性。

在通過對明文密文對的特征分析后，明文密文數據對的關系其實可以轉換成文本序列問題，從而通過RNN 在處理文本序列問題上的優勢，學習明文密文數據對之間復雜的映射關系，從而實現正常且安全的數據通信加解密模型［14～15］。模型結構圖如圖4所示。

圖4 模型結構圖

圖中模型總共為三層，第一層為輸入層，即輸入需要進行訓練的已經預處理好的數據。第二層為隱含層，由BiGRU 加上激活函數再加上一個BatchNormalization 層構成。第三層為輸出層，由一個4N×N 的全連接層構成。下面對模型的Alice、Bob以及Eve三個組件的網絡結構進行構建。

Alice網絡構建：

1）明文P 與密鑰K 橫向拼接作為Alice 的輸入（設明文與密鑰長度均為N）；

2）輸入層的輸入傳入BiGRU 網絡中，輸出經過激活函數tanh［16～17］；

3）經過激活函數的輸出傳入BatchNormalization層［18］；

4）經過BatchNormalization層的輸出傳入4N×N全連接層；

5）全連接層輸出的結果為密文C。

Bob網絡構建：

1）密文C 和密鑰K 橫向拼接作為Bob 的輸入（設密文與密鑰長度均為N）；

2）網絡結構與Alice一致；

3）輸出結果為Bob所解密的明文結果PBob。

Eve網絡構建：

1）密文C單獨作為Eve的輸入；

2）網絡結構與Alice一致；

3）輸出結果為Eve所解密的明文結果PEve。

2.4 模型損失函數設計

關于模型的損失函數，本文采用Bob 生成的明文PBob與實際明文P 的L1 距離，以及Eve 生成的明文PEve與實際明文P 的L1 距離作為模型的損失函數標準。設實際明文P 和解密明文Pd的長度均為N，本文使用L1距離來定義兩者之間的距離公式：

其中|Pi-Pdi|代表解密明文Pd與實際明文P 在每一位上的誤差值，而d（P，Pd）代表明文P 與解密明文Pd的N 位誤差的平均值。Eve 作為解密的組件，它的目標就是盡可能準確地重建明文P 的值。因此它的損失函數定義為

因為Alice 與Bob 之間需要保證準確的數據通信，而且它們也要對Eve 的竊聽行為具有抵抗能力。為了達到最優的效果，本文結合Bob 和Eve 兩者訓練的損失最優值來定義Alice 和Bob 的聯合損失函數：

其中式（7）的d（P，PBob）代表Bob 所得的解密明文PBob與實際明文P 的L1 距離，（1-LEve）2代表Eve 的Loss對Alice與Bob這兩者通信的影響，但是在整個模型定義中，Eve 的解密效果不應該比隨機猜測做得更好，即當Eve所得明文PEve的N/2消息位是正確的且另外N/2 消息位是錯誤的時，Eve 這個組件對整個模型的影響力是最小的。之所以選擇二次公式（8），是為了當Eve 解密出正確明文時，使得Eve給整個模型帶來更少的損失影響，從而提高訓練的魯棒性。

3 實驗驗證

3.1 實驗環境

本文模型采用的編程語言為Python 3.6，深度學習框架為Pytorch，運行的操作系統為Linux，在NVIDIA GTX1080Ti上進行實驗。

3.2 實驗參數設置

實驗中輸入的明文P 和密鑰K 的位數N 取值為16，并且P 和K 中每一位隨機取值為-1 或者1。訓練的batchsize 設置256，epoch 為10000。實驗中Alice、Bob 和Eve 均采用Adam 優化器進行模型優化，Adam 算法具有適用于基于適應性低階矩估計并且能夠解決包含高噪聲或稀疏梯度問題等優點［19～20］。學習率固定設置為0.001。因為訓練過程中，Alice、Bob 和Eve 三個組件會互相影響，設置固定的學習率可以讓它們三者保持對彼此的變化做出較強的響應，整個模型在保證Alice 和Bob 的通信趨于穩定的同時還對Eve的竊聽具有抵抗能力。

3.3 實驗結果與分析

3.3.1 訓練結果與分析

對于一次成功的訓練，Bob 的重建明文誤差和Eve 的重建明文誤差隨著訓練步驟數的變化曲線如圖5所示。

圖5 Bob與Eve的重建誤差訓練圖

圖5中的每個點是256個示例的平均誤差。理想的訓練結果是Bob 的重建明文誤差降到零，Eve的重建明文誤差達到8 位（即錯誤位數為一半）。如圖的訓練例子中，兩個組件的重建誤差剛開始都很高，但是經過一定的訓練步驟后，Bob 的訓練誤差開始不斷減小，Alice和Bob之間能夠進行有效的交流，同時，Eve 的解密能力也在提升。然后，在1000 步左右，Eve 的訓練誤差開始回升，這是因為Eve 在向隨機猜測的目標方向前進，而Bob 的重建誤差不斷下降，逐漸趨近于0。經過約3000步，Bob的重建誤差基本接近于0，而且Eve 的誤差也在7位到8 位之間浮動，接近隨機猜測的結果。繼續進行訓練，Bob和Eve的重建誤差都基本趨于穩定。

3.3.2 測試結果對比與分析

將之前基于CNN 的數據通信模型［6］和本文的基于BiGRU 的數據通信模型對比加解密效果。取epoch為1000進行測試，基于CNN 的數據通信模型測試結果如圖6所示，基于BiGRU 的數據通信模型測試結果如圖7所示。

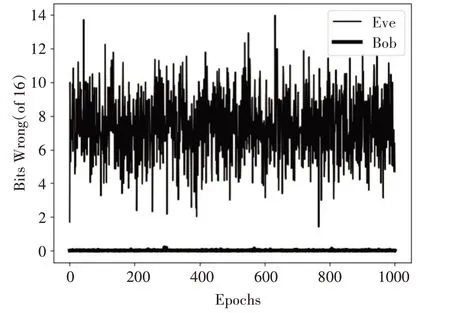
圖6 基于CNN的通信模型測試效果圖

圖7 基于BiGRU的通信模型測試效果圖

從兩個模型的測試對比效果來看，兩者在Bob的解密能力方面差別不大，基本都能實現與Alice的正常通信，基于CNN 的通信網絡的解密效果稍微會有些波動，而基于BiGRU 的通信網絡相對更加穩定。關于Eve的解密能力對比，基于CNN的通信的Eve解密誤差波動幅度較大，在16位明文的前提下，差異值最高到12 位以上，而最低則是快接近0 位，可以看出該模型中的Eve 是能竊取到大量信息的，模型的抗竊聽能力存在不足。而基于BiGRU的通信網絡的Eve 解密誤差基本穩定在7 位左右，接近隨機猜測的效果。說明基于BiGRU 的數據通信模型比基于CNN 的數據通信模型具有更好的抗竊聽能力。

4 結語

本文提出一種基于BiGRU 的數據通信加解密模型，通過循環神經網絡來學習密碼學中的明文密文對的映射關系，從而通過神經網絡實現端到端通信的加解密過程。并且與之前的基于卷積神經網絡的數據通信模型進行對比，本模型能夠在實現正常通信的前提下，并且具有更好的抵抗竊聽的能力。

關于神經網絡在數據通信加解密的應用方面，本文提出了一種新的方案，并通過實驗驗證了可行性。隨著信息的安全通信問題受到越來越多的關注，信息的加解密問題已然成為當前研究的熱點，因此研究神經網絡在數據通信領域的應用有著十分重要的價值和意義。