基于IT2SFNN 的多關節機械手自適應反演控制*

馬歡歡 趙樂

（貴州大學機械工程學院 貴陽 550025）

1 引言

在智能制造時代，機械手兼具人和機械的優點，被廣泛應用于汽車制造和航空航天等諸多領域，如何控制機械手的高效運作成為一個研究熱點［1～3］。但機械手在作業過程中，運動狀態不斷變化，具有時變性；內部摩擦和未知干擾的存在又使機械手具有一定的不確定性，因此在模型模糊的前提下，傳統的控制方法和手段很難使機械手關節在快速追蹤到期望軌跡的同時保持良好的控制精度。

為了取得理想的控制效果，人們嘗試將更多的控制方法引入到機械手系統中。PID 控制器由于成本低、結構簡單和良好的控制性能被采納［4～6］，但由于機械手為強非線性的系統，而PID 控制器更好地適用于線性系統和微非線性的系統，因此這類方案的控制效果并不理想。鑒于此，計算力矩的非線性控制器、自適應控制和滑模控制等非線性控制方法被應用于機械手系統。W.Peng等針對機械手設計的非線性控制器性能良好［7］，但該控制器是建立在足夠精確的模型之上的，而機械手在實際工作過程中，參數時刻變化，模型十分模糊，因此該設計方案有一定的局限。滑模控制針對時變性和非線性的機械手系統，表現出良好的控制性能［8～10］，但是其存在抖振的問題，可能激發機械手建模中被忽略的高頻動態，從而導致系統崩潰。自適應控制因其抗干擾等優點在多關節機械手控制中應用廣泛［11～13］。

近些年，自適應反演法作為控制不確定非線性系統的有效工具被引入到機械手控制系統［14～15］。但是模型的不確定性以及未知的擾動為反演控制帶來了難題。神經網絡的出現很好地彌補了這一缺陷，改善了反演控制的性能。由于神經網絡具有逼近任意非線性函數的優點，因此被廣泛應用于逼近機械手模型中的慣性力矩陣和離心力與哥氏力等。二型順序模糊神經網絡（T2SFNN）作為模糊理論與神經網絡的產物，兼具二者的優點［16］，表現出更好的學習能力。

基于上述學者對機械手的研究成果，在反演控制框架內融入神經網絡，利用區間二型順序模糊神經網絡（IT2SFNN）處理機械手干擾未知和模型模糊的問題，在此基礎上采用反演控制方法設計控制器，并針對未知干擾項和逼近誤差設計了魯棒補償項以獲得更理想的控制效果。

2 動力學模型

多關節機械手的動力學模型可表示為如下非線性微分方程［17］：

機械手的動力學模型具有以下特性［18］：

3）未知擾動τd滿足‖τd‖≤τM，τM為一正常數。

隨著機械手關節數目的增加，其動力學模型的耦合性和非線性增強。另外，動力學模型的時變性和不確定性為實時獲取精確的模型參數帶來了困難，這里將利用IT2SFNN來解決這個難題。

3 IT2SFNN

本節對IT2SFNN［16］進行介紹。IT2SFNN 結構如圖1 所示，共有5 層：輸入層、模糊化層、隸屬度層、模糊規則層和輸出層。

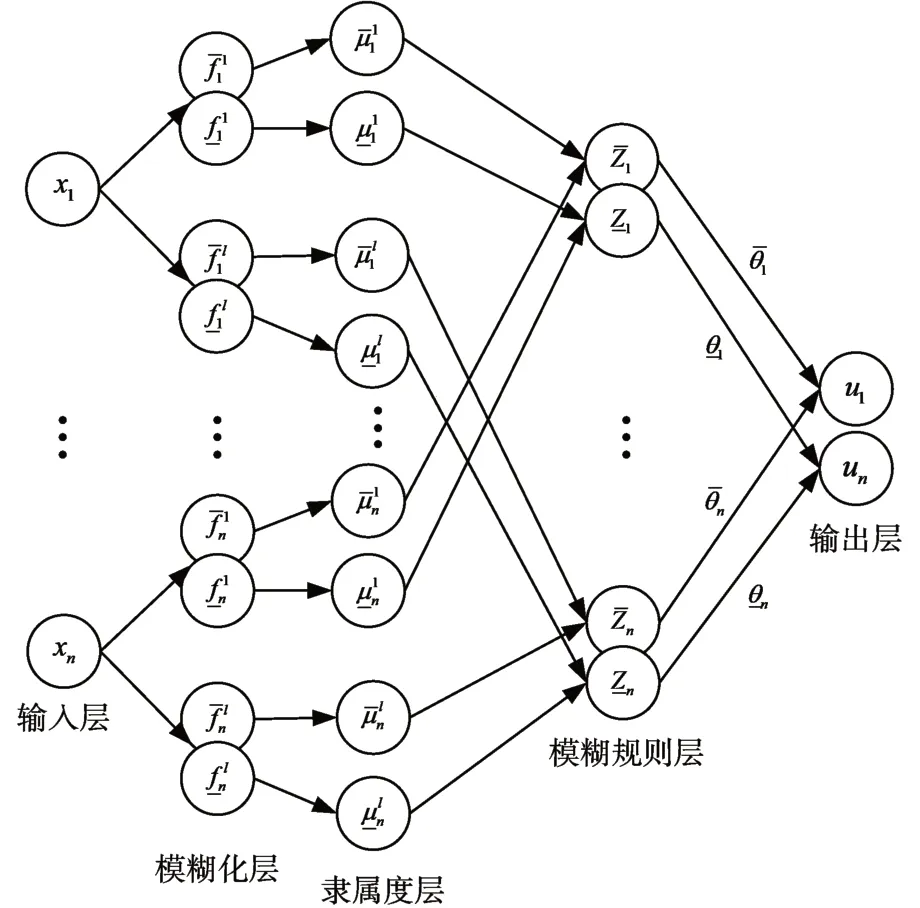
圖1 IT2SFNN結構圖

隸屬度層：此層對上層的輸入值繼續進行模糊化處理，采用區間二型高斯隸屬度函數，如圖2 所示。與fi相對應的高斯型上限隸屬度函數和高斯型下限隸屬度函數分別為

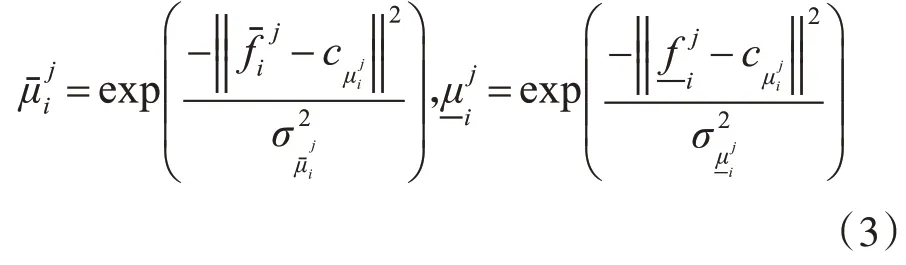
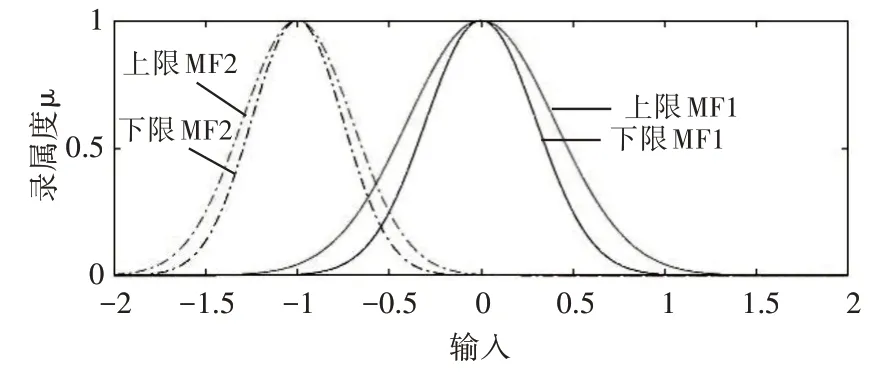
圖2 區間二型隸屬度函數

模糊推理層：IT2SFNN 中的模糊規則設計如下：

輸出層：IT2SFNN 的輸出值u取上限輸出與下限輸出的平均值即：

4 控制器設計

為了解決上述提到的問題，基于自適應反演法分三步設計控制器，使機械手各關節在快速進入期望軌跡的同時保持高的控制精度，取得理想的控制效果。

第一步：定義跟蹤誤差為

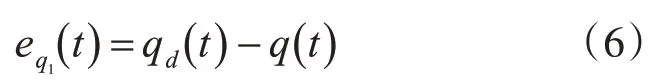
式中，qd為期望跟蹤角度。

定義第一個Lyapunov方程為

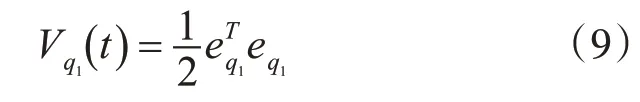
第二步：令

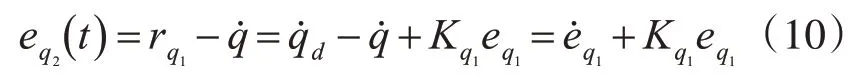
分別對式（9）和式（10）求導得

對式（14）求導得

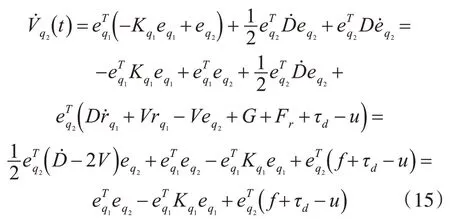
式中：

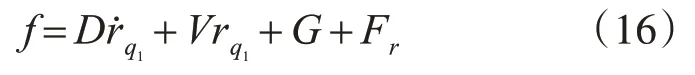
第三步：設計控制輸入

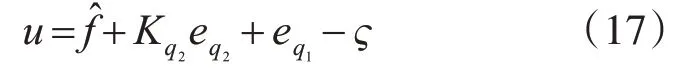
式中?為針對IT2SFNN 逼近誤差ε和不確定干擾τd設置的魯棒補償項。將魯棒補償項?設計為

其中‖ε‖≤εmax，‖τd‖≤τmax，η＞0。

將式（17）代入式（15）得

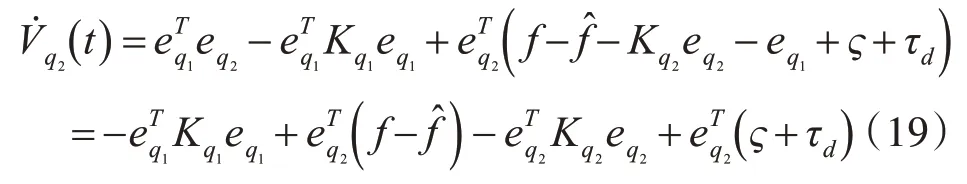
定義θo為理想逼近常量，θ為實際逼近常量，令-θ。

定義第三個Lyapunov方程為

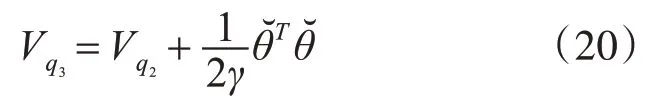
對式（20）求導得

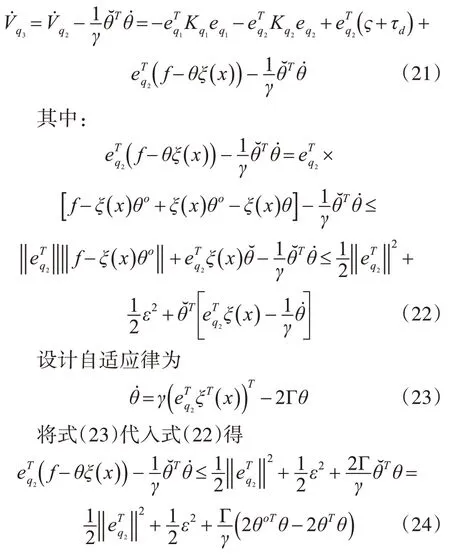
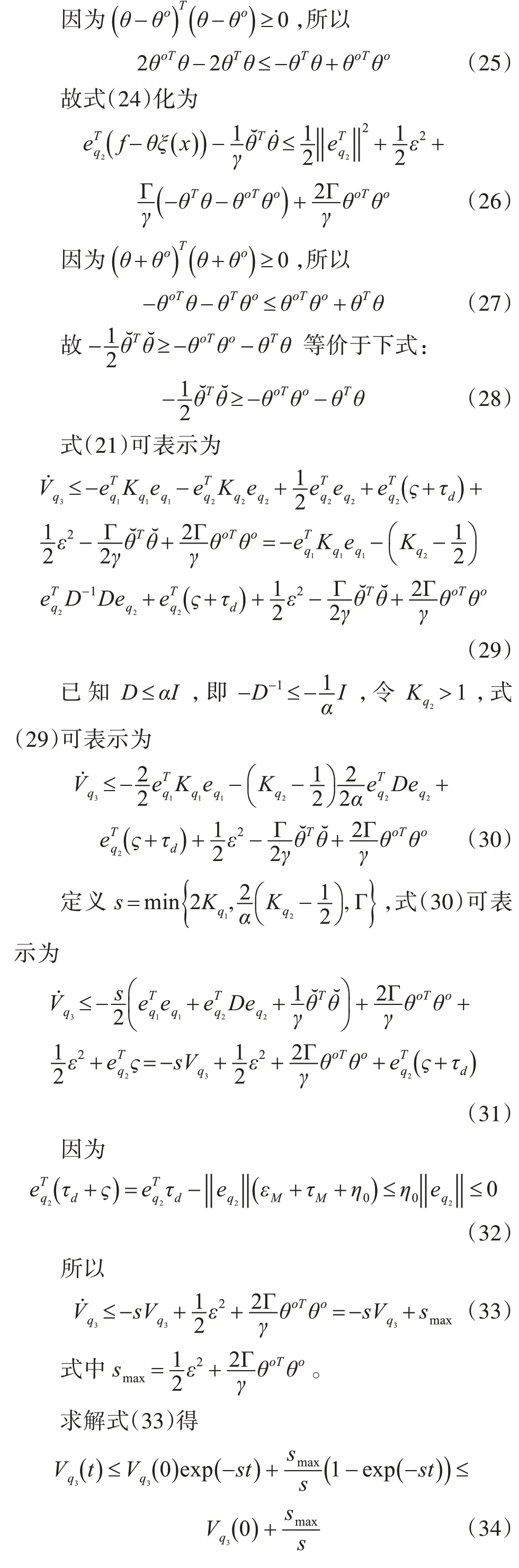
5 數值模擬

這里以二關節機械手為仿真對象，模型中

5.1 位置跟蹤分析

圖3 為兩關節的位置跟蹤仿真結果，從中可以看出，所設計控制器能使關節1 和關節2 在0.1s 內跟蹤到期望的位置信號，快速進入理想軌跡，足以達到大部分機械手的工作要求。圖4 為兩關節的跟蹤誤差，從中可以看出，系統達到穩態后，關節1的跟蹤誤差可以穩定在0.01rad以內，關節2的跟蹤誤差可以穩定在0.005rad 以內，表明所設計的控制器具有良好的控制精度。

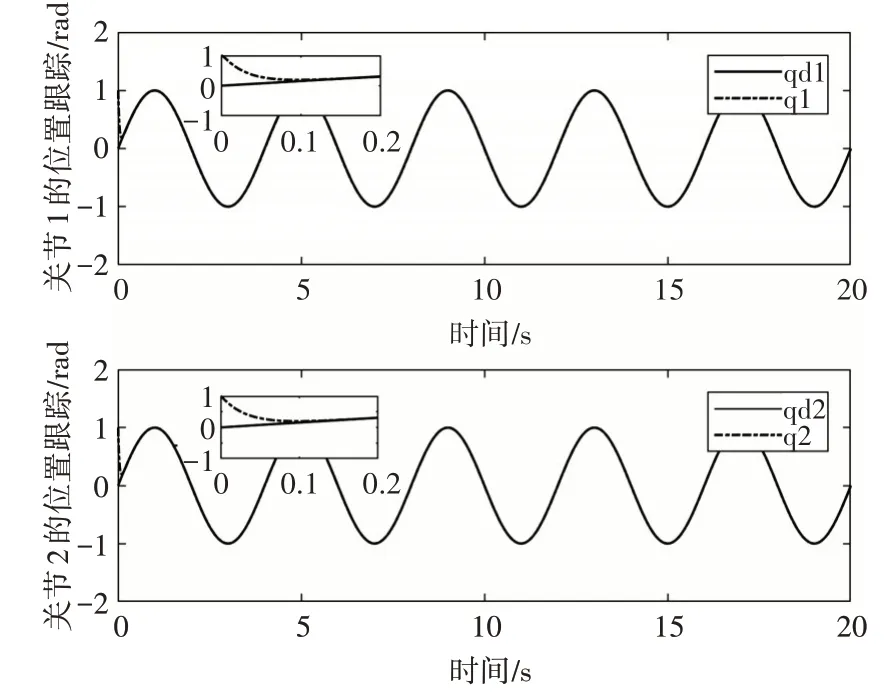
圖3 位置跟蹤

圖4 跟蹤誤差

5.2 魯棒性分析

仿真過程中，分別取干擾τd1=[0.4 sin(t) 0.4 sin(t)]T，τd2=[0.15 sin(t) 0.1 5 sin(t)]T與τd=[0.25 sin(t) 0.2 5 sin(t)]T時的跟蹤誤差和控制輸入作比較，得到圖5和圖6。從圖中可以看到，隨著干擾力矩的變化，兩個關節的跟蹤誤差維持在極小的變化范圍內，控制輸入也僅有微小浮動，即表明所設計的控制器對于不同的外界干擾表現出較強的魯棒性。

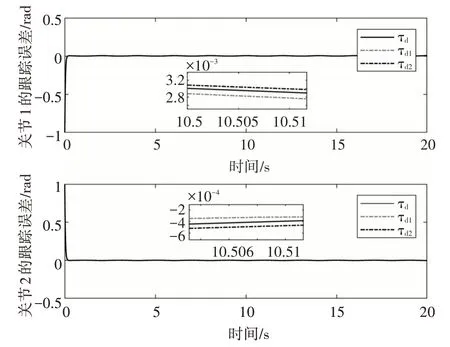
圖5 不同干擾下的跟蹤誤差

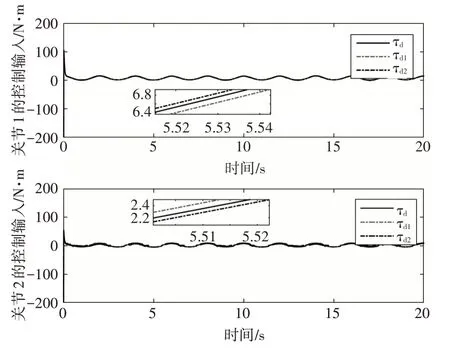
圖6 不同干擾下的控制輸入

6 結語

結合多關節機械手時變性和不確定性的特點，提出了一種自適應的反演控制策略。利用IT2SFNN 獲取機械手模型中不確定部分的估計值，基于李亞普諾夫穩定性理論設計了控制律和自適應更新律，并且在保證閉環系統穩定性的前提下，設計了魯棒補償項。仿真表明，所設計的控制器能保持良好的控制精度并快速跟蹤到期望信號，且魯棒性良好。