直線電機推力波動補償技術

沈海濤, 汪 奇, 吉曉凱, 張 凱, 周 原

(蘇州維嘉科技股份有限公司，江蘇 蘇州 215000)

0 引 言

永磁同步直線電機因其推力密度高、功耗低、響應速度快等特點而被廣泛應用于印刷電路板(PCB)鉆孔機、鑼機、分板機、鉆孔檢測等高速、高精度數(shù)控系統(tǒng)，并得到了國內外學者的關注與研究[1-4]。

因初級鐵心開斷引起的邊端力和因齒槽效應引起的齒槽力(合稱磁阻力)[5-7]是引起直線電機推力波動的主要因素。而推力波動是直線電機產生振動和噪聲的主要原因，特別是在低速運行時，推力波動會導致運動控制跟隨誤差變大[8]。因此，國內外學者對直線電機的推力波動進行了大量的研究。

文獻[9]通過分析永磁同步直線電機推力波動的機理，指出推力紋波、齒槽效應和端部效應是引起永磁同步直線電機推力波動的最主要原因，探討了減小永磁同步直線電機推力波動的技術措施。文獻[10]采用半無限單端結構建立了由邊端效應引起的磁阻力分析模型，并提出了優(yōu)化初級長度從而降低磁阻力的原理與方法。文獻[11]提出一種將磁極錯位與V型磁極相結合的優(yōu)化方法來改善其性能。同樣地，也有學者在控制算法上對直線電機推力波動進行分析、抑制[12-13]與補償[8,14-15]。

綜上，本文提出一種直線電機推力波動補償?shù)姆椒ǎ砸慌_6槽8極電機為研究對象，結合解析計算理論基礎與有限元建模，分析并歸納永磁直線電機邊端力與齒槽力的影響因素與一般規(guī)律。合理設置補償器關鍵參數(shù)，有效補償傳統(tǒng)永磁直線電機磁阻力。通過試驗，驗證該補償方法對直線電機推力波動抑制的正確性與精確性。

1 邊端力分析與計算

考慮直線電機鐵心開斷的緣故，直線電機左右兩端分別受到了兩個邊端力，其效果滿足磁阻最小原理，即磁通總是沿著磁阻最小的路徑閉合[15]。

1.1 直線電機邊端力分析

對于直線電機邊端力分析，其模型等效于無槽直線電機[10]，如圖1(a)所示，其中初級鐵心截面等效為一個矩形，因不存在齒槽結構，所以實現(xiàn)了分離齒槽力，僅分析直線電機邊端力。初級鐵心在不同位置受到的邊端力不同，且分別受到兩側端部的力Fend_L和Fend_R，由于次級永磁體周期排列，相應的邊端力就是次級極距的周期函數(shù)。同理補償器模型亦可看作無槽直線電機，如圖1(b)所示，其邊端力特性與直線電機相同，唯一區(qū)別在于兩者之間位置不同導致存在相位差，且補償器尺寸更小。

圖1 邊端力分析等效模型

為簡化解析計算過程，作如下假設：

(1) 假設鐵心磁導率無窮大，且不考慮飽和問題；

(2) 忽略漏磁，即漏磁系數(shù)σ=1；

(3) 永磁體的相對磁導率為1，也就是和真空狀態(tài)保持一致；

(4) 只考慮法相磁場，不考慮運動方向和鐵心疊壓方向磁場變化。

根據(jù)電磁場相關理論可知，單位體積的氣隙磁場儲能為

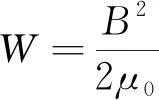
(1)

式中：B為氣隙磁密；μ0為真空磁導率。

因此對于直線電機，根據(jù)虛位移原理可得，直線電機左側邊端力為

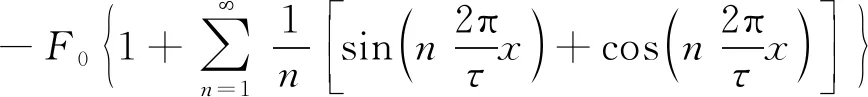
(2)

且有：

(3)

式中：La為電機初級鐵心疊厚；δ為電機氣隙長度；C為初級鐵心長度;Br2P為2P次電機氣隙磁密；τ為極距(N-S);kc為電機氣隙系數(shù)。

同理，將x′=x+Δx代入式(2)(Δx=C-kτ，k為整數(shù))，同時考慮右端力方向為正，因此可以得到右端部力為

Fend_R(x)=

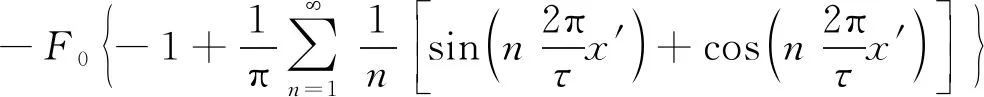
(4)

因此直線電機邊端力為

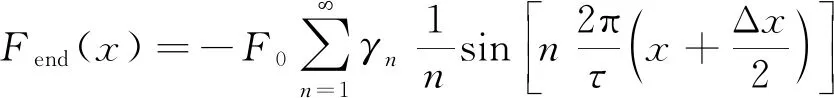
(5)

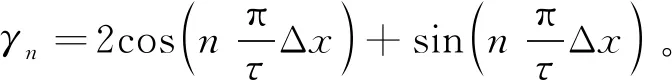
根據(jù)直線電機邊端力解析式(5)可得如下結論：

(1) 邊端力的基波頻率為1/τ，即直線電機邊端力頻率為電機運行頻率的兩倍頻；

(2) 當Δx=ατ時，其中α為整數(shù)，電機合成邊端力幅值最大；

(3) 當Δx=(2m-1)τ/2時，其中m為正整數(shù)，電機合成邊端力幅值最小，其基波幅值理論為0。

圖2所示為無槽電機邊端力幅值在Δx=(0～2)τ范圍內的有限元和解析計算結果。由圖2可見，邊端力的基波頻率為1/τ，且仿真結果和解析計算結果基本一致。為了獲得最低的邊端力以及最短的直線電機長度(直線電機長度會影響行程)，因而Δx=τ/2，即電機長度(初級鐵心長度)C=kτ+τ/2。

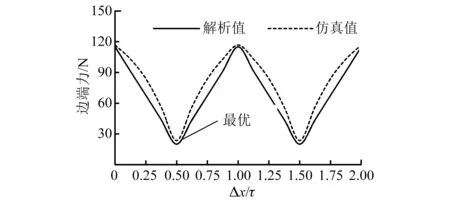
圖2 無槽電機邊端力幅值

1.2 補償器邊端力分析

為了能抵消直線電機產生的邊端力，因而期望補償器能產生一個與直線電機邊端力頻率相同、幅值相同、相位相反的邊端力。

補償器模型如圖1(b)所示，同理補償器亦可看作是一個無槽直線電機，因此其邊端力為

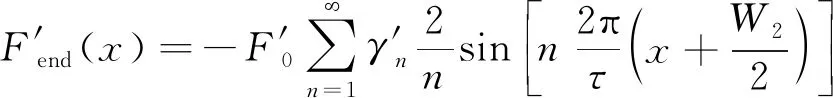
(6)

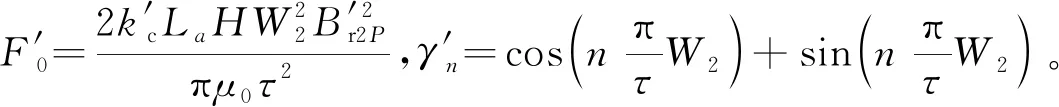
式中：H為補償器氣隙長度;W2為補償器長度;B′r2P為2P次補償器氣隙磁密;k′c為補償器氣隙系數(shù)。

顯而易見補償器邊端力與直線電機具有相同的頻率和分布特性，邊端力分布與圖2類似。考慮到更小尺寸的補償器產生更大的邊端力F′end用以抵消直線電機產生的邊端力Fend，因此參見圖2，補償器最佳長度為W2=τ。

圖3所示為直線電機及其補償器等效模型，其中補償器無齒槽結構。根據(jù)上述分析，此結構補償器可以產生一個與電機邊端力波長τ相同的邊端力諧波，因而只需補償器產生的邊端力諧波與電機的幅值相同，相序相反。

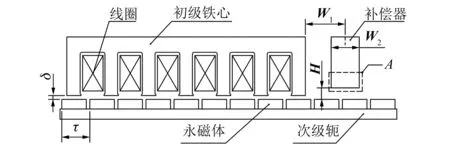
圖3 直線電機及其補償器等效模型

根據(jù)式(5)與式(6)，令∠Fend-∠F′end=180°得直線電機與補償器中心線之間的距離W1為

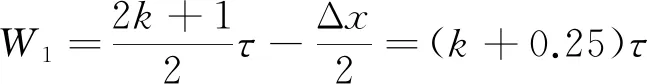
(7)

因W1≥W2/2，綜合考慮電機初級總長度，最佳的距離在k=1時，W1=5τ/4。

同理，令|Fend|=|F′end|，可得補償器氣隙長度H為

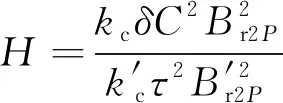
(8)

2 齒槽力分析與計算

由初級鐵心齒槽結構和永磁體相互作用產生的齒槽力，是永磁直線電機的另一重要參數(shù)，其存在同樣能造成電機的推力波動，進而產生速度波動、振動和噪聲。

2.1 直線電機齒槽力分析

與旋轉電機齒槽轉矩類似，直線電機齒槽力是電機在不通電的情況下，永磁體和齒槽間的相互作用力，其齒槽力表達式為[16-20]

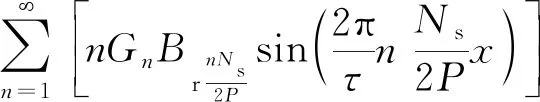
(9)

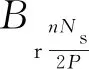
2.2 補償器齒槽力分析

將補償器同樣開出齒槽結構，如圖4所示。其齒槽力表示如下：

圖4 電機及補償器(帶齒)模型

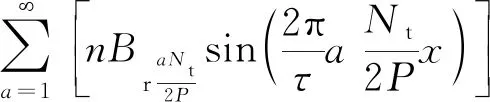
(10)

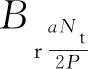
前面分析到，補償器最佳長度為W2=τ，即對于補償器，其極對數(shù)2p=1，因此式(10)中的整數(shù)a最小值為1。也就是說，補償器齒槽力基波次數(shù)與其齒數(shù)Nt一致。此時公式(10)可改寫為

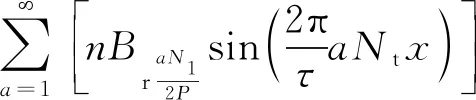
(11)

表1為不同單元電機補償器齒數(shù)匯總，從表1中可發(fā)現(xiàn)補償器齒數(shù)與單元電機初級齒數(shù)相等。

表1 不同單元電機補償器的齒數(shù)

3 仿真結果與分析

為驗證上述解析方法的正確性與準確度，以6槽8極電機為例，如圖4所示，對電機進行有限元仿真分析，電機與補償器基本參數(shù)見表2。其中6槽8極電機單元電機為3槽4極電機，參見表1，Nt=3。

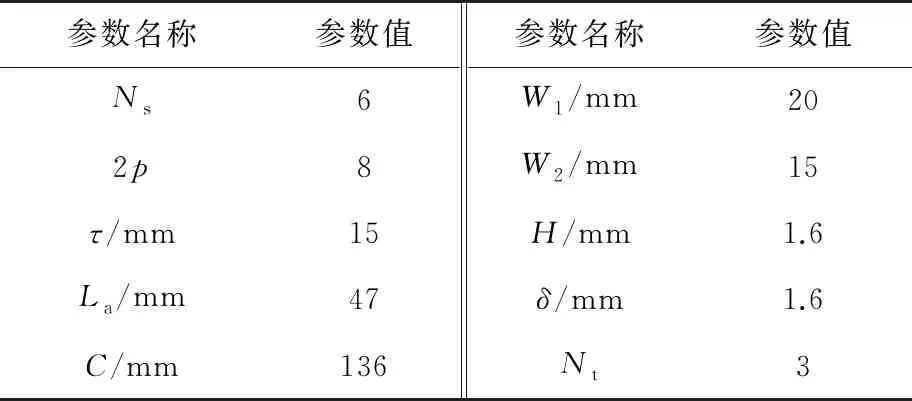
表2 電機與補償器參數(shù)

3.1 邊端力仿真計算

前述提到，在分析邊端力時，可將電機和補償器均看作無槽直線電機，如圖1所示。

圖5(a)為單獨直線電機與補償器邊端力有限元仿真和解析計算結果，可以看出在一個電周期2τ內，電機與補償器邊端力均波動了2次，也就說明邊端力波長為τ，與前述分析結果一致。同時可以看出直線電機邊端力與補償器邊端力相位相反，因而能起到抑制電機邊端力的作用，且解析結果與有限元仿真結果基本保持一致。

圖5(b)為搭配所述補償器后，直線電機合成邊端力有限元仿真與解析計算結果。解析計算合成邊端力為0，而仿真數(shù)據(jù)仍含有幅值為1.3 N的4次諧波，主要原因是解析計算只計算了2次諧波，而有限元仿真還包含4次、6次、8次等諧波。但是從效果上看，邊端力23.6 N降低到1.2 N，降幅高達94.9%，效果顯著。

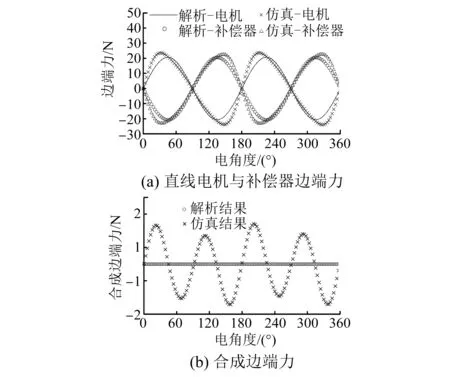
圖5 邊端力計算曲線圖

3.2 齒槽力仿真計算

對直線電機齒槽力進行仿真分析，需對仿真模型作如下設置，如圖6所示，即設置周期邊界，此時可忽略動子鐵心開斷引入的邊端力。同樣地對補償器亦作類似設置。

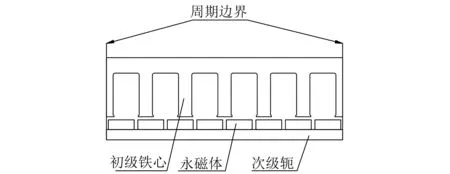
圖6 齒槽力仿真模型

圖7(a)為單獨直線電機與補償器齒槽力有限元仿真和解析計算結果，可以看出，6槽8極直線電機在一個電周期2τ內，齒槽力周期數(shù)為6，即符合前述分析一個極距τ內，齒槽力周期為nNs/2P=4×6/8=3。且補償器齒槽力周期同樣滿足上述分析。但補償器齒槽力幅值較直線電機齒槽力小得多，具體見圖7(a)和圖7(b)。圖7(c)為直線電機與補償器合成齒槽力，齒槽力仿真數(shù)據(jù)從5.5 N降低為4.4 N，僅降低20%，結合式(7)和式(8)，可以發(fā)現(xiàn)齒槽力幅值與直線電機初級長度C(對于補償器為W2)正相關，而本文中C?W2。因此，補償器對齒槽力削弱效果不明顯，且解析結果與有限元仿真結果基本保持一致。

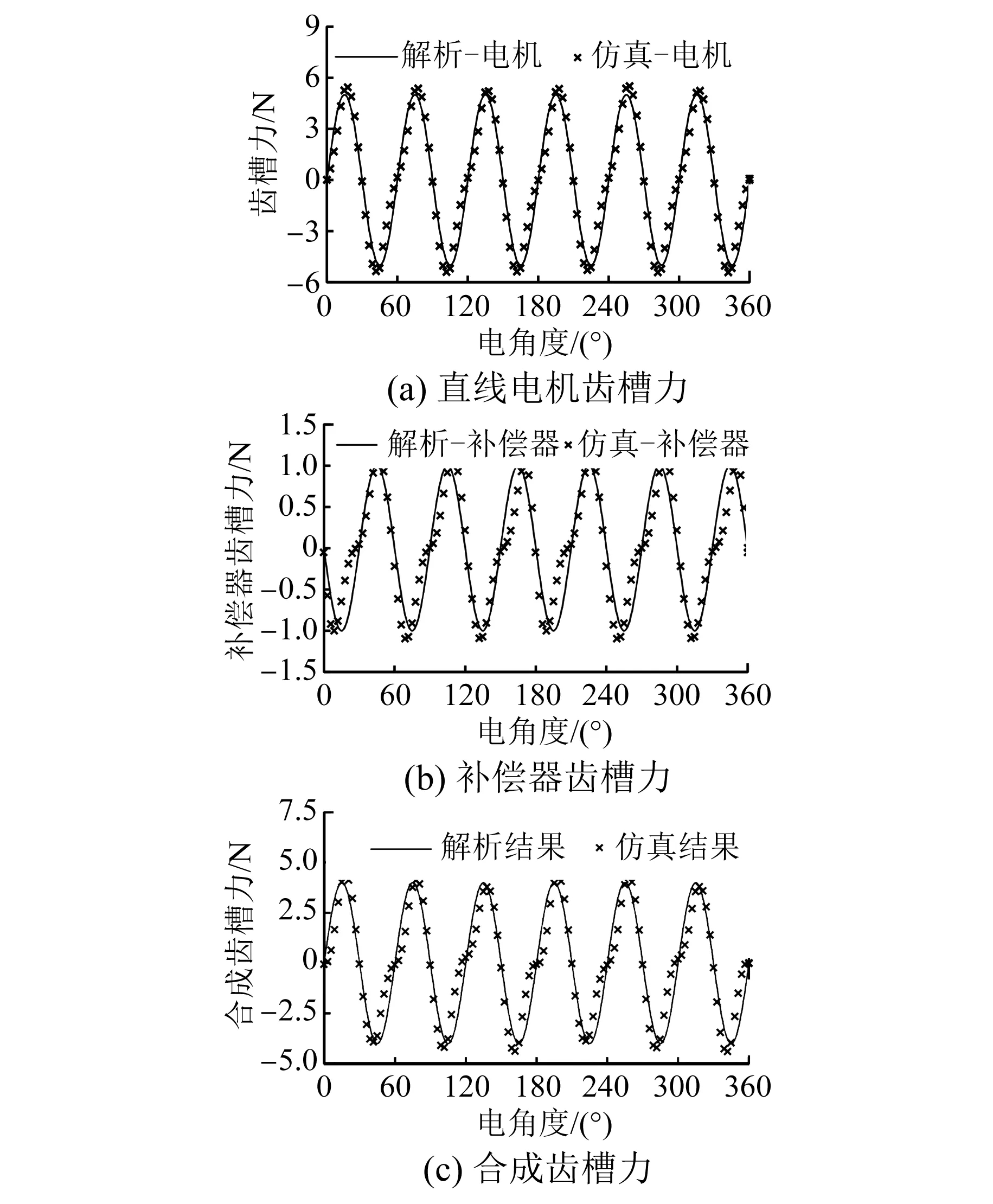
圖7 齒槽力計算曲線圖

3.3 磁阻力仿真計算

圖8為補償前后(模型如圖4)直線電機磁阻力有限元仿真與解析計算結果。可以看出，補償前后，直線電機磁阻力仿真數(shù)據(jù)從23.9 N降到了7.2 N，補償效果達到69.9%，十分顯著。解析結果與有限元仿真結果基本保持一致，其中補償前仿真數(shù)據(jù)較解析數(shù)據(jù)大的原因在于解析僅對邊端力的2次諧波、以及齒槽力的6次諧波進行分析，而仿真數(shù)據(jù)包含其他高次諧波。

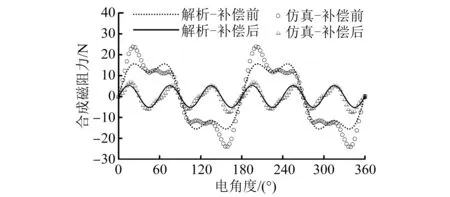
圖8 6槽8極直線電機合成磁阻力波形

4 試驗驗證

為了驗證解析計算與有限元分析的合理性與準確性，利用直線電機測試臺并配合高精度力傳感器，分別對測試臺、電機、補償器以及搭配補償器的直線電機磁阻力進行了測試。測試數(shù)據(jù)參數(shù)如表3所示。圖9(a)所示為對拖電機拉著被測電機安裝板情況下的測試臺自身的磁阻力波形，分為正、反兩個方向，因為對拖電機本身同為有鐵心直線電機，同樣具有磁阻力，同時因為測試臺的抖動、摩擦力不均勻等，所以此時磁阻力波形為非理想恒值波形，具有些許波動，波動力達到14.5 N。

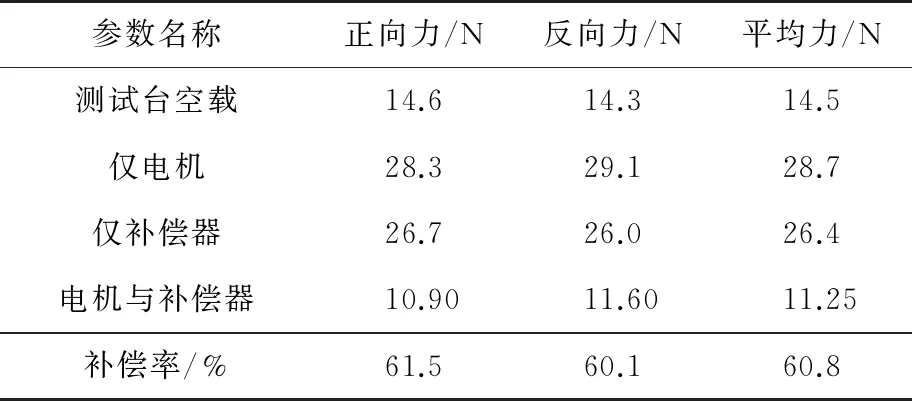
表3 電機與補償器磁阻力測試數(shù)據(jù)

圖9(b)所示為本文所述6槽8極電機磁阻力測試波形，顯而易見磁阻力主要諧波含量為2倍頻(τ=15 mm)，且磁阻力諧波的幅值為28.7 N，為仿真數(shù)據(jù)的83.7%(前述仿真數(shù)據(jù)為23.9 N)。其中正、反方向波形相位、幅值、頻率均基本保持一致，存在的偏置主要是由摩擦力造成的。圖9(c)所示為補償器磁阻力測試波形，其磁阻力波形與直線電機波形諧波含量相同，但相位相反。因此，補償器能夠實現(xiàn)直線電機磁阻力補償，且與理論分析結果一致。圖9(d)為本文所述補償器與直線電機相配合下的磁阻力測試波形，此時的磁阻力僅為11.8 N，補償器補償磁阻力效果達到60.8%(仿真為69.9%)，且合成磁阻力的2倍頻諧波已經基本消除。仿真數(shù)據(jù)與測試數(shù)據(jù)的差別主要在于前述分析的測試臺本身誤差以及有限元仿真剖分等綜合因素造成的。

圖9 6槽8極直線電機磁阻力測試波形

5 結 語

本文提出一種直線電機推力波動補償?shù)姆椒ā⒁鹬本€電機推力波動的力(本文稱之為磁阻力)分為兩種分量:(1) 由于直線電機初級鐵心的開斷而產生的力，稱之為邊端力；(2) 由于齒槽效應而產生的力，稱之為齒槽力。其次通過解析法，精確計算并歸納邊端力與齒槽力的一般規(guī)律，并合理設置補償器參數(shù)。然后，以一臺6槽8極電機為例，將解析結果與仿真結果相比較，并進行了試驗驗證。結果表明本文所述補償器能實現(xiàn)直線電機磁阻力補償，對直線電機推力波動具有較好的抑制效果。