基于系統微分響應的暴雨強度公式參數優化
李瓊芳,許樹洪,周正模,和鵬飛,杜 堯,虞美秀,陳啟慧
(1.河海大學水文水資源學院,江蘇 南京 210098;2.長江保護與綠色發展研究院,江蘇 南京 210098)
高精度的暴雨強度公式是城市防洪排澇基礎設施建設規劃設計的重要依據,事關城市地區人民生命財產安全和社會經濟的可持續發展[1]。在過去幾十年的探索與實踐中,已經形成了暴雨選樣、頻率分析、公式擬合的一套完善的暴雨公式編制流程。隨著新的優化算法的應用,公式參數的求解發展出多種方法[2-4],葉姍姍等[5]分別用粒子群算法、高斯-牛頓法、遺傳算法、麥夸爾特法推導得到淮安市暴雨強度公式,并對比分析了不同算法得到的結果;白慶芹等[6]選用麥夸爾特全局優化法、準牛頓全局優化法、模擬退火法、粒子群算法及遺傳算法求解得到暴雨強度公式參數;張小潭等[7]等基于改進的實時編碼加速遺傳算法(real coding-based accelerated genetic algorithm, RAGA)求解暴雨強度公式參數,并與傳統求解方法(牛頓迭代法、高斯-牛頓法)和優化算法(RAGA、蟻群算法)得到的結果進行了對比。盡管不同學者在求解暴雨強度公式參數時使用的優化方法有所不同,但在求解過程中均需要設定參數收斂的目標函數,如給殘差分配相等權重的絕對均方誤差、不等權重的相對均方誤差等,這類目標函數都與誤差平方和目標函數的本質相同。使用此類目標函數,一方面會由于非線性模型的參數平方而出現額外解[8];另一方面此類目標函數的響應面存在大量局部最優值,使智能算法很容易陷入局部最優,無法得到真正的全局最優解[9]。因此,智能算法求解非線性問題時會普遍出現參數等價性、模糊性、非唯一性、病態性和不可識別性現象[10],如暴雨強度公式參數求解中的“異參同效”問題[11]。針對以上問題,亟須論證智能算法求解暴雨強度公式參數能否收斂到全局最優[12],并探索在不考慮其他可行參數集的情況下能有效獲取唯一最優參數集[13]的新的暴雨強度公式參數求解方法。
本文以國家海綿城市建設試點城市——鎮江市為研究對象,解析暴雨強度公式參數求解常用目標函數響應面上參數解的空間分布特征,論證分析傳統智能算法在暴雨強度公式參數求解中的效果,提出基于系統微分響應的暴雨強度公式參數優化方法并分析其應用效果。研究成果可為優化求解暴雨強度公式參數和提升暴雨強度公式精度提供新的思路。
1 常用暴雨強度公式參數求解方法存在的問題
1.1 參數求解常用目標函數合理性分析
目前國內常用的4參數城市暴雨強度公式為
(1)
式中:I為暴雨強度;A1為雨力參數;C為校正參數;T為重現期;t為降雨歷時;b為修正參數;n為暴雨衰減指數。
《城市暴雨強度公式編制和設計暴雨雨型確定技術導則》(下文簡稱《導則》)中規定需要按編制公式計算暴雨強度并進行精度檢驗,不同于絕大多數非線性函數參數優化是以計算與實測樣本的誤差平方和為目標函數;GB 50014—2006《室外排水設計規范》(2011年版)(下文簡稱《規范》)則要求把計算值與實測值的平均絕對均方誤差(AMSE)和平均相對均方誤差(RMSE)作為評價暴雨強度公式精度的指標。因此,為使所得暴雨公式參數反映樣本統計特征,將AMSE或RMSE作為參數優選目標函數。
以一般p次非線性函數為例:
y=x+ax+(ax)2+…+(ax)p
(2)
式中:y為模型輸出;x為模型輸入;a為參數。
L個樣本的函數計算值與實測值的AMSE為
(3)
式中xi、yi分別為每組樣本的模型輸入和實測值。
將AMSE作為目標函數,對式(3)求一階偏導,得到
(4)
令上式等于0時會額外增加了p-1個參數解,因此將AMSE作為目標函數,求解此目標函數最小值時會顯著增加參數求解的不確定性。
假設暴雨強度公式參數值分別為A1=5、C=1、b=1、n=0.7,該暴雨強度公式可以表示為
(5)
以式(5)得到的暴雨強度為實測暴雨強度。假設存在4個樣本,分別為(T=10 a,t=5 min)、(T=10 a,t=6 min)、(T=100 a,t=5 min)、(T=100 a,t=6 min),并假定在參數C和b已知的條件下以AMSE為目標函數確定參數A1和n。假定A1在[0,10]內每間隔1取1個值,n在[0,1]內每間隔0.1取1個值,生成11×11的網格,計算網格點目標函數值,繪制得到網格化目標函數曲面,如圖1(a)所示,可以看到局部最優解沿深色區域呈曲線延展至全局最優,局部最優解共7個。
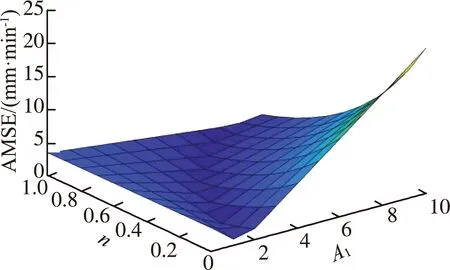
(a)2個未知參數
類似地,假定參數C已知,通過尋找AMSE最小的參數組合來確定未知參數A1、b、n。假定A1和b都在[0,10]內每間隔1取1個值,n在[0,1]內每間隔0.1取1個值,生成11×11×11的網格,計算網格點AMSE,得到的網格化目標函數曲面如圖1(b)所示,相應的局部最優解共21個。
隨著參數個數的增加和參數組合樣本的增多,目標函數曲面上的局部最優值數量越來越多,可以發現大量局部最優的目標函數值近似相同。因此可以推斷,當參數范圍越大,間隔步長越小(目標函數曲面越光滑),參數組合越多,局部最優參數解的個數會趨于無窮多個,并且在參數真值附近的局部最優解的目標函數值會與參數真值的目標函數值近似相等,“異參同效”現象非常顯著。
這些問題的存在表明暴雨強度公式參數求解常用的目標函數有缺陷,無法保證推求得到的參數解為真值。下面將結合具體案例進一步分析暴雨強度公式目標函數曲面上參數解的分布特征,并結合一些常用智能算法評價其求解能力。
1.2 基于具體案例的目標函數響應面參數解分布特征
1.2.1研究區選取及設計暴雨強度推求
選取國家海綿城市試點城市——鎮江市作為研究區。相關研究表明鎮江市短歷時暴雨發生次數呈顯著增長趨勢[14],因此編制高精度的城市暴雨強度公式對城市防洪至關重要。基于鎮江市國家基本氣象站丹徒站1981—2016年逐分鐘實測雨量資料,采用年最大值選樣方法構建5 min、10 min、15 min、20 min、30 min、45 min、60 min、90 min、120 min、150 min、180 min共11個歷時的暴雨資料統計樣本。考慮到P-Ⅲ型分布相較于耿貝爾分布和指數型分布更適用于研究區[15],選用P-Ⅲ型分布對各歷時年最大降水量樣本進行頻率分析,得到100 a、50 a、30 a、20 a、10 a、5 a、3 a、2 a共8個不同重現期不同歷時的設計暴雨強度(表1)。
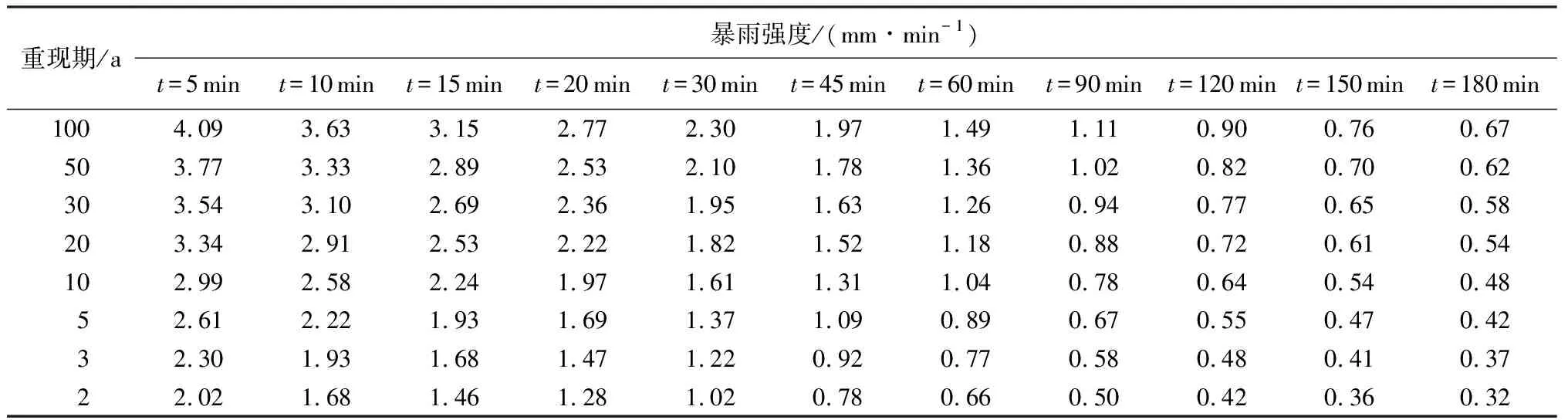
表1 不同歷時不同重現期的暴雨強度
1.2.2目標函數響應面參數解分布特征
由于樣本數量較大,目標函數較為復雜,很難通過對公式及目標函數的理論分析來獲取參數解數量和位置信息,因此采用隨機抽樣的方法分析參數解的信息。根據鎮江市暴雨強度公式現有的參數取值:A1=38.362 3、C=1.017 3、b=19.137 7和n=0.975,將各參數初始范圍設置為A1∈(0,50)、C∈(0,1.1)、b∈(0,30)、n∈(0,1),然后在參數范圍內通過均勻分布生成10萬組隨機樣本。根據《導則》要求編制的暴雨強度公式,其精度應滿足AMSE小于0.05 mm/min,RMSE小于5%,因此分別統計滿足精度要求的樣本組數,并確定相應的參數取值范圍,在此范圍內繼續進行抽樣,重復上述步驟直至滿足精度要求的參數范圍不再變化為止,最后點繪出該參數范圍內樣本參數值-目標函數值關系圖,并分析參數解的分布特征。
表2給出了均勻隨機抽樣結果。在沒有有效確定參數初始值范圍的情況下,10萬組樣本中僅有2組樣本滿足AMSE小于0.05 mm/min,即隨機抽樣法求解參數能滿足精度要求的概率僅為0.000 02。經過第一次抽樣,縮小了參數初始值范圍,在第二次采用隨機抽樣法時,滿足精度要求的概率則達到了0.108 69,有了明顯提升,但滿足精度要求的參數范圍與前一次抽樣確定的參數范圍基本相同,說明能滿足AMSE小于0.05 mm/min的穩定的參數范圍已基本確定。想要通過進一步約束參數范圍來獲得最優解,需要加強約束條件。序號3給出了在第2次抽樣確定的參數范圍內隨機抽樣,統計滿足AMSE小于0.045 mm/min和RMSE小于4%的樣本個數及參數范圍。可以看出滿足AMSE小于0.045 mm/min的樣本數為3 118,即滿足精度要求的概率為0.031 18,但也發現滿足精度要求的參數范圍較初始范圍沒有較明顯的變化。此外,案例還表明滿足AMSE精度要求的樣本均能滿足RMSE的精度要求,因此下文均以AMSE作為目標函數進行分析。

表2 均勻隨機抽樣結果
圖2為第3次抽樣獲得的10萬組樣本的AMSE與各參數的關系。從圖2可以看出,約束參數范圍后抽樣所得到的樣本中仍有一部分無法滿足AMSE的精度要求;但滿足精度要求的參數解數量眾多,且不同參數樣本的目標函數值近乎相同;同時滿足AMSE最小的樣本有無窮多個,“異參同效”特征非常明顯,進一步證實了第1.1節的結論。此外,未發現能夠決定目標函數最優解的參數,但相對而言,AMSE對參數A1、n較為敏感,其值的合理界定能夠有效過濾導致目標函數值相對較大的無用樣本。當A1∈(37,38)、n∈(0.94,0.95)時,AMSE變化區間明顯縮窄,由樣本信息可知,當A1=37.877 9、n=0.943 8時,AMSE最小,因此A1、n范圍的有效界定對模型參數的優化求解尤為重要。通過上述抽樣分析方法可以不斷縮小參數范圍,最終選取對應于樣本中目標函數最小的參數組合作為最優解,但此方法相對繁瑣,建議慎用。
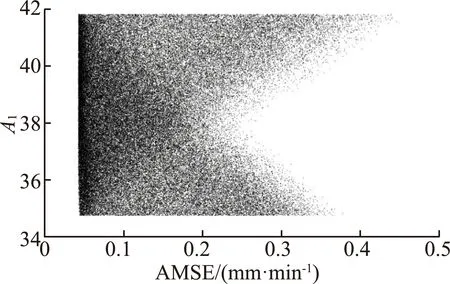
(a)A1-AMSE散點圖
從以上分析發現,在參數范圍未有效確定的情況下,滿足精度要求的有效樣本數目較少,而在縮小參數范圍后,滿足精度要求的參數解數量又較多,信息混雜。因此利用隨機搜索類優化算法推求暴雨強度公式參數無法保證所獲得的參數值是其真值。
在最終確定的參數范圍內生成多維度參數組合的離散化網格,并計算網格點目標函數值。將A1、C、b、n參數中任意兩個作為x和y軸,目標函數作為z軸,繪制參數-目標函數值三維空間圖(圖3);將A1、C、b、n參數中任意3個作為x、y和z軸,繪制參數-目標函數值切片圖(圖4)。基于三維空間圖和切片圖,分析參數變化對目標函數值的影響特征以及滿足精度要求的參數解數量及分布情況。
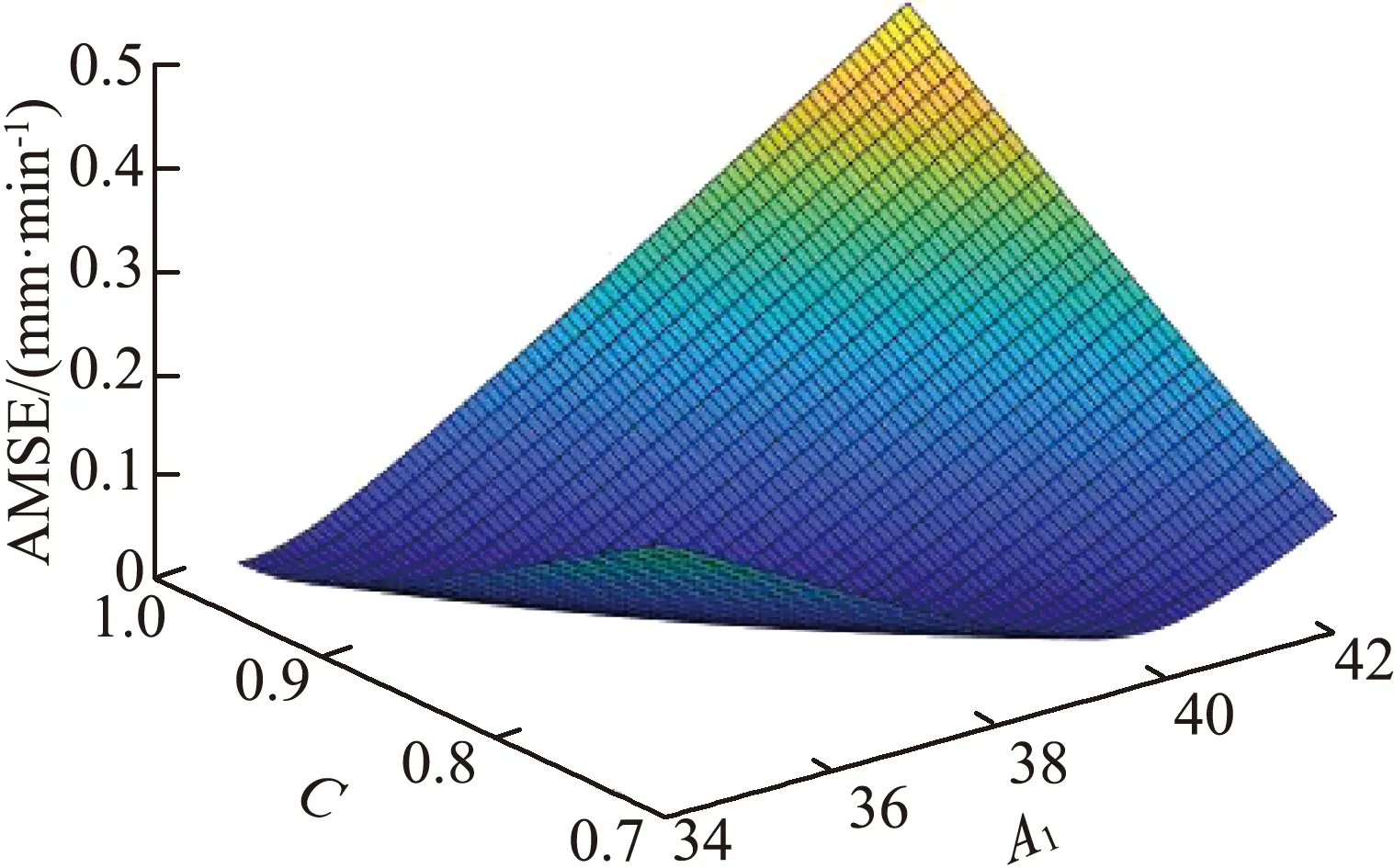
(a)A1、C
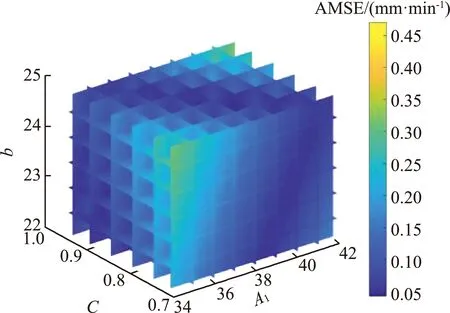
(a)A1、C、b
從圖3中可以看出,任意兩參數組合對應的目標函數響應面呈現U形,滿足精度要求的參數解分布在響應面底部深色區域,深色區域呈線性延展至全局最優點。響應面底部存在間隔分布的凹槽,凹槽底部為局部最優值。從圖4中可以看出,目標函數值較小的參數組合樣點分布在圖中深色區域,存在無窮多個,在參數變化范圍內均有分布。從其分布位置與參數的相互關系來看,A1、C、b參數中,目標函數值隨A1變化而變化,而基本不隨C、b變化而變化;A1、C、n參數中,參數A1、n對目標函數值影響程度大于參數C,尤其是當A1、n同時減小時,目標函數值也減小;A1、b、n參數中,A1、n對目標函數值影響程度大于參數b,目標函數值也是隨著A1、n的減小而減小,但不隨b變化而變化;C、b、n參數中,n對目標函數值的影響程度大于C、b,目標函數值隨著n的減小而減小,但不隨C、b變化而變化。總體來看,目標函數值對A1和n的敏感程度較高,此結論與采用Sobol法[16]的敏感性分析結果(表3)一致。
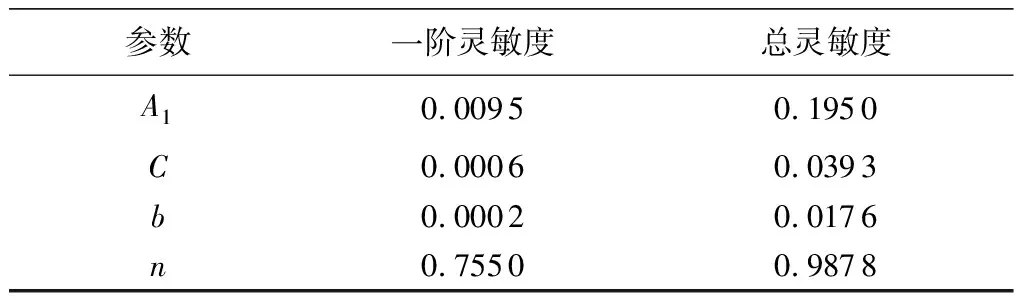
表3 Sobol法靈敏度分析結果
1.3 常用智能算法的暴雨強度公式參數求解能力
從以上分析結果來看,當采用隨機搜索的智能算法求解暴雨強度公式參數時存在以下問題:①在參數范圍沒有得到有效界定的情況下,基于隨機生成的參數個體/種群來篩選信息進而尋優,很難隨機生成包含全局最優參數信息的種群;②即使在參數范圍確定的情況下,由于局部最優值數量過多,當初始生成的參數種群不包含全局最優信息時,算法會陷入局部最優,避免陷入局部最優的辦法是增加新的參數樣本更新種群,但如果新的參數樣本仍然不能包含全局最優信息,算法又會陷入下一個局部最優;③由于全局最優附近的局部最優和全局最優的目標函數差別太小,而數學軟件能識別的小數位數有限,算法將局部最優等同于全局最優處理,最終得到的結果可能只是目標函數近似最小的局部最優參數解,即“異參同效”。
結合前面的實際案例,本文采用粒子群算法和SCE-UA(shuffled complex evolution algorithm)算法優化求解了鎮江市暴雨強度公式參數。表4給出了在參數初始范圍A1∈(0,50)、C∈(0,1)、b∈(0,30)和n∈(0,1)條件下兩種方法尋優得到的最終參數解及目標函數值。可以看出粒子群算法尋優效果相對較好,5次參數尋優對應的目標函數均滿足精度要求(<0.05 mm/min),但每次參數解卻不盡相同。需要指出的是,當目標函數最小值落在參數范圍邊界時,算法不能夠自動折返,而會陷入局部尋優。SCE-UA算法在求解具有區間約束的非線性問題時較為有效[17],但在參數范圍沒有得到有效約束的情況下,尋優效果相對較差。
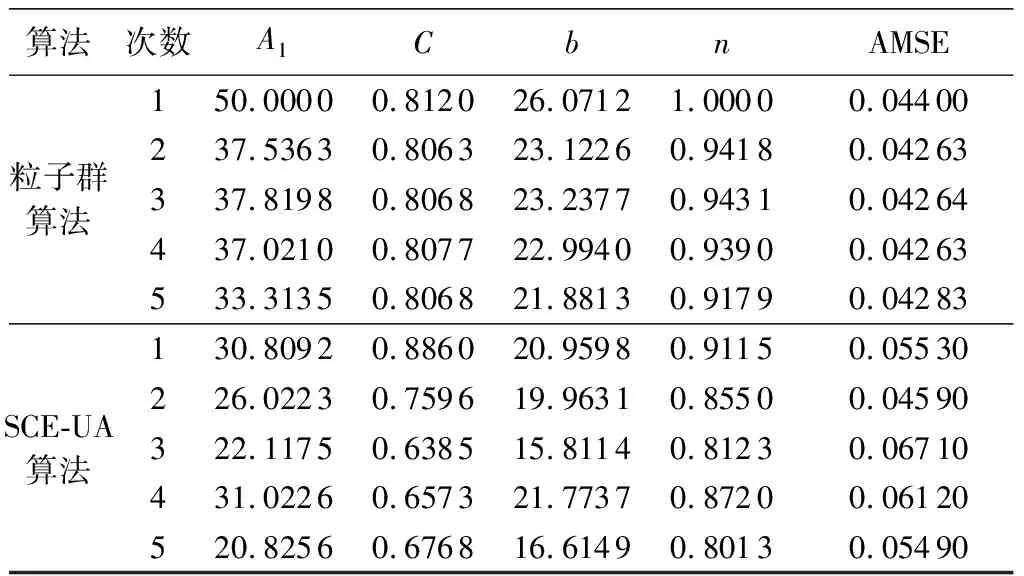
表4 優化算法參數解及目標函數值
2 暴雨強度公式參數系統微分響應求解方法
上述分析表明,以AMSE/RMSE為目標函數,在目標函數響應面上進行參數尋優存在諸多問題。由于暴雨強度公式本身在參數鄰域內連續且可求導,因此可通過樣本(Xi,Yi)與參數函數y(Y)=f(θ,Xi)相交的位置獲取參數真值信息,從而使得在參數函數曲面上尋優的系統微分響應方法[18]具有較大的應用價值。
假設非線性函數模型可以表示為
Y=f(θ,X)
(6)
其中
θ=(θ1,θ2,…,θq)T
X=(x1,x2,…,xk)T
式中:θ為模型參數;X為模型輸入自變量。
在模型參數優化時,將模型參數看作自變量,對函數模型線性化,即一階泰勒級數展開。其表達式為
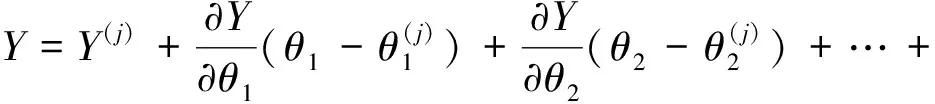
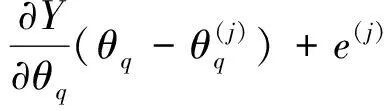
(7)
其中
Y(j)=f(θ(j),X)
式中:j為迭代次數;θ(j)為參數θ第j次率定值;e(j)為觀測值與計算值的偏差。
假定共有m組觀測樣本,即(X1,Y1)、(X2,Y2)、…、(Xm,Ym),函數模型向量形式為
Y=Y(j)+S(θ-θ(j))+E(j)
(8)
其中
Y=(Y1,Y2,…,Ym)T
要使函數計算值與觀測值誤差最小,校正后的參數θ滿足:
(9)
因此,式(8)變換為Y-Y(j)=S(θ-θ(j)),由此可得
θ(j+1)=θ(j)+(STS)-1ST(Y-Y(j))
(10)
通過上述過程可由初始參數值一步步迭代計算得到參數最優值。但是由于式(7)只是對實際函數的線性近似,忽略了高階泰勒級數展開項。因此引入校正系數c(c>1),將式(8)修正為
Y=Y(j)+cS(θ-θ(j))+E(j)
(11)
相應地,式(10)可變化為迭代式:
θ(j+1)=θ(j)+B(STS)-1ST(Y-Y(j))
(12)
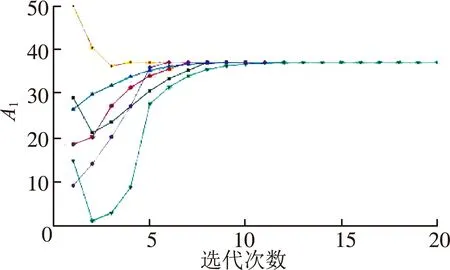
式中0 (13) 計算迭代過程中止應同時滿足兩個原則: a.函數收斂原則。當算法在一次或多次迭代中不能明顯改善目標函數值時,迭代過程停止,即|Y(j+1)-Y(j)|<ε,其中ε為收斂性控制常數,ε≥0。 基于系統微分響應優化方法的暴雨強度公式參數優化求解步驟為:①參數A1、C、b、n的初始化,即隨機生成一組參數初始值θ(0);②將初始參數θ(0)與樣本結合,計算靈敏度矩陣S以及每個樣本的Y-Y(0);③根據式(10)確定搜索方向,根據式(12)(13)確定參數B;④利用式(12)計算得到θ(1);⑤判斷是否滿足收斂性原則,若滿足則終止尋優,若不滿足則令θ(1)=θ(0)轉步驟②。 為進一步分析系統微分響應參數優化方法的應用效果,利用該方法推求鎮江市暴雨強度公式。圖5給出了按照第2節步驟進行參數優化求解的迭代收斂過程(不同顏色代表參數不同初始值的優化過程)。由圖5可知,對于不同參數初始值,最后都能收斂到同一結果,即參數真值,且各參數迭代次數均在15次以內,表明算法優化效率較高。當參數初始值接近參數范圍下邊界時,在優化求解過程中,參數取值逐漸增加,逐漸逼近參數真值,且算法能夠通過靈敏度矩陣自動縮小步長,逐漸收斂到真值;而當參數取值接近參數范圍上邊界時,經過尋優,參數取值會向下邊界逼近,直至小于參數真值,再逐漸增大向真值逼近。由此可知,該方法更擅長于從參數取值范圍下邊界逼近參數真值,但當參數取值靠近上邊界時,算法都能有效折返,可以避免陷入局部最優。 (a)A1優化過程 綜上,暴雨強度公式參數線性化優化方法能夠尋找到暴雨強度公式參數的真值,且迭代次數較少,效率較高,該算法不需要通過目標函數反推參數,且能夠解決參數范圍的確定對求解結果的影響問題,能夠避免陷入局部最優。推求的5~180 min鎮江市暴雨強度公式為 (14) 式(14)所得暴雨強度公式計算的AMSE為0.042 63 mm/min,RMSE為3.360 1%,精度均滿足《規范》要求。 系統微分響應法的理論基礎是系統對參數擾動的局部敏感性[19],該方法在優化求解效率和精度上明顯優于粒子群、SCE-UA算法。該方法通過一階泰勒級數展開將非線性模型轉化為線性模型,同時利用最小二乘法求解線性逆問題,由暴雨強度的計算誤差推求參數的估計誤差,并以此進行參數修正,具有較為清晰的物理解釋,結構較為簡單,性能較為穩定。針對暴雨強度公式參數求解中遇到的“異參同效”難題,許多優化算法可能僅僅得到了滿足精度要求的一種解,而非唯一解,而系統微分響應法可以高效獲得暴雨強度公式參數真值,表現出了明顯的優勢。從推導過程來看,該方法應適用于其他地區暴雨強度公式參數的優選求解。此外,如何構造新的目標函數來提高參數優化方法的優化性能[20],同時反映模型系統參數本身特性,這是參數優化領域的一大難題。在暴雨強度公式推求應用中,新目標函數的確定也具有研究價值,李增永等[21]在推求暴雨強度公式參數時,采用對數離差絕對值和平均對數離差絕對值作為目標函數,此目標函數反映出雙對數坐標系中暴雨強度-歷時關系曲線呈現階段式的線性特征[22],因此從理論上更能反映暴雨衰減指數隨歷時變化的特點,但此目標函數響應面的參數解數量、分布特征以及目標函數與參數的關系值得進一步研究論證。 a.常用的以RMSE或AMSE作為目標函數的暴雨強度公式參數優化方法存在局限性,增加了參數求解的不確定性,無法保證推求得到的參數解為真值。 b.基于隨機搜索的優化算法在優化求解暴雨強度公式參數時可能僅僅得到了局部最優值,而非全局最優。 c.基于系統微分響應的暴雨強度公式參數求解方法優化求解效率較高,且能獲得參數真值。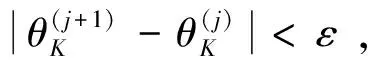
3 實例應用與討論
3.1 實例應用
3.2 討 論
4 結 論

