帶狀態(tài)依賴時滯微分方程的周期與幾乎周期解的應(yīng)用

周 輝, 王 文

(合肥師范學(xué)院數(shù)學(xué)與統(tǒng)計學(xué)院，合肥 230601)

0 引言

在過去四五十年，由于帶狀態(tài)依賴時滯的泛函微分方程常被用來描述許多模型動力學(xué)[1–2]，從而，此類系統(tǒng)引起了人們的研究興趣。關(guān)于帶狀態(tài)依賴時滯的泛函微分方程的研究在解的存在性[3]、可微性[4–5]、穩(wěn)定性[6]、同變性[7]以及可析性[8]等取得一些進(jìn)展。另一方面，早期關(guān)于此類方程的周期結(jié)果通常利用拓?fù)洳粍狱c定理與不定點指數(shù)方法得到的[9–11]。1974 年，Nussbaum[12]首次給出了依賴狀態(tài)時滯微分方程的周期解存在性結(jié)果。對于一般的周期解存在性問題的結(jié)果，可參考文獻(xiàn)[13]。2001 年，利用Mawhin 重合度定理并通過劃分區(qū)域估計解的一致上界，Li 與Kuang[14]獲得了如下方程的周期解

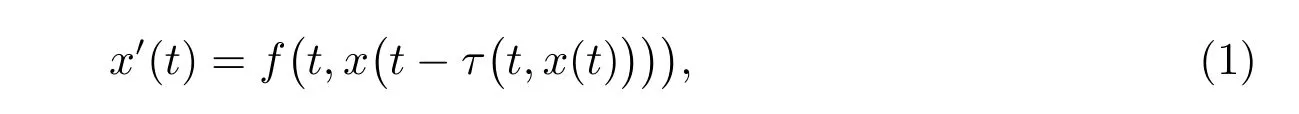
并給出自然且易驗證的周期解存在性判定條件。從此以后，這個方法經(jīng)常被用來處理時滯微分方程的周期解問題。另一方面，幾乎周期函數(shù)是周期函數(shù)的自然推廣[15–16]。時滯微分方程的幾乎周期解存在問題成為數(shù)學(xué)研究者關(guān)注的主題。眾所周知，帶依賴狀態(tài)時滯方程關(guān)于幾乎周期解的研究還很少。

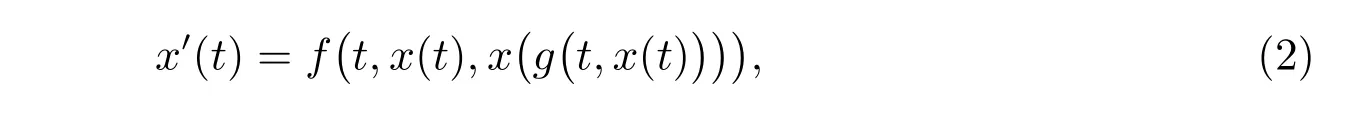
本文目的研究方程(1)的一般形式，即為其中x: R→Rn是未知函數(shù)，f與g在后文將具體給出。利用Schauder 不動點定理，本文分別給出方程(2)周期解與幾乎周期解的存在性條件，這些判據(jù)是較易于驗證的。同時，本文最后給出兩個例子說明所得理論結(jié)果的可行性。

1 主要結(jié)果

定理1假使f(t,x,y)與g(t,z)關(guān)于t均為T-周期的，且分別滿足Lipschitz 條件

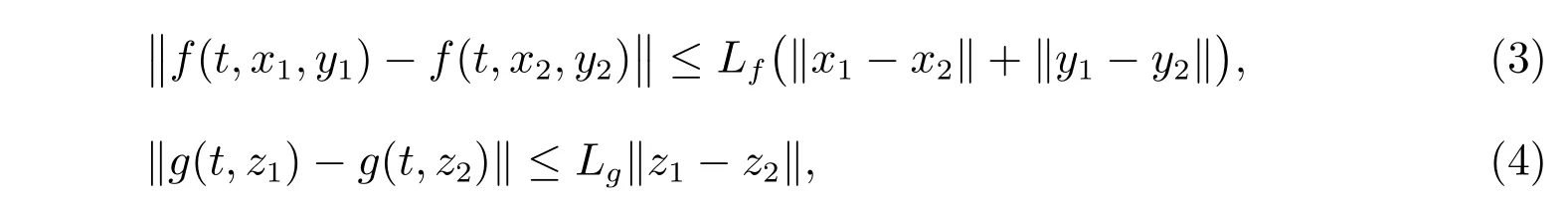
其中Lf、Lg是Lipschitz 常數(shù)，對任意的(x1,y1),(x2,y2)∈Rn×Rn和z1,z2∈Rn。關(guān)于T-周期函數(shù)x，如果f(t,x(t),x(g(t,x(t))))滿足

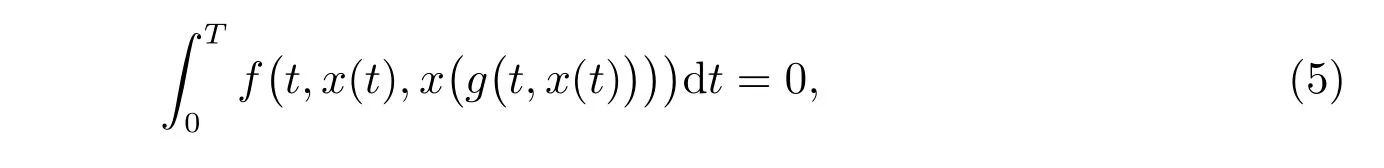
則方程(2)存在一個T-周期解。

證明 令X(T)為T-周期函數(shù)x:R→Rn的集合，它是賦予范數(shù)

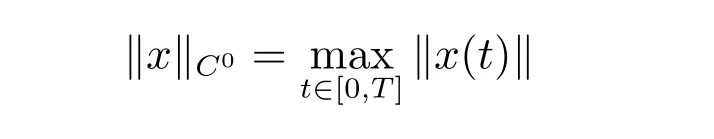
的Banach 空間。定義如下T-周期函數(shù)x構(gòu)成的有界集

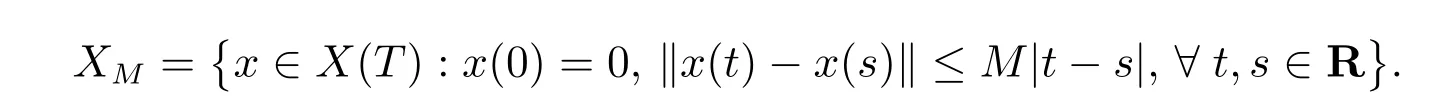
顯然，對x ∈XM，則有//x//C0≤MT。根據(jù)XM的定義，由于f(t,x,y)與g(t,z)分別滿足式(3)和式(4)，且它們關(guān)于t均為T-周期的。所以，對任意的x ∈XM，式(5)成立。

接下來，證明方程(2)的T-周期解屬于集合XM。定義映射G:XM →C0(R,Rn)為

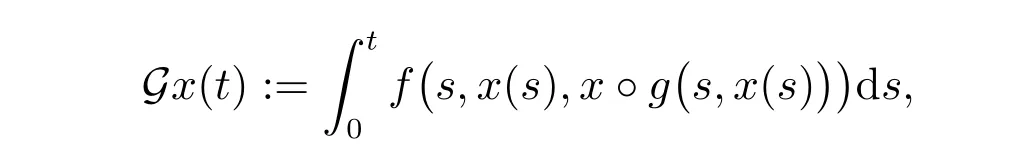
因此，G不動點是T-周期解，并有

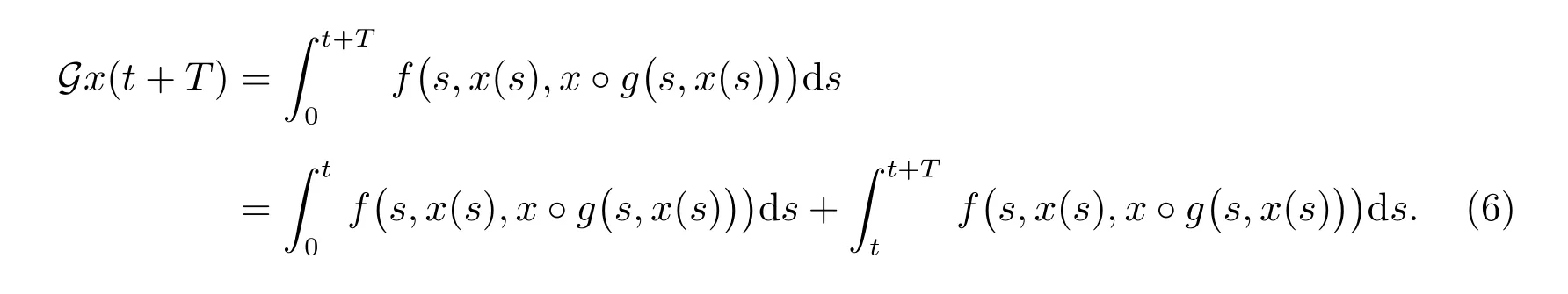
同時，利用式(6)，我們得到

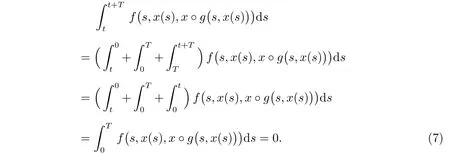
所以，由式(5)與式(7)，得到

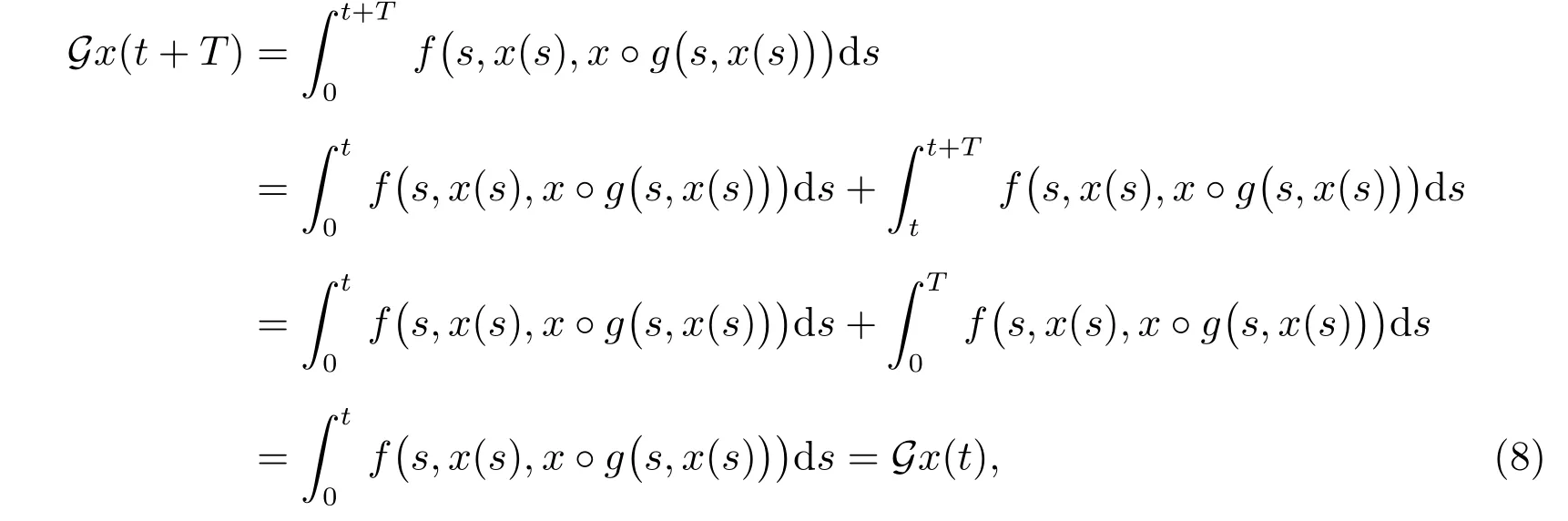
這就蘊含了Gx(t)∈X(T)。進(jìn)一步地

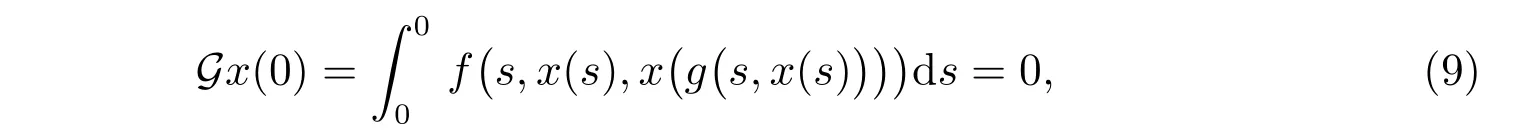
對任意的t,s ∈R，有

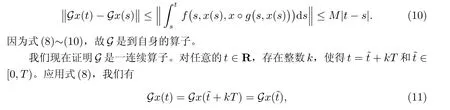
并且，對任意的s ∈R，有

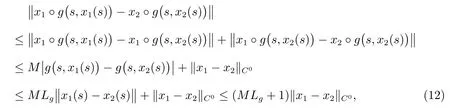
故式(11)和式(12)，可得

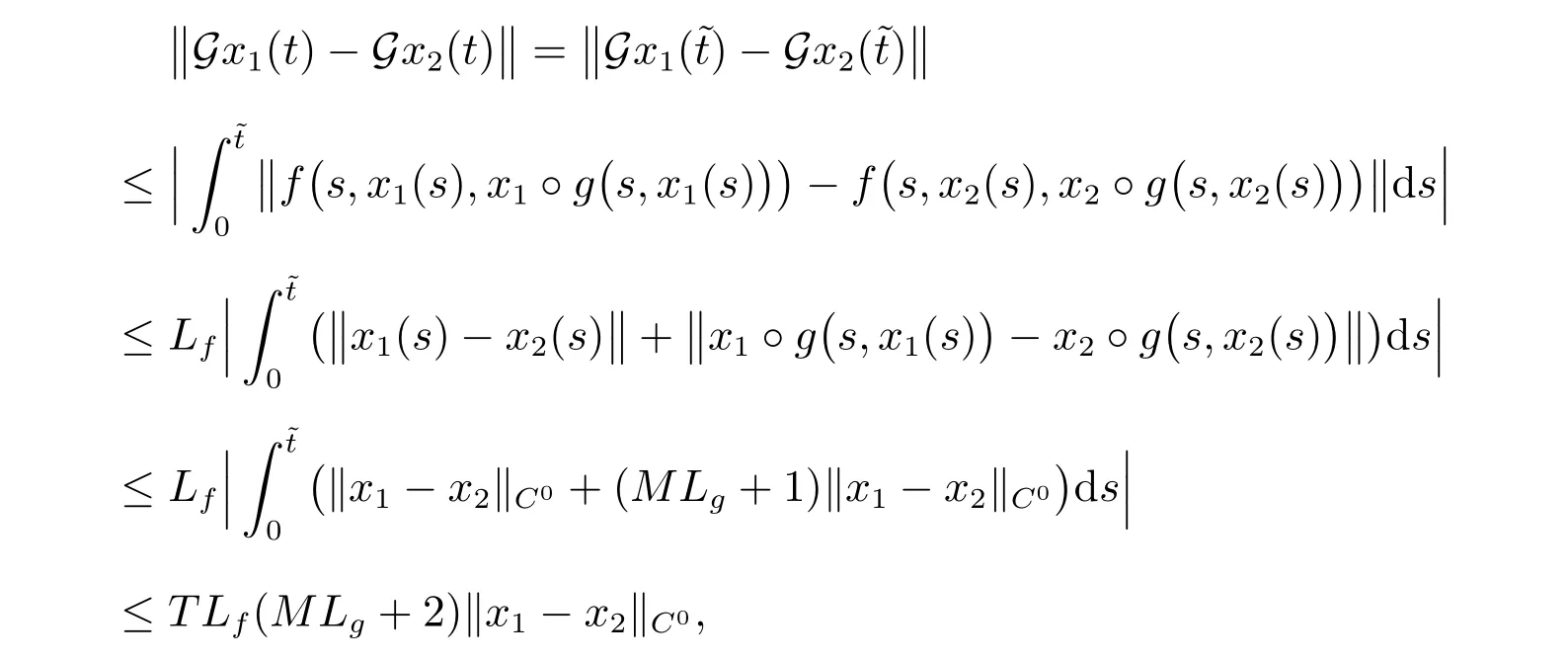
這就說明了G是連續(xù)的。

由于XM是Banach 空間X(T)凸且緊子集，而G又是連續(xù)的，根據(jù)Schauder 不動點定理，我們可得G在x ∈XM存在不定點，該不動點也即是方程(2)的T-周期解。

為了證明方程(2)存在幾乎周期解，我們首先給出一些基礎(chǔ)定義和預(yù)備引理[15,17]。

定義1函數(shù)f是幾乎周期的，是指若每個序列{α′n}存在一個子列{αn}，使得在R，式Tαf=limn→∞f(t+αn)一致成立。

令A(yù)P(R,Rn)代表從R 到Rn的幾乎周期函數(shù)的全體，則(AP(R,Rn),//·//)是Banach 空間[16]。

引理1[15]若x:R→Rn是幾乎周期的，則x(t)在R 上有界且一致連續(xù)的。

引理2[15]對x ∈Rn，若g:R×Rn →R 關(guān)于t是一致幾乎周期的，且?(t)?E是幾乎周期的，其中E是Rn的緊子集，則g(t,?(t))是幾乎周期的。

引理3假如x: R→Rn是幾乎周期的，g(t,x) : R×Rn →R 對x ∈H關(guān)于t是幾乎周期的，其中H為Rn的閉子集，則x ?(g(t,x(t)))是幾乎周期的。

證明 由引理1 與引理2，幾乎周期函數(shù)x(t)在R 上一致連續(xù)，且g(t,x(t))是幾乎周期的。再由定義1，存在實序列α={αn}，使得成立

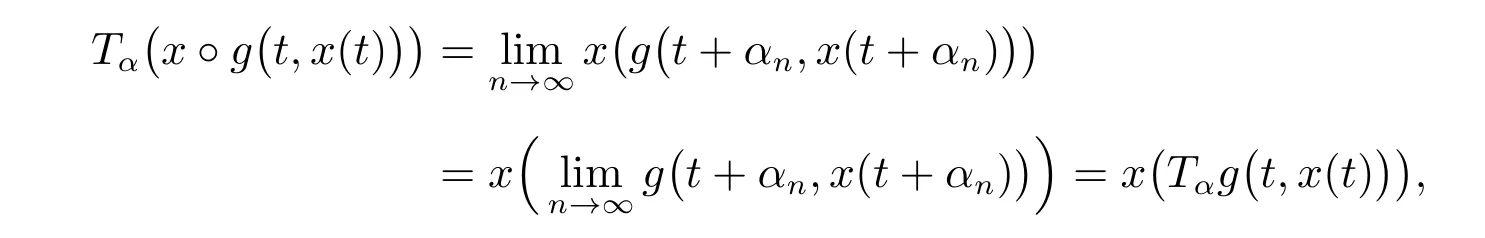
故x ?(g(t,x(t)))是幾乎周期的。

定理2若連續(xù)函數(shù)f(t,x,y)與g(t,z)關(guān)于t是幾乎周期的，且分別滿足Lipschitz 條件(3)和(4)。對幾乎周期函數(shù)x如果f(t,x(t),x(g(t,x(t))))是一致有界的，則方程(2)存在一個幾乎周期解。

證明 對幾乎周期函數(shù)x，令N為f的界函數(shù)全體，即為

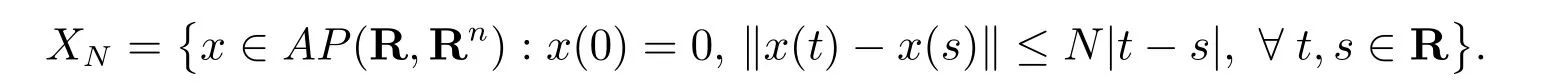
首先，證明方程(2)在集合XN中存在幾乎周期解。定義映射H:XN →C0(R,Rn)為

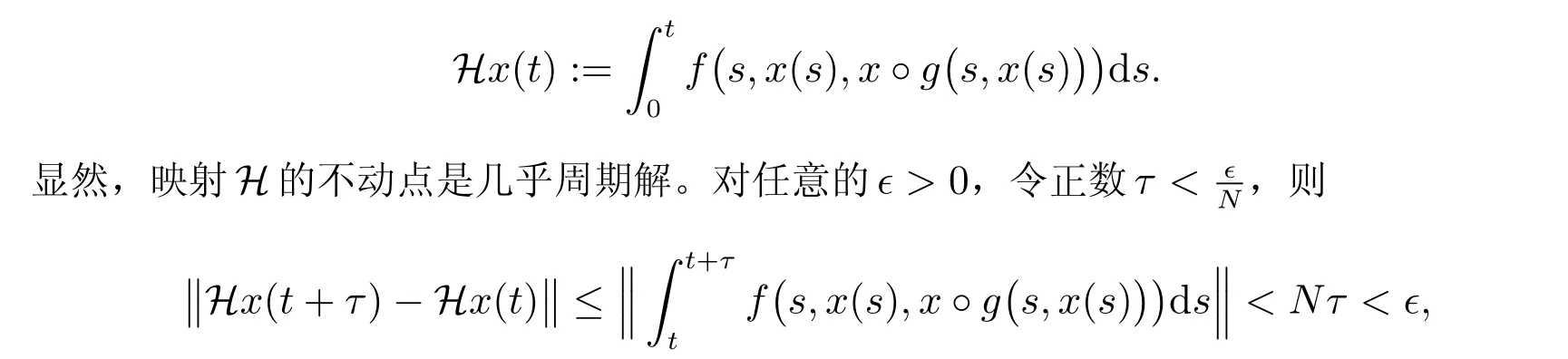
利用定理1 的證明方法，故有

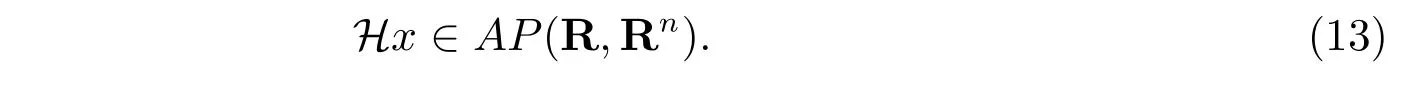
顯然有

對任意的t,s ∈R，可得

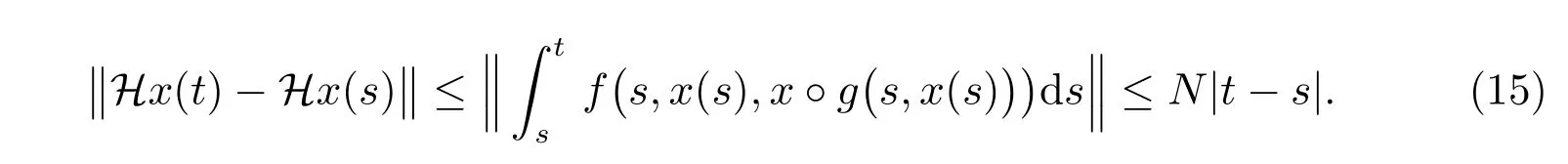
所以式(13)～(15)蘊含H是自身到自身的算子。

現(xiàn)在證明算子H是連續(xù)的。對任意的?>0 與xn(t)∈XN，它一致收斂于x(t)，存在正整數(shù)n1，當(dāng)n>n1時，有

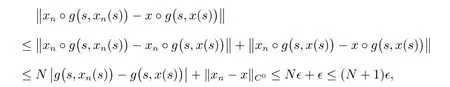
則

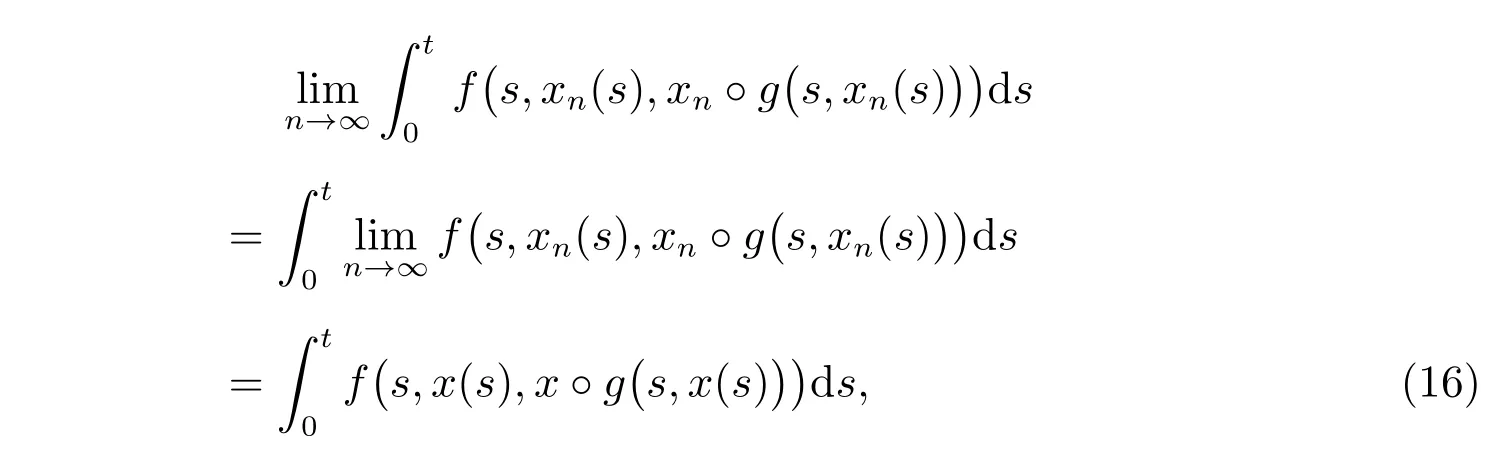
所以

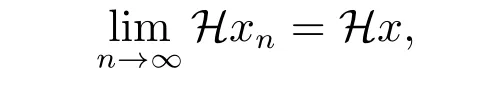
這說明了H的連續(xù)性.

由于XN是Banach 空間AP(R,Rn)上的凸緊子集，且H是連續(xù)算子，根據(jù)Schauder 不動點定理，映射H存在一個不動點h ∈XN，它即是方程(2)的一個幾乎周期解。

2 例子

本部分給出兩個例子，例證所得上述結(jié)果的可行性。

例1考慮如下依賴狀態(tài)時滯微分方程

由定理1，則方程(17)至少存在一個2π-周期x(t)解。

例2考慮如下泛函微分方程

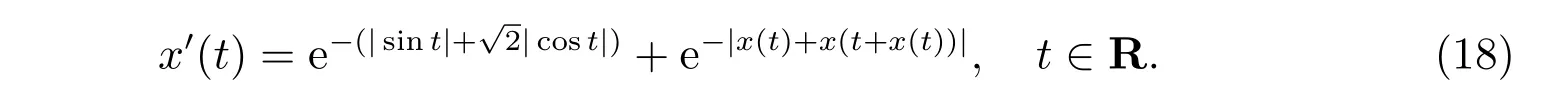
易得Lf,Lg＜1 與//f//C0≤2。根據(jù)定理2 及例1 可得，方程(18)存在一個幾乎周期解。

注1從上面兩個例子可以看出，本文的主要結(jié)果是可行的，可作為依賴狀態(tài)時滯微分方程存在周期解或幾乎周期解的判據(jù)，這些結(jié)果改進(jìn)了一些離散或分布時滯系統(tǒng)解的存在性結(jié)果。