船舶排放控制區政策對城市空氣質量影響的異質性分析

章強，陳萬響

(上海海事大學交通運輸學院，上海 201306)

0 引 言

隨著綠色航運理念的不斷深化，船舶大氣污染問題在全球范圍內受到了廣泛關注。為改善大氣環境質量，國際海事組織以及主要航運國家和地區紛紛采取措施控制船舶大氣污染物排放，其中設立船舶排放控制區(emission control area，ECA)是國內外控制船舶大氣污染物排放的典型政策手段。

我國于2015年12月出臺了《珠三角、長三角、環渤海(京津冀)水域船舶排放控制區實施方案》，設立了三大ECA對船舶污染物排放進行限制。在此基礎上，2018年底交通運輸部又發布了《船舶大氣污染物排放控制區實施方案》，對ECA政策實施范圍、實施標準等提出了新的要求。現有研究表明我國ECA政策的實施對于減少船舶大氣污染物排放具有明顯成效。然而，ECA政策在不同港口的實施效果表現出一定的異質性，只是現有關于ECA政策實施效果異質性的研究所涉及的港口數量相對較少，研究結論的普適性有待進一步論證。為深入、準確地評估ECA政策實施效果在不同地區所表現出的異質性，本文在現有研究的基礎上，擴大樣本數量，在綜合考量地理位置分布和數據可獲得性的基礎上，選取我國沿海28個港口城市作為研究對象，利用面板數據模型來探究ECA政策實施對不同港口城市空氣質量的影響程度。

1 國內外研究綜述

自2006年國際海事組織在波羅的海水域設立國際上首個ECA以來，ECA政策的實施效果及其有效性研究就受到學者們的關注。其中，“自下而上”和“自上而下”的船舶排放測算方法被廣泛采用。近年來越來越多的學者開始探索使用新的定量研究方法來評估ECA政策的實施效果。具體來看，相關的研究可分為兩大進路，一路側重于船舶排放實測數據的對比，另一路引入計量經濟學中的分析方法。

在基于實測數據的研究方面，SCHEMBARI等基于船上大氣污染監測站所采集的數據，以地中海地區的4個港口為研究對象，指出歐盟層面推出的船舶在港排放控制政策能夠有效降低港口大氣中的SO質量濃度，平均降幅可達66%。陳鴻展等使用“碳平衡法”，通過對ECA政策實施前后實船排放數據的對比研究，指出使用低硫燃油后船舶污染物排放會不同程度地下降，進而證實了ECA政策的有效性，但該研究選取的實測船舶的數量少且未包含多種船型。李亞芳等利用衛星數據進行反演計算，得到了渤海地區大氣中的SO質量濃度，通過分析比較實施ECA政策前后大氣中的SO質量濃度的時空分布，認為設立環渤海ECA對保護海洋環境具有積極作用。

在引入計量經濟學分析方法方面，WAN等采用雙重差分法，通過對實驗組和對照組的對比研究，證實了實施ECA政策能夠降低港口城市大氣中的SO質量濃度，還指出ECA政策的實施效果在不同地區具有一定的差異性。ZHANG等使用斷點回歸模型方法，研究了上海港實施ECA政策對上海市空氣質量的影響，其結果證明實行ECA政策有助于降低上海市大氣中日均SO質量濃度。章強等為探究ECA政策在我國不同港口實施的有效性，基于斷點回歸模型對ECA政策在上海港和天津港的實施效果進行了對比研究，結果表明實施ECA政策能有效降低港口城市大氣中的SO質量濃度，ECA政策在我國不同地區表現出較好的普適性。盡管上述研究深入分析了ECA政策的有效性，并就政策實施效果的異質性進行了初步研究，但所選取的研究對象較少，沿海港口覆蓋不足，對ECA政策實施效果的異質性研究還有待進一步加強。

就研究方法而言，面板數據是截面數據與時間序列數據的綜合，依托面板數據既可以分析個體之間的差異，又可以分析個體的動態變化特征。面板數據模型在很多研究領域有著廣泛的應用，其中也包括環境污染治理領域。例如，沙文兵等基于短面板數據，通過構建變截距固定效應模型研究了外商投資對工業廢氣排放的影響，結果顯示，外商的直接投資對我國的生態環境具有負面影響，且外商直接投資對東、中、西部三大區域生態環境的負面效應呈現出明顯的東高西低的梯度特征。金殿臣等采用面板數據固定效應模型探究了我國省級區域工業污染與工業增長的關系，指出我國大部分地區仍處于工業固體廢物生成量隨工業增長而不斷增加的階段。李婉紅等利用短面板數據，通過建立變截距固定效應模型研究了環境規制強度對污染密集行業綠色技術創新的影響，研究結果顯示，由于受經濟和企業特征等多方面因素影響，環境規制政策不會對所有污染密集型行業形成有效規制。現有文獻的研究成果充分表明，可以利用面板數據模型來研究評估ECA政策對城市空氣質量的影響。

2 面板數據模型的構建

2.1 變量的選取與說明

本文旨在探究ECA政策在我國不同港口城市實施效果的異質性。鑒于ECA政策的主要內容在于限制船用燃油的含硫量以減少船舶的硫氧化物排放，進而改善港口城市的空氣質量，為準確評估ECA政策對港口城市空氣質量的影響，選取港口城市年均SO質量濃度作為被解釋變量。核心解釋變量為ECA政策變量，將其設為虛擬變量，港口城市實施ECA政策前該虛擬變量取值為0，實施政策后則取值為1。考慮到港口城市大氣中的SO質量濃度除受船舶廢氣排放影響外，還主要受汽車尾氣排放以及城市工業生產過程中廢氣排放的影響，結合相關數據的可獲得性，本文將能夠反映到港船舶規模的港口貨物吞吐量、反映城市工業生產規模的第二產業產值占城市生產總值的比例和反映汽車尾氣排放規模的城市民用汽車保有量作為控制變量引入最終模型。

2.2 樣本選取與數據來源

選取2014—2019年我國28個沿海港口城市作為研究樣本，通過構建短面板數據模型展開研究。選取的這28個沿海港口城市遍布我國五大港口群，港口及城市規模具有明顯差異，有助于對ECA政策實施效果的異質性進行研究。各港口城市大氣中年均SO質量濃度數據來自各城市歷年《統計年鑒》和生態環境主管部門發布的年度數據，港口貨物吞吐量、城市第二產業產值占城市生產總值的比例和城市民用汽車保有量數據來自各城市歷年的《統計年鑒》，其中城市第二產業產值占城市生產總值的比例是通過采集到的第二產業產值和國民生產總值數據計算得出的。表1為相關變量的描述性統計結果。

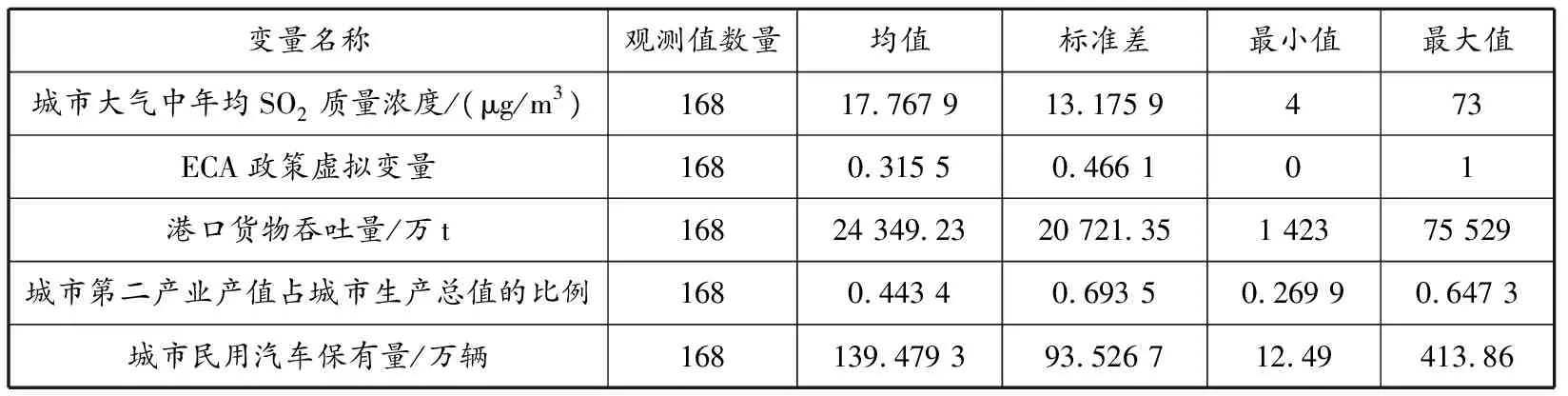
表1 相關變量的描述性統計

2.3 模型形式設定前的檢驗

根據有無個體影響和結構變化，面板數據模型可以分為無個體影響的不變系數模型、有個體影響的變截距模型和有個體影響的變系數模型3種形式，分別表示為

式中：為截面個體，=1,2,…,；為每個截面個體的觀測時期，=1,2,…,；為被解釋變量；和為截距項；為解釋變量；和為變量系數；為隨機誤差項。

為準確構建面板數據模型，首先需要明確是否存在個體影響。現假設==…=，==…=，若這個假設成立，則選用無個體影響的不變系數模型。本文利用Stata計量軟件進行個體效應檢驗得到，在1%顯著性水平上拒絕原假設，也即存在個體效應。由于個體效應可能以固定效應的形式存在，也可能以隨機效應的形式存在，故需要對其進行進一步明確。本文采用豪斯曼檢驗來檢驗個體影響與解釋變量之間的相關性，該檢驗的原假設為隨機效應模型中個體影響與解釋變量不相關。在該假設下，采用普通最小二乘法估計固定效應模型參數，采用廣義最小二乘法估計隨機效應模型參數，得到的估計參數都是無偏且一致的，不會有顯著的差異。基于此，建立豪斯曼檢驗統計量：

=(-)(-)

(4)

式中：和分別表示最小二乘虛擬變量法(least squares dummy variable, LSDV)和可行廣義最小二乘法(feasible generalized least squares, FGLS)所估計出的變量系數向量；表示經LSDV或FGLS估計后得到的協方差矩陣。經檢驗，拒絕原假設，需要選用固定效應模型。由于變化的截距僅能反映面板數據模型中忽略的反映個體差異的變量的影響，而不能體現反映經濟結構的相關解釋變量系數隨截面個體變化而產生的變化，所以需要進一步判別是選用固定影響變截距模型還是選用固定影響變系數模型。本文利用參數穩定性檢驗方法進行模型的最終選擇，該檢驗的原假設為==…=；經檢驗，拒絕原假設，故本文最終選用固定影響變系數模型。

2.4 模型的最終構建

經過上述一系列檢驗，選用固定影響變系數模型，具體形式為

=+1,+2,+3,+4,+

(5)

式中：=1,2,…,28分別代表28個港口城市；=1,2,…,6分別代表2014—2019年間不同的觀察年；表示經對數處理后的各港口城市大氣中年均SO質量濃度；1,表示各港口城市ECA政策虛擬變量，為虛擬變量的系數；2,、3,、4,分別表示經對數處理后的各港口城市的港口貨物吞吐量、第二產業產值占城市生產總值的比例和城市民用汽車保有量，、、分別為對應的變量系數；為擾動項；為截距項。

對式(5)進行系統估計所需估計的參數較多，從而導致自由度的損失。為減少所需估計的參數的數量，同時考慮到本文重點是ECA政策實施對港口城市空氣質量的影響，本文采用變系數模型中的部分變系數模型，即僅允許ECA政策虛擬變量系數依個體而變，而其余解釋變量的系數不依個體變化而變化。此時，需要利用LSDV進行模型估計，在回歸方程中引入個體虛擬變量以及個體虛擬變量與解釋變量1,的交互項。=1表示第個觀測個體，=0表示不是第個觀測個體。因此，本文最終設定的估計模型為

(6)

3 基于我國主要沿海港口城市面板數據的實證分析

3.1 面板數據回歸分析

利用Stata計量軟件對所構建的固定影響變系數模型進行估計，回歸模型可決系數達0.835 4，表明模型擬合度較好。得到的各港口城市的截距項和ECA政策虛擬變量系數估計結果見表2。由表2可以看出：ECA政策在大多數沿海港口城市均表現出良好的實施效果，即體現ECA政策減排能力的虛擬變量系數的估計值在一定的顯著性水平上為負數；ECA政策在不同港口城市的實施效果表現出明顯的異質性，例如，在鹽城該系數估計值為-1.09，而在汕頭該系數估計值僅為-0.001；廈門、秦皇島、唐山和中山這4個港口城市的政策虛擬變量系數估計值為負數，但不顯著；福州、東莞、珠海、湛江、北海這5個港口城市的政策虛擬變量系數估計值顯著為正數，反映出ECA政策未能發揮出其降低城市大氣中SO質量濃度的應有作用，對此將在后文進一步討論。

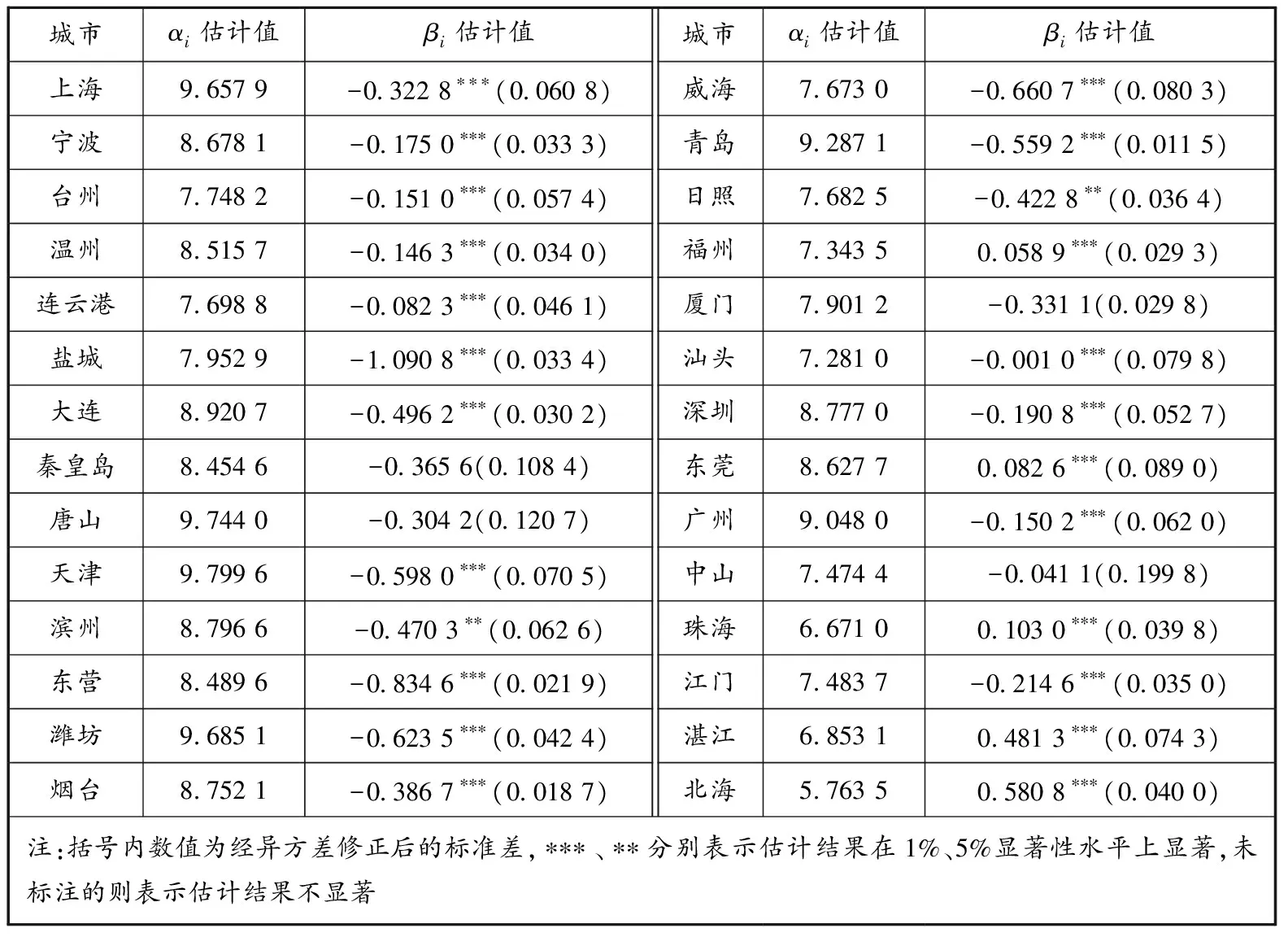
表2 固定影響變系數模型參數估計結果

3.2 回歸結果的穩健性檢驗

為確保實證研究結果的可靠性，需要對上述回歸結果開展穩健性檢驗。在使用面板數據模型的研究中，子樣本回歸法常被用來進行結果的穩健性檢驗。

由于到港船舶數量與港口貨物吞吐量密切相關，所以一般港口貨物吞吐量較少的港口城市受船舶排放污染的影響相對較小，這會使得ECA政策的實施對這類城市空氣質量的改善并不明顯，可能會影響研究的準確性。現從28個港口城市中剔除年均港口貨物吞吐量最少的5個港口城市濱州、威海、汕頭、中山和北海，對其余的23個港口城市進行回歸分析，得到的各港口城市的截距項和ECA政策虛擬變量系數估計結果見表3。由表3可以發現，政策虛擬變量系數顯著為負數、不顯著為負數和顯著為正數的港口城市分布與表2結果總體保持一致，說明原實證研究結果具有穩健性。

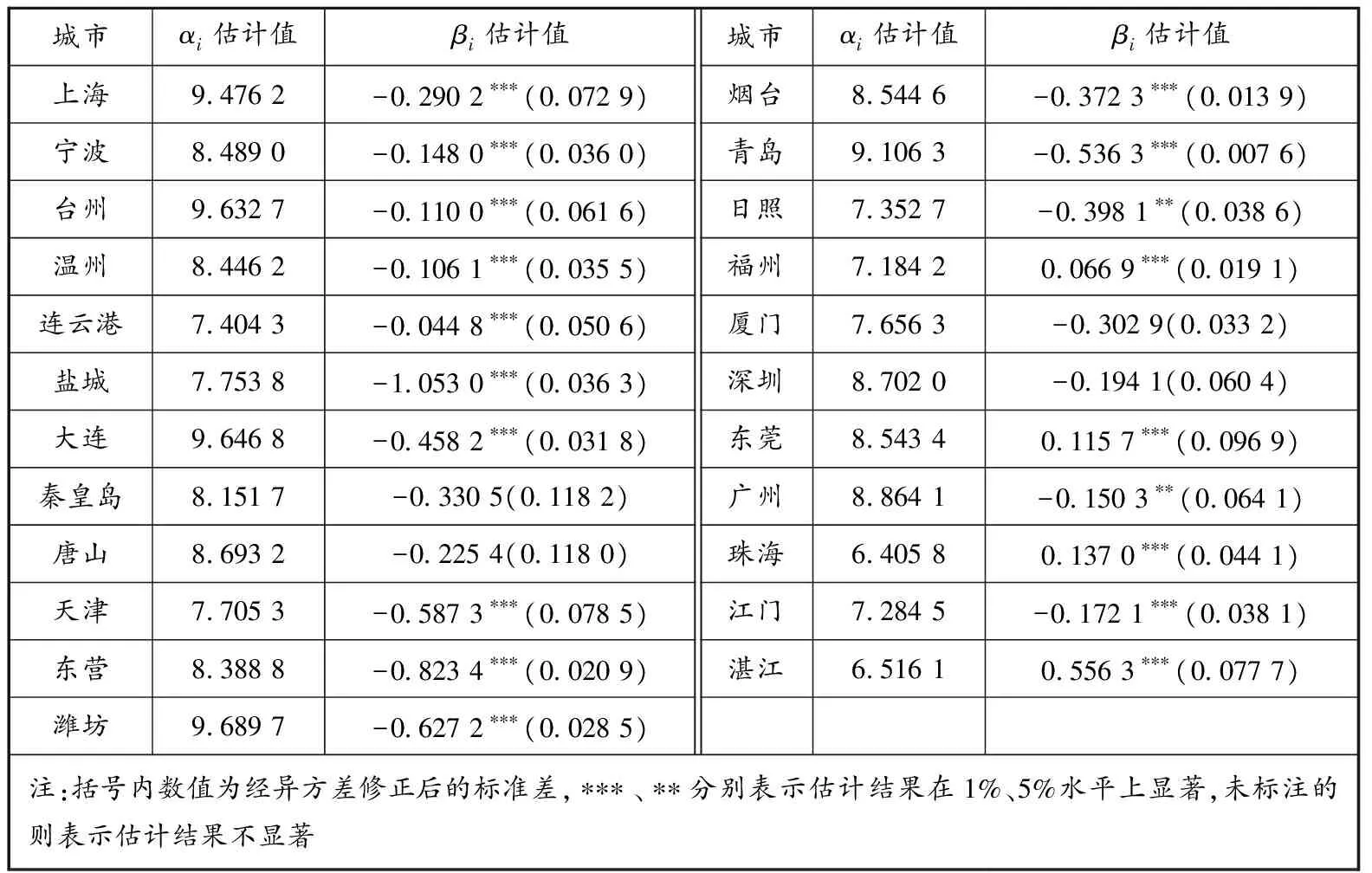
表3 減少樣本后的模型參數估計結果

4 針對實證結果的進一步闡釋

從表2不難發現，ECA政策的實施效果在我國沿海城市表現出較為明顯的地域差異。具體而言，ECA政策在環渤海地區的整體實施效果較為明顯，其中最為明顯的3個港口城市為東營、濰坊和天津，實施ECA政策后這3個港口城市大氣中的SO質量濃度分別降低了0.834 6%、0.623 5%、0.598 0%。ECA政策在長三角地區的整體實施效果也較好，但不及在環渤海地區的實施效果，以上海和寧波為例，實施ECA政策后這2個港口城市大氣中的SO質量濃度分別降低了0.290 2%和0.148 0%。相比環渤海地區和長三角地區，ECA政策在東南沿海、珠三角和西南沿海地區的實施效果表現出不穩定性，在部分港口城市表現出一定的減排成效，如深圳、廣州和江門市大氣中的SO質量濃度有一定程度的降低，但在部分港口城市如福州、珠海、北海則出現了統計意義上的不減反增現象。

除上述研究結果外，還要考慮到影響大氣中SO質量濃度的因素是復雜且多元的，包括氣候條件、社會經濟結構等。對于很多城市，特別是第二產業即工業較為發達的城市，非金屬礦物制品業、電力與熱力的生產和供應業、黑色金屬冶煉及壓延加工業等是城市大氣中SO的主要來源。近年來，我國沿海港口城市在實施ECA政策減少船舶排放的同時，也在不斷加大工業減排力度。相比而言，北方環渤海地區港口城市的第二產業產值占城市生產總值的比例較大，如上文提及的東營、濰坊和天津在2014—2019年間第二產業產值占城市生產總值比例的平均值分別為60.34%、42.70%、42.75%，因此這些港口城市的大氣污染物減排空間相對較大。在實施ECA政策前，東營、濰坊和天津市大氣中年均SO質量濃度分別為50.25、40.50、31.67 μg/m，而位于珠三角地區的江門、深圳、廣州市大氣中年均SO質量濃度分別僅為16.00、8.33、14.00 μg/m。

模型估計結果顯示，實施ECA政策使得大氣中SO質量濃度不減反增的港口城市有5個，分別為福州、東莞、珠海、湛江和北海，這些港口城市的一個共同特征是在實施ECA政策前空氣質量就長期保持良好水平。福州市空氣質量排名近10年來一直在全國名列前茅，在實施ECA政策前的2014—2018年間，其年均SO質量濃度僅為6.6 μg/m。西南沿海的湛江和北海在實施ECA政策前的2014—2018年間年均SO質量濃度分別為10.40、9.80 μg/m，均處于較低水平。處于珠三角地區的東莞和珠海于2017年就開始實施ECA政策，而在實施ECA政策前就采取了“騰籠換鳥”等措施，將高污染、高能耗的企業外遷，這些措施使得大氣污染物排放明顯減少，城市空氣質量顯著提高。上述港口城市出現的統計意義上的不減反增現象可能有兩個方面的原因，一是船舶廢氣排放在整個城市大氣污染物排放中占比較小，二是這些城市空氣質量整體上已保持在穩定的良好水平，ECA政策發揮成效的空間十分有限。

5 結 論

本文基于我國28個沿海港口城市的面板數據進行研究，結果顯示ECA政策在大多數沿海港口城市均表現出良好的實施效果，能夠起到降低大氣中SO質量濃度的作用，進而改善城市空氣質量，但ECA政策在不同地區的實施效果表現出一定的差異性。總體而言，在北方港口城市的減排效果整體上優于在南方港口城市的減排效果，這在很大程度上受氣候條件、社會經濟結構、現有空氣質量等多重因素的影響。

鑒于ECA政策在船舶廢氣減排方面的積極表現，我國應繼續堅持實施ECA政策，以2018年出臺的《船舶大氣污染物排放控制區實施方案》為基礎，繼續穩步推進現行ECA政策中關于硫氧化物和顆粒物排放控制要求的升級。針對ECA政策在不同地區的實施效果表現出的差異性，建議在未來ECA政策的實施過程中，采取分區域形式在不同地區實施具有一定差異化控制要求的ECA政策。