非線性彈性單盤轉子系統穩定性分析

劉繼華，茍學中，鄭龍席，高仁衡

(1.中國航發四川燃氣渦輪研究院，成都 610500；2.西北工業大學動力與能源學院，西安 710072)

1 引言

高轉速輕質結構是近代高速旋轉機械的設計趨勢，它提高了旋轉機械的性能，但也引發了很多嚴重的問題。尤其是線性理論得出的結果不僅誤差大，而且無法對實際出現過的自激振動、分岔現象、跳躍現象等做出解釋。動力機械工程中，具有強烈非線性的重要組成部分是油膜軸承的轉子系統，軸頸轉動產生的油膜壓力是非線性的。Shaw、Cveticanin對具有非線性彈性軸支撐的轉子系統進行了理論和試驗分析，表明此類系統存在混沌運動和振動突變現象。

穩定性是指系統受到微小擾動后保持原狀態的屬性，對于實際工況中的系統，其性能好壞都以系統穩定為前提。轉子-軸承系統的運動穩定性問題一直是轉子動力學研究的重要課題之一，國內外許多學者都在進行這方面的研究工作。劉繼華等基于有限差分法，對軸承-轉子系統進行穩定性分析，得出了臨界失穩轉速，結果表明適當增大偏心率能增加系統的穩定性。薛禹勝在電力系統穩定性分析中提出的互補群群際能量壁壘準則量化理論，在國內外若干電力系統中得到了成功的應用。Xue、李銀山等將應用于電力系統的運動穩定性量化理論的研究引入到非線性轉子系統。劉繼華等采用基于軌跡的加速度-位移擴展平面穩定裕度分析法，得出系統隨偏心量參數變化的穩定裕度變化情況。

判別轉子系統穩定性的方法較多，Poincare 映射圖是判斷穩定性的基礎。軸頸轉動產生的油膜力具有強烈的非線性，是影響系統穩定性的重要原因，這就需要對軸承間隙、潤滑油黏度等影響油膜壓力的因素進行分析。本文基于Capone 短軸承非線性油膜力模型，對轉子系統進行數值計算，采用Poincare映射方法得到轉子系統在偏心量、軸承間隙、潤滑油黏度3 個參數的特征圖，得出失穩轉速隨上述參數的變化規律。

2 數學模型

以圖1 所示的單盤對稱轉子為研究對象。圖中，兩端支撐為滑動短軸承，為軸瓦幾何中心，為軸頸中心，為轉子質心。采用目前廣泛應用的簡單離散轉子模型，將圖1中的轉子模型離散為3個質點，將軸段處的質量分別離散到軸頸和輪盤處，軸頸只考慮1/8 軸長的質量，軸只有、方向的平動和轉動共4 個自由度，約束軸向的平動和轉動自由度。單盤轉子系統的離散模型如圖2 所示，兩軸段等效為剛度，輪盤處的阻尼為，非線性油膜力分別作用在兩個軸頸處的質點上。

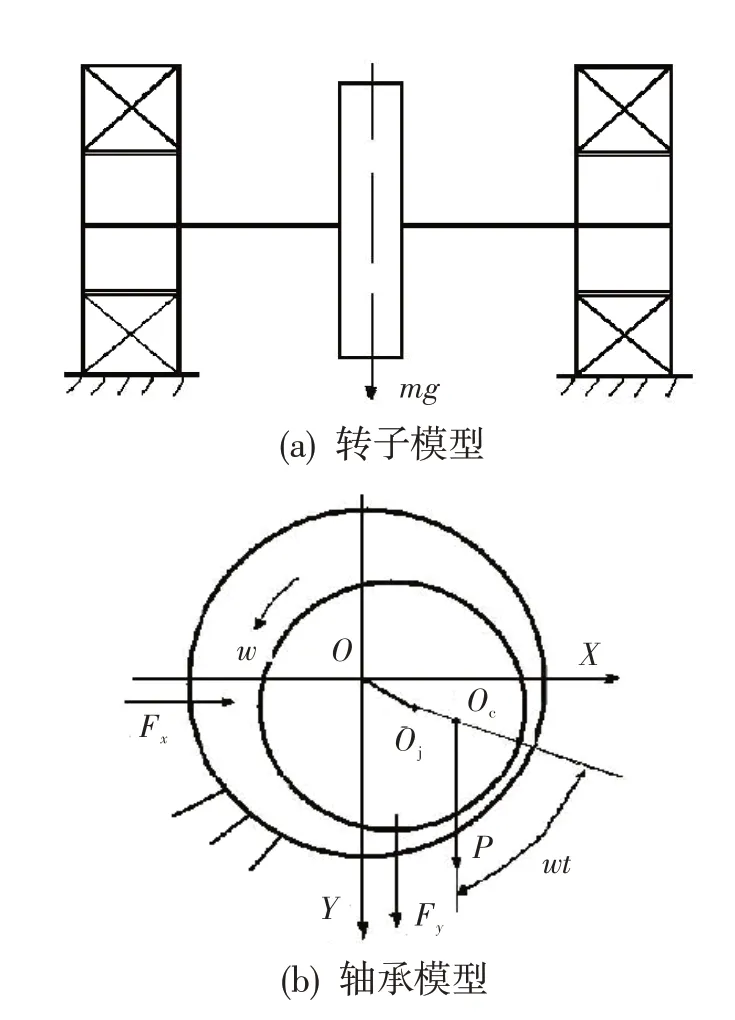
圖1 單盤對稱轉子動力學模型Fig.1 Single disk symmetric rotor model

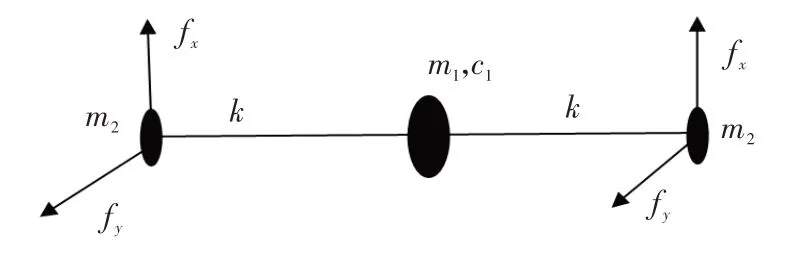
圖2 單盤轉子系統的離散模型Fig.2 Discrete model of a single disk rotor system

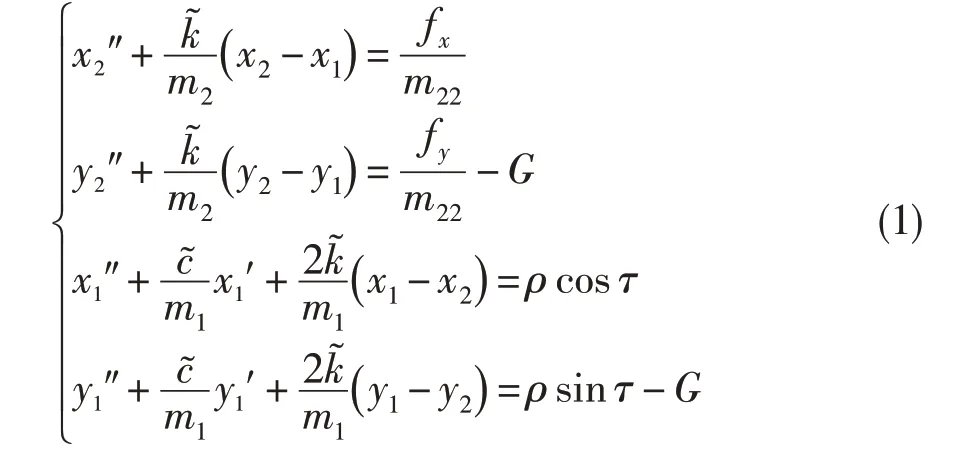
式中：f、f采用Capone 短軸承非線性油膜力模型，其詳細表達式見文獻[14]；=/()為轉子的無量綱重力；=/為無量綱質量，m為單盤處集中質量。

3 數值計算分析

式(1)描述了一個非線性動力學系統的微分耦合方程，可以由數值計算得出近似解。本文使用MATLAB 編程，由于油膜力和基座支撐力的強非線性作用，采用Rung-Kutta法求解。選用的時間步長為2π/100，誤差小于10，計算1 500 周期；為消除初值對瞬態響應的影響，去除系統前1 000周期響應數據。在進行系統穩定性分析時，轉子模型參數選取為：=420 kg，=50 kg，=28.5 mm，=0.2 mm，=57 mm，=0.018 Pa·s，=2.105×10，=3 000 N·s/m。

3.1 偏心量對轉子系統穩定性的影響

為研究轉軸和葉輪加工及安裝過程中的殘余偏心量對轉子系統穩定性的影響，首先需在固定偏心量(=0.20)下分析不同轉速(=300，430，500，650 rad/s)時的動態響應；然后得出固定偏心量(=0.20)的全局(=300～800 rad/s)分岔圖，尋找其分岔點；最后得出偏心量(=0.10～0.40)-轉速參數域分岔集。

由于系統在低轉速時均表現為工頻周期運動，本文只考慮轉速在300 rad/s及以上的運動。圖3為系統=0.20、=300 rad/s時的動態響應圖，可見系統表現為周期運動。圖4 為系統=0.20、=430 rad/s時的動態響應圖。可以看出，軸心軌跡為幾個相交的曲線，在Poincare 圖上表現為4 個離散的點；在頻譜圖上除工頻外，還出現了1/4、1/2、3/4 倍頻率，由此可以得出系統表現為4倍周期運動。這說明油膜失穩后，除了出現常見的半速渦動，還有渦動頻率為1/(=4，6，8…)的高階次諧波分量。圖5 為系統=0.20、=500 rad/s時的動態響應圖。可以看出，軸心軌跡為不相交的內凹封閉曲線，在Poincare 圖上表現為2 個離散的點；在頻譜圖上出現了1 個基頻和1個半頻，且半頻幅值比基頻幅值大；在時間歷程圖上表現為較規則的周期運動，出現了2個波峰，說明系統表現為倍周期運動。圖6 為系統=0.20、=650 rad/s 時的動態響應圖。可見，軸心軌跡表現為幾個相交的環形曲線，在Poincare 圖上表現為一些離散的點，但這些點并沒有形成一定的環形狀；在頻譜圖上出現了幾個可以約分的頻率，說明系統此時不是概周期運動，而是多倍周期運動。

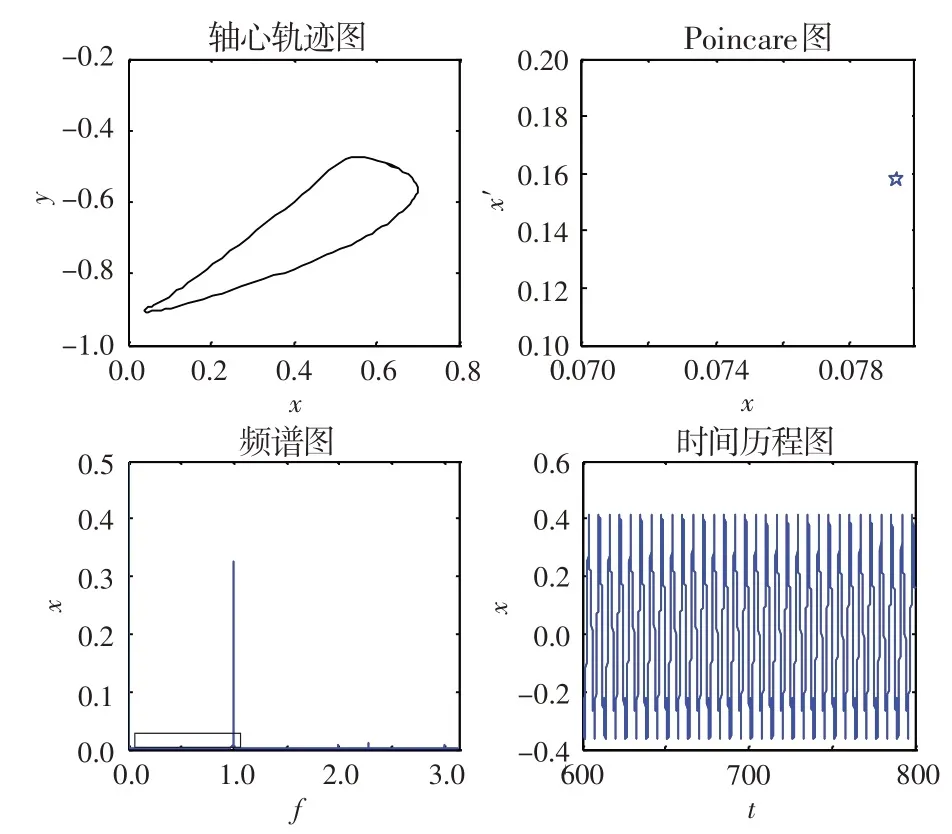
圖3 無量綱偏心量為0.20且轉速為300 rad/s時的動態響應圖Fig.3 Dynamic response diagram(ρ=0.20,w=300 rad/s)

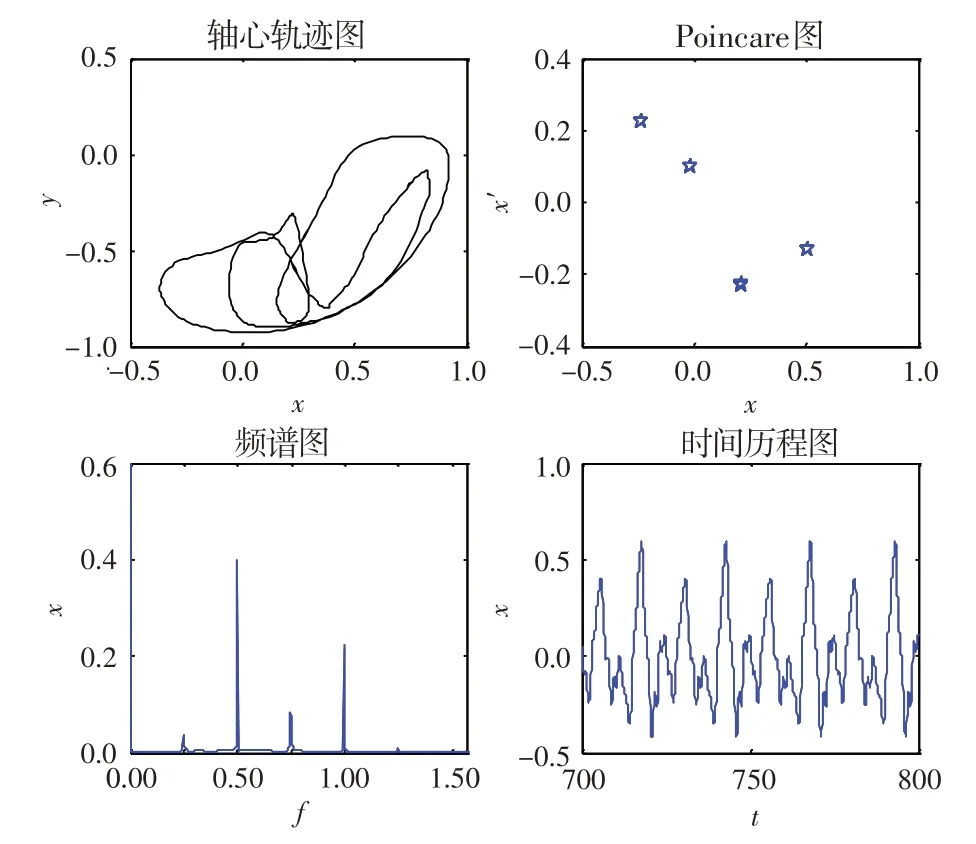
圖4 無量綱偏心量為0.20且轉速為430 rad/s時的動態響應圖Fig.4 Dynamic response diagram(ρ=0.20,w=430 rad/s)

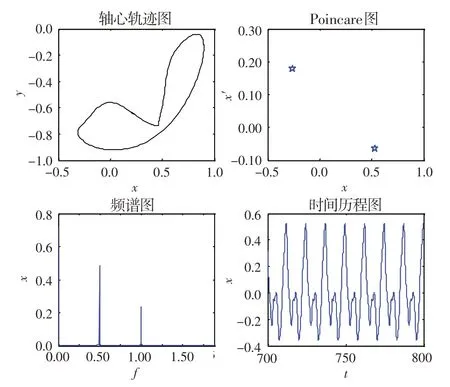
圖5 無量綱偏心量為0.20且轉速為500 rad/s時的動態響應圖Fig.5 Dynamic response diagram(ρ=0.20,w=500 rad/s)

圖6 無量綱偏心量為0.20且轉速為650 rad/s時的動態響應圖Fig.6 Dynamic response diagram(ρ=0.20,w=650 rad/s)

采用Poincare映射方法得出系統=0.20時的全局分岔圖，如圖7所示。可看出，轉速小于等于380 rad/s時，系統都表現為周期運動；轉速大于380 rad/s 時，系統的同頻周期運動發生分岔而失穩，系統表現為倍周期運動或多倍周期運動。

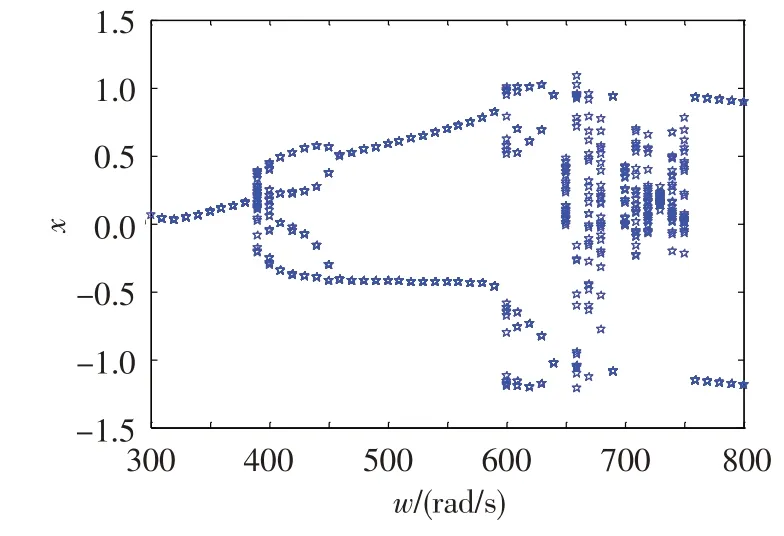
圖7 無量綱偏心量為0.20時的全局分岔圖Fig.7 Global bifurcation diagram(ρ=0.20)

由于轉子系統在不同偏心量時將出現不同的失穩特性，因此有必要研究偏心量對系統穩定性的影響。圖8 為轉子軸承系統在偏心量-轉速參數域內的分岔集。可以看出，無量綱偏心量小于0.25時，隨著偏心量增大，失穩轉速不斷降低，無量綱偏心量大于0.25時，隨著偏心量增大，失穩轉速又逐漸升高，系統存在著最低分岔失穩轉速。此轉速不僅和無量綱偏心量有關，而且還和其他因素有關系，系統運行時要特別注意避開。偏心量較小或較大都會增大系統的穩定性，但較大的不平衡力會引起轉子軸承受力增大，出現多倍周期運動以及有可能出現跳躍現象。所以為了系統安全運行，必須要對轉子進行較高精度的動平衡。本系統平衡后的無量綱偏心量至少要小于0.25。

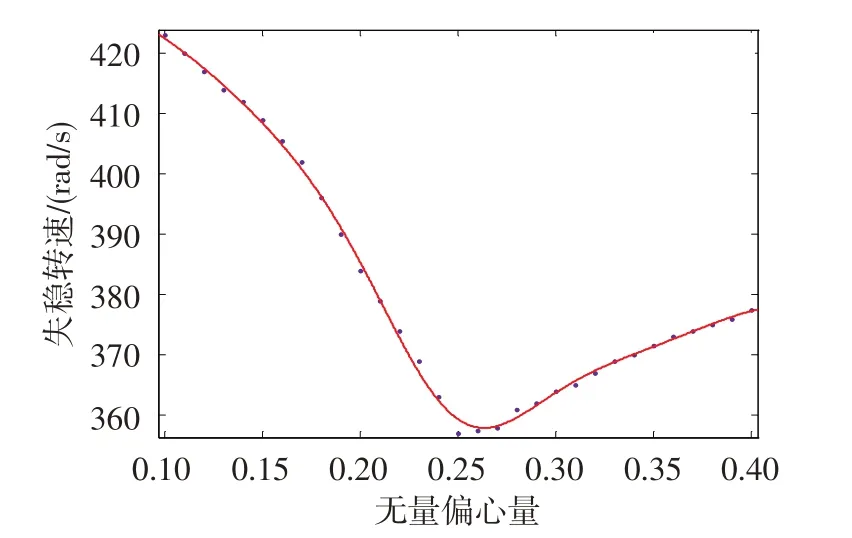
圖8 轉子軸承系統在偏心量-轉速參數域內的分岔集Fig.8 Bifurcation set of rotor bearing system with the parameter domain of eccentricity and speed

3.2 潤滑油動力黏度對轉子系統穩定性的影響

按照3.1節分析方法，對轉子系統無量綱偏心量分別為0.10、0.20、0.30、0.40時的不同潤滑動力黏度對系統穩定性的影響進行研究。圖9示出了轉子軸承系統油膜黏度-轉速參數域分岔集。可見，油膜黏度在0.015～0.050 Pa·s 區間，失穩轉速都是隨著油膜黏度的增加而增加。因此，為了提高系統穩定性和安全性，滑動軸承-轉子系統運行時，應選擇黏度較大的潤滑油。圖10 為國內航空發動機常用的某潤滑油的黏度-溫度曲線。可看出，隨著溫度降低，潤滑油黏度增大。為提高失穩轉速，需要對潤滑油進行冷卻，降低其溫度；但潤滑油黏度增大又會增加發動機阻力，導致發動機加速時間增大。因此，潤滑油黏度需要綜合考慮失穩轉速和發動機加速性。

圖9 轉子系統油膜黏度-轉速參數域分岔集Fig.9 Bifurcation set of oil film viscosity-speed parameter domain of rotor system

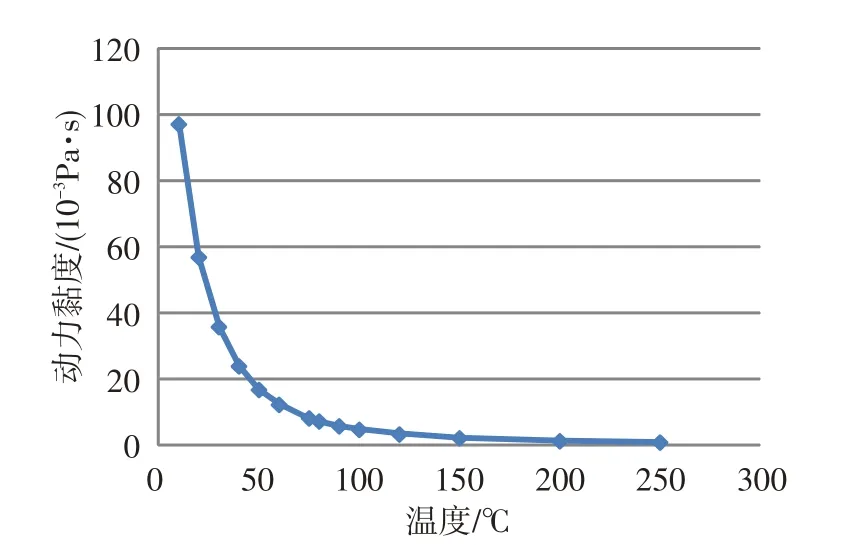
圖10 某潤滑油的動力黏度-溫度曲線Fig.10 Dynamic viscosity and temperature curve of a lubricating oil

表1給出了采用一次函數直線擬合得出的分岔失穩轉速與潤滑油黏度的關系。可以看出，隨著無量綱偏心量的增加，分岔失穩轉速隨潤滑油黏度的增加趨勢是先逐漸增大后逐漸減小。從圖9可以看出，雖然無量綱偏心量為0.10 時隨潤滑油黏度的增長趨勢較小，但分岔失穩轉速始終大于其他無量綱偏心量的。這再次說明，系統運行時，為了增加穩定性，應該對其進行較高精度的動平衡。比較無量綱偏心量為0.30 和0.40 時的分岔失穩轉速，黏度較小時無量綱偏心量0.30時的分岔失穩轉速大于無量綱偏心量0.40 的，但隨著黏度的增大，無量綱偏心量0.30 的分岔失穩轉速，逐漸小于無量綱偏心量0.40的。這說明系統的最低失穩轉速隨黏度變化。

表1 分岔失穩轉速與潤滑油黏度的關系Table1 The variation trend of bifurcation instability speed with the viscosity of lubricating oil

3.3 軸承間隙對轉子系統穩定性的影響

軸承結構直接影響著軸承-轉子系統的動態響應，軸承間隙是其中一個重要的參數。為研究軸承間隙對轉子系統穩定性的影響，首先需在固定偏心量(=0.02 mm)和軸承間隙(=0.25 mm)下，分析不同轉速的動態響應；然后得出固定軸承間隙(=0.25 mm)的全局(=300～800 rad/s)分岔圖，尋找其分岔點；最后得出軸承間隙(=0.20～0.30 mm)-轉速參數域分岔集。

圖11為=660 rad/s時的系統響應圖。可見，軸心軌跡為3個圓環，在Poincare圖上出現了3個離散點；在頻譜圖上除工頻外，還出現了1/3、2/3倍頻，說明此時為3倍周期運動。顯然，周期3不可能來自倍周期分岔，混沌學指出，周期3 意味著混沌，這種混沌叫做間隙混沌(陣發混沌)。

圖11 軸承間隙為0.25 mm且轉速為660 rad/s時的動態響應圖Fig.11 Dynamic response diagram(c=0.25 mm,w=660 rad/s)

采用Poincare映射方法得出系統在軸承間隙為0.25 mm 時的全局分岔圖，見圖12。根據圖12 以及上述分析可以得出，在轉速低于380 rad/s時，系統表現為工頻周期運動；轉速超過380 rad/s時，系統的同頻周期運動發生分岔而失穩；轉速在380～490 rad/s區間時，系統響應表現為倍周期運動；轉速在490～540 rad/s區間時，系統響應表現為周期運動；轉速在540～650 rad/s 區間時，系統響應表現為概周期運動；轉速在650～670 rad/s 區間時，系統響應表現為3 倍周期運動；轉速在670～800 rad/s 區間時，系統相應表現為從概周期運動逐漸變成周期運動。

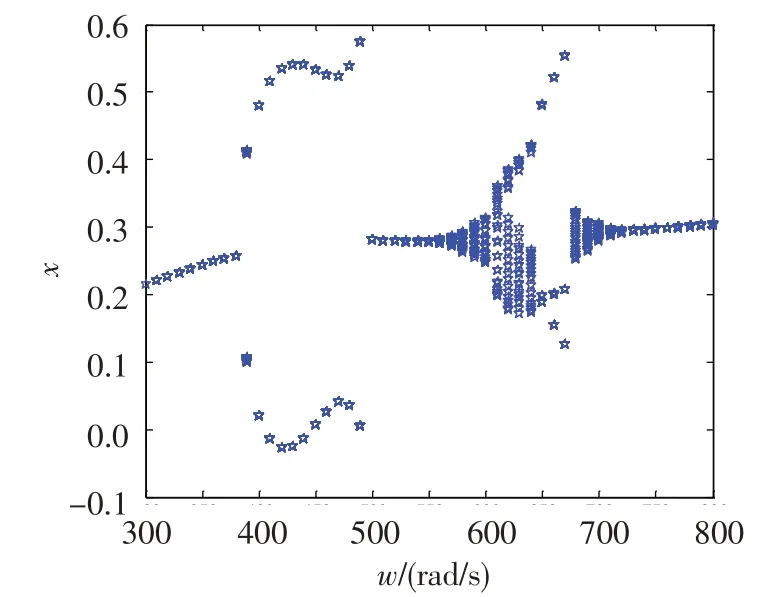
圖12 軸承間隙為0.25 mm時的全局分岔圖Fig.12 Global bifurcation diagram(c=0.25 mm)

圖13給出了軸承間隙從0.20 mm增加至0.30 mm時，轉子軸承系統在軸承間隙-轉速參數域內的分岔集。可以看出，隨著軸承間隙的增大，系統表現為倍周期分岔，分岔失穩轉速不斷降低。因此，在此類轉子-軸承系統設計中，應該選擇較小的軸承間隙。

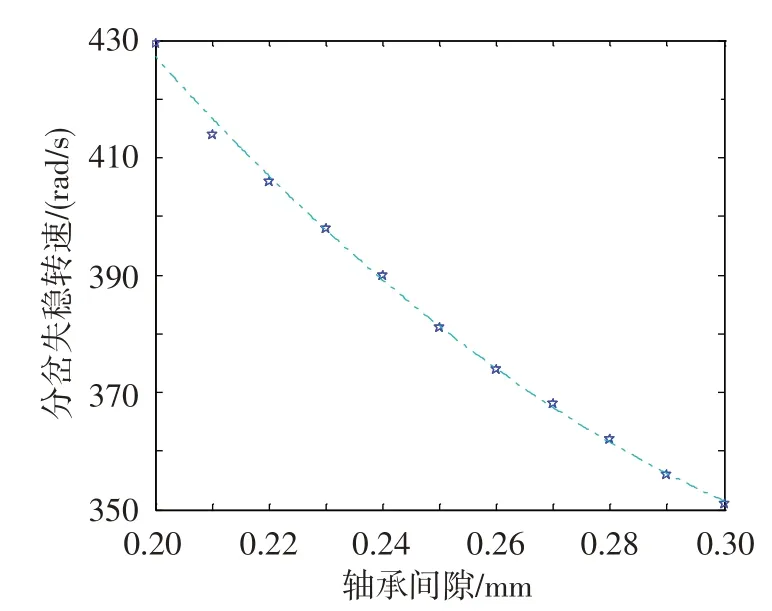
圖13 轉子軸承系統在軸承間隙-轉速參數域內的分岔集Fig.13 Bifurcation set of bearing clearance-speed in the parameter domain of rotor system

4 結論

采用Poincare 映射方法得到轉子系統的分岔圖、軸心軌跡圖、Poincare圖、時間歷程圖和頻譜圖，從而得出分岔失穩轉速隨偏心量、軸承間隙、潤滑油黏度3 個參數的變化規律。隨著偏心量的增大，分岔失穩轉速先減小后增大，存在最低分岔失穩轉速；隨著潤滑油黏度的增大，系統的分岔失穩轉速越來越高，穩定性越來越好；隨著軸承間隙的增大，分岔失穩轉速越來越低。滑動軸承-轉子系統設計和運行時，應盡可能選擇較小的軸承間隙和較大的潤滑油黏度，并進行較高精度的動平衡，以提高系統的穩定性和安全性。