基于改進GRU的電力大數據分析
張明達,崔昊楊,余豪華,孫益輝,王思謹,王浩乾
(1.國網浙江奉化區供電有限公司,浙江 奉化 315500;2.上海電力大學,上海 200090)
從數據的角度揭示電力設備內部狀態變化規律,是捕捉故障先兆信息、追溯故障過程、預測故障概率的重要依據。然而,電力設備狀態數據不僅來源多,還會由狀態監測系統可靠性差、測量失誤、設備系統擾動等情況導致不完整、冗余、遺漏、錯誤等無效異常數據的存在。這些無效、異常數據的出現導致設備狀態真實規律難以挖掘,嚴重者可能導致狀態規律挖掘錯誤。因此,如何避免無效異常值對設備真實規律挖掘的影響,以及如何提高數據挖掘算法的魯棒性成了電力大數據的核心問題。
目前,電力大數據分析常采用的方法按應用場景可分為:以整合移動平均自回歸模型(Autoregressive Integrated Moving Average model,ARIMA)為代表的統計分析,以神經網絡(Back Propagation,BP)、支持向量機(Support Vector Machine, SVM)等為代表的智能學習方法,以及以長短期記憶網絡(Long Short-Term Memory,LSTM)、門控循環單元(Gated Recurrent Unit,GRU)等為代表的深度智能學習方法。其中,以ARIMA為代表的統計分析方法不需大量樣本進行訓練,并且具有較高的準確率,但是當數據增大到一定規模后,該類算法容易陷入局部最優(即只反映短期規律,不能反映長期規律);以BP、SVM為代表的智能學習方法雖然容易訓練,但是海量數據處理時存在梯度消失的情況;而以LSTM、GRU等為代表的深度智能學習方法,由于具備長期的“記憶細胞”,可以輕松處理海量數據,并且具有極高的準確率,但是這類方法對數據的有效性、一致性、完整性的要求嚴苛。由于監測系統產生的無效異常值將破壞LSTM、GRU這類算法的“記憶細胞”,進而導致規律挖掘出錯或無法挖掘。
針對當前狀態數據存在的問題和現有GRU算法的不足,提出了基于改進GRU的電力大數據分析模型。該模型首先針對狀態數據一致性、有效性較差,以及沖擊、無效數據影響數據真實性的問題,利用自適應閾值的小波變換對數據進行清洗;其次,以周期為單位將清洗后的數據分為多個數據段,通過對各數據段同一時刻的記憶進行求和,并將求和結果的平均值作為標準記憶,以此消除不完整數據對狀態規律挖掘的影響;最后,根據數據段的質量高低對GRU的“記憶”進行更新,即數據質量好的多記,數據質量差的忘記。實驗結果表明,提出的預測模型在數據未濾波和濾波后的預測均方根誤差(Root Mean Square Error , RMSE)均低于 ARIMA 、LSTM和GRU 模型。
1 電力狀態大數據特性分析
狀態數據貫穿設備全壽命運行的整個時期,具有總量大(Volume)、增長快(Variability)、密度低(Value)等特點。并且,從圖1的光伏發電可知,新能源光伏發電數據以0.25h為單位進行采樣,故光伏發電的數據在總量、增長速度方面均比設備狀態數據大;此外,由于光伏發電易受氣候影響,其價值密度不僅低于狀態數據的價值密度,還多了圖1中周四光伏發電波動數據的無效異常數據。因此,本文以“迎刃而解”為思路(能挖掘困難的新能源發電數據規律,那也能挖掘較為簡單的狀態數據規律),對本文算法的有效性進行驗證。同時,為了便于比較,采用RMSE作為評價依據,計算公式如下:
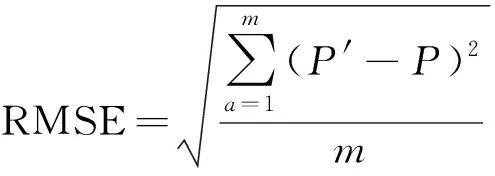
(1)
式中:′、分別為預測數據、現實數據。
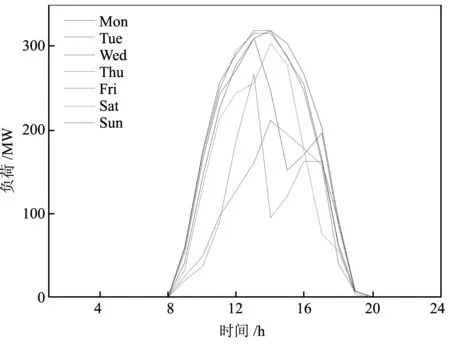
圖1 一周內光伏發電的負荷
由于光伏發電都在8之后,于是采用08:00-20:00的發電數據進行預測分析,ARIMA、LSTM、GRU預測準確度如表1所示,預測結果如圖2所示。結合表1和圖2可知,ARIMA預測準確率最低,RMSE達到了135,而LSTM及LSTM變體GRU的RMSE雖然比ARIMA較小,分別為41和39,但預測準確率依舊有待提高。由此可見,類似周四的異常數據不僅加大了數據規律挖掘的難度,還降低了挖掘算法的準確率。

表1 ARIMA、LSTM、GRU預測光伏發電的負荷與真實值的RMSE對比
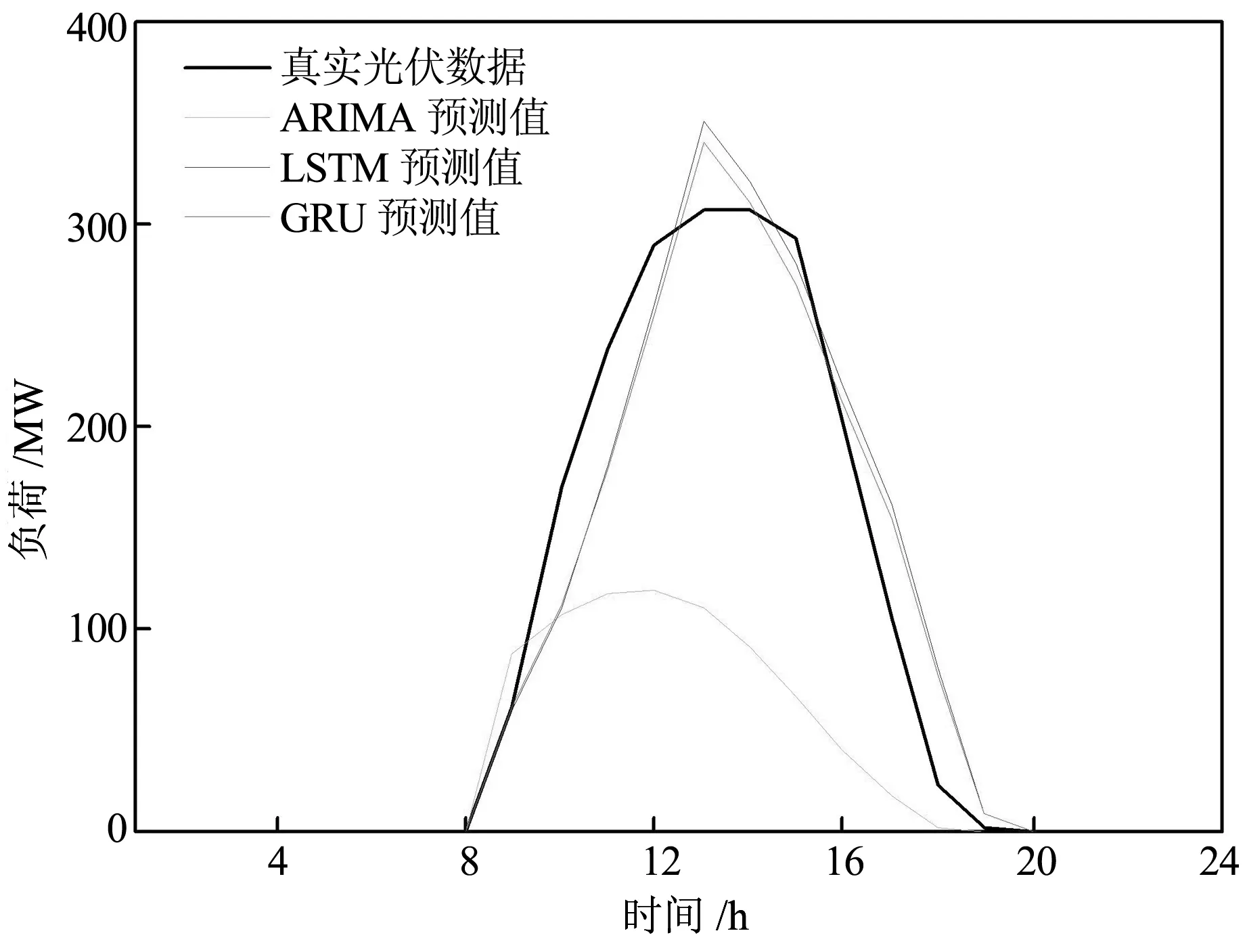
圖2 ARIMA、LSTM、GRU預測光伏發電的負荷與真實值的對比
2 基于改進GRU的電力大數據分析
從圖1可知,類似周四的數據由于受氣候影響,其波動性影響了整天發電數據的規律性,這些無效的異常數據造成當天發電數據呈現出一個假的“駝峰規律”性。因此,針對這些無效、異常數據的影響,以及當前算法的不足,本文通過數據質量改善和算法改進兩部分進行改進。
2.1 數據質量提升
針對無效、異常數據的影響,參照文獻[12],利用自適應小波濾波算法進行數據質量提升。傳統的小波濾波常用閾值選取公式為:
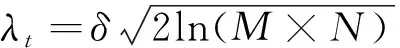
(2)
式中:、和分別為噪聲均方差、信號提升層數和信號范圍。由于無效異常值的出現是隨機不可預知的,無法得到數據和噪聲的統計特性先驗規律,故針對規律失真的情況,利用數據真實性定義其自適應閾值范圍,改進后的自適應閾值小波濾波為:
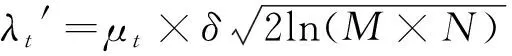
(3)
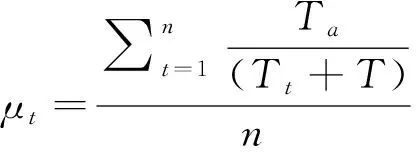
(4)
式中:和分別為當前采樣值和上次濾波結果。
2.2 改進GRU模型
作為LSTM改進體的GRU雖然簡化了輸入和輸出,即LSTM的輸入、輸出、忘記門簡化為更新門和重置門,但是依舊保持了LSTM預測準確率高的優點。標準的GRU門控邏輯如圖3所示,時刻GRU狀態輸出為:
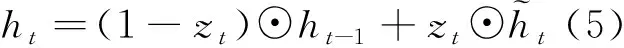
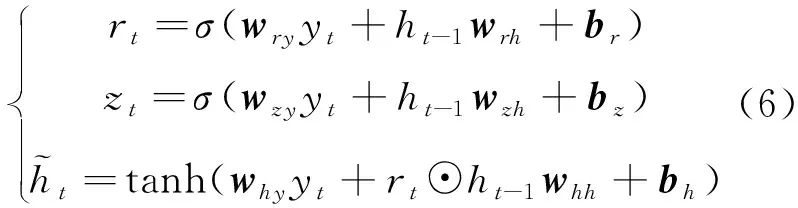
式中:、、和⊙ 分別為Sigmoid激活函數、權重矩陣、偏置向量和數據對應位置的點乘運算。
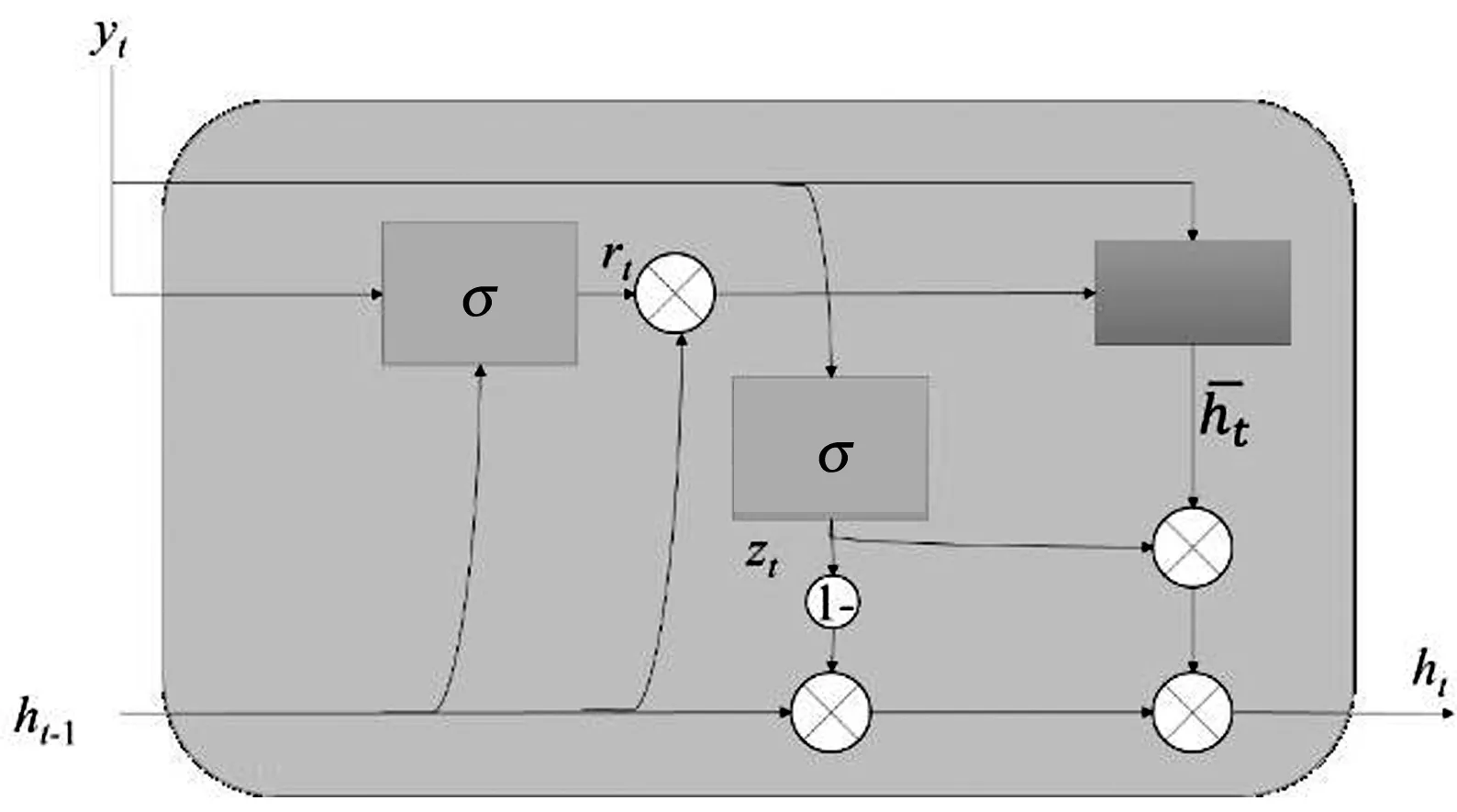
圖3 標準的GRU門控邏輯
從圖3中GRU的門控邏輯可知,重置門決定了如何將新數據與之前記憶結合,而更新門則決定了多少之前記憶的作用。因此,提高算法對無效異常數據魯棒性的關鍵在于如何和。為此,本文對GRU進行改進,改進后的GRU門控邏輯如圖4所示。本文根據自適應小波濾波對數據質量提升程度,將數據分為個周期段,將各周期段同一時刻的平均記憶作為標準記憶。利用標準記憶對GRU的重置門進行選擇性記憶,即數據質量高的多記憶、數據質量差的少記憶。改進后的GRU為:
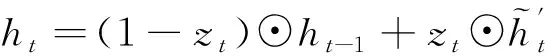
(7)
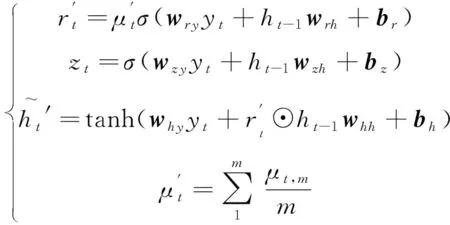
(8)
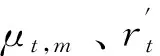

圖4 改進后的GRU門控邏輯
3 實驗分析
為了驗證本文模型在異常、無效數據影響情況下均具有較高的準確率和可靠性,進行了以下實驗。實驗分為兩部分:原始數據情況下不同算法之間對比和數據濾波后不同算法之間對比。從圖5和表2的對比中可知,無效異常數據導致的失真規律雖然對GRU的記憶造成了影響,但是本文對重置門進行了選擇性記憶,失真較大的規律被遺忘,預測準確率相對于ARIMA、LSTM和GRU分別提高了76%、16%和11%。
另外,經過本文方法濾波后的光伏發電數據的質量得以提升,以周三和周四數據改善結果最為明顯,數據上升沿和下降沿的失真得到了抑制。本文模型、ARIMA、LSTM和GRU利用濾波后數據進行預測的準確率相對于未濾波數據預測準確率分別提高了28%、56%、13%、13.8%;利用失真得到抑制的數據進行預測,本文模型預測準確率相對于ARIMA、LSTM和GRU分別提高了61%、30%和25%。
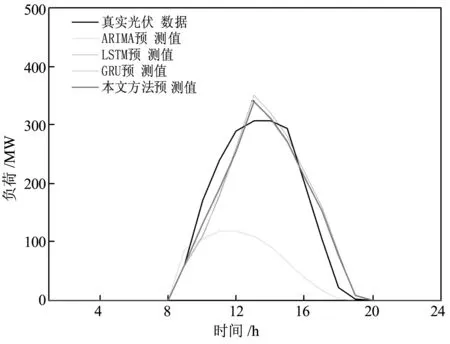
圖5 數據未濾波情況下,本文方法與ARIMA、LSTM、GRU預測結果對比
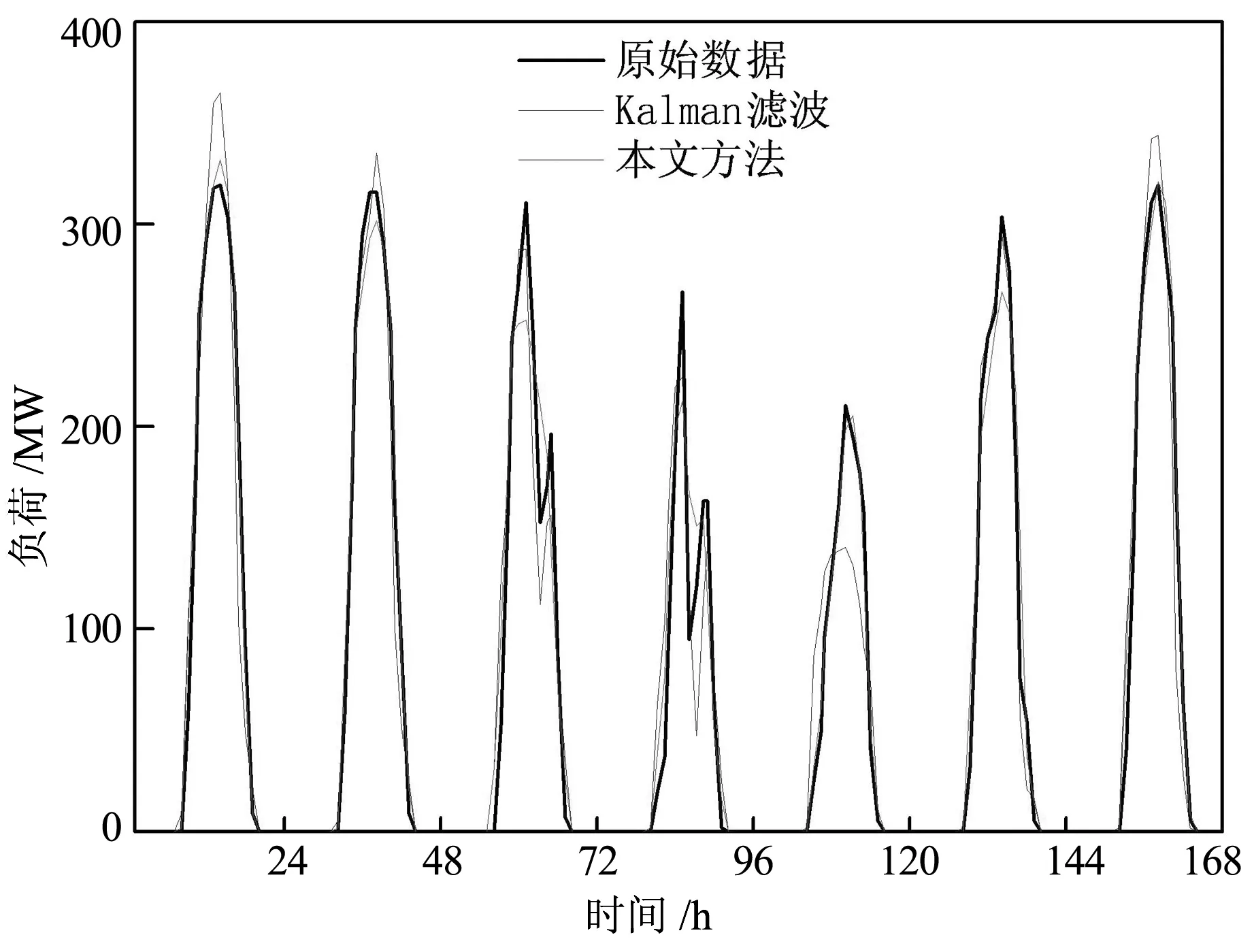
圖6 本文方法與Kalman濾波對數據質量提升情況對比
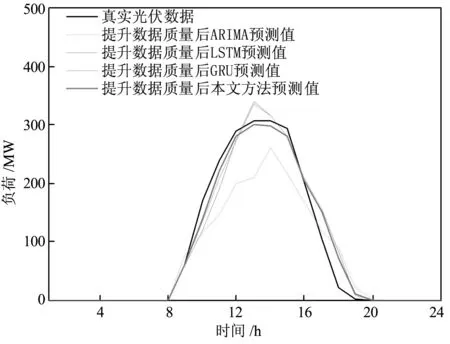
圖7 數據濾波后,本文方法與ARIMA、LSTM、GRU預測結果對比
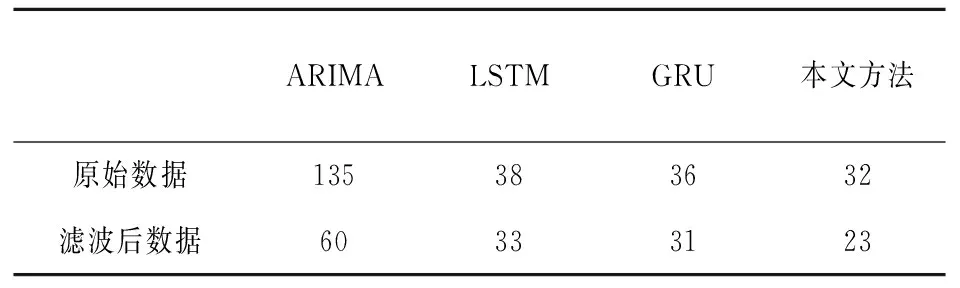
表2 ARIMA、LSTM、GRU和本文方法預測光伏發電的負荷與真實值的RMSE對比
4 結 論
針對電力大數據分析過程中存在無效、異常數據導致數據質量較差,以及當前數據分析方法難以在規律失真情況下分析真實規律的問題,提出了基于改進GRU的調控大數據分析模型。該模型采取自適應小波濾波的方法提高數據質量,降低數據規律失真率;并通過改進GRU的重置門的記憶細胞提高模型抗數據失真魯棒性。

