基于“四個理解”視角下的初中數學作業設計

張群偉

(伊寧市教育教學研究室，新疆伊寧，835099)

章建躍博士提出數學教學是基于理解數學，理解教學，理解學生，理解技術進行的思維與實踐活動.作業設計是教學中的必要環節，是課堂教學活動的延伸與補充，同樣遵循以上原則.

1 理解數學是設計高品質作業的前提

理解數學，從整體上把握數學結構，才能設計出目標清晰，內涵豐富的作業.只有題目有了準確的定位，具備承載學生發展的功能，才能設計出“少而精”的作業，實現針對性的訓練，從而減輕學生的作業負擔.

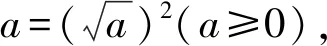
(1) 9；(2) 5；(3) 2.5；(4) 0.25；(5) 0.

該題是學習“二次根式(1)”后的作業之一.《義務教育數學課程標準(2011年版)》對二次根式的要求是“了解二次根式、最簡二次根式的概念，了解二次根式(根號下僅限于數)加、減、除運算法則，會用它們進行簡單的四則運算”，具體到本課時的教學目標，即為“根據算術平方根的意義了解二次根式的概念，知道被開方數必須是非負數的理由；能用二次根式表示實際問題中的數量關系”.本題是二次根式的簡單變形，這種變形在實數范圍內的因式分解中有用，也為后繼的一元二次方程的解法提供知識支撐.

作業設計要重視對教學內容的整體分析，不僅要體現知識點的反饋，也要關注知識點之間的聯系，幫助學生建立能體現學科本質、對未來學習有支撐意義的結構化的數學認知體系.

2 理解學生是設計高品質作業的關鍵

作業的設計要理解學生，關注學生的思維最近發展區.沒有針對性的作業，只會增加學生的學業負擔.所以因材施教，設計分層作業，滿足不同層次學生的需求，才能使作業真正發揮鞏固知識、深化知識、發展能力的作用.

例如，在新授課“多項式的因式分解(1)”后，筆者設計這樣一組作業：

A層：

(1) 下列各式從左到右的變形中，屬于因式分解的是( )

A. 6x2y=2x·3xy

B.x3-2xy=x(x2-2y)

C. (a+3)(a-3)=a2-9

D.x2+4x+1=x(x+4)+1

(2) 多項式9a2b-3ab2的公因式是.

(3) 若ab=7，a+b=6，則a2b+ab2的值為.

(提示：將多項式a2b+ab2分解因式，你發現了什么？)

(4) 把下列各式分解因式：

① 18a2b-8b；②m2n+mn；③ 2x2-12xy2+8xy3；④ 3x2(x-y)+6x(y-x).

(5) 利用分解因式方法計算：

① 1012-101；② 27×19.99+72×19.99+19.99.

B層：

(1) 下列因式分解正確的個數是( )

①x2-2x+1=(x-1)2；②x2-1=(x-1)(x+1)；③x2-2x=x(x-1)；④ 2x2-2x=2x(x-1).

A. 1個 B. 2個 C. 3個 D. 4個

(2) 多項式3ma3+6ma2-12ma的公因式是.

(3) 邊長為a、b的長方形，它的周長為12，面積為7，則a2b+ab2的值為.

(4) 把下列各式分解因式：

① -8a2b+12ab2-4a3b3；

② -24x2y-12xy2-28y3；

③ 2m(m-n)2-8m2(n-m)；

④ (x-y)2-x+y.

(5) 利用分解因式方法計算：

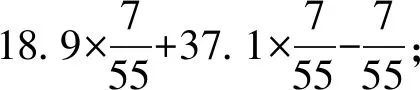
C層：

閱讀理解：把多項式am+an+bm+bn分解因式.

解法一：am+an+bm+bn=(am+an)+(bm+bn)=a(m+n)+b(m+n)=(m+n)(a+b)；

解法二：am+an+bm+bn=(am+bm)+(an+bn)=m(a+b)+n(a+b)=(m+n)(a+b).

觀察上述因式分解的過程，回答下列問題：

(1) 分解因式：m2x-3m+mnx-3n；

(2) 已知：a，b，c為△ABC的三邊，且a3-a2b+5ac-5bc=0，試判斷△ABC的形狀.

A、B層的作業設計都是5道題，題型一致，不同層次學生作業時長大體相當，分層后針對性強，能滿足部分學生學習需求.逐一比對，第一題問法由“屬于因式分解的是”到“下列因式分解正確的個數是”，問題從封閉走向開放.第二題在多項式的項上有變化，結構變復雜，能力要求也相應提高.第三題問題呈現方式不同，A層是直接呈現代數形式ab=7，a+b=6，且有提示：將多項式a2b+ab2分解因式，你發現了什么？B層則利用幾何形式，把ab=7用長方形的面積為7，a+b=6用長方形的周長為12來表述，考查學生轉化的能力，培養學生的探索精神.四、五兩題在難度上也有明顯提升.C層的作業是拓展拔高，充分發揮作業作為課堂延伸的功能，用閱讀題的形式讓學生關注知識學習的過程，學會用數學知識解決實際問題，感受數學的用處.

作業布置切忌隨意性、盲目性和一刀切的現象.“不同的人在數學上得到不同的發展”的理念在作業設計上的體現就是重視個體差異，關注學生可持續發展.

3 理解教學是設計高品質作業的保障

《義務教育數學課程標準(2011年版)》指出：在教學中教師要引導學生在真實情境中發現問題和提出問題，利用觀察、猜測、實驗、計算、推理、驗證、直觀想象等方法分析問題和解決問題.在作業的設計上結合生活中的現象，讓學生學會思考.

例如，在“代數式”的復習課后筆者選擇了下面問題：

當你記不住九九乘法表中乘9的口訣時，你可以進行如下的操作：

例如，伸出兩只手，做運算4×9時，如圖1，從左手開始數4下，數到第4根手指向下彎.這時，該手指左邊有3根手指，右邊有6根手指，可得36，即4×9=36.

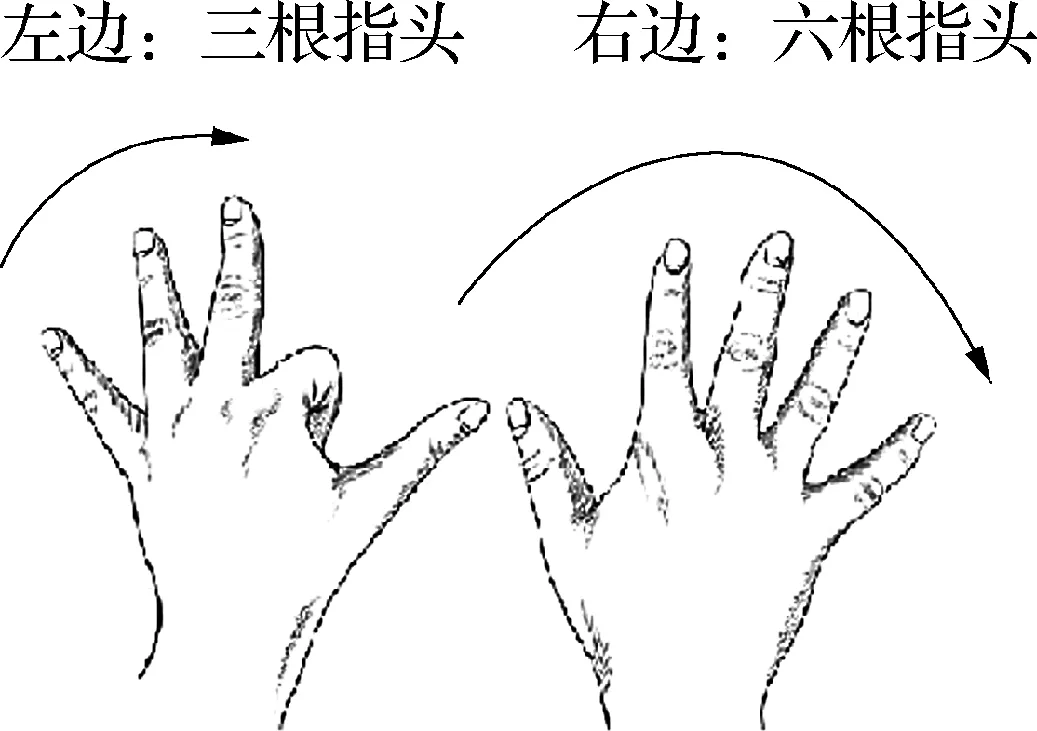
圖1

類似的，做運算8×9時，從左手開始數8下，數到第8根手指向下彎.這時，該手指左邊有7根手指，右邊有2根手指，可得72，即8×9=72.

……

將問題一般化，我們可以解決9n(1≤n≤9，且n為整數)的問題.從左手開始數n下，數到第n根手指向下彎.這時，該手指左邊有根手指，右邊有根手指.

列式計算說明上述操作的理由.(不能1～9逐個代入)

本次作業讓學生從身邊熟悉的現象中發現問題，用已有的數學知識去解決問題，考查規律性問題的解決，找到規律并進行驗證是解題關鍵.由此引發思考，乘8的口訣是否有這樣的規律？

只有作業聯系生活實際，學生感受到數學有用，才能夠以數學的眼光觀察世界、以數學的思維分析世界、以數學的語言表達世界.

4 理解技術助力高品質作業的設計

合理利用現代信息技術，可以提升學生的探究熱情，開闊學生的視野，激發學生的想象力，提高學生的信息素養.技術的應用在預習作業的設計上更有優勢，可以化抽象為直觀，發現不變的數學本質.

例如，在“圓周角(1)”課前，筆者讓學生利用GeoGebra對進行預習.

學生通過軟件，可以量出⊙O中AB所對的圓周角∠ACB和圓心角∠AOB的度數，改變C的位置觀察兩者度數的變化，得到不變的結論：∠AOB=2∠ACB.學生觀察圖3，利用已有的知識經驗，可知∠AOB=2∠ACB，若點C在⊙O上，一般化(圖2和圖4)的證明，又如何完成？對于初三學生，利用轉化思想，通過連接CO并延長交⊙O于P，把圖形分解為兩個基本題型(圖3)進行解決.

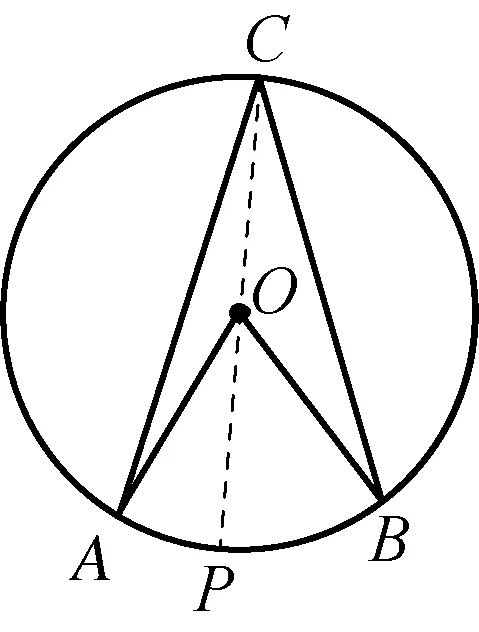
圖2

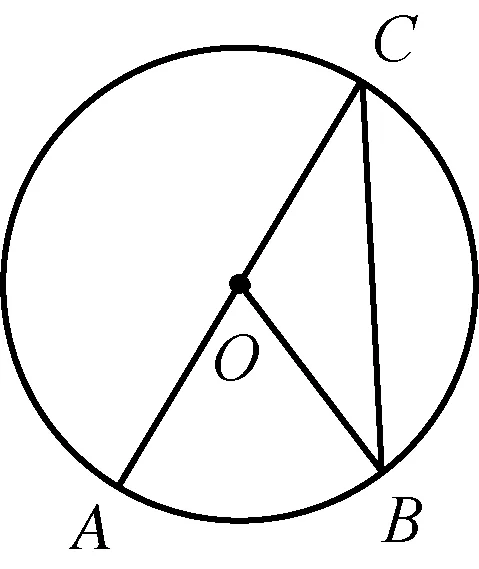
圖3

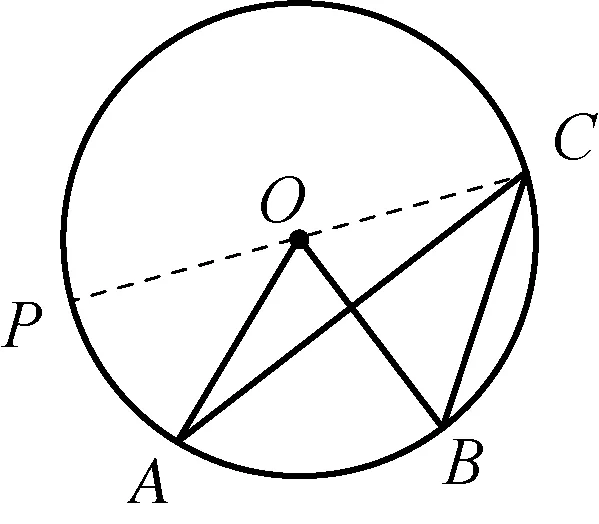
圖4

部分學生通過數學實驗，又發現：當點C在圓上運動時候，∠AOB=2∠ACB；當點C在圓外，∠AOB>2∠ACB；當點C在圓內，∠AOB<2∠ACB.實驗的結果已經超出了文本提供的圓周角定理.技術的引入，使得數學問題直觀化，便于學生發現問題和提出問題，激發數學探究熱情.

教師要樹立正確的作業觀.站在理解數學、理解學生、理解教學、理解技術的視角下提高作業設計的質量，減輕學生課業負擔，充分激發數學學習的主動性與積極性，幫助學生學會學習，發展學生的核心素養、促進學生全面發展.