基于數據驅動的無線傳感器網絡擁塞控制
楊美艷
(天津科技大學 人工智能學院, 天津 300457)
無線傳感器網絡(WSNs)具有規模大、動態性強、自組織網絡的特性[1],是當前普遍使用的主要網絡結構之一.隨著WSNs應用范圍的擴展以及應用率的提升,網絡負擔急速提升.由于WSNs內包含大量節點,各節點緩存資源受限[2],且網絡整體帶寬較小,結合WSNs網絡獨特的多對一通信模式,極易造成數據幀堆積在節點緩沖區中,形成網絡擁塞問題,導致數據包丟失以及網絡吞吐量下降等問題[3],降低WSNs應用性能.因此,研究一種有效的WSNs擁塞控制方法具有重要意義.
當前相關領域專家所研究出來的擁塞控制方法大多以SDN(軟件定義網絡)數據中心網絡為核心實現網絡擁塞控制[4].WSNs擁塞在整體上可分為節點級擁塞與鏈路級擁塞兩種類型,前種擁塞描述的是節點發生的流量信息高于自身能力,造成緩存過量與數據丟失等問題;后種擁塞描述的是若干個節點通過使用一個無線信道時,由訪問沖突形成的鏈路利用率與吞吐量下降等問題[5].以SDN數據中心網絡為核心的控制方法只考慮節點擁塞的控制,對鏈路擁塞的控制效果并不顯著.
基于計算機科學的數據驅動控制是一種全新的控制理念[6],是控制器控制設計過程中忽略數學模型信息,僅考慮受控系統離線與在線I/O數據與數據處理所得信息,同時基于相應的假定條件實現的一種有效的控制方法[7].針對WSNs節點與鏈路的雙重擁塞問題,將數據驅動控制理念應用其中,提出基于數據驅動的WSNs擁塞控制方法,實現MAC層與數傳層相結合的跨層擁塞控制.
1 無線傳感器網絡擁塞控制方法
1.1 基于數據幀監察的WSNs擁塞判斷
在WSNs內監察到附近節點傳輸數據時,利用被動監察的方式判斷WSNs擁塞情況[8].以傳輸節點A為例進行說明,在其正常傳輸數據幀功能的基礎上,具有被動監察附近節點傳輸數據幀的功能,可確定這些數據幀的傳輸節點地址,判斷傳輸節點的活躍度,以此確定節點的擁塞情況,詳細過程描述如下:
1) 傳輸節點A正常傳輸數據,同時監察附近節點傳輸的數據幀,分析其數據幀的傳輸節點地址.MB(A)表示Ts時間內節點A監察到某節點傳輸數據幀的數量,在設定時間Ts內,每確定節點B輸出的數據幀,則MB(A)值加1.
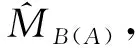
3) 節點A利用式(1)確定最近一個Ts時間內監察到的附近節點傳輸數據幀次數均值為
(1)
式中,m為數據幀傳輸節點數量整體值.
4) 由于WSNs內節點擁塞的主要原因為網絡狀態的不間斷性與其他節點對擁塞問題的處理能力[9],因此,分別分析節點與自身歷史狀態相比的活躍度ξhB(A)和與其他節點相比的活躍度ξrB(A),其表達式為
(2)
(3)
5) 對ξhB(A)和ξrB(A)實施歸一化處理,通過式(4)表示利用節點A判斷的節點B擁堵度量化值φB(A),即
(4)
在φB(A)值大于1的條件下,可定義節點B未處于擁塞狀態;在φB(A)值小于1的條件下,可定義節點B處于擁塞狀態,且其值越小,說明節點擁塞狀態越嚴重[10].針對存在擁塞狀態的節點,利用離散滑模擁塞控制器進行擁塞控制.
1.2 離散滑模擁塞控制器設計
1.2.1 離散指數趨近率
離散指數趨近率s(k)計算公式為
ps(k)
(5)
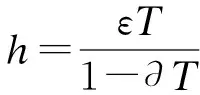
1.2.2 自適應離散滑模控制器設計
由于WSNs具有顯著的復雜性與時變性[11],因此,在設計控制器完成其擁塞控制過程中引入滑模控制理論.為了確保達到滑動模面上的滑模運行趨于平穩[12],令路由器的隊列長度達到期望值標準,控制器離散滑模面可表示為
s(k)=Le(k)
(6)
式中:L為0~1之間的值;e(k)為誤差.
根據霍爾維茲多項式標準的定義,判斷其是否符合霍爾維茲多項式標準[13].在WSNs處于一階狀態時,L值為0,預期誤差為
e(k)=Xd-X(k)
(7)
式中,Xd和X(k)分別為預期輸出與實際輸出.
二階離散WSNs狀態方程為
X(k+1)=aX(k)+bU(k)
(8)
式中:U(k)為節點在k時刻的離散滑模控制律;a和b為常數項.
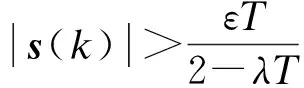
(9)
1.3 基于數據驅動的控制策略
針對離散滑模擁塞控制器,根據節點間的關聯性設計基于數據驅動的控制策略[14].若WSNs內兩個不同節點傳輸的數據幀同時占用同一信道(即鏈路擁塞),參考數據驅動理論,依照優先傳輸節點輸出流量小的數據幀,輸出流量相對較大的數據幀就近選取其他信道進行傳輸.
1.3.1 節點獨立
在WSNs內節點間不存在關聯的條件下,節點的輸出可描述為
(10)
式中:X(k+1)=(X1(k+1),X2(k+1))T;Δu(k)=(u1(k)-u1(k-1),u2(k)-u2(k-1));δ1(k)與δ2(k)為WSNs的偽偏導數.
在此條件下,令WSNs輸出與預期輸出一致,離散滑模擁塞控制器控制策略為
(11)
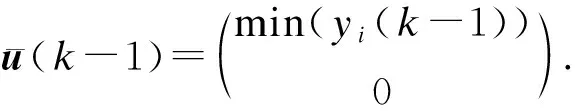
在式(11)的控制策略下能夠實現WSNs實際輸出與預期輸出的跟蹤,使曲線傳感器網絡達到平穩狀態,不會形成擁塞問題.
1.3.2 節點關聯
在WSNs內節點間存在關聯的條件下,節點的輸出可描述為
(12)
式中:σ12和σ21為常數;δ1(k)δ2(k)≠σ12σ21.在此條件下,令WSNs輸出與預期輸出一致,離散滑模擁塞控制器控制策略為
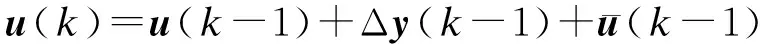
(13)
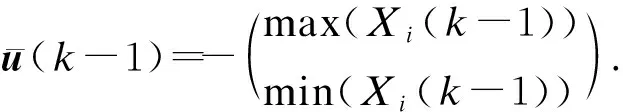
在上述控制策略下,WSNs不會產生節點級與鏈路級擁塞.
2 仿真測試結果與分析
2.1 測試對象
為了驗證基于數據驅動的WSNs擁塞控制方法的應用效果,以圖1中的WSNs結構為測試對象,針對瓶頸節點7,利用本文方法與傳統方法對其進行擁塞控制,驗證本文方法的應用效果.
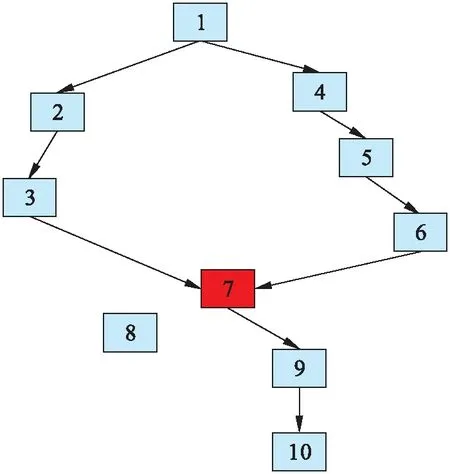
圖1 測試對象拓撲結構Fig.1 Test object topology
2.2 節點內隊列長度
圖2為測試對象節點7內數據隊列在240 s內的波動情況.分析可知,采用本文方法進行擁塞控制前,該節點內數據隊列長波波動較為顯著,說明該節點的運行處于不穩定狀態;采用傳統方法進行擁塞控制后,節點內數據隊列長度波動有所改善,但該節點運行仍處于不穩定狀態;采用本文方法進行擁塞控制后,節點內數據隊列長度波動平緩,說明該節點處于穩定運行狀態.由此可知,采用本文方法進行節點擁塞控制更能降低節點內數據隊列長度的波動性,令節點正常運行.
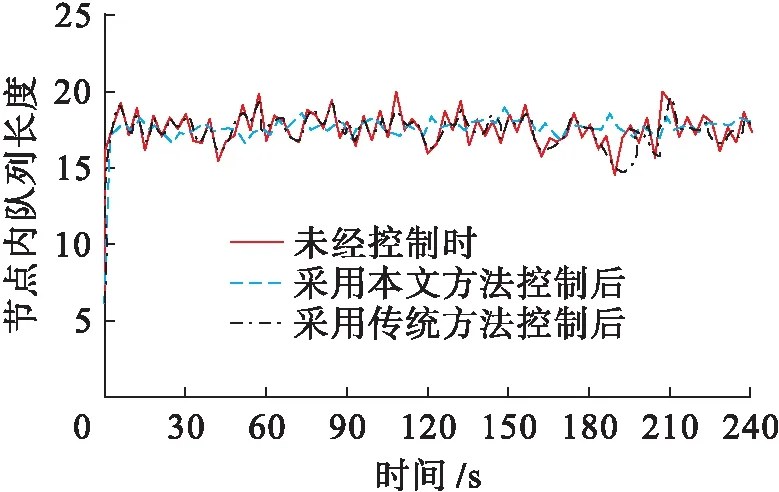
圖2 節點隊列變化Fig.2 Node queue variation
2.3 吞吐量
圖3為采用本文方法控制前后,測試對象節點7的數據吞吐量變化情況.采用本文方法控制節點擁塞情況后測試對象節點的吞吐量與采用本文方法前及經傳統方法控制后相比均顯著提升,采用本文方法進行測試對象節點擁塞控制更能顯著提升節點的數據傳輸能力.這是由于采用本文方法進行節點擁塞控制后,數據傳輸的窗口尺寸提升,因此,單位時間內數據傳輸量提升.
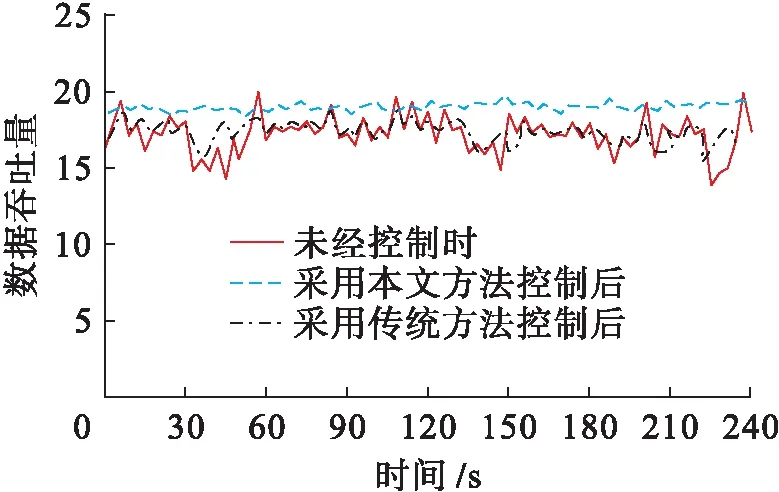
圖3 吞吐量變化Fig.3 Throughput variation
2.4 節點信道擁塞標記率
圖4為采用本文方法進行節點信道擁塞控制前后,節點信道擁塞標記概率的變化情況.由圖4可知,未采用任何方法進行節點擁塞控制前,在節點信道擁塞條件下,其余節點受網絡整體狀態影響顯著,因此節點數據傳輸信道被標記的概率具有顯著的隨機性與概率性.采用傳統方法進行節點擁塞控制后,節點數據傳輸信道被標記的概率的隨機性與概率性有所改善,但效果并不理想.采用本文方法進行節點擁塞控制后,節點數據傳輸信道被標記的概率具有較強一致性,擁塞控制概率約為4.5%,優于傳統方法,這是由于采用本文方法控制后,節點擁塞現象被有效解決,其余節點不受該節點擁塞問題影響,沒有被標記,因此,測試對象內節點數據傳輸信道被標記的概率具有較強一致性.
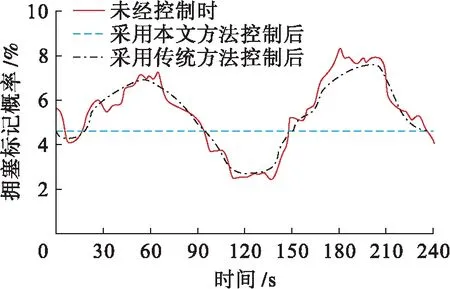
圖4 節點信道擁塞標記率變化Fig.4 Mark rate variation of node channel congestion
2.5 控制器自適應律曲線
圖5為本文方法中控制器的滑模自適應律曲線.由圖5可知,相比傳統方法,本文方法設計的控制器能更好地跟蹤目標值,響應時間更快,可控制在100 ms左右,并且不存在顯著抖動,能較好地實現測試目標擁塞控制.
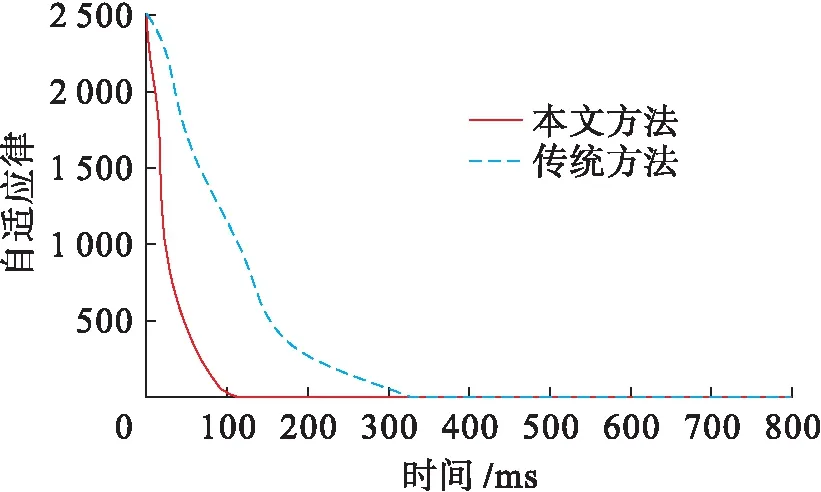
圖5 滑模自適應律曲線Fig.5 Curves of sliding mode adaptive law
3 結 論
隨著WSNs應用范圍的擴展,人們對WSNs的應用性能提出更高要求.網絡擁塞是WSNs應用過程中普遍存在的問題,因此針對該問題的解決方案研究極為重要.本文研究基于數據驅動的WSNs擁塞控制方法,以此解決WSNs內節點與鏈路的擁塞問題.測試結果顯示,本文方法可有效降低節點內數據隊列長度的波動性,提升單位時間內數據傳輸量,使節點信道擁塞標記率控制在4.5%左右,具有一致性,響應時間控制在100 ms左右,可顯著提升WSNs的應用性能.

