順北油田某區塊三維地應力場有限元精細建模與分析

陳修平， 沈新普， 劉景濤， 沈國曉

(1. 中國石化西北油田分公司 石油工程技術研究院， 烏魯木齊 830001； 2. 中國石化縫洞型油藏提高采收率重點實驗室， 烏魯木齊 830001； 3. 中國石油大學(華東) 石油工程學院， 山東 青島 266580)

順北油田是塔里木盆地北部區域的主要碳酸鹽儲層油田.順北油田所在區域有13條斷裂帶，地層裂縫較多.由于經歷了多次地質構造運動，油田區塊各處局部應力分布復雜，難以準確預測，從而導致無法準確計算安全泥漿窗口.實際鉆井工程中井壁坍塌和泥漿漏失嚴重，發生鉆井事故風險較高[1-2].本文的任務是結合順北5號斷裂帶北部破碎性地層的單井實測信息及鉆井工程中的阻卡情況，對目標區塊三維地應力場進行精細化有限元建模計算，得到區塊地應力的三維有限元空間分布數值結果，為鉆井安全泥漿密度窗口進一步的選擇提供理論依據和準確的參考數據.

區塊地應力場的精準構建是近年來國內外工程力學的研究熱點之一，若干研究者進行了不同的嘗試[3-5]，采用不同的技術方法得到的地應力場各有特點.準確建立三維地應力場主要難點在于：1)主應力數值結果的大小與相應的實測值大小和實測值的方向不易同時滿足，如果保證主應力分量大小的計算值和實測值一致，計算和實測結果的主方向則不容易保證一致；強調主應力計算結果和實測值的方向一致，則很難保證二者的大小一致.若干關于地應力場分析的文獻中主應力結果與實測值的大小和方向均存在差別.2)碳酸鹽儲層的材料特性比較復雜，試驗測量數據較少.

隨著地質測量技術和計算技術的發展，近年來三維精細地應力場建模技術有了長足進步[6-8].目前解決上述問題的方法主要有：1)通過引入區塊三維地震波數據，建立基于地震波的三維地質模型，在該三維地質模型的基礎上建立三維區塊有限元力學模型.2)進行單井地質力學分析，通過測井數據及鉆井實測信息來計算地層材料參數，并確定所在井位上各個深度的地應力分量.3)根據單井地質力學分析結果和實測數據來建立區塊地應力場的初始輸入參數，并進行有限元數值計算，然后把三維有限元數值計算結果與單井實測結果相比較，根據兩者誤差精度情況改進輸入參數取值，直到數值結果和實測結果兩者精度位于合理范圍.單井實測結果包括用地漏試驗方法得到的最小水平主應力值，以及根據影像測井分析得到的最大水平主應力的方向.圖1為三維精細地應力場的有限元建模與分析流程圖，其中，Sh為最小水平主應力，SH為最大水平主應力.

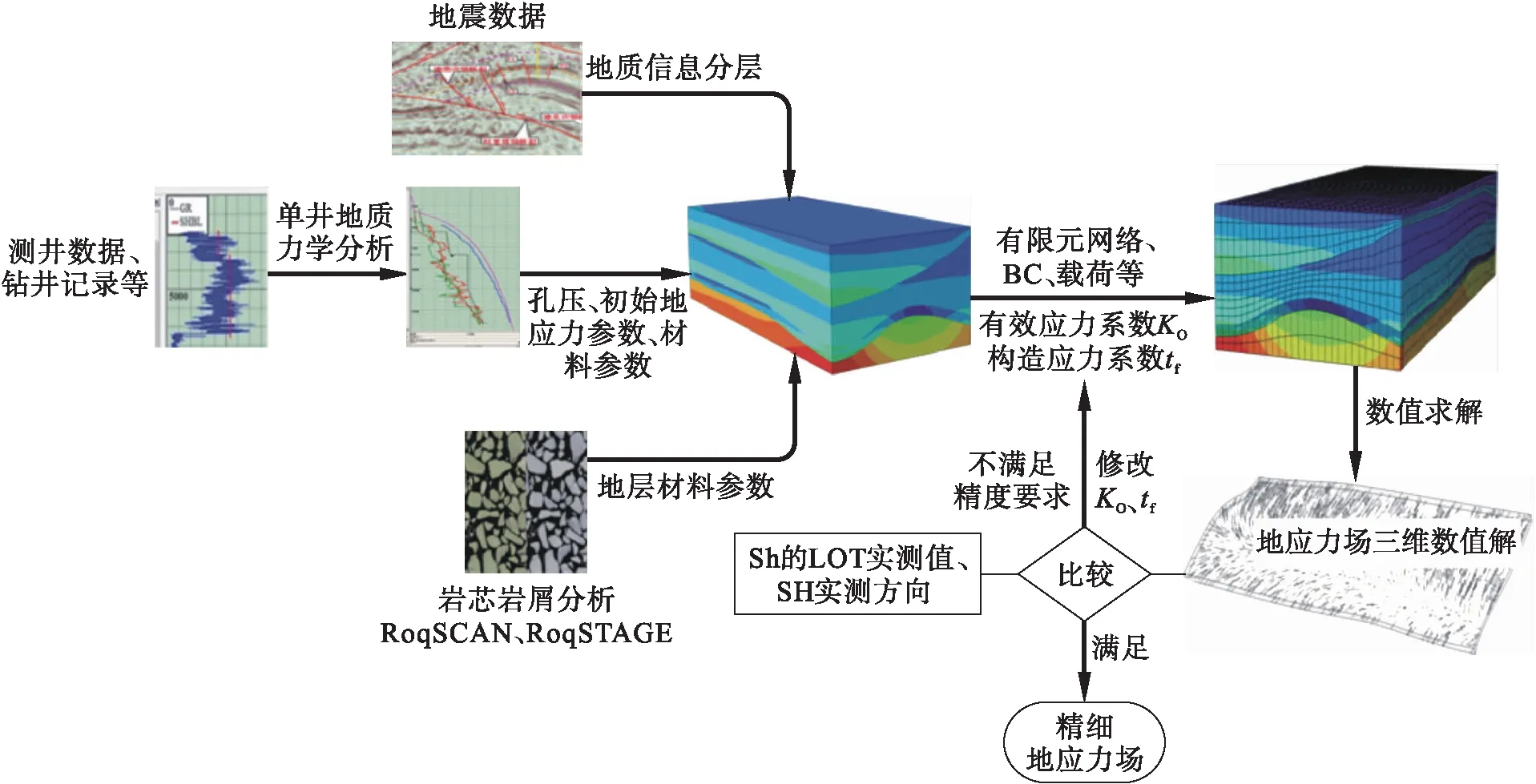
圖1 精細地應力場的技術路線流程圖Fig.1 Flow chart of technical route for refined geostress field

1 順北油田某區塊三維有限元模型

圖2為本文根據地震波數據并結合單井層位信息建立的順北油田某區塊的三維地質模型.模型中包括了11個地層，各層之間以地質分層界面為界，分別為：地表-T30界面；T30-T33界面；T33-T46界面；T46-T50界面；T50-T56界面；T56-T60界面；T60-T63界面；T63-T70界面；T70-T74界面；T74-T76界面；T76-模型底面，共11個地層.這里的T30至T76為根據地層沉積年代確定的層面.在該區塊中，奧陶系碳酸鹽油層的位置在T74-T76地層，深度約為7 000～7 600 m之間.

圖2中區塊地質模型長寬高尺寸分別為：長55 km，寬26 km，深度約9 980 m.地表海拔約為985 m，接近平坦.最下層是為了引入位移約束而加的一個層位.下底面設為平面.圖2b為從地質模型轉換而來的有限元網格.圖2c為T74-T76奧陶系碳酸鹽的油層網格.圖中紅點為A井目的層位置.有限元計算模型采用了127 765個C3D8R單元、137 088個節點對區塊幾何體進行離散.

2 單井地質力學分析

圖3為A井的測井數據以及根據測井數據計算得到的地層參數.測井數據包括地層的伽馬射線、壓縮聲波時長和剪切聲速時長；地層參數包括楊氏模量、泊松比、密度.在計算楊氏模量和泊松比等地層參數時，采用了文獻[9-11]給出的經驗公式和計算原理.

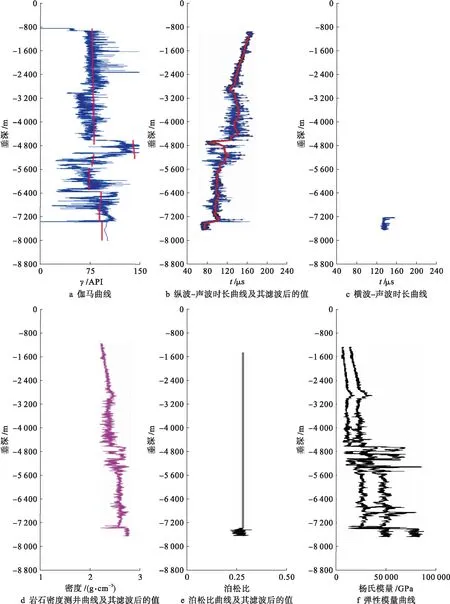
圖3 A井的測井數據和地層參數Fig.3 Logging data and stratum parameters of well-A

圖4為A井單井的地應力分析結果.圖4中各曲線分別為：紫線為垂向應力，藍線為最小水平主應力，該最小水平主應力在5 400 m左右深度上的值與地漏試驗點(紅方塊符號)相重合，說明該最小水平主應力曲線結果是合理的.細黑色曲線是最大水平主應力結果.粗黑色曲線為實際采用的泥漿密度曲線.在約4 800 m深度進行一次地漏試驗，測得的漏失發生時的泥漿壓力LOP用淺藍色方塊表示.在深度約7 500 m位置上有井漏發生，表明這兩個位置上的地層中天然裂縫較多.在7 200 m深度上，發生過一次鉆具阻卡，表明該位置上的鉆井液/泥漿密度很接近坍塌壓力，泥漿密度的安全系數不足.紅色曲線代表計算得到的坍塌壓力，即泥漿密度窗口下限.橄欖綠曲線代表地層孔隙壓力分布曲線.

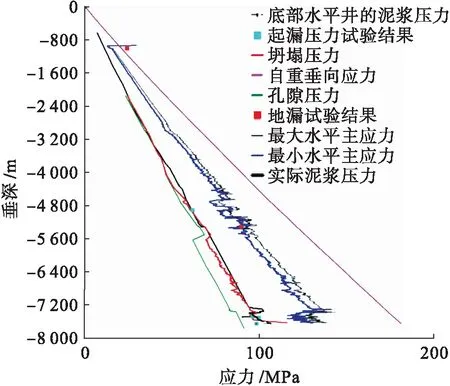
圖4 A井的單井地應力分析結果Fig.4 Analytical results of single-well geostress for well-A

在距離地表1 000 m以內的范圍內，由于種種原因，聲波時長等測井數據缺少或精度不夠，故1 000 m以上的單井分析結果不能使用.

3 區塊地質力學有限元分析結果

使用圖2中給出的三維有限元網格，將圖3～4的單井分析結果和前述最大水平主應力方向等參數作為輸入數據，建立了目標區塊地應力場的有限元模型.該有限元模型的邊界條件為四個側面和底面的法向零位移約束.載荷為重力載荷，初始地應力參數的設置根據單井地應力分析結果確定.

為了體現彈性模量隨深度變化的特性，把彈性模量的大小設為深度的函數，設計了用戶子程序來實現這一模型功能特點.經過數值計算得到的三維有限元地應力分析數值結果如圖5～7所示.

圖5中最大水平主壓應力方向接近正北方向.這與圖6給出的T74-T76地層的最大水平主壓應力方向不同，有超過20°的變化.該現象背后的主要原因是：不同的地層對應的造山運動方向不同，從而產生的構造應力方向也不同.

圖5 上部T30-T33地層中最大水平主壓應力的數值解Fig.5 Numerical solution of maximum horizontal principal stress in upper T30-T33 stratum

圖6 T74-T76地層中最大水平主壓應力方向Fig.6 Direction of maximum horizontal principal stress in T74-T76 stratum

圖7 下部T74-T76地層中最小水平主壓應力方向Fig.7 Direction of minimum horizontal principal stress in lower T74-T76 stratum

由于區塊的應力模式屬于“正斷層應力”模式，即豎向應力為最大的主壓應力分量，因此沿最小水平主壓應力方向的鉆井將具有最佳的井壁穩定性，也就是最佳的井軌跡方向.

圖8為地應力場三維數值解的三個主應力分量在A井位置上隨深度變化的分布曲線及其與A井的單井地應力分析結果的比較.圖8中，Shminc為最小水平主壓應力，Shmaxc為最大水平主壓應力，Sv為豎向應力，3D為三維數值解，1D為單井解析解.

圖9為圖8結果在下部6 000～7 400 m深度段的地應力主分量解析解與數值解比較局部放大圖.由圖9可以看出，三維精細地應力場數值解在A井位置上與單井地應力分析數值十分接近，最大差別不到10 MPa，相對誤差小于8%.圖8中，由于上部網格劃分得比較粗，對應的上部地應力數值很粗糙.

圖8 地應力場三維數值解和單井解析解比較Fig.8 Comparison of 3D numerical solutions of geostress with their single-well analytical counterparts

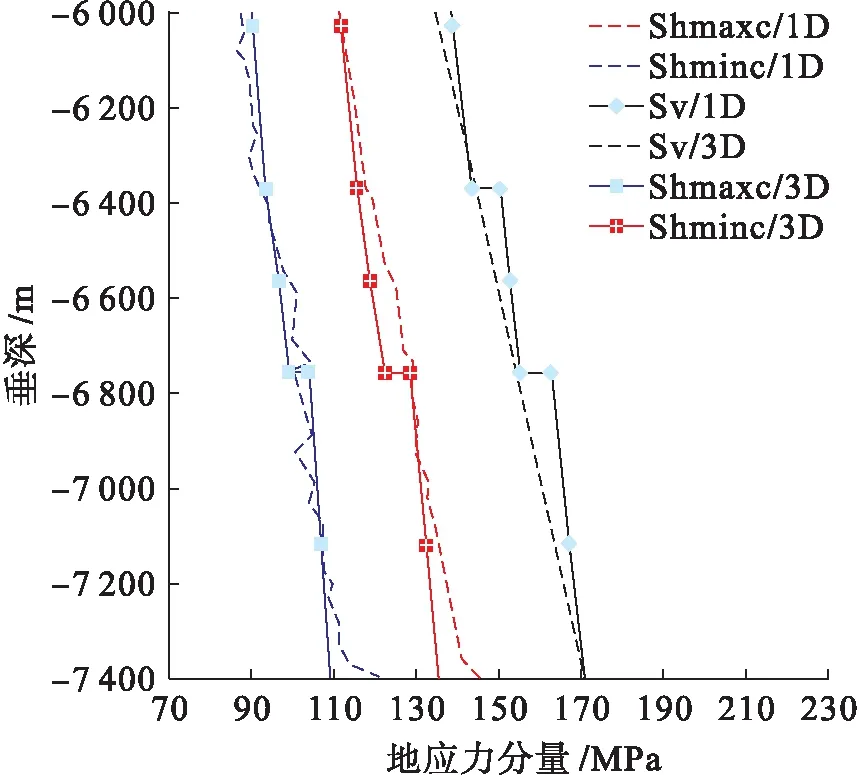
圖9 在下部深度上三維數值解和單井解析解比較Fig.9 Comparison of 3D numerical solutions at lower depth section with their single-well analytical counterparts

4 結 論

本文采用“綜合三維地質體和單井地應力分析結果”的方法，為順北油田某區塊建立了三維精細地應力場.首先根據區塊地震波數據信息建立精確的地質層位模型，并結合各個單井位置上的測井信息，校正/完善三維地震信息中得來的地層層位信息，得到完善的三維區塊地質模型.該建模做法保證了結構變化引起的地應力方向變化能夠得到準確體現.

由于區塊模型進行地應力場有限元分析的主要目的是通過模型分析得到儲層位置上精確的地應力場方向和主應力分量幅值的分布，結構模型最上面的上覆地層構造細節可以適當簡化處理，以此來減小計算量.但是所對應的應力數值解在最上面地層中的分布比較粗糙.采用單井測井數據來計算地層材料和初始地應力相關參數，能夠減少實測參數不足造成的輸入參數不確定性，保證精細地應力場模型輸入參數的準確性.

與實測結果相比，本文模型所得到的三維精細地應力場中最大主壓應力的方向在A井位置上與實測值符合.最小水平主應力的數值解和A井位置上對應的解析解相比，誤差小于8%，說明本文得到的精細地應力場數值解具有合理的精度.