FRFT域能量譜模擬電路故障特征提取方法

廖 劍，黃 詰，戴邵武，梅 丹，楊 術(shù)，馮 迪

（1.贛南師范大學，江西贛州 341000；2.海軍航空大學，山東煙臺 264001；3. 91899部隊，遼寧葫蘆島 125000）

0 引言

隨著模擬電路的廣泛應(yīng)用，模擬電路的故障診斷和性能評估成為研究人員關(guān)注的焦點，學術(shù)界針對此問題展開了大量研究并取得了一系列成果。然而，相較于數(shù)字電路，模擬電路由于自身原因，其故障診斷主要存在以下問題：1）由于模擬元器件參數(shù)的連續(xù)性，故難以為其定義通用的故障模型；2）由于模擬元器件的容差效應(yīng)，使模擬電路存在廣泛的非線性；3）實際被測電路的測試節(jié)點通常受限。傳統(tǒng)的模擬電路故障診斷方法，例如故障字典、參數(shù)識別方法已經(jīng)不能滿足實際需求。隨著人工智能技術(shù)的發(fā)展，神經(jīng)網(wǎng)絡(luò)、支持向量機和深度學習等因其為模擬電路的故障診斷提供了可行的技術(shù)支持，已被廣泛應(yīng)用。這些方法中，特征提取不僅在性能診斷中發(fā)揮著重要作用，而且對故障診斷的結(jié)果也具有影響作用。

近年來，學者們提出了多種模擬電路故障的特征提取方法，包括時域特征、頻域特征和統(tǒng)計特征（范圍、均值、標準差、峰度和熵）等。采用從可及節(jié)點直接采集靜態(tài)電壓或電流來構(gòu)造故障特征集的方法，雖操作方便簡單，但容易喪失電路狀態(tài)的動態(tài)信息。針對特定電路構(gòu)造目標函數(shù)，提取電路最優(yōu)響應(yīng)頻率也是常用方法。文獻[13]采集電路頻率響應(yīng)曲線構(gòu)造概率密度函數(shù)，在最大化特征辨識力的同時，最小化特征間的冗余信息，提取最優(yōu)頻率作為特征值，方法極其復(fù)雜，且缺乏通用性。采用信號處理方法對電路響應(yīng)信號進行分析，是當前研究的重點。文獻[15]采集節(jié)點信號進行傅里葉變換（Fourier Transform，F(xiàn)T），在頻域中進行分析，無法提供信號的任何時域信息，且不能處理非平穩(wěn)信號；文獻[16]選擇db2小波作為小波基函數(shù)，對響應(yīng)信號進行5 層多分辨率分解，得到6個分解系數(shù)序列構(gòu)造特征集，可能導致信號有效成分的損失；文獻[17]也采用小波變換（Wavelet Transform，WT）提取關(guān)鍵點響應(yīng)信號在低頻和高頻頻帶的能量構(gòu)造特征，但如何選取最優(yōu)小波函數(shù)仍是難點。

當前，分數(shù)階時頻變換方法受到越來越多研究者的重視，應(yīng)用領(lǐng)域不斷擴大，如應(yīng)用于模擬電路的故障特征提取。與傳統(tǒng)時頻分析相比，分數(shù)階時頻分析可以看作是1 種廣義時頻分析法，其具有無窮多個變換空間，能展現(xiàn)出更多的信號局部特征。Luo、Song 等基于分數(shù)階傅里葉變換（Fractional Fourier Transform，F(xiàn)RFT），提出了基于最優(yōu)FRFT域的模擬電路故障特征提取方法。此類方法受FRFT的時頻平面旋轉(zhuǎn)原理啟發(fā)，認為在時頻平面上存在耦合的故障響應(yīng)信號，在旋轉(zhuǎn)到合適的分數(shù)階平面上時可以解耦，使得原本難以區(qū)分的信號在FRFT 域中變得相對容易。因此，文獻[14][21]都是將采集的原始時域數(shù)據(jù)映射到某一FRFT域空間中，試圖在合適的FRFT域中完成故障的分類，以類別可分性測度為目標，利用智能尋優(yōu)算法，搜索最優(yōu)的分數(shù)階值，認為在相應(yīng)的階FRFT 域空間中，各故障狀態(tài)下的響應(yīng)信號可分性最佳并驗證了其可行性。基于FRFT的故障特征提取方法避免了小波基函數(shù)的選擇問題，同時，算法中的值還增加了該方法的靈活性。

盡管基于最優(yōu)FRFT的模擬電路故障特征提取提供了1種新方法，然而，如何快速地確定FRFT的最優(yōu)值卻是個難點，這需要經(jīng)過大量的計算。由于算法僅僅考慮了信號在1個最優(yōu)FRFT域的特征變換，而忽略了在其他FRFT 域中的信號特性，故提取的故障特征信息有限。文獻[18][20]分別利用FRFT 計算輸出節(jié)點的分形維數(shù)和的信息熵提取特征，但分形維數(shù)的計算復(fù)雜度高，信號的采集在實際中較難操作。因此，受FRFT 時頻旋轉(zhuǎn)變換特征提取信息理念的啟發(fā)并針對上述方法存在的不足，本文提出1 種在FRFT 全域空間中，將計算相應(yīng)時頻域的局部化特征作為故障特征的方法，通過把時域空間中的響應(yīng)信號映射到不同的FRFT域中，分別計算不同階FRFT域下原信號的能量譜峰值并將其作為故障特征。實驗中，將本文方法與其他特征提取方法進行比較，驗證了本文方法能顯著增強不同故障特征的可分性，從而提高故障診斷準確率，同時，時間復(fù)雜度也有明顯改善。

1 基于FRFT域能量譜峰值的特征提取

1.1 FRFT

1993 年，D.Mendlovic 和H.M.Ozaktas 提出FRFT，它是1 種在時頻域內(nèi)表示信號的新方法，克服了傳統(tǒng)FT 單一頻率變換的特點，是1 種統(tǒng)一的時頻變換，具有時域和頻域的雙域特性。近幾年，F(xiàn)RFT引起相關(guān)研究人員的關(guān)注，使諸如信號分析、模式識別等得到了廣泛和成功的應(yīng)用。

通常FRFT 可以有若干種不同的定義方式，但每種定義彼此間都是等價的，其中，域的( )函數(shù)的階FRFT的1種定義形式為：

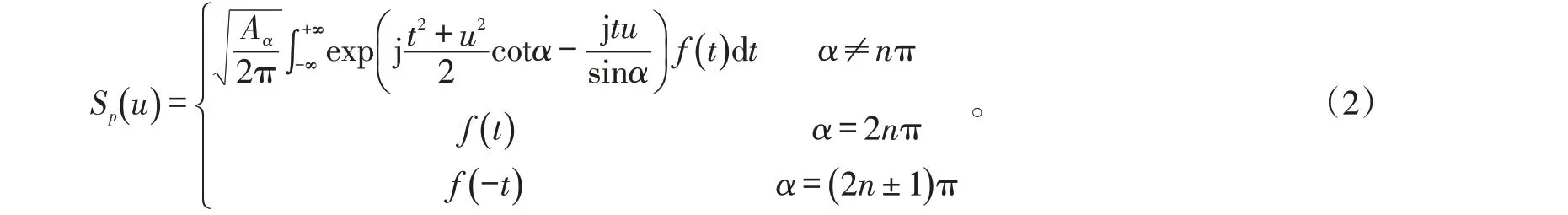
式（2）中，F(xiàn)RFT是以或為參數(shù)定義的，因此，域也稱為FRFT 域。階的FRFT 域是在()平面上按逆時針方向旋轉(zhuǎn)角度所產(chǎn)生的坐標空間。式（1）的定義中，取值范圍較廣，但由FRFT 的性質(zhì)可知，一般只需在按逆時針方向旋轉(zhuǎn)的0 ～π 2 角度范圍內(nèi)分析即可。由于FRFT 的對稱性和周期性，其他角度的信號分析結(jié)果與0 ～π 2 的旋轉(zhuǎn)角度相一致，因此，分析時，一般只需取0 ～1。當=0 時，F(xiàn)RFT 就是原函數(shù)，=1 時是普通的傅里葉變換。從0變到1，信號平滑地從原時域變到頻域，F(xiàn)RFT以連續(xù)的參數(shù)內(nèi)插在原函數(shù)和其普通傅里葉變換之間，能表征出信號從時域逐步變化到頻域的所有特性。與WT 一樣具有良好的時頻局部化特性，很適合時變信號的處理和特征提取。

1.2 算法描述

電路故障時，其響應(yīng)信號常含有非平穩(wěn)信號，其時頻域特征隨著時間變化，電路中某些元器件故障常引起響應(yīng)信號各頻率成分的能量變化。由于FRFT具有非平穩(wěn)信號的表示能力，且同一信號在不同的FRFT 域中可表現(xiàn)出不同的時頻局部能力，信號能量也表現(xiàn)出不同的時頻聚集性。因此，可以利用FRFT，使值從0連續(xù)變化到1，信號能量譜將呈現(xiàn)不同的時頻聚集性，從而刻畫出信號的局部細節(jié)變化情況。據(jù)此，本文提出1種基于FRFT域的能量譜峰值局部特征提取方法。

基本原理如下：電路發(fā)生故障時，其響應(yīng)信號往往會發(fā)生變化，有時在時域或頻域中其可分性差、特征差異并不明顯，特別是當電路發(fā)生“軟”故障且電路存在容差時，其不同故障的特征信息重疊嚴重，更不易分辨。本文提出采用將各故障狀態(tài)下（以下如無特別說明均包含正常狀態(tài)）的響應(yīng)信號映射到所有FRFT域中（值遍歷0到1），然后，取相應(yīng)FRFT域中的能量譜峰值作為信號局部化特征的反映。由FRFT的性質(zhì)，信號在某一FRFT 域中必然存在相應(yīng)的能量峰值點，而不同信號在同一FRFT 域中的能量譜峰值將會發(fā)生變化，因此，可以利用故障響應(yīng)信號在所有FRFT 域的能量譜峰值構(gòu)成故障特征，建立故障特征庫，實現(xiàn)故障診斷。然而，在實際的計算中，不可能計算連續(xù)階FRFT域的所有能量譜峰值，但由FRFT的性質(zhì)可知，在軸上，值的微小變化僅引起S()的微小變化，因此，我們可以將∈[01] 均勻地劃分為若干個區(qū)段，計算相應(yīng)值下的FRFT能量譜峰值，構(gòu)成特征向量。為了兼顧特征提取精度和計算量，需要選取合適的劃分區(qū)段值。

基于FRFT 域的能量譜峰值故障特征提取算法，步驟如下。

特征提取流程圖，如圖1所示。

圖1 基于FRFT域的能量譜峰值特征提取流程圖Fig.1 Flow chart of feature extraction based on the peak of energy spectrum in FRFT domain

1.3 算法的時間復(fù)雜度分析

本文算法的時間復(fù)雜度主要由1.2節(jié)中的步驟2）決定。由文獻[23]可知，單個信號的1次FRFT的時間復(fù)雜度為(log)，為樣本的維度。于是可得單個信號的區(qū)段全部FRFT 的時間復(fù)雜度為(log)。因此，對于樣本個數(shù)為的數(shù)據(jù)集，本文算法的時間復(fù)雜度為(log)。通常情況下，對FRFT域變換的值在[01] 之間的分段相對于樣本維度和樣本個數(shù)都較小，所以，本文算法的時間復(fù)雜度可近似為(log)。

文獻[18][20]在某一FRFT 域中計算分形維數(shù)和信息熵都可采用“盒子法”，它們的時間復(fù)雜度最小為(log)，因此，文獻[18][20]的總時間復(fù)雜度為((+1)log)，亦近似為(log)。而文獻[14]基于類內(nèi)和類間距離，利用遺傳算法搜索最優(yōu)FRFT 的故障特征提取方法的單次搜索時間復(fù)雜度為(log+)，其中，(log)代表FRFT 的時間復(fù)雜度，()是計算數(shù)據(jù)集中任意2 個樣本之間歐氏距離的時間復(fù)雜度。對于種群個數(shù)為，最大遺傳代數(shù)為的搜索過程，考慮在最壞情況下，文獻[14]的算法時間復(fù)雜度為((log+))。由此可見，本文算法時間復(fù)雜度最小，文獻[18][20]次之，都低于文獻[14]或[21]算法的時間復(fù)雜度。

2 仿真電路實驗

2.1 電路模型、參數(shù)及故障仿真設(shè)置

以兩級四運放低通濾波器電路（two-stage fouroperational-amplifier biquad low-pass filter，TSLPF）

為例進行分析驗證。該電路原理圖及其標稱值，如圖2 所示。圖中，電阻單位為Ω，電容單位為F，輸入為，輸出為。仿真過程中，設(shè)定電路中電容正常容差為10%，電阻正常容差為5%。參照文獻[8]，假設(shè)電路中的典型故障元件為～，、，～、～、、和，15種“軟”故障的詳細情況，如表1所示。

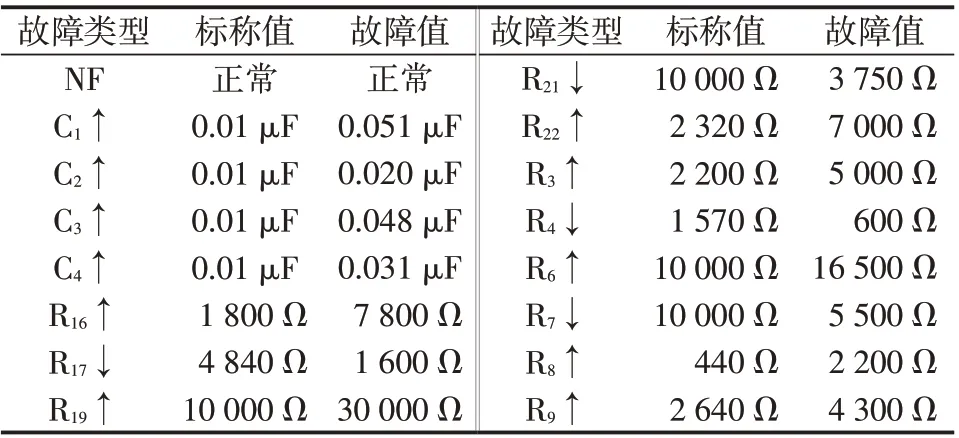
表1 TSLPF“軟”故障模式Tab.1 Soft fault modes in TSLPF circuit

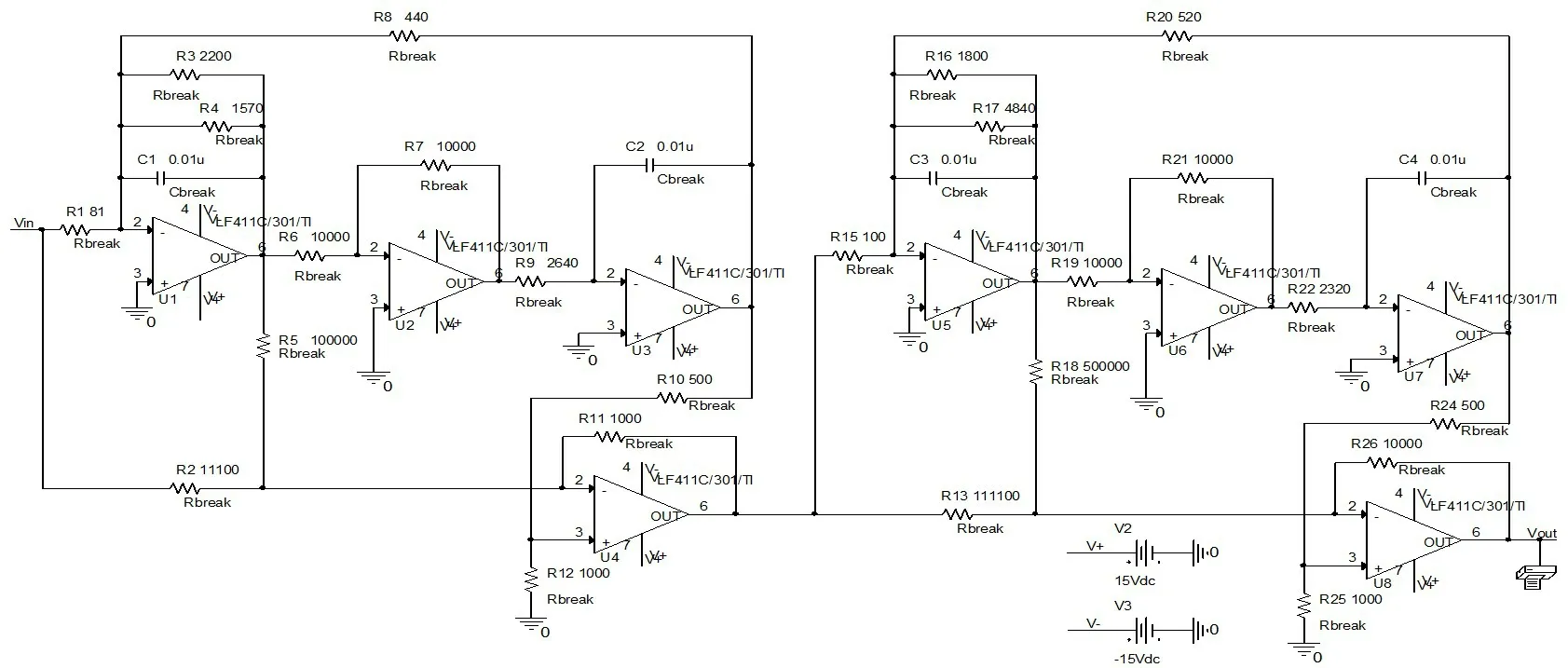
圖2 TSLPF電路Fig.2 TSLPF circuit

2.2 仿真實驗與分析

根據(jù)表1，分別對電路的各種故障狀態(tài)進行仿真，實驗中每次只設(shè)置1個故障值（Monte-Carlo隨機），其余元器件在其容差范圍內(nèi)變化。給電路施加電壓為5 V、寬度為10 μs的脈沖激勵，對電路進行瞬態(tài)分析，設(shè)置PSpice 運行時間為400 μs，采樣率為500 K/s，每種故障狀態(tài)進行50 次Monte-Carlo 分析，采樣800 組數(shù)據(jù)，每組數(shù)據(jù)201 個采樣點。各種故障狀態(tài)下的部分輸出波形，如圖3所示。上述各種故障狀態(tài)下，5個樣本利用本文方法提取的電路歸一化能量譜峰值特征（對∈[0，1]進行了21區(qū)段劃分），如圖4所示。

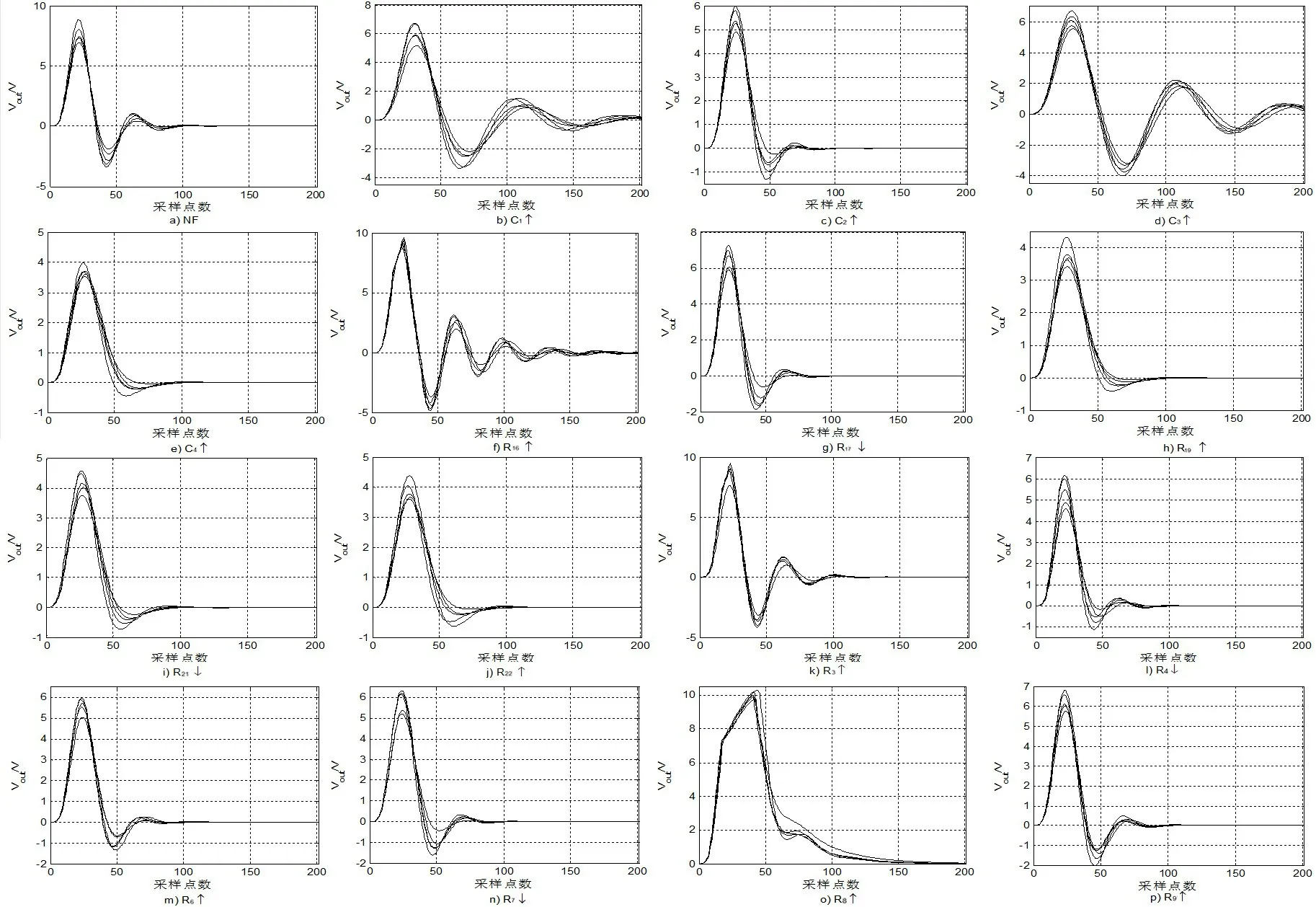
圖3 TSLPF電路各種故障狀態(tài)下的脈沖響應(yīng)Fig.3 Impulse response of TSLPF circuit under different fault status

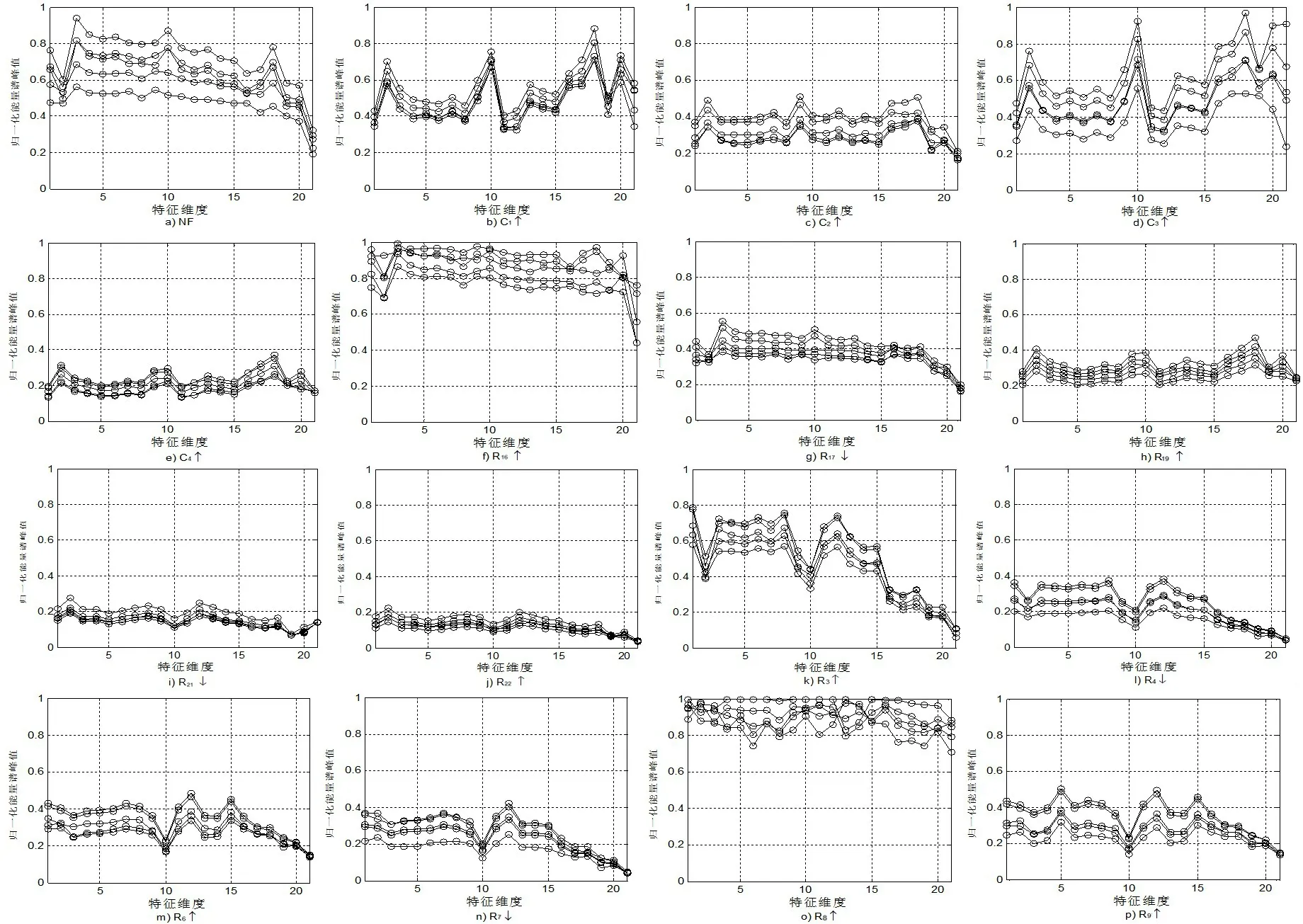
圖4 TSLPF電路各種故障狀態(tài)下的歸一化能量譜峰值Fig.4 Normalized peak of energy spectrum of TSLPF circuit under different fault status

特征向量的好壞主要看其用于故障分類時取得的診斷精度，因此，本文采用最近鄰分類器對每種方法提取的故障診斷特征進行分類測試對比。實驗數(shù)據(jù)采用隨機抽取的方法，其中，30 組數(shù)據(jù)用于訓練分類器，20 組數(shù)據(jù)用于測試分類器，且每次實驗均重復(fù)10次，計算其平均分類精度。表2記錄了文獻[14][18][20]和本文方法提取的特征向量取得的分類精度。須要指出的是，由于文獻[14][18][20]中已經(jīng)給出基于FRFT的故障特征提取方法與時域、頻域、傳統(tǒng)時頻域特征提取方法的比較結(jié)果，并一致驗證了其特征提取的結(jié)果要優(yōu)于上述相關(guān)算法，因此，本文只作FRFT方法的比較。

表2 各種算法TSLPF電路的故障診斷精度Tab.2 Fault diagnosis accuracies of TSLPF circuit based on different feature extraction algorithms

表3同時還給出了本文方法對上述800組數(shù)據(jù)進行特征提取的平均運行時間并與文獻[14][18][20]算法進行了比較。

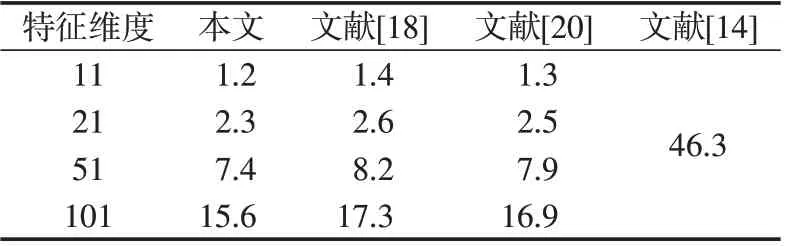
表3 各算法的平均運行時間Tab.3 Average run-time of different algorithms單位：s

實驗中，將文獻[14]算法中遺傳算法初始種群個數(shù)設(shè)置為10，最大遺傳代數(shù)設(shè)置為20，在0 ～1之間進行搜索。所有特征提取算法均使用MATLAB 2014b進行編程，程序運行在處理器為Intel（R）Core（TM）i7-6700 CPU@3.40 GHz、內(nèi)存為8 G的計算機上，操作系統(tǒng)為Windows 7。

通過圖3、4和表2、3可以得到以下結(jié)論。

1）與直接采樣原始數(shù)據(jù)相比，本文方法提取的故障特征向量使相同故障模式之間的聚集性更好，而不同故障模式之間仍然保持了一定的可分度（如圖3 和圖4）。

2）大部分故障模式的分類診斷實驗結(jié)果表明，與文獻[14]算法相比，本文方法不僅可行，還能有效改善故障特征的可分性，提高故障診斷精度。例如，對于電路中最難診斷的↑、↓和↑故障，使用本文方法均取得了91%以上的診斷率（見表2），遠遠高于文獻[14]算法，與文獻[18][20]算法取得結(jié)果相當，甚至在某些故障模式下更優(yōu)。因此，驗證了本文方法的有效性。

3）通過表3可以看出，本文方法與文獻[18][20]算法都可以通過靈活調(diào)節(jié)值的細分程度來調(diào)節(jié)特征的維度，而文獻[14]算法取得的原始特征維數(shù)只能是固定的，即為采樣點數(shù)；本文方法只在21 維的情況下就取得了優(yōu)于文獻[14]算法的201維特征。

4）對于算法的執(zhí)行效率，從表3 可以看出，其運行時間與1.3 節(jié)的理論分析結(jié)果基本一致，在所有的特征提取維數(shù)和不同算法中，本文方法效率都是最好的，明顯優(yōu)于文獻[14]算法。同時，在保證診斷率的情況下，運行時間要比文獻[18][20]算法更少，這對大規(guī)模電路故障特征提取來說是非常重要的。但同時，也應(yīng)該注意到，隨著特征提取維度的增加，本文方法與文獻[18][20]算法的運行時間也相應(yīng)地成倍增加，這些結(jié)論均與1.3節(jié)的理論分析相一致。

3 物理實驗

3.1 電路模型、參數(shù)及故障設(shè)置

現(xiàn)采用實際物理電路對本文方法進行驗證，實驗采用Sallen-Key 帶通濾波器電路，它是1 個被眾多文獻以相關(guān)方法驗證過的標準電路之一，其電路拓撲結(jié)構(gòu)及元件標稱值，如圖5 所示。制作的面包板實驗板，如圖6所示。

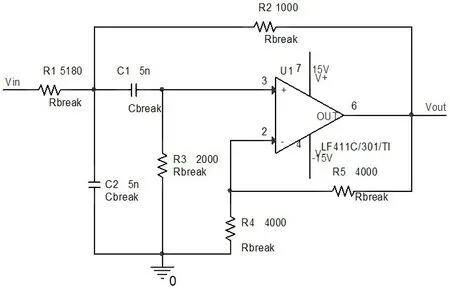
圖5 Sallen-Key原理電路圖Fig.5 Schematic diagram of Sallen-Key circuit

圖6 Sallen-Key電路的面包板實驗圖Fig.6 Breadboard experiment diagram of Sallen-Key circuit

在仿真環(huán)境中，PSpice 能夠在元件的正常容差范圍內(nèi)隨意改變其標稱值，但對于實際的物理電路來說，因為需要不斷地替換元件或在元件的容差范圍內(nèi)手動調(diào)整參數(shù)值，倘若仿照仿真程序采集所有條件下的故障數(shù)據(jù)，其工作量將是非常巨大的。另外，受實驗條件所限，對于實際電路，本文僅使用3個可調(diào)電阻來考察元件容差的影響，且電路中5 nF 電容以4.7 nF電容代替，故障時2.5 nF 電容以2.7 nF 電容代替。正常狀態(tài)下的元件值被隨機地設(shè)置在容差范圍內(nèi)。電路故障模式與文獻[8]一致，如表4所示。

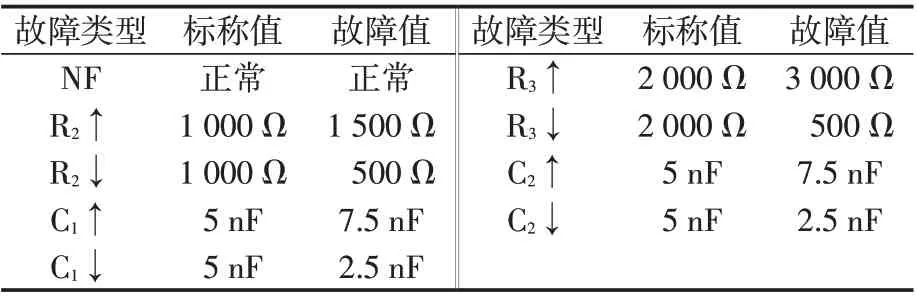
表4 實際Sallen-Key電路故障模式Tab.4 Fault modes of actual Sallen-Key circuit

3.2 電路數(shù)據(jù)采集

實際電路數(shù)據(jù)采集時，測試激勵為5 V、10 μs 的方波脈沖信號，采用Tektronix公司的任意函數(shù)發(fā)生器（AFG3102）產(chǎn)生，測試輸入為。利用北京科瑞興業(yè)科技有限公司的KPCI-1817卡采集節(jié)點的輸出電壓信號并進行保存，設(shè)置為單次采樣，且采樣率為500 K/s，采用半滿中斷，每次采樣1 024 個點，并根據(jù)實際情況取前181個點作故障分析。由于在采樣的過程中，板卡和函數(shù)發(fā)生器之間不同步，需要在采集的數(shù)據(jù)中手動選取數(shù)據(jù)起始點，因此，考慮到工作量，本文對每類故障模式只采集10個樣本，實際電路采集的故障波形，如圖7所示（每種故障狀態(tài)隨機選擇3個樣本進行顯示）。

圖7 實際Sallen-Key電路各種故障狀態(tài)的脈沖響應(yīng)Fig.7 Impulse response of actual Sallen-Key circuit under different fault status

3.3 實驗與分析

采用本文方法對上述采集數(shù)據(jù)進行處理，圖8為采用本文方法對各故障狀態(tài)進行歸一化FRFT域能量譜峰值特征處理得到的部分結(jié)果，實驗中將FRFT值均分為11個區(qū)段。

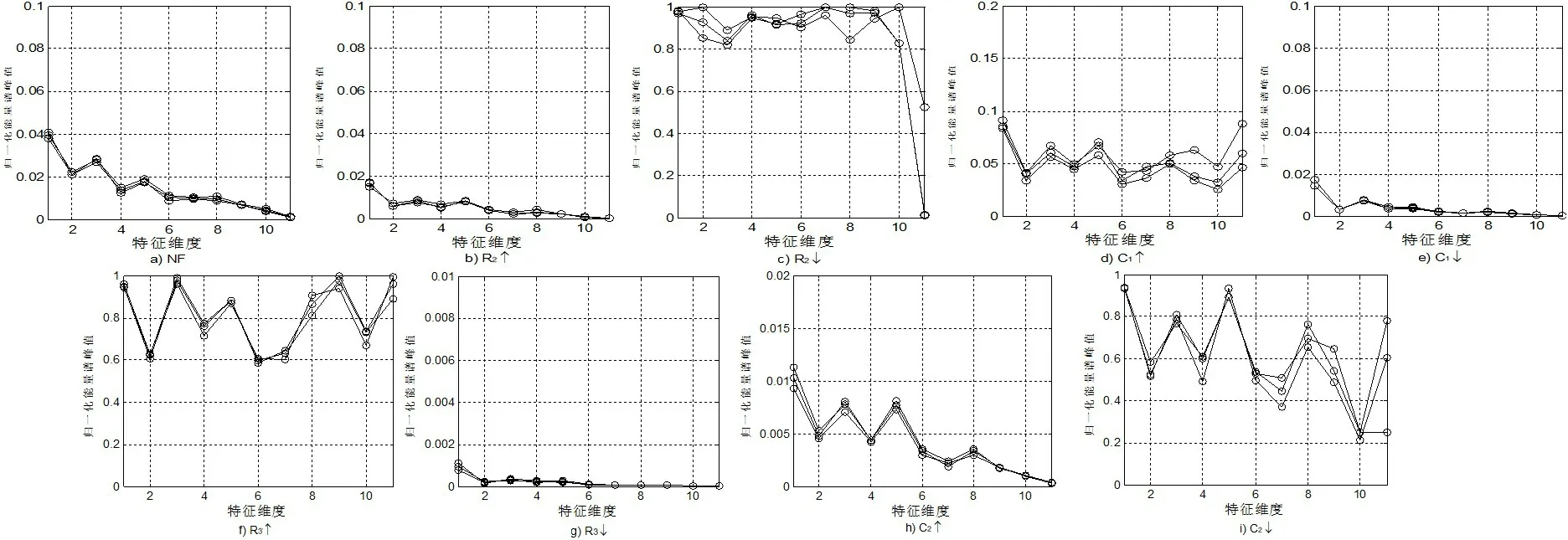
圖8 實際Sallen-Key電路各種故障狀態(tài)下的歸一化能量譜峰值Fig.8 Normalized peak of energy spectrum of actual Sallen-Key circuit under different fault status

為了更加客觀地評價不同特征提取方法的診斷性能，同樣，采用最近鄰分類器對上述取得的特征進行診斷，診斷結(jié)果，如表5 所示。仿真實驗已表明，文獻[18][20]算法與本文算法診斷精度相當，差別在于算法運行時間，但實際試驗中樣本量太少，運行時發(fā)現(xiàn)基本無異，所以沒有列出各種算法的運行時間，同時也并未在表5中列出其他算法的診斷精度。因樣本有限，在分類診斷過程中，所有的樣本既用于訓練分類器也用于測試分類器。

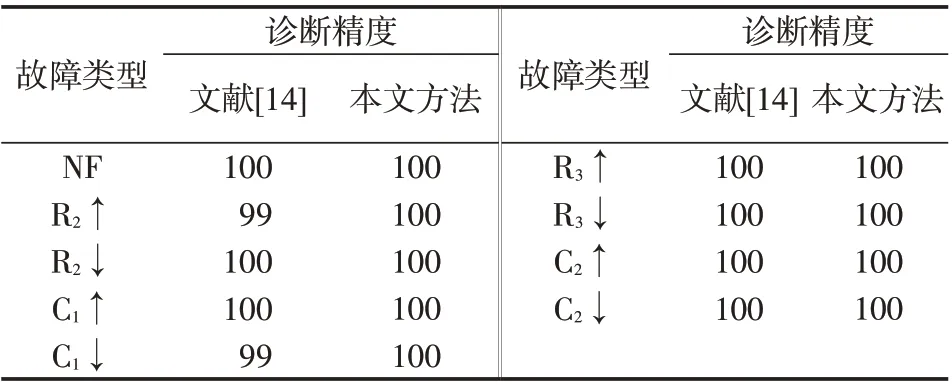
表5 各種算法的電路故障診斷精度Tab.5 Fault diagnosis accuracies based on different feature extraction algorithms

從圖7、8和表5中可以看出：

1）對于實際的電路故障診斷，由于其容差設(shè)置的限制，實際采集的數(shù)據(jù)受容差的影響有限，數(shù)據(jù)變化都較為集中，相同故障的特征有更好的聚集性，將更有利于分類；

2）特別的，對于↓故障，從原始采集的數(shù)據(jù)來看，由于此時電路構(gòu)成的線性系統(tǒng)已處于發(fā)散狀態(tài)，如圖7i），微小的容差變化導致電路的脈沖響應(yīng)變化差異較大，但本文方法取得的故障特征卻相對比較集中，如圖8i），究其原因可以認為，對于↓故障，其造成的FRFT域能量變化規(guī)律是一致的，因此，其取得特征的一致性也較好；

3）本文方法對于所有故障的診斷均取得了100%的正確率，與文獻[24]的最好診斷結(jié)果一致，但文獻[14]算法卻在↑和↓故障上出現(xiàn)了“誤診”，其故障診斷率只有99%，因此，使用本文方法得到的特征樣本確實能有效提高模擬電路的故障診斷率。

4 結(jié)論

針對模擬電路的故障診斷問題，為提高故障特征的可診性，本文提出1種基于FRFT域能量譜峰值的特征提取方法。該方法是基于不同信號在不同F(xiàn)RFT域的時頻聚集性將發(fā)生變化，通過提取不同F(xiàn)RFT 域的局部信息來區(qū)分故障的。采用仿真和物理電路驗證了該方法的有效性，并與其他相關(guān)方法進行了性能對比。結(jié)果表明，本文方法能夠在所有FRFT 域中更全面地獲取不同故障響應(yīng)信號的細微差異，有利于提高故障特征的可分性，同時，算法時間復(fù)雜度也有明顯改善。雖然本文方法提高了特征的可分性，但隨之而來的問題卻是值的細分程度問題，同時，如何對特征維度進行優(yōu)化也是1個有待研究的問題。