Q-learning強化學習協同攔截制導律

王金強，蘇日新，劉 莉，劉玉祥，龍永松

(江南機電設計研究所，貴陽 550025)

0 引言

隨著飛行器技術的不斷發展，現代戰爭呈現出智能化、信息化、多樣化的特點，體系與體系的對抗將貫穿戰爭始終，尤其是以精確制導武器為主的攻擊體系和以地空艦導彈為主的防御體系之間的對抗，在上述情況下，傳統的單導彈作戰模式已難以滿足實際作戰需求。彈群協同作戰是將所有參戰導彈組成一個作戰網絡，在指揮中心的調控下，實現彈間信息通信和共享，具有更高的作戰效能，是未來智能導彈的重點發展方向。

I.Jeon等在制導律設計中引入時間約束，提出了一種可變攻擊時間的協同制導律，并通過數值仿真驗證了算法的有效性。Chen Y. 等在時間控制的基礎上，進一步考慮了存在末端攻擊角度約束的情況。李強針對協同制導問題，分別在視線方向和視線法向設計了有限時間收斂滑模制導律。H. B. Oza等為提高運算效率，設計了考慮末端多約束的模型預測靜態規劃制導律。Liu X. 等為處理制導過程中存在的不確定性，基于李雅普諾夫穩定性理論，提出了一種自適應滑模協同制導律，但該方法存在系統抖振的問題。宋俊紅等基于超螺旋滑模控制算法，設計了一種雙層協同制導律，有效改善了制導控制系統的暫態特性。肖惟等研究了多枚過載受限的弱機動導彈攔截強機動目標的協同攔截問題，提出了基于標準彈道的分布式協同攔截策略設計方法。Zhai C. 等為提高協同攔截的成功率，設計了一種基于覆蓋的攔截算法。雖然上述算法具有良好的控制效果，但在設計過程中均需預先指定期望攻擊時間，各枚導彈間沒有信息交互，并沒有實現真正意義的智能協同作戰。

隨著人工智能領域的迅猛發展，強化學習算法作為一種智能決策算法，在導彈制導控制、智能任務規劃和故障診斷等方面取得了顯著成果。B. Gaudet等為提高制導律魯棒性，基于神經網絡設計了一種強化元學習制導律。張秦浩等基于Q-learn-ing強化學習算法設計了最優攔截制導律。南英等則對傳統Q網絡進行改進，提出了一種基于Markov決策過程的制導律，且不需要訓練樣本，可自主搜索獎勵值最大的動作并完成訓練。陳中原等提出了一種基于深度確定性策略梯度的強化學習協同制導律，引入Actor和Critic網絡選取動作和獎勵值的逼近。上述算法雖然使導彈具有自主決策能力，但運算量大，現有的彈載計算機難以滿足要求。

為解決上述問題，本文以傳統比例制導律為基礎，引入智能決策，提出了一種Q-learning強化學習協同攔截制導律，并通過數值仿真驗證了算法的有效性和優越性。

1 協同攔截模型

圖1給出了導彈平面攔截幾何，其中為慣性系，M和T分別代表導彈和目標，表示速度，表示彈道傾角，表示視線角，表示前置角，表示法向角速度，表示彈目相對距離。

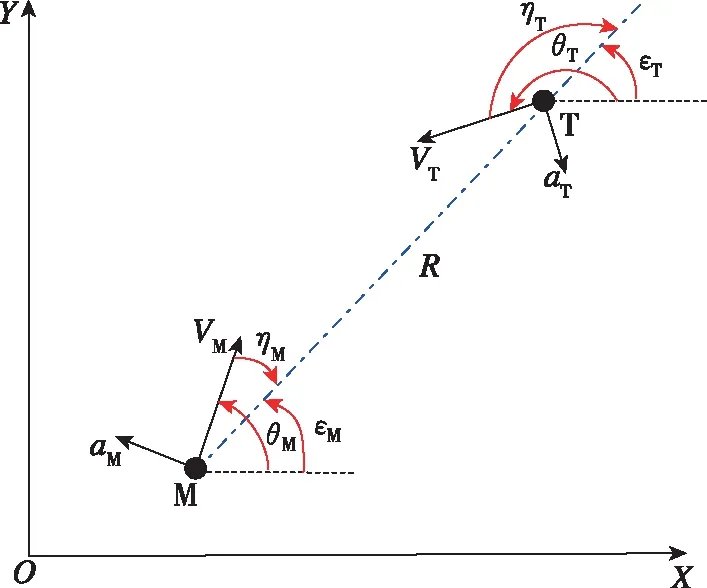
圖1 導彈攔截平面幾何Fig.1 Planar interception geometry of missile

基于坐標轉換得到導彈與目標的非線性相對運動方程為

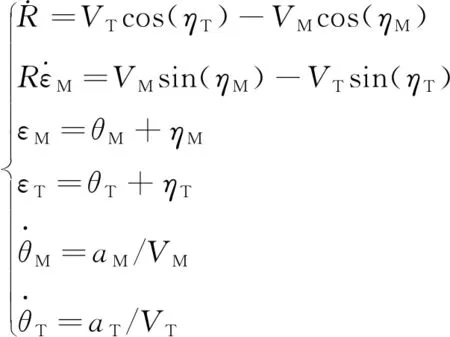
(1)

隨后，建立導彈非線性協同攔截模型，其示意圖如圖2所示，其中M,表示第枚導彈的最大機動區域，為目標的最大機動逃逸區域，記為逃逸域，為導彈最大機動過載，表示目標的逃逸加速度，定義為=+，其中為標準攔截彈道下目標期望逃逸加速度，為小量，且||越大，攔截彈道越彎曲。為簡化非線性模型，便于數學處理，此處假設為常值。因此，基于文獻[16]中標準彈道的思想和逃逸域理論，彈群協同攔截模型的構建過程如下：

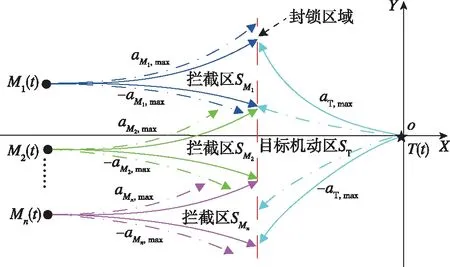
圖2 彈群協同攔截策略Fig.2 Cooperative interception strategy of multiple missiles

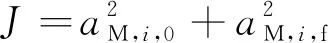
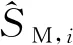
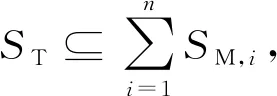
2 協同攔截制導律

本章將結合Q-learning強化學習算法進行協同制導律設計。首先，基于標準彈道的思想，以導彈的最大機動區域M,中的標準彈道攔截機動的目標，以非標準彈道攔截+機動的目標，則協同制導律M,可設計為

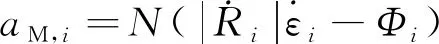
(2)

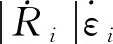
隨后，定義導彈與目標飛行過程中的零控脫靶量為

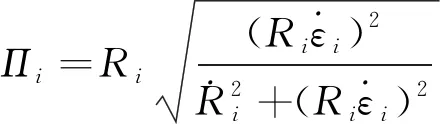
(3)

同理，導彈以標準彈道攔截機動目標過程中的零控脫靶量,s定義為

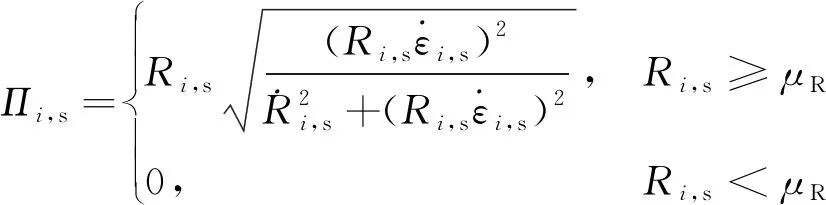
(4)

式中，為一個小量，且>0，用于避免求解式(5)中,s,,s和M,,s時發生奇異。

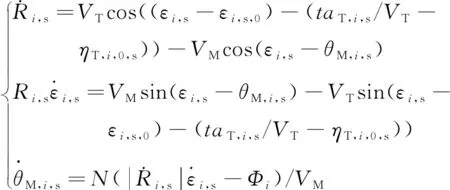
(5)

則偏置項自適應調節律可設為

(+1)=

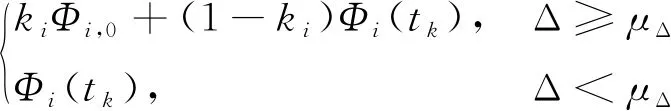
(6)

式中，,0為預先設定偏置項；為偏置系數，定義為=exp(-,s)；為一個小量，且>0，Δ=exp(-,s)。

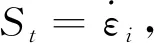
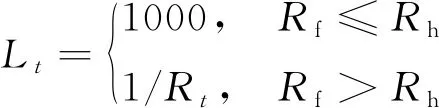
(7)

式中，為導彈終止時刻彈目相對距離；為導彈命中目標所需最小彈目距離，常取=1，即表示在攔截過程中，獎勵值隨彈目距離的減小而增大，若最終命中目標，則得到一個更大的獎勵，若沒有命中目標則獎勵值為0。

綜上，基于Q-learning強化學習算法的目標策略設為

(,)]+(,)

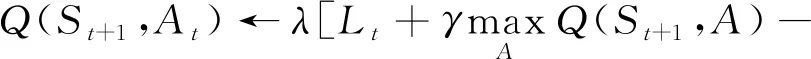
(8)

行為策略為-greedy策略，即

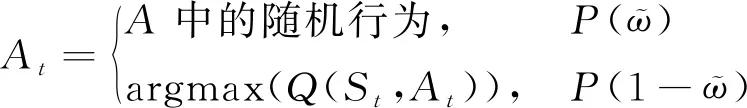
(9)

式中，為學習效率參數；為折扣率參數；?為策略參數，即導彈以?的概率在動作空間中進行隨機選擇，則以1-?的概率會選擇得到最大值的動作。Q-learning強化學習算法流程如圖3所示。

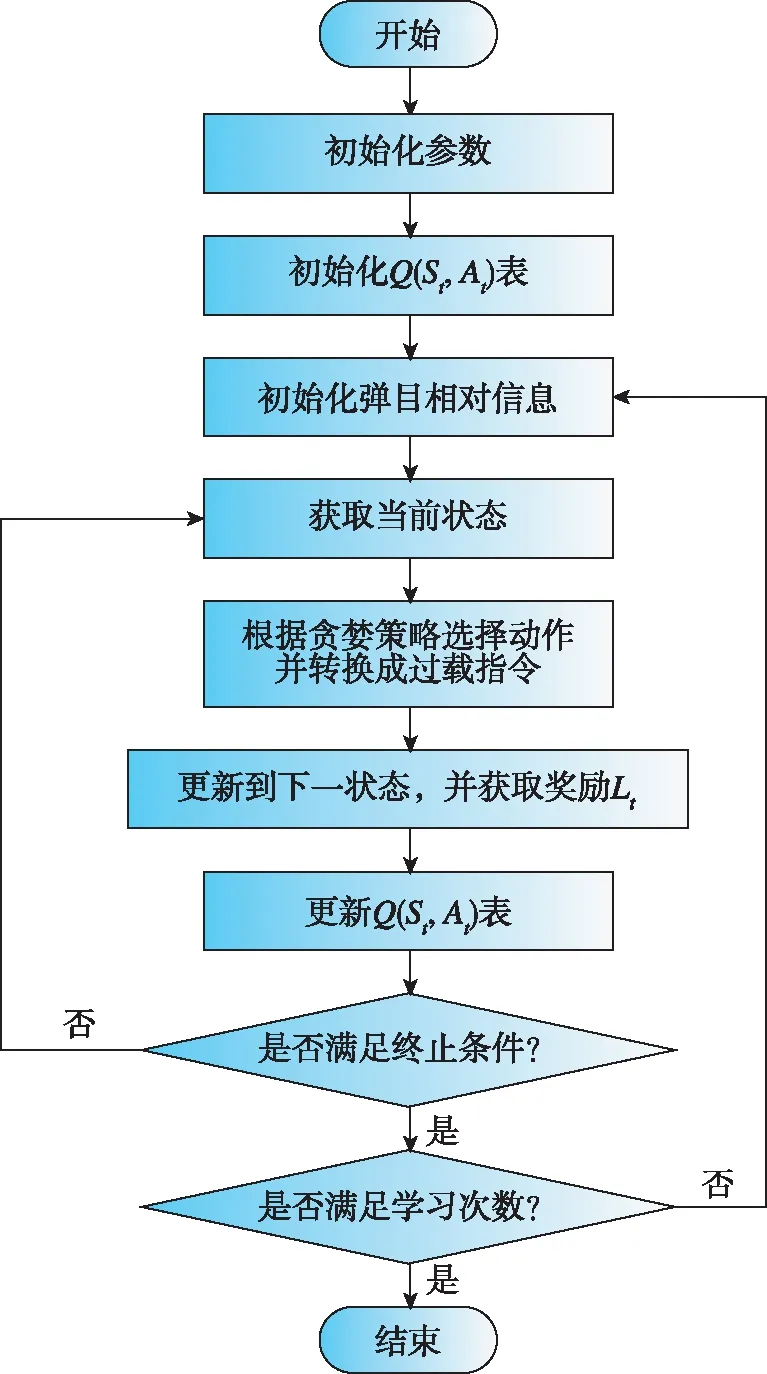
圖3 Q-learning強化學習算法流程Fig.3 Flow chart of Q-learning algorithm

3 攔截區域分配

本章基于逃逸域覆蓋理論進行多彈攔截區域分配算法設計。為方便推導，定義歸一化的目標加速度為=，導彈覆蓋區域M,和目標逃逸域可分別歸一化為[,low,,up]和[-1，1]。

所設計攔截區域分配策略如圖4所示，導彈1的攔截區域左邊界與目標逃逸域左邊界對齊，導彈攔截區域M,右邊界與目標逃逸域右邊界對齊，每枚導彈覆蓋范圍相同。

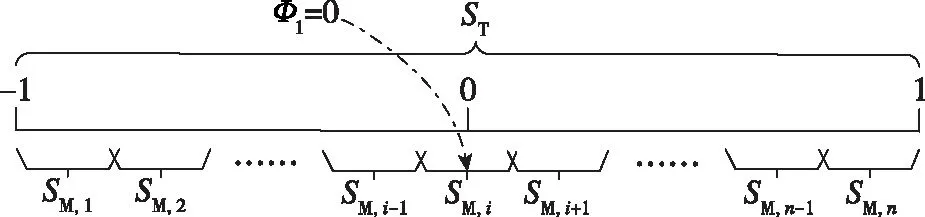
圖4 攔截區域分配模式Fig.4 Allocation modes of intercept area

為實現上述分配策略，首先求解個導彈的攔截區域{M,|=1,2,3,…,}，其中的左邊界與-1對齊，M,的右邊界與1對齊，M,-1和M,不重疊相接，M,-1與M,可重疊相交，即=-1，,up=1，-1,up=,low，-1,up-,low≥0。同時，為使每枚導彈攔截覆蓋區域均勻分布，此處將重疊區域[,low,-1,up]均勻分配到其余子區域上，即將覆蓋區域～M,-1分別向左移動(-1)(-1)× (-1,up-,low)長度，算法具體偽代碼如表1所示。

表1 攔截區域分配的實現算法

4 數值仿真分析

本章分別針對多彈齊射(模式1)和子母彈分離發射(模式2)兩種作戰模式，對上述協同制導律的有效性進行數值仿真驗證。在多彈齊射作戰模式下，假設導彈速度方向與軸線重合，即攻角、側滑角和前置角均為0，因此其初始陣位約束為

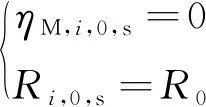
(10)

子母彈分離作戰模式下，忽略子彈和母彈間的動態過程，并假設初始時刻目標前置角和彈目的距離相同，因此其初始陣位約束為

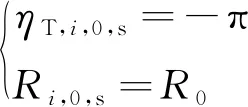
(11)

仿真環境下假設導彈數目為3，分別記為、和，彈目初始相對距離設為60km，導彈速度為7，最大機動過載3，目標速度為6，最大機動過載5，有效導航比由Q-learning算法在線計算，學習率參數設為0.01，折扣率參數則設為0.99。

針對目標最大正機動(=1)、不機動(=0)和最大負機動(=-1)的協同攔截仿真結果如圖5～圖10所示。圖5和圖7所示分別為兩種作戰模式下的攔截軌跡，從中可知，針對上述三種目標機動形式，本文所提協同制導律可確保至少有一枚導彈成功命中目標，證明了算法的有效性。圖6和圖8所示分別為兩種作戰模式下的導彈過載曲線。圖9和圖10所示分別為導彈1最大負機動(=-1)條件下的有效導航比曲線和均值曲線，從中可知，在制導過程中有效導航比可進行自適應調節，且隨著訓練的進行，均值逐漸收斂。

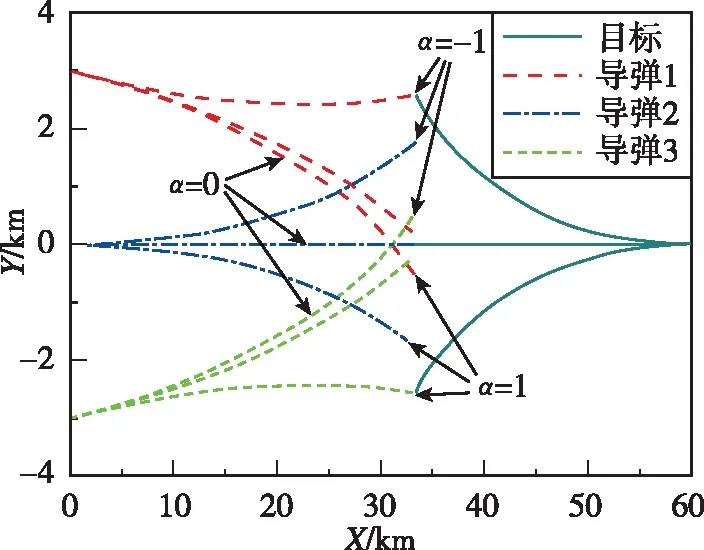
圖5 作戰模式1的攔截彈道Fig.5 Interception trajectory under mode 1

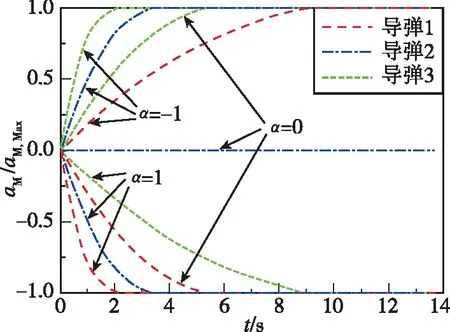
圖6 作戰模式1的導彈過載Fig.6 Acceleration of missile under mode 1

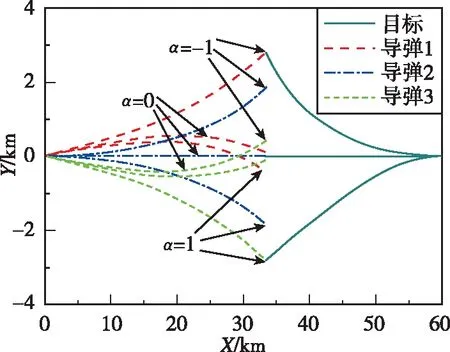
圖7 作戰模式2的攔截彈道Fig.7 Interception trajectory under mode 2

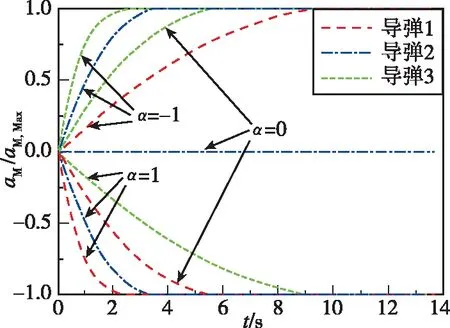
圖8 作戰模式2的導彈過載Fig.8 Acceleration of missile under mode 2

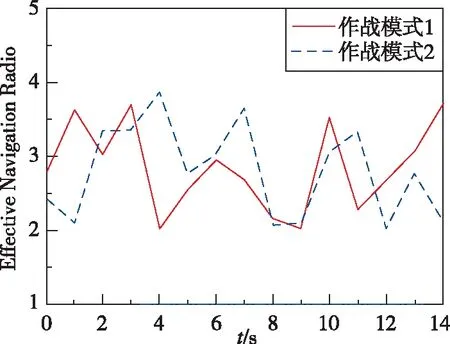
圖9 有效導航比N曲線Fig.9 Curve of effective navigation ratio N

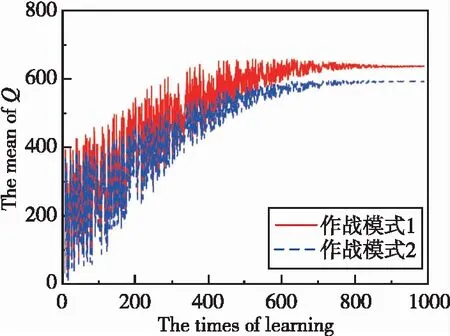
圖10 Q均值收斂曲線Fig.10 Convergence curve of the mean of Q

針對目標做=-sign(sin(π/2))蛇形機動的仿真結果如圖11～圖14所示。圖11和圖12所示分別為兩種作戰模式下的攔截軌跡，從中可知，引入偏置項可使導彈在攔截過程中更加接近目標，有效提升了攔截效果。圖13和圖14所示為零控脫靶量曲線，可以看出，與傳統比例制導律相比，本文設計的協同制導律零控脫靶量更低，具有更強的工程實用價值。

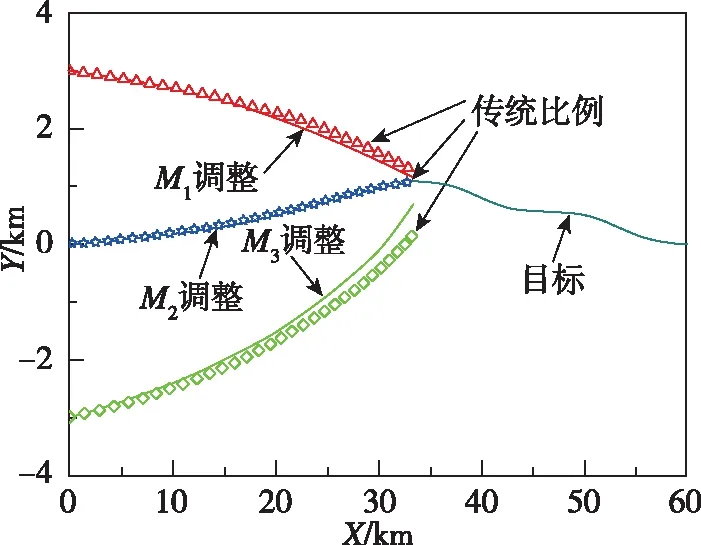
圖11 作戰模式1的攔截彈道Fig.11 Interception trajectory under mode 1

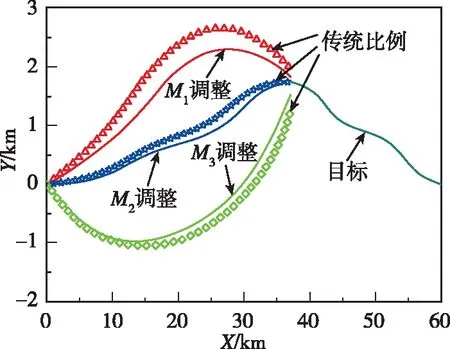
圖12 作戰模式2的攔截彈道Fig.12 Interception trajectory under mode 2

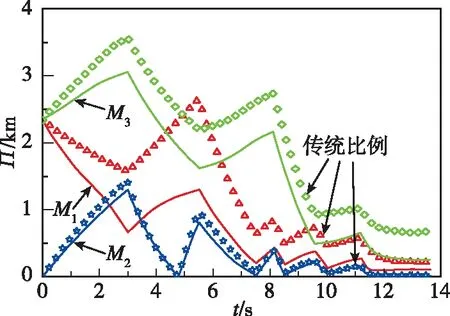
圖13 作戰模式1的零控脫靶量Fig.13 Zero effort miss under mode 1

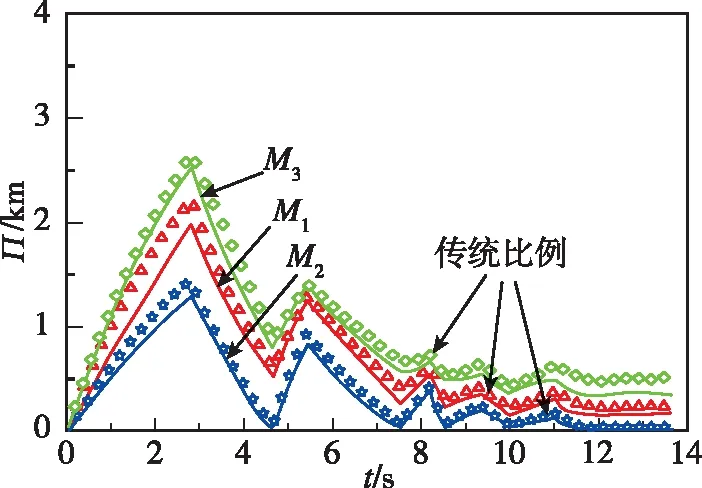
圖14 作戰模式2的零控脫靶量Fig.14 Zero effort miss under mode 2

5 結論

本文研究了多彈協同攔截機動目標問題，具體結論如下：

1)基于逃逸域覆蓋理論、比例制導律和Q-learning算法提出了一種強化學習協同制導律。

2)針對多彈齊射和子母彈分離發射兩種作戰模式進行了數值仿真，結果驗證了所提算法的有效性和優越性。

3)后續工作可進一步研究三維空間中存在攻擊角約束、能量約束、避障和避撞等因素的協同攔截問題，為實現多約束條件下的智能協同制導奠定基礎。