廣義二維多項式混沌映射及其在信息傳輸中的應用

閆文浩，姜子敬，黃欣，朱淑娟，丁群

（1.黑龍江大學電子工程學院，黑龍江 哈爾濱 150080；2.澳大利亞佛林德斯大學科學與工程學院，通斯利 SA 5042）

0 引言

非線性動力系統(tǒng)在許多研究領域都受到越來越多的關注[1-2]。混沌映射是一種典型的非線性映射，其具有初值敏感性、內稟隨機性、遍歷性、拓撲傳遞性和正的Lyapunov 指數(shù)等優(yōu)良特性[3-5]。這些特性使混沌映射更適用于密碼學、信號處理、神經網絡等領域[6-9]。

現(xiàn)有混沌映射在工程應用中存在許多缺點。1)由于經典混沌映射結構比較簡單，隨著計算機計算能力的提升，混沌映射的控制參數(shù)，甚至整個序列都可以被估計出來。2) 這些混沌映射都存在弱混沌現(xiàn)象，即控制參數(shù)發(fā)生微小的變化，就會造成混沌現(xiàn)象的消失。3) 由于動力學退化的問題，這些混沌映射會產生嚴重的安全缺陷，從而影響基于混沌的應用[10-11]。

為了改善混沌映射的動力學特性，許多新的混沌映射被提出。新的混沌映射大致分為兩類，第一類是基于現(xiàn)有混沌映射提出的改進混沌映射，文獻[12]提出了離散憶阻器模型耦合一維混沌映射，得到了新的二維混沌映射，文獻[13]提出了將3個不同的一維映射嵌套生成分段函數(shù)，文獻[14-15]將2 個一維混沌耦合生成二維混沌映射；第二類是基于線性函數(shù)或非線性函數(shù)構建新的混沌映射，文獻[16]基于“周期三蘊含混沌”提出了新的二維混沌映射并研究了該映射的動力學特性，文獻[17]提出了三維超混沌映射并基于該混沌映射提出了一個混沌傳輸方案，文獻[18]基于三維分段映射提出了一個圖像加密方案。上述研究都比較特殊，沒有一種廣義的表達式，不具有一般性。文獻[19]根據相似矩陣的觀點，提出了一個高維離散混沌映射，但該映射只針對高維混沌映射，不適用于二維混沌映射。文獻[20]根據Lyapunov 指數(shù)的定義反向構造了一個二維多項式混沌映射，基于這種構造方法，映射中的一個方程必為線性映射。如果初始值和控制參數(shù)選取特殊值，那么映射的維數(shù)就會降低，映射所產生序列的復雜度不能滿足要求。為此，本文提出一種二維多項式混沌映射，其可以產生具有穩(wěn)健性和既定復雜行為的二維混沌映射。理論仿真和實驗結果表明了該映射的優(yōu)越性。本文的主要工作總結如下。

1) 本文提出了一個廣義二維多項式混沌映射，通過一個命題給出不同控制參數(shù)和多項式最高次數(shù)，得到一系列具體的二維混沌映射。

2) 理論分析結果表明，二維多項式混沌映射可以產生穩(wěn)健混沌和期望的Lyapunov 指數(shù)。

3) 為了闡述該映射的有效性，本文給出了一個具體的數(shù)值實例，特性分析表明，本文提出的混沌映射比Hénon 映射、2D-SLM 和 2D-LSMCM 動力學特性更為復雜。

4) 本文將不同混沌映射應用于RM-DCSK 通信方案，實驗結果表明，本文映射更適合于信息傳輸。

1 二維混沌映射

本節(jié)介紹3 種典型的二維混沌映射，并通過分岔圖和相空間運動軌跡分析其動力學特性。由于現(xiàn)有映射只在一定的參數(shù)范圍內存在混沌行為，且混沌序列的輸出不均勻，本文提出了一個二維多項式混沌映射。首先，通過設計一個命題，從理論上給出了系統(tǒng)存在混沌行為的參數(shù)取值。然后，選擇不同控制參數(shù)和多項式最高次數(shù)，得到許多具有穩(wěn)健混沌和既定復雜行為的二維混沌映射。最后，通過平衡點分析研究了該映射的穩(wěn)定性。

1.1 現(xiàn)有二維混沌映射

Hénon 映射作為經典的二維離散混沌映射，其數(shù)學表達式為

其中，xn和yn為映射的狀態(tài)變量，a和b為映射的控制參數(shù)。當參數(shù)時，映射為混沌狀態(tài)。近年來，許多學者也提出了改進的二維混沌映射，文獻[14]以一維Logistic 映射和Sine 映射為基礎，提出了一種新的二維混沌映射（2D-SLM,two dimensional sine-logistic map），其數(shù)學表達式為

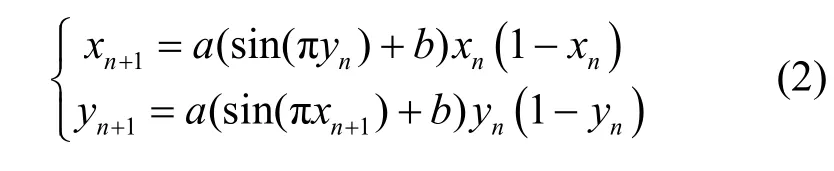
其中，xn和yn為映射的狀態(tài)變量，a和b為映射的控制參數(shù)。當參數(shù)時，映射為混沌狀態(tài)。文獻[15]同樣以一維Logistic 映射和Sine 映射為基礎，提出了另一種新的二維混沌映射（2D-LSMCM,two dimensional logistic-sine-modulated-coupling map），其數(shù)學表達式為

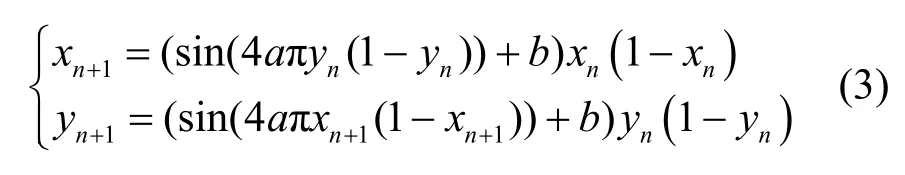
其中，xn和yn為映射的狀態(tài)變量，a和b為映射的控制參數(shù)。當參數(shù)時，映射為混沌狀態(tài)。對于一個混沌映射，其分岔圖刻畫了不同參數(shù)情況下的運動軌跡。通過分岔圖可以直觀地衡量混沌映射在不同控制參數(shù)下的遍歷性和非周期性。圖1的前兩列展示了3 個混沌映射的2 個狀態(tài)變量xn和隨控制參數(shù)b變化的分岔圖（控制參數(shù)a固定），可以看出3 個映射的分岔圖只有在很小的區(qū)域內才表現(xiàn)出混沌狀態(tài)，并且出現(xiàn)了周期窗。若控制參數(shù)發(fā)生偏差，映射就有可能從混沌態(tài)退化為周期運動。圖1 的最后一列描繪了3 個映射在固定參數(shù)下的相空間運動軌跡，可以看出Hénon 映射的輸出序列只分布在二維平面的一小塊區(qū)域，而其他映射的輸出序列也分布在特定區(qū)域。這說明3 個映射的輸出序列分布不具有均勻性，會使混沌映射在圖像加密、信息傳輸、信息安全領域受到影響。

圖1 二維混沌映射的分岔圖和運動軌跡

1.2 廣義二維多項式混沌映射

為了增強混沌映射的動力學特性，本文提出了一種二維多項式混沌映射。其數(shù)學表達式為

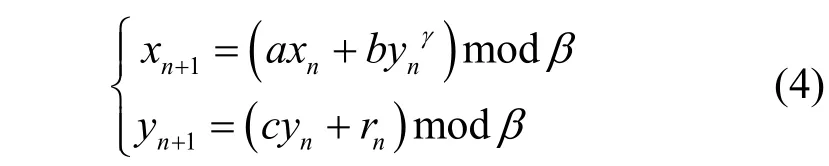
其中，xn和yn是映射的狀態(tài)變量，a,b,c,r是映射的控制參數(shù)，γ是多項式最高次數(shù)，β是取模系數(shù)。為防止狀態(tài)變量yn塌陷為一個固定值，本文將rn取為隨機擾動量。下面，通過一個命題來討論該映射何時處于混沌狀態(tài)。

1.3 混沌行為證明

Lyapunov 指數(shù)是用來證明一個映射是否為混沌最有效的手段。本文采用Lyapunov 指數(shù)來判別所構造的映射。

定義1[21]若一個二維映射是全局有界的，且至少有一個正的Lyapunov 指數(shù)，則該映射處于混沌狀態(tài)；若具有2 個正的Lyapunov 指數(shù)，則處于超混沌狀態(tài)。

一個二維離散動力學映射的2 個Lyapunov 指數(shù)計算表達式為

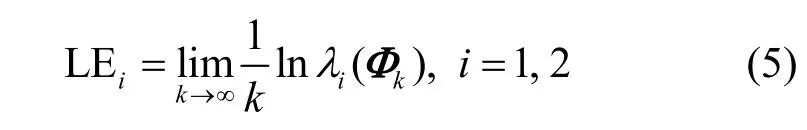
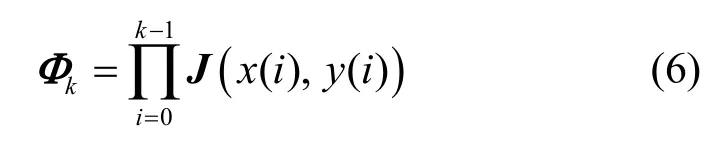
其中，J(·) 是系統(tǒng)第i次迭代時的Jacobian 矩陣。

命題1若式(4)的控制參數(shù)則該映射是混沌的。若則該映射是超混沌的。

證明式(4)第i次迭代的Jacobian 矩陣為

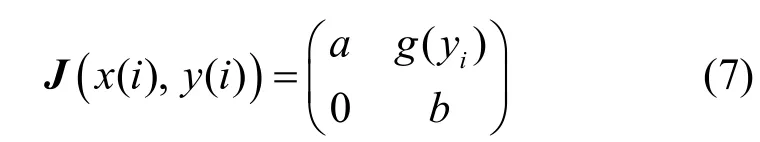
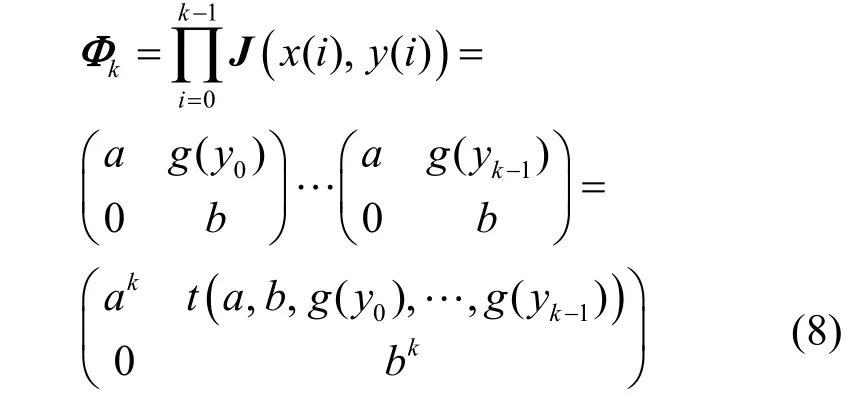
那么該映射的2 個Lyapunov 指數(shù)的推導過程為

同理，LE2=lnb。由于式(4)加入了取模運算，因此映射的輸出必定是全局有界的。若控制參數(shù)，則必有一個正的Lyapunov 指數(shù)，則該映射處于混沌狀態(tài)。若控制參數(shù)且則2 個Lyapunov 指數(shù)都是正的，則該映射處于超混沌狀態(tài)。證畢。

1.4 平衡點及穩(wěn)定性

平衡點是指動力學系統(tǒng)下一時刻的運動狀態(tài)與當前時刻的狀態(tài)一致，其數(shù)學表達式為二維混沌映射所有的平衡點都是方程式(11)的解。

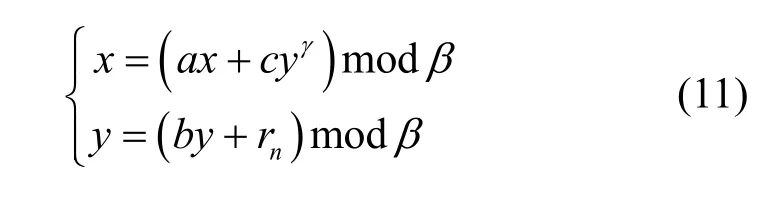
通過對式(11)進行求解，可以得到許多不同的平衡點。顯然，(0，0) 是上述方程的一個解，因為不同的參數(shù)設置，上述方程會出現(xiàn)很多非零平衡點。不妨設系統(tǒng)的非零平衡點為，混沌映射的Jacobian矩陣為式(7)。從式(7)可以看出，Jacobian 矩陣的2個特征值為λ=a，λ=b，即特征值只取決于控制參數(shù)，而與狀態(tài)變量無關。當參數(shù)a＞1 且b＞1 時，Jacobian 矩陣的2 個特征值始終為那么二維混沌映射模型所有非零平衡點都是不穩(wěn)定的，從而系統(tǒng)可以表現(xiàn)出混沌狀態(tài)甚至超混沌狀態(tài)。

2 數(shù)值實驗

本節(jié)按照命題1 給出的結論，構造了一個具體的二維多項式混沌映射。目前，判斷混沌特性的主要方法主要有相軌跡（相圖）分析法、分岔圖、Lyapunov 特征指數(shù)法、分數(shù)維分析法、復雜度測度法、自功率譜譜分析法等[22]。本文通過相圖、分岔圖、Lyapunov 指數(shù)、樣本熵（SE,sample entropy）、關聯(lián)維數(shù)（CD,correlation dimension）分析其動力學行為，并通過與現(xiàn)有二維混沌映射進行對比，以闡述該映射的優(yōu)良特性。

2.1 數(shù)值實例

為了方便計算，本文取γ=2，該二維多項式混沌映射的數(shù)學表達式為

由命題1 可知，若要使式(12)處于混沌狀態(tài)，則令a=2，b=3，c=1.7，β=1，rn是(0,1)范圍的一個隨機數(shù)。為了方便討論，本文將控制參數(shù)的范圍取為a,b,c∈(1,5)。

2.2 分岔圖與運動軌跡

對于一個混沌映射，其分岔圖刻畫了不同參數(shù)情況下的運動軌跡。通過分岔圖，可以直觀地衡量混沌映射在不同控制參數(shù)下的遍歷性和非周期性。動力學系統(tǒng)的分岔圖顯示了在不同參數(shù)下系統(tǒng)在相空間中所經過的點，為研究混沌的性質提供了一種直觀的方法。圖2 以三維視角展示了該映射隨2 個參數(shù)變化的分岔圖。從圖2 中可以看出，狀態(tài)變量xn在不同的控制參數(shù)下都均勻地分布在整個空間。圖3 展示了映射在固定參數(shù)下的運動軌跡，隨著迭代次數(shù)的增加，系統(tǒng)的輸出范圍為[0,1) 。

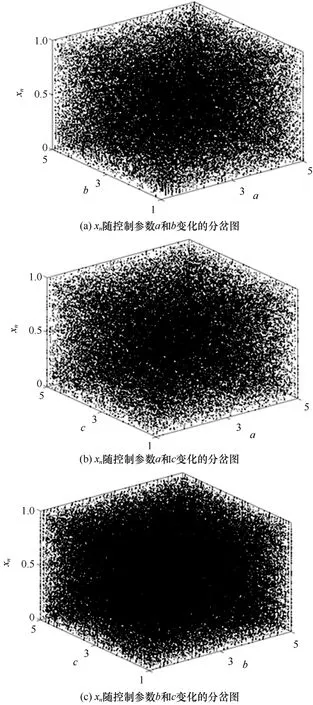
圖2 映射隨2 個參數(shù)變化的分岔圖

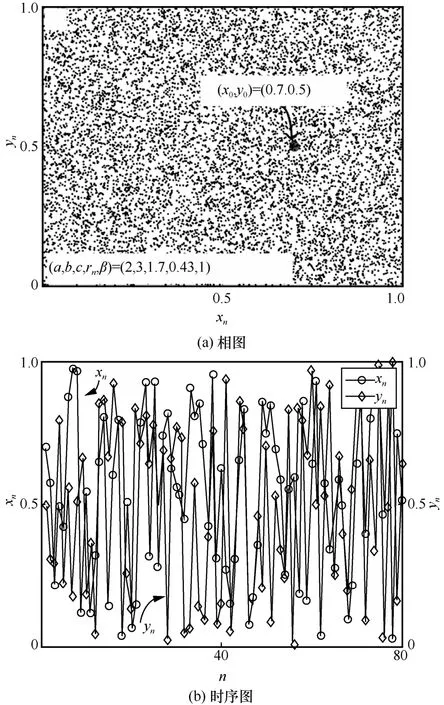
圖3 映射在固定參數(shù)下的運動軌跡

2.3 Lyapunov 指數(shù)

在非線性動力學理論中，Lyapunov 指數(shù)可有效地描述映射隨時間演化時映射對初值的敏感性。對初始條件的敏感性是混沌的一個重要特征，即相空間中的2 個軌道彼此接近，隨著時間的推移，它們會以指數(shù)形式分離。若Lyapunov指數(shù)為負，表明系統(tǒng)的相體積在運動方向上是收縮的，即該方向的運動是穩(wěn)定的；若Lyapunov指數(shù)為正，表明系統(tǒng)的相體積在某個方向上是不斷膨脹和折疊的，導致吸引子中本來鄰近的軌跡變得越來越不相關，從而使初始狀態(tài)不確定的映射隨時間演化時，其行為變得不可預測，即初值敏感性。此時，映射的運動狀態(tài)是混沌的。Lyapunov 指數(shù)的計算在前文已做過敘述，本節(jié)不做贅述。該映射隨控制參數(shù)變化的Lyapunov指數(shù)譜如圖4 所示。從圖4(a)和圖4(b)可以看出，Hénon 映射和2D-SLM 只有在極小參數(shù)范圍內有正的Lyapunov 指數(shù)；從圖4(c)可以看出，系統(tǒng)在(1,5]參數(shù)范圍內都有正的Lyapunov 指數(shù)，與前面給出的理論分析一致。如果映射的控制參數(shù)發(fā)生微小變化，前2 個映射會出現(xiàn)弱混沌，甚至退化為周期行為，而本文映射仍然保持混沌狀態(tài)。其次，映射在(]1,5 參數(shù)范圍內具有2 個正的Lyapunov 指數(shù)，因此映射在(]1,5 范圍內處于超混沌狀態(tài)，相較于前2 個映射，本文映射展示了穩(wěn)健超混沌行為和更復雜的動力學特性。

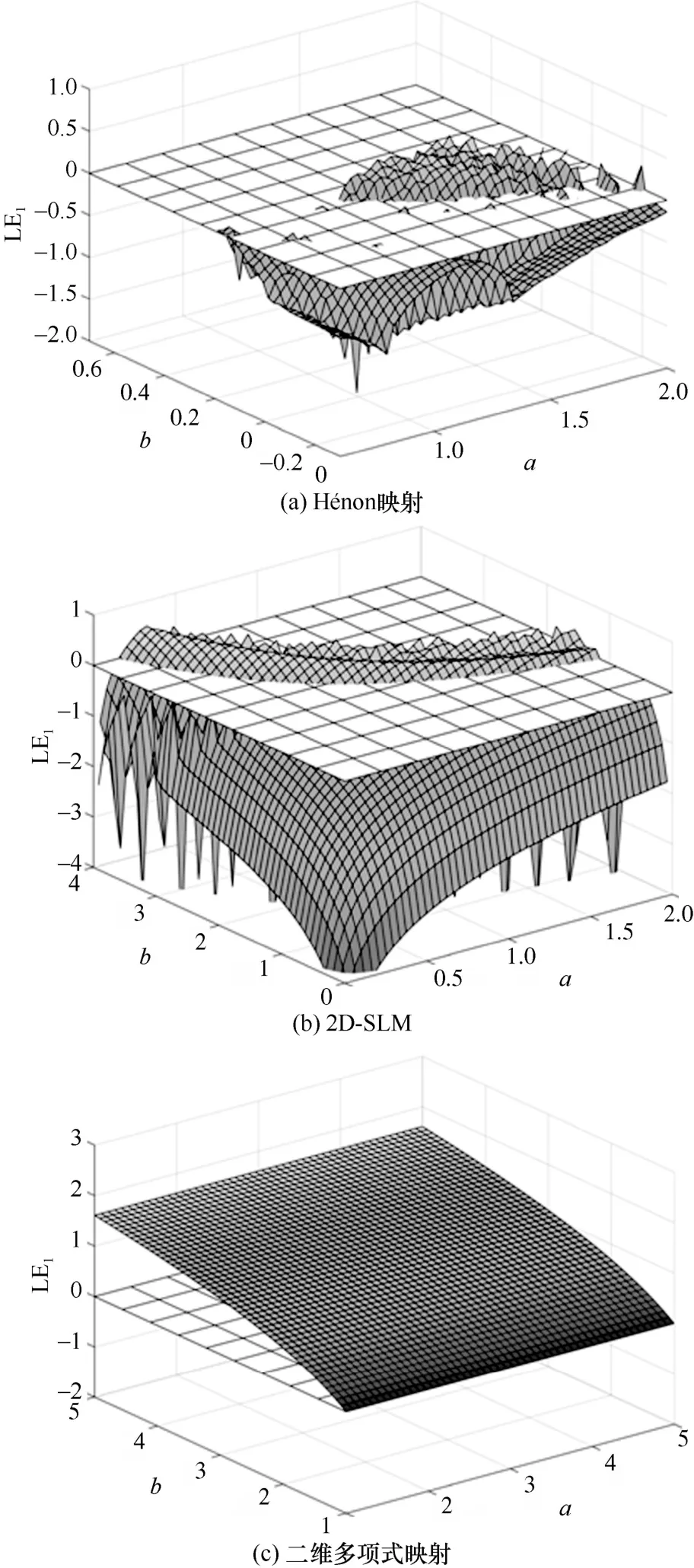
圖4 映射隨2 個參數(shù)變化的Lyapunov 指數(shù)譜

2.4 樣本熵

樣本熵是基于近似熵提出的一種新的生物時間序列復雜度的分析算法[23-24]。該算法取消了近似熵中的自匹配，使其計算更為簡單，計算時間大大縮短，計算的條件概率也更加精確。該算法在計算上采用去除與自身模板比較的方式，擴大了與閾值相比較的偏差值，可以更加準確地估計新數(shù)據出現(xiàn)的概率，降低了近似熵的誤差，是時間序列復雜度量化更加精確的一種算法。近似熵值越接近0，時間序列的自相似性越強，產生新數(shù)據的概率越小，復雜度越低；近似熵值越大，映射的復雜度越高。圖5 展示了不同映射隨參數(shù)變化的近似熵值。從圖5(a)和圖5(b)可以看出，2 個映射在特定范圍內可以取得正的近似熵值，且近似熵值都介于(0 1)，；從圖5(c)可以看出，二維多項式映射的近似熵值在整個區(qū)間都是正的，且近似熵值也大于前2 個映射。這說明了該映射產生的混沌序列具有很高的復雜度，可應用于圖像加密、信息處理和信息傳輸?shù)阮I域。

圖5 映射隨2 個參數(shù)變化的近似熵值

2.5 關聯(lián)維數(shù)

作為分形維數(shù)的一種，關聯(lián)維數(shù)研究的是時間序列所占據空間維數(shù)[25]。時間序列的關聯(lián)維數(shù)的表達式為

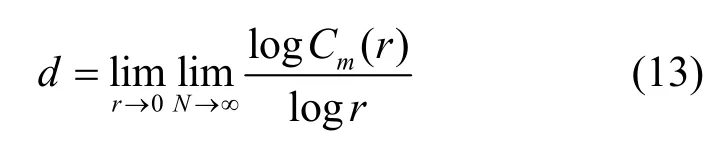
其中，m表示序列的嵌入維數(shù)，r表示嵌入空間球的半徑，表示關聯(lián)函數(shù)，其表達式為

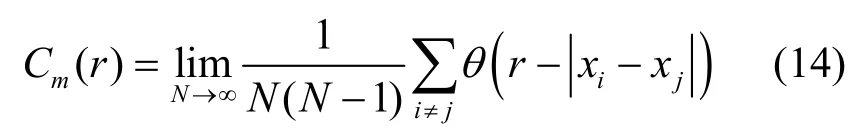
其中，θ(x) 表示階躍函數(shù)表示歐氏空間中Xi與之間的距離，N表示相空間中點的個數(shù)。如果一個非線性映射其輸出序列的關聯(lián)維數(shù)大于0，則表明該非線性映射具有混沌行為。數(shù)值越接近映射的維數(shù)，映射的混沌行為越復雜。表1 展示了4 個混沌映射在給定參數(shù)下的關聯(lián)維數(shù)。相較于其他映射，二維多項式混沌映射的關聯(lián)維數(shù)大于其他3 個系統(tǒng)，表明二維多項式混沌映射產生的時間序列具有更高空間維數(shù)。

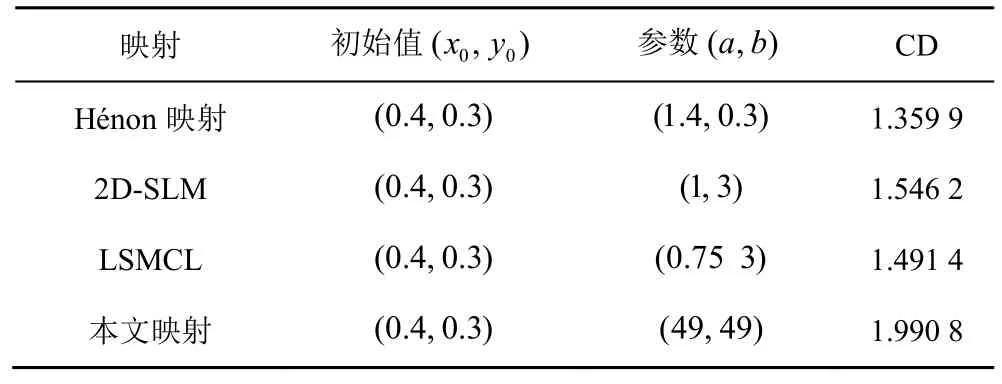
表1 4 個混沌映射在給定參數(shù)的下的關聯(lián)維數(shù)

2.6 隨機性測試

為了證明混沌輸出序列的偽隨機性，本文通過NIST SP 800-22 進行測試。對于NIST 套件中的15項測試，其顯著性水平設置為1%。當P〉0.01 時，該二進制序列就被認為是隨機的，且其置信度為99%，否則被認為是非隨機的。在本文測試中，給定初始值和控制參數(shù)，由于混沌序列的輸出都介于本文采用等式，將十值序列轉化為二值序列。其中是向下取整函數(shù)，di是混沌輸出序列，α是一個很大的數(shù)來影響序列的數(shù)值，β是一個整數(shù)。設，可以得到8 bit 的二進制序列。然后對2 個混沌序列進行NIST 測試，測試結果如表2 所示。在表2 中，所有測試均測試成功，表明所提映射產生的混沌序列具有很強的隨機性。

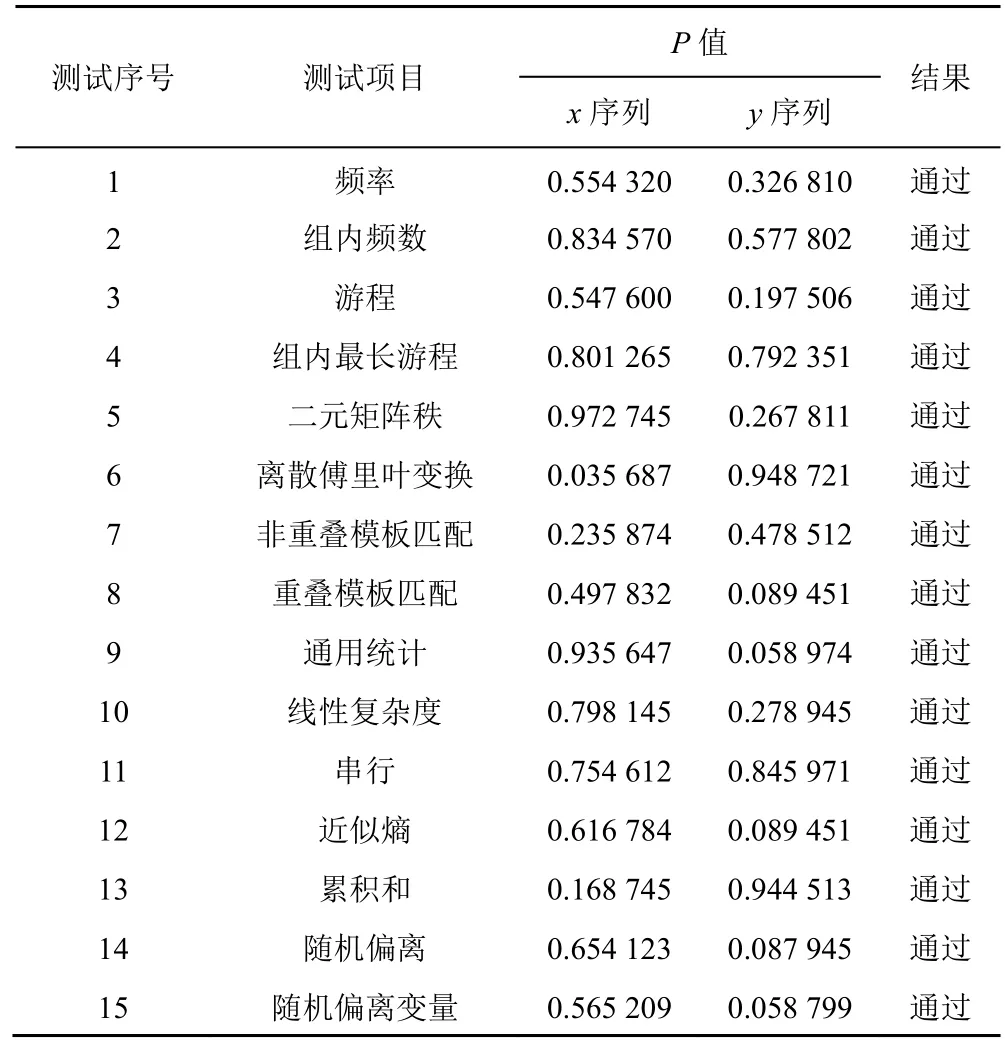
表2 混沌序列的NIST 測試結果

3 混沌映射在信息傳輸中的應用

由于混沌映射的不可預測性以及遍歷性，因此其被廣泛用于網絡傳輸數(shù)據。利用混沌映射產生的序列進行數(shù)據傳輸時，其輸出的分布對傳輸誤碼性能有很大的影響[26-29]。由于本文構造的二維多項式混沌映射的輸出較為均勻地分布在整個取值空間上，因此使該混沌映射在安全通信中可以表現(xiàn)出較高的性能。本節(jié)使用參考調制差分混沌移位鍵控（RM-DCSK,reference-modulated differential chaos shift keying）[30]來演示本文所提混沌映射在信息傳輸中的性能。

3.1 RM-DCSK 通信方案

RM-DCSK 通信方案由發(fā)送端和接收端兩部分組成。發(fā)送端首先利用混沌序列對信息比特位進行編碼，生成傳輸信號，然后將傳輸信號發(fā)送給接收端。接收端對接收信號進行解碼，從而恢復出信息比特位。

1) 發(fā)送端。傳輸信號的結構如圖6 所示，b2k是第2k個信息比特位，Xk是一條長度為M的混沌序列，表達式為為擴頻指數(shù)。RM-DCSK 通信方案的發(fā)送端結構如圖7所示。首先，將系統(tǒng)的第一個時隙設置為參考時隙，混沌信號xi作為信息載波在第一個時隙內傳輸比特信息b2k，而第二個時隙是兩部分之和，前一部分是將上一個時隙傳輸?shù)男畔⒆鳛樾畔⑤d波，然后在第二個時隙內傳輸比特信息b2k1+，而后一部分是本時隙的混沌序列，即xi。則第k幀的傳輸信號si的表達式為

圖6 傳輸信號的結構

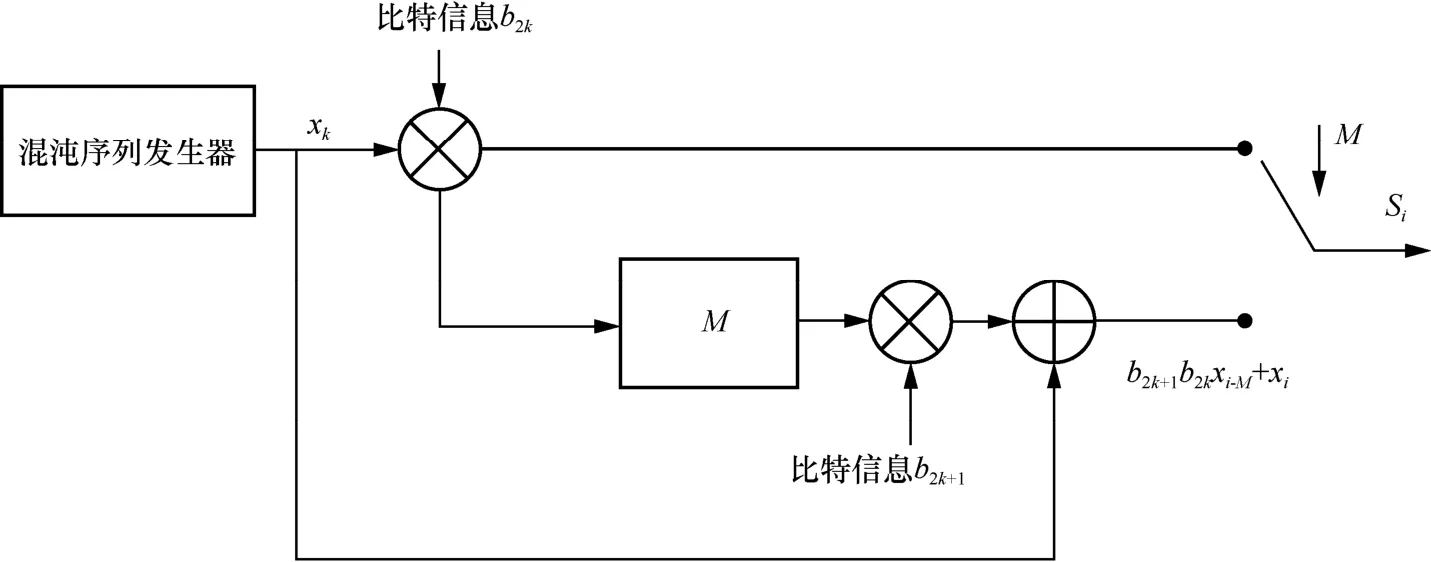
圖7 RM-DCSK 通信方案的發(fā)送端結構

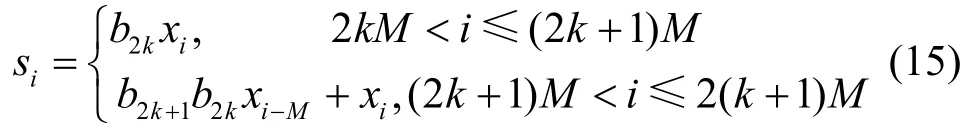
其中，混沌樣點xi滿足

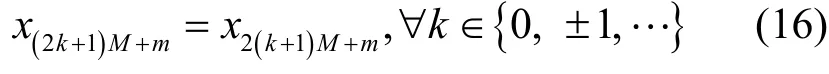
2) 接收端。當接收端從發(fā)送端接收到傳輸信號時，可以利用相關器恢復原始信息比特位。RM-DCSK通信方案在解調時主要利用了混沌延遲特點和非相干技術，接收端結構如圖8 所示。由于信號在不同網絡中傳輸時可能會受到噪聲的干擾，因此接收到的信號與原始信號有所不同。本文主要以加性白高斯噪聲（AWGN，additive white Gaussian noise）信道模型作為主要通信傳輸媒介，信道中的干擾以加性白高斯噪聲ξi為主，且則接收到的信號ri為

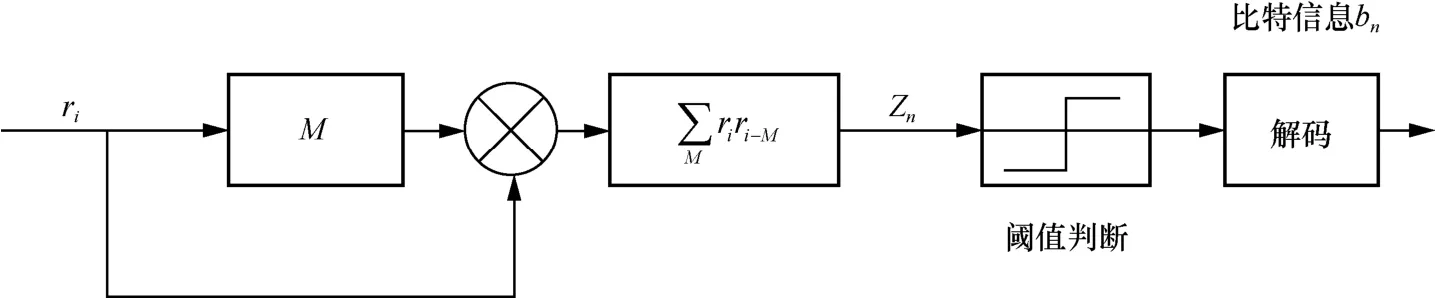
圖8 RM-DCSK 方案的接收端結構

相關器Zn為

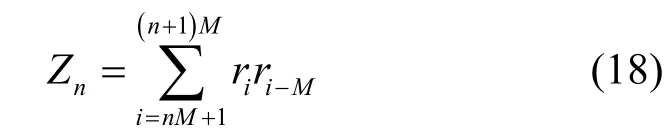
恢復出信息比特位b2k的相關器Z2k為

3.2 仿真實驗

為了證明本文構造的混沌映射在RM-DCSK 中的優(yōu)良特性，本文對比了現(xiàn)有的4 種二維離散混沌映射，如經典的Hénon混沌映射、2D-SLM、2D-LSMCM、文獻[19]混沌映射。在不同的擴頻指數(shù)M及不同等級噪聲的AWGN 信道模型中，本文使用以上混沌序列發(fā)生器進行了RM-DCSK 通信方案的仿真。每次實驗傳輸數(shù)據是一個隨機生成的1×105bit 長度的二進制序列。通過計算接收到的數(shù)據與原始數(shù)據之間的誤碼率（BER,bit error ratio）來驗證其抗噪聲能力。第一組研究針對不同擴頻指數(shù)下的誤碼率。對于每個混沌映射，實驗設置如下。

1) 選取5 種混沌映射中的xn序列對信息比特進行編碼。

2) 設置AWGN 通道的噪聲強度為26 dB，在不同的擴頻指數(shù)下，計算RM-DCSK 通信方案的誤碼率。

3) 在不同初始值下重復步驟1) 和步驟2) 10 次。

4) 計算這10 次實驗誤碼率的平均值。

第二組研究針對不同噪聲等級下的誤碼率。對于每個混沌映射，實驗設置如下。

1) 選取5 種混沌映射中的xn序列對信息比特進行編碼。

2)設置AWGN 通道的擴頻指數(shù)M=80，在不同的噪聲等級下，計算RM-DCSK 通信方案的誤碼率。

3) 在不同初始值下重復步驟1) 和步驟2) 10 次。

4) 計算這10 次實驗誤碼率的平均值。

從圖9 中可以看出，在不同擴頻指數(shù)M下，RM-DCSK 通信采用本文提出的二維多項式混沌映射總能比其他混沌映射獲得更小的誤碼率。從圖10中可以看出，當信噪比較小時，使用不同混沌映射的RM-DCSK 通信方案可以獲得幾乎相同的誤碼率。但隨著信噪比的增加，使用本文提出的二維多項式混沌映射比使用其他混沌映射可獲得更小的誤碼率。這說明二維多項式混沌映射相較于其他混沌映射更適用于信息傳輸。

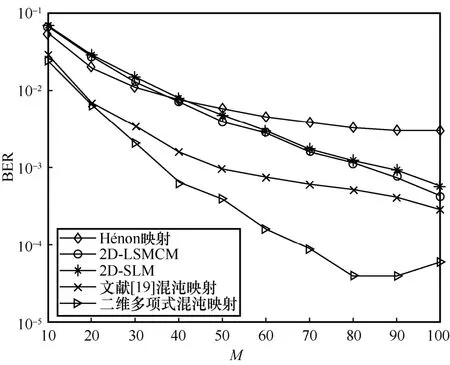
圖9 不同擴頻指數(shù)下RM-DCSK 方案的誤碼率

圖10 不同噪聲等級下RM-DCSK 方案的誤碼率

4 結束語

為了解決離散混沌映射存在著混沌范圍不連續(xù)、輸出分布不完整等缺陷，本文提出了廣義二維多項式混沌映射，并通過理論分析與實驗仿真證實了該映射的有效性，最后將5 種二維混沌映射應用于RM-DCSK 通信方案中。相較于其他混沌映射，本文提出的二維多項式混沌映射可以獲得更小的誤碼率，說明了該映射更適用于信息傳輸。在后續(xù)工作中，本文將基于局域網，利用現(xiàn)場可編程門陣列硬件平臺搭建通信方案模型，RM-DCSK 通信方案可以為加密端和解密端發(fā)送密鑰。