布爾環及其譜的一些性質

郭俊輝

(廣州大學 數學與信息科學學院, 廣東 廣州 510006)

布爾環的出現是由布爾代數作為背景衍生出來的，布爾代數在代數學(代數結構)、邏輯演算、集合論、拓撲空間理論、測度論、概率論和泛函分析等數學分支中均有應用，1967年后, 在數理邏輯的分支之一的公理化集合論以及模型論的理論研究中, 也起著一定的作用。近幾十年來, 布爾代數在自動化技術、電子計算機的邏輯設計等工程技術領域中有重要的應用。布爾代數一詞源于英國數學家Boole,他把邏輯簡化成極為容易和簡單的一種代數。在這種代數中, 適當材料上的“推理”, 成了公式初等運算的事情。例如矛盾律, 即A不能既是B又是非B, 它可表示為x(1-x)=0; 排中律可被說成x+(1-x)=1。“且”對“或”的分配律可以表示為x(u+v)=xu+xv。 這樣, 就使邏輯本身受到數學的支配[1]。為了使自己的研究工作趨于完善, 布爾在此后的漫長時間里, 又付出了不同尋常的努力。1854年, 他發表了《思維規律》這部杰作,布爾代數問世了。后來, Ernst較為系統地給出布爾代數和分配格的定義[2]。在離散數學中, 布爾代數(有時叫布爾格)是有補分配格。首先提出布爾環與布爾格之間的緊密聯系的是Stone。在數學中, 斯通氏布爾代數表示定理聲稱所有布爾代數都同構于集合域。這個定理是深入理解在20世紀上半葉所拓展的布爾代數的基礎，該定理首先由斯通1936年證明, 并以他的姓氏命名。斯通通過對希爾伯特空間上算子譜理論的研究而得出了它。這個定理有多種闡述語言, 例如任意一個布爾代數一定同構于某個集上的一個集合域, 又或者說任意一個布爾代數也一定同構于某個拓撲空間的閉開代數等, 也可以用拓撲學和范疇論的語言來重述如下: 斯通表示定理斷言在布爾代數范疇和斯通氏空間, 也就是完全不連通緊致Hausdorff拓撲空間(也叫做布爾空間)范疇之間的對偶。在本文中,作者試圖要將斯通定理敘述為更為簡單淺顯的一個版本, 即: 任意一個布爾格都與某個緊致的Hausdorff空間中的全體既開又閉的子集合所組成的格同構。在本文的第一部分通過對這個定理的推理,發現了布爾環及其素譜空間的特殊性, 它有著其他一般交換環及對應素譜不一定有的性質。本文在第二部分正是利用了布爾環的特殊性質推廣了一個在一般交換環上成立的命題: 有限個素理若想可以覆蓋一個理想, 則必有其中一個素理想覆蓋住該理想。在布爾環中, 借助譜的知識, 該命題中的條件“有限個”在某種條件下可以去掉。在文章的末尾, 則單獨探究布爾環譜空間的拓撲性質, 除了發現這種空間是“散碎的”、完全不連通的, 還發現當將譜空間的經典拓撲(Zariski拓撲)劃分得更細, 劃成可構造拓撲時, 兩種情況實際上是一回事, 即根本沒有變得“更細”。

1 斯通定理

斯通表示定理在數學史上影響深遠, 正如上文所說, 斯通定理在不同的場合下表達出來的語言也是不一樣的, 又例如這樣的表達: 任一布爾代數同構于其全體極大濾子構成的緊致零維 Hausdorff空間中的開閉集代數。受斯通定理的思維火花影響, 不少學者繼而不斷揭示偏序集與拓撲空間之間的關系[3-5]。隨著研究的加深, 近年來多值邏輯也有較快的發展[6-7], 而一些具有蘊含性質的格, 例如R0-代數、BL-代數、MTL-代數等也相繼被提出。自然地, 一些斯通定理的推廣工作也相繼進行著, 如在R0-代數上推廣了布爾代數的斯通定理[8-9]。也有一些學者, 例如劉應明等[5]對某類完全分配格給出了斯通定理的格值形式, 用范疇的語言說, 即分配格范疇對偶同構于凝聚L-locale范疇, (前提是)若格L是一個frame且0∈L是素元或1∈L是余素元。更進一步, 假若L還是完全分配的, 則分配格范疇對偶同構于凝聚滿層L-拓撲空間范疇。由以上敘述可感知斯通定理至今還不斷煥發著它的活力, 歸根結底是因為斯通表示定理揭示了格論與拓撲空間理論之間的深刻聯系, 而王國俊[10]更是有創意地將斯通表示定理與廣義空間理論以及拓撲分子格理論這些新學科聯系起來研究。同樣讓人印象深刻的是郭鐵信等[11]于2011年在復完備隨機內積模上的隨機酉算子群上面建立了斯通表示定理。在國外的一些研究中, 有不少學者把注意力投向了布爾超代數, 先是Procesi等在文獻[12]中證明了布爾超代數上的斯通表示定理, 后來Procesi在文獻[13]中用拓撲的角度看待問題, 并用拓撲語言闡述了布爾超代數上的斯通表示定理。

本文中提到的布爾環是所有元素都滿足x2=x的含幺交換環。以下首先介紹有關格的概念。格是一種特殊的偏序集, 經過特殊化以后得到分配格, 再特殊化以后可以得到布爾代數, 是序結構的主體部分。在許多數學對象中, 所考慮的元素之間具有某種順序。例如一組實數間的大小順序, 一組命題間的蘊涵順序等。這種順序一般不是全序, 即不是任意2個元素之間都能排列順序, 而是在部分元素之間的一種順序, 稱為偏序。偏序集和格就是研究順序的性質及作用而產生的概念和理論。格是其非空有限子集都有一個上確界和一個下確界的偏序集合。在19世紀的后幾十年, 德國數學家戴德金和施履德分別從數論和邏輯代數兩個方向得出格的概念。但是其他數學家并未認識到它的重要性。直至20世紀30年代, 在美國數學家伯克霍夫和挪威數學家奧爾的共同努力下, 格論才煥發生機, 發展成為一門獨立的數學學科, 在抽象代數、射影幾何、點集論、拓撲學、泛函分析、邏輯和概率論等諸多領域產生廣泛應用。例如在代數學中對于一個群與其子群格之間關系的研究, 在數理邏輯中關于不可解度的研究。在圖論中關于圖分解的研究也大量用到格論。在密碼學領域, 關于公鑰密碼分析學的應用研究也常用到格理論及格基約減算法。

首先需要談及格的定義, 它有2種定義, 一種是代數定義, 另一種是偏序定義, 2種定義相互等價且在談論格的時候永遠不要將2種定義割裂來看。

定義1[14](格的代數定義) 設L為一個集合, 在L上定義2種在L中封閉的運算∨和∧, 使得對任意a,b∈L滿足以下性質:

(1) 交換律a∨b=b∨a,a∧b=b∧a;

(2) 結合律a∨(b∨c)=(a∨b)∨c,a∧(b∧c)=(a∧b)∧c;

(3) 冪等律a∨a=a,a∧a=a;

(4) 吸收律a∨(a∧b)=a,a∧(a∨b)=a。

則稱(L,∨,∧)是一個格。

定義2[14](格的偏序定義) 設L是一個偏序集, 且使得任意2個元素構成的子集{a,b}一定有上確界(最小上界)和下確界(最大上界), 則稱(L,≤)是一個格。

以上2種定義是相互等價的, 有了定義1, 可定義偏序關系為a≤b當且僅當a∧b=a, 或者等價地說a∨b=b(容易驗證這樣定義的關系確實為偏序關系), 則有

inf{a,b}=a∧b,sup{a,b}=a∨b。

反之, 由定義2出發, 可分別定義2種運算為

a∨b=sup{a,b}和a∧b=inf{a,b}。

容易驗證這樣定義的運算∨和∧滿足以上定義1中公理化要求的4個律[14]。自然地, 關于格同構也有2種相對應的等價敘述[14]: 格L1與L2同構是指能夠建立L1到L2的一一映射φ使得映射φ可以保持2個運算∨和∧, 或者等價地說,φ和φ-1都是保序的, 其中，φ-1是保序的這一條件是不可省略的。

布爾格是一種特殊的格, 就好比布爾環是一種特殊的環。布爾格的定義則要在格的定義上再加多幾個公理化要求。

定義3[15]設(L,∨,∧,≤)是一個格, 如果再有以下的性質被滿足:

(1)L中有最大元和最小元(分別記作1和0);

(2)2個運算“∨”和“∧”都對另一個滿足分配律, 即

(a∨b)∧c=(a∧c)∨(b∧c),

(a∧b)∨c=(a∨c)∧(b∨c);

(3)任意一個元a∈L, 存在唯一的補元a′∈L使得

a∨a′=1,a∧a′=0，

則稱這種格是布爾格。

下面將指出布爾環和布爾格其實本質上是一回事, 兩者互相誘導, 一一對應, 從而為后面闡明斯通定理做出鋪墊準備。

引理1[15-16]布爾環和布爾格相互誘導, 一一對應。

現在介紹一些布爾環的性質, 以及交換環的素譜概念和布爾環的譜上性質。

引理2 交換環中若任意一個元素x∈A都有某個n∈且n>1, 使得xn=x, (n依賴于x), 則A中所有素理想都是極大理想。

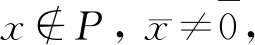
x(1-xn-1)=0,

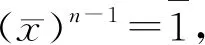
若n>2, 則

找到了逆元, 證畢。

命題1 在布爾環中有

(1)對一切x∈A,有2x=0;

(2)任意的素理想P都極大,且A/P是只有0與1的域;

(3)有限生成的理想是主理想。

證明

(1)這是較顯然的;

(2)由引理2, 即可得；

(3)只需證明由2個元素生成的理想是主理想即可。現證明以下斷言即可, 即

(x,y)=(x+y+xy)。

(x+y+xy)?(x,y)是顯然的; 反過來, 由(1)的結論, 有

x(x+y+xy)=x,y(x+y+xy)=y，

故(x,y)?(x+y+xy), 斷言成立。同理對3個元素的情況也有

(x,y,z)=(x+y+z+xy+xz+yz+xyz),

以此類推, 證畢。

以下簡單提及交換環的素譜概念[15]。這是一個在代數幾何中很基本的概念, 有的時候談及環的局部化都會必不可少地談及素譜。環的素譜和譜空間理論起源于仿射代數簇(又稱代數流形)的研究。現已廣泛應用于許多數學分支中, 如代數幾何、層論、C*-代數、拓撲學、環論、模論、格論和群論等。幾何性質和代數性質之間會相互反饋信息。每一個幾何性質都會返回一個代數性質, 例如層(Sheaf), 那么反過來代數性質也能返回一個幾何性質, 例如素譜, 合在一起就成了概型(Schemes)。素譜的概念在交換代數以及代數幾何中扮演了一個很基礎的角色, 就好比小學課本中的加減運算。素譜的可研究價值極大, 例如從范疇論的角度去看, 素譜還具備函子性: 素譜可以視作反變函子。更多性質細節可參考文獻[15]。設A是一個交換環,X是它所有素理想的集合, 設E是A中的子集,α是E所生成的理想, 記

V(E)={P∈X|P?E},

則有以下性質:

(2)V(0)=X,V(1)=?；

(3)設(Ei)i∈I是A中的一個子集簇, 那么V(∪i∈IEi)=∩i∈IV(Ei)；

(4)設α,β是A中任意2個理想, 則V(α)∪V(β)=V(α∩β)=V(αβ)。

從以上性質可以看出形如V(E)的全體所構成的集族滿足閉集的拓撲公理, 于是X可以構成一個拓撲空間, 定義X中的閉集: 子集F為閉集當且僅當F可表成上述V(E)的形式。該拓撲空間(X,τ)叫環A的素譜(記為Spec(A)), 這個拓撲τ稱為Zariski拓撲。

注記1 Zariski拓撲并不是人們在X上研究的唯一拓撲, 只是研究的最多的拓撲, 如無特別聲明, 都是認為素譜上的拓撲是Zariski拓撲。另外比較多見的拓撲是可構造拓撲(記為τc), 在文章后面會提及關于布爾環在可構造拓撲下的素譜的相關性質特點。任意交換環在Zariski拓撲或者可構造拓撲下的素譜空間都是緊致的[15]。

注記2 對任意交換環A中的任意元素f, 定義

Xf=X[V((f))]={P∈X|f?P},

則Xf顯然是(X,τ)中的開集, 并且全體形如Xf的集族能構成(X,τ)的一組拓撲基[14]。且有以下性質:

(1)Xf∩Xg=Xfg；

(2)Xf=??f是冪零元；

(3)Xf=X?f是可逆元。

更詳細的性質可參考文獻[14]。

命題2[15-16]設A是布爾環, (X,τ)是帶有Zariski拓撲的A的素譜空間, 則

(1)每一個Xf在(X,τ)中既開又閉；

(2)對有限個f1,…,fn∈A, 存在f0∈A, 使得Xf1∪…∪Xfn=Xf0；

(3)形如Xf的集合是(X,τ)中僅有的既開又閉的子集；

(4)(X,τ) 是緊致的Hausdorff空間。

證明(1)～(4)在文獻[15-16]中都有涉及。這里簡單提及(2), 要解決有限個的情形只要解決2個的情形即可, 結合命題1中的(3), 有

Xf∪Xg=[V((f))∩V((g))]c=

[V({f,g})]c=

[V((f+g+fg))]c=Xf+g+fg。

在本文的下一個部分由(4)會推出深刻的結論。

結合以上的鋪墊得到最后的斯通定理:

定理1[3,15](斯通定理) 任意一個布爾格都與某個緊致的Hausdorff空間中的全體既開又閉的子集合所組成的格同構。

證明給出任意的一個布爾格(L,∨,∧,≤), 根據引理1, 設A是與之對應的布爾環, (X,τ)是環的譜, ∑={Xf|f∈A}, 則∑是緊致的Hausdorff空間(X,τ)中全體既開又閉的子集集合, 定義偏序關系為集合的包含關系, 即

Xf≤Xg?Xf?Xg,

這種情況下對應的運算“∨”和“∧”實際上就是集合的并和交，則容易驗證(∑,∨,∧,≤)構成一個格。下面驗證格同構(L,∨,∧,≤)?(∑,∨,∧,≤)，定義映射：

φ:L→∑為φ(f)=Xf,

則根據引理1以及命題2可得:

φ(f∨g)=φ(f+g+fg)=Xf+g+fg=

Xf∨Xg=φ(f)∨φ(g)。

根據注記2中的性質(Xf∩Xg=Xfg), 有

φ(f∧g)=φ(fg)=Xfg=Xf∧Xg=φ(f)∧φ(g)。

通過驗證,φ確實保持運算“∨”和“∧”, 因而是格同構, 從而完成了證明。

2 布爾環的素譜的一些性質

以上通過推理出斯通定理的一個簡單形式，發現了布爾環的獨特性, 并且這種獨特性會轉嫁到它的素譜中, 使得它的素譜也是一個很特別的拓撲空間。在這個部分,將特別研究布爾環的素譜的一些性質。

布爾環所具備的特殊性, 首先可以用來拓展一個在普通的交換環上很重要且經常使用但是又難以拓展的性質: 若存在有限個素理想可以覆蓋一個普通的理想, 則必有其中一個素理想覆蓋住該理想。為了闡明這項工作, 先做一些鋪墊準備, 介紹一些相關知識。

命題3 任意的交換環的素譜(X,τ)中,Xg是緊致的子集(對任意的g∈A)。

證明只需證明假若一簇拓撲基中的成員{Xfi}i∈I能夠覆蓋住Xg, 則有有限的子覆蓋即可。設Xg?∪i∈IXfi, 即有蘊含關系:P為A中的素理想,g?P??f0使得f0?P,

等價于

fi∈P,?i?g∈P，

則有等式:

V({fi│i∈I})=V({g,fi|i∈I})。

于是有

得

這就存在有限個fi1,…fik以及某n∈使得

gn=c1fi1+…+cnfik,

則素理想P如果同時包含fi1,…fik, 則會包含gn, 從而包含g, 因而有

證畢。

定義4[17]拓撲空間中的子集族稱為有核的, 如果中任意有限個成員之交非空。

命題4[17]拓撲空間(X,τ)緊致當且僅當X的任意有核閉集族之交∩A∈A≠?。

借助布爾環的特殊性,可對上面的問題做出其中一種回答, 具體的表述如下:

命題5 在布爾環A中, 設X是它的素譜, 設理想α?∪P∈XfP, 則必存在某P0∈Xf使得α?P0。

證明集族{V((a))∩Xf|a∈α}是緊致的子空間Xf上的閉集族, 并且是有核的, 事實上,

[V((a1))∩Xf]∩…∩[V((an))∩Xf]=

V((a1,…,an))∩Xf=V((a0))∩Xf,

其中，(a1,…,an)=(a0)是由命題1(3)得來, 且a0∈α, 由α?∪P∈XfP可知會存在某個P′∈Xf使得a0∈P′, 則

P′∈V((a0))∩Xf,

即集族{V((a))∩Xf|a∈α}是有核閉集族, 根據命題4, 集族{V((a))∩Xf|a∈α}全員之交非空, 則會存在一個P0∈Xf使得

P0a, ?a∈α,

即

α?P0,

證畢。

注記3 以上命題條件中的Xf當然也可以換成某個V(E), 因為V(E)是緊致空間中的閉集, 從而也是緊致的[17], 然后用同樣的方法去證明。

關于布爾環的素譜空間有一個很特別的拓撲性質, 就是完全不連通, 即任意一個至少含2點的子集都是不連通的, 也就是說連通的子集只能是單點集。由于布爾代數的影響很大且性質獨特, 故和布爾代數相掛鉤的研究對象也變得“特別”了, 例如現在討論的布爾環的素譜空間。所以, 完全不連通的緊致的Hausdorff空間就被人們特別地稱為“布爾空間”[3,14-15]。根據文獻[18]的引理3.1，至少可以知道非平凡含幺布爾環的素譜空間一定是不連通的，但是僅僅得出這個結論還遠遠不夠，所以有下面的命題6：

命題6 布爾環的素譜空間是布爾空間。

證明根據命題2(4), 只需證明(X,τ)中任意一個至少含2點的子集F都是不連通的即可。設

P1,P2∈F?X且P1≠P2,

則存在某個Xf使得P1∈Xf且P2?Xf, 無疑Xf是開集, 但是它也是閉集, 根據命題3,Xf是緊致的子集, 在緊致的Hausdorff空間中緊致子集等價于閉集[17], 所以Xf既開又閉。故Xf∩F是F中既開又閉的真子集(含P1卻不含P2), 所以F不連通。

注記1中提到的可構造拓撲τc, 一方面提及這種拓撲的一個原因是可構造拓撲本身也是交換環的素譜上的重要研究對象, 另一方面, 針對本文著重研究的布爾環, 它的素譜上的可構造拓撲有著一個有趣的事實: 布爾環的素譜帶上Zariski拓撲和帶上可構造拓撲其實是一回事。

先介紹什么是可構造拓撲。

定義5[15]對任意的交換環A, 記X為A的全體素理想的集合, 記

τc={U?X│存在交換環B以及環同態f:A→B,使得XU=f*(Spec(B))},

其中,f*:Spec(B)→Spec(A)定義為: 對任意的q∈Spec(B), 有

f*(q)=f-1(q)∈Spec(A),

τc能夠構成一個拓撲從而使(X,τc)成為一個拓撲空間, 稱τc為X上的可構造拓撲。

注記4 對以上τc的拓撲公理的驗證, 只需驗證閉集的拓撲公理即可[15]:

(1)設有一族交換環Bi以及相配的環同態fi:A→Bi,i∈I, 指標集I可以是無窮集, 則有

記指標集

∑={J|J?I,是I中的有限集},

定義∑中的序關系:

J≤K?J?K,

則∑是一個正向集 (即特殊的偏序集, 滿足對任意的2個指標i,j都會存在某個指標k使得i≤k以及j≤k), 因為對任意的J,K∈∑有

J∪K∈∑,J?J∪K,K?J∪K,

對任意的指標J≤K, 有典范的A代數同態

μJK:BJ→BK,

則(BJ,μJK)構成一個正向系統[15]。最后定義無窮個A代數Bi的張量積為該正向系統的正向極限, 即

(i)設(Bi,gij)是一個環的正向系統,B是正向極限, 對每個i都有環同態fi:A→Bi, 且對任意的i≤j都有gij°fi=fj(即(Bi,gij)構成A代數的正向系統)。fi自然誘導出f:A→B, 則有結論

(ii)設有環同態f:A→B以及g:A→C, 定義同態h:A→B?AC為

h(a)=f(a)?1,

則有結論:

h*(Spec(B?AC))=f*(Spec(B))∩g*(Spec(C))。

至此, 結合(i)與(ii)的結果就自然得到

(2)設有環同態:f1:A→B1以及f2:A→B2, 定義環同態:f:A→B1×B2為

f(a)=(f1(a),f2(a)),

則有

f*(Spec(B1×B2))=f1(Spec(B1))∪f2(Spec(B2))。

(3)對于零同態:f:A→0, 有f*(Spec(0))=?。

(4)對于恒同映射id:A→A, 有(id)*(Spec(A))=X。

命題7 可構造拓撲比Zariski拓撲更大(或者說更細), 即τ?τc。

證明只需證明Zariski拓撲中的閉集一定是可構造拓撲中的閉集即可。任取Zariski拓撲中的一個閉集V(α), 其中α是任意一個A中的理想。有典范同態

π:A→A/α,

則有V(α)=π*(Spec(A/α)), 證畢。

命題8 可構造拓撲是使得交換環的素譜中Xf既開又閉的最小拓撲(任意的f∈A)。

證明(1) 首先證明Xf在可構造拓撲中既開又閉, 是開的已經顯然了。記Af是A的分式環, 即其中的乘法封閉子集是f的所有次冪(含1=f0)所構成的集合, 則有典范同態

φ:A→Af,

則Xf=φ*(Spec(Af))。從而Xf也是閉集。

(2)設τΩ是定義在X上的使得任意Xf既開又閉的拓撲, 需要證明

τc?τΩ,

即需要證明對任意的ψ:A→B,ψ*(Spec(B))是(X,τΩ)中的閉集。

設

P1?ψ*(Spec(B)),

則P1因為有P是B中的一個素理想的局限當且僅當P=Pec這一等價條件[15]。取f?P1且則設

其中，gi∈P1,bi∈B。則

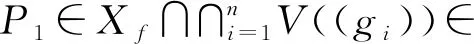
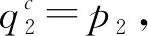
因此

這與P2∈Xf相矛盾。綜上可得ψ*(Spec(B))是(X,τΩ)中的閉集。

有了以上的鋪墊工作, 現在可以說在布爾環上的Zariski拓撲和可構造拓撲是一回事。由命題2知道布爾環上的Zariski拓撲是使得每一個Xf既開又閉的拓撲, 所以由命題8可知τc?τ, 又由命題7得τ?τc, 綜上可得這2種拓撲實際上是一回事。