無窮級數斂散性的判別方法探討
顧 榮
江蘇財經職業技術學院 江蘇淮安 223003

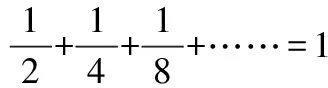


是不是無窮多項的和一定存在呢?我們再來看一個例子:
1+2+4+8+……
基本的數學知識告訴我們,正數相加得到的結果肯定仍然是正數。這里我們假設1+2+4+8+……=,等式左側我們可以變形為:
1+2×(1+2+4+……)=1+2
所以,我們可以得到:=1+2,由此得出=-1,即1+2+4+8+……=-1。顯然,這個結果是錯誤的,原因就在于我們的假設出了問題。有限項的和是一個確定的數,那么無窮多項的和也一定是確定的數嗎?有限項和的運算方法對無窮多項還適用嗎?從有限到無限僅僅是簡單的數的累加嗎?這些其實就是無窮級數的斂散性問題。
一、無窮級數斂散性的判別法及其局限性
(一)利用部分和數列的極限情況判別
在前面“一尺之錘”的例子中,要計算一直取下去,所取得的木棒長度,我們可以先計算取了天后,所得的木棒長度,則:
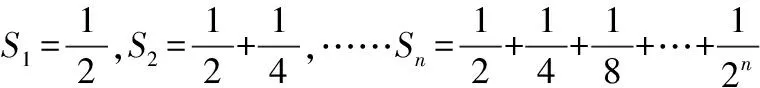
顯然以,,……為項,構成了一個數列{},該數列稱之為部分和數列。

當→∞時,有→1,這也就意味著當木棒一直取下去,所取得的木棒總長度無限接近于1。即:
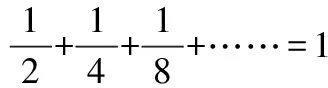


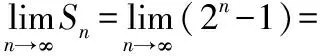
在運用基本判別法討論無窮級數斂散性時,要求出前項和,我們經常會用到一種方法“拆項相消”。


但是這種方法只適用于部分和是容易求的,或者一般項是容易拆項的,且求和后可以“相消”的級數,但是對于一般項較為復雜的級數,該方法就難以判別斂散性。
(二)利用級數的性質進行判別


還有一些特殊級數我們可以通過將原級數加括號,如果加括號后的級數發散,則可以得到原級數也發散。
例如:

將級數兩項兩項加括號后,可得:


由調和級數斂散性,可得加括號后的級數發散,因此原級數也發散。但是如果加括號后的級數收斂,則無法得到原級數一定收斂。因此,對于一些簡單的級數,我們可以利用性質快速判別斂散性。
(三)利用級數收斂的必要條件判別



由級數收斂的必要條件告訴我們,判別級數的斂散性,首先要分析該級數的一般項的極限是否為0,如果一般項的極限不為0,則直接可以得到級數發散。


(四)利用比較、比值、根植審斂法判別
比較、比值、根植判別法使用時首先需要清楚的是,它們只適用于正項級數的斂散性判別,因此在判別級數斂散性之前要先辨析該級數是不是正項級數。

比值、根植判別法在使用時,一般用于中出現了、、!等情況,但是當極限值為1的時候,這兩種方法失效。




(五)利用萊布尼茲審斂法判別
萊布尼茲審斂法只適用于交錯級數的判別,并且只能判別收斂的交錯級數。該審斂法在使用時需要討論一般項的單調性,所以有時需要通過函數的單調性來討論。
(六)利用絕對收斂來判別






二、無窮級數斂散性的判別流程及舉例
級數斂散性的判別方法有很多,但是有些判別方法又具有一定的局限性,只能判別某一類級數的斂散性。這就導致很多學生在面對具體級數斂散性的討論時,徒有很多方法,卻往往不知所措。因此,在掌握了各種判別方法的基礎上,要能夠靈活運用各種判別方法,取長補短,準確地分析具體問題的解決方法,就需要理清楚級數斂散性判別的流程。

斂散性判別流程圖
首先看級數的一般項的極限是否為0,如果不為0,則可以直接判定該級數發散;若極限等于0,則需觀察級數是否為正項級數;若是,則利用比值或根植判別法判別,當比值、根植判別法失效時需要使用比較判別法或者利用部分和數列極限情況來討論斂散性。如果不是正項級數,則需根據項的排列規律分析級數是否為交錯級數。若是,則使用萊布尼茲判別法判斷級數是否滿足條件,如果滿足條件,則級數收斂,否則,需要判斷絕對收斂性,即轉化為正項級數討論。如果級數既不是正項級數也不是交錯級數,則也需要通過絕對收斂性判斷。
下面通過幾個例子說明如何根據上圖中的流程來判別級數的斂散性。



分析:該級數中含有參數,且一般項中含有,所以需要對參數范圍進行分類討論:



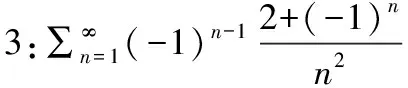






由以上幾個例子可以看出,對于某一無窮級數斂散性的討論,可能需要用到多種判別方法,這就需要我們能夠靈活地掌握判別方法以及基本流程。但是無論如何,題目都是“萬變不離其宗”,復雜的題目可以讓我們在解題過程中多一份感受,也更深刻地認識它的本質。

