基于粒子群優(yōu)化的波束空間廣義旁瓣相消算法

李浩洋，向建軍，彭 芳，王 帥，李志軍

（空軍工程大學航空工程學院，陜西 西安 710038）

0 引 言

自適應陣列天線能夠選擇一組振幅和相位權重，并與輸入信號相結合，產(chǎn)生一個人工控制的波束圖，優(yōu)化所接收到的期望信號。這種形式的陣列處理方法提高了信號處理的抗干擾性能。自適應波束形成技術正廣泛應用于軍事雷達、通信、導航等眾多領域。

在實際應用中，為了獲得更好的分辨率和抗干擾能力，通常使用大規(guī)模陣列天線，這就會導致算法運算量增加，成為實現(xiàn)自適應波束形成算法的瓶頸。算法的運算量通常來自于自適應自由度，為了降低算法的運算量，通常采用部分自適應自由度的方法。降秩自適應波束形成是一種常用的采用部分自適應自由度的方法，主要有特征分解類算法，包括主分量法、交叉譜估計法。在實際應用中，由于特征分解類算法復雜度較高，往往在實際工程中難以應用。針對此類問題，文獻［5］提出了波束空間預處理的方法，通過對波束進行預處理，降低了運算空間的維度，有效減少了運算量并抑制干擾。進行波束空間預處理的關鍵在于確定轉(zhuǎn)換矩陣，通常轉(zhuǎn)換矩陣采用無數(shù)據(jù)約束的方法確定，但當旁瓣出現(xiàn)強干擾時，這種方法難以有效抑制。文獻［7］和文獻［8］提出了一種高效自適應波束域轉(zhuǎn)化方法，能夠根據(jù)接收數(shù)據(jù)及時更新轉(zhuǎn)換矩陣，有效抑制干擾，但由于采用特征分解的方法會導致算法復雜度增加。本文針對上述問題，提出了一種簡便的自適應波束域轉(zhuǎn)化方法，不需要特征分解來求解轉(zhuǎn)換矩陣，使算法更易實現(xiàn)。采用這種方法處理廣義旁瓣相消（generalized sidelobe canceller，GSC）算法可以得到波束空間GSC（beam space GSC，BS-GSC）算法。

由于自適應波束形成需要求解復雜的非線性問題，利用傳統(tǒng)的數(shù)學解析方法和數(shù)值優(yōu)化往往難以取得期望效果。粒子群優(yōu)化（particle swarm optimization，PSO）算法是一種具有全局搜索能力的非線性約束優(yōu)化算法，具有很強的穩(wěn)健性，適用于解決非線性優(yōu)化問題。文獻［10］提出的改進PSO算法應用在波束形成中，起到了降低旁瓣和加深零陷的效果，但是存在收斂早熟、易于陷入局部最優(yōu)、搜索范圍小等問題。文獻［11］針對PSO算法易于陷入早熟等問題提出了壓縮因子的方法，使PSO算法的收斂效率有效提升。PSO算法在陣元空間起到了較好波束形成的效果，但目前還沒應用到波束空間中。本文提出了一種基于PSO優(yōu)化的BS-GSC算法，該算法在保證波束形成效果的基礎上顯著降低算法的運算量，并通過粒子群尋優(yōu)手段有效降低波束形成旁瓣，提高了算法在低快拍、強干擾條件下的波束形成能力。

1 信號模型及GSC算法基本原理

在均勻線陣平面內(nèi)，假設有個不相關窄帶信號從遠場入射到個陣元中，陣元間距為，信號入射角為θ（＝1，2，…，），在遠場空間有一個期望信號（）（其來波方向為）和個干擾信號S（）（＝2，3，…，＋1）（其來波方向為θ），每個陣元中的加性高斯白噪聲為（）。本文考慮信源與陣列平面共面的情形。陣列接收數(shù)據(jù)矩陣可以表示為

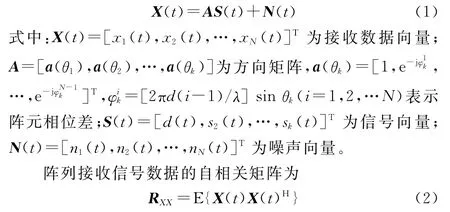
在實際情況中，由于接收的信號數(shù)據(jù)是有限的，接收數(shù)據(jù)是通過有限快拍數(shù)得到的，在有限快拍數(shù)下的自相關矩陣為

本文采用GSC算法對上述問題分析，其結構如圖1所示。圖1中，（）為輸入信號，（）為輸出信號。

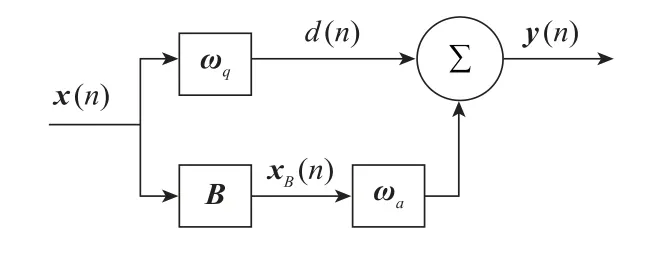
圖1 傳統(tǒng)GSC結構框圖Fig.1 Structure block diagram of traditional GSC

GSC結構將信號分為兩個支路，在上支路中ω為固定波束形成權矢量：

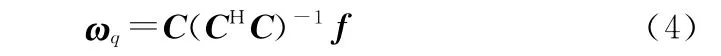
式中：＝［（），（），…，（θ）］為約束矩陣；為相對應的約束響應矢量。

在下支路中，為達到阻塞期望信號的目的，通常在自適應權矢量ω前添加阻塞矩陣，阻塞矩陣需要滿足＝0。通過自適應權矢量ω讓x （）逼近期望信號（），可以依據(jù)最小均方誤差原則進行維納濾波：

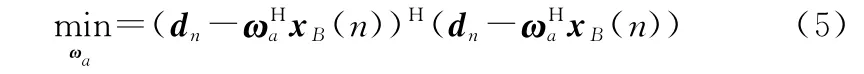
求得自適應權矢量ω為

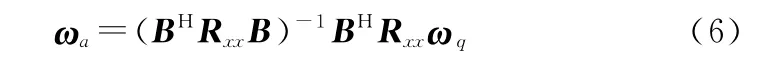
最終得到的GSC的權矢量可以寫為

2 基于粒子群的BS-GSC算法原理與流程

2.1 BS-GSC算法

針對傳統(tǒng)GSC算法在信號處理過程中陣元數(shù)量多，導致算法的運算量較大、運算時間長、復雜度高的問題，通常采用變換域的方法對陣列接收數(shù)據(jù)進行預處理，通過轉(zhuǎn)換矩陣將信號處理過程由原本的陣元空間轉(zhuǎn)換到空間相對較小的波束空間，從而減小了算法的運算量并提高了算法的穩(wěn)健性。本文選取了一種簡便的自適應波束空間變換方法，該方法可以根據(jù)接收數(shù)據(jù)自適應調(diào)整變換矩陣，有效地提高了運算效率。

首先選擇（＜）個正交波束，根據(jù)陣元導向矢量構建×的無數(shù)據(jù)約束轉(zhuǎn)換矩陣。轉(zhuǎn)化矩陣為

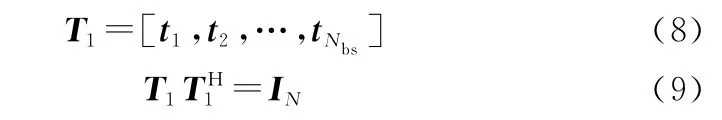
式中：I 為維單位矩 陣。

可以看作由個正交向量t （＝1，2，…，）所張成的子空間。t 根據(jù)正交原理可以表示為

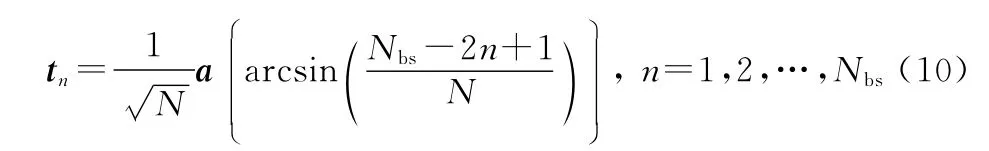
由以上公式可以推出：

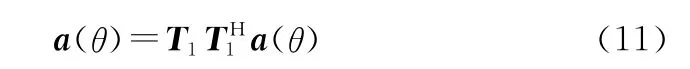
在保證期望角度范圍內(nèi)任意方向的響應均無失真的條件下，自適應調(diào)整轉(zhuǎn)換矩陣，使輸出總功率最小。本文采用最小輸出功率原則，具體準則可以表述為

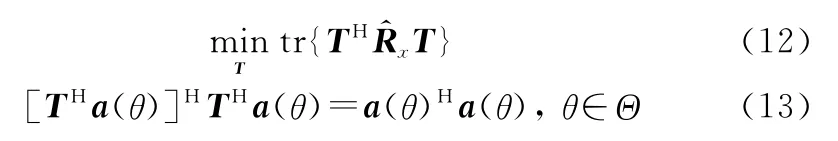
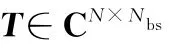
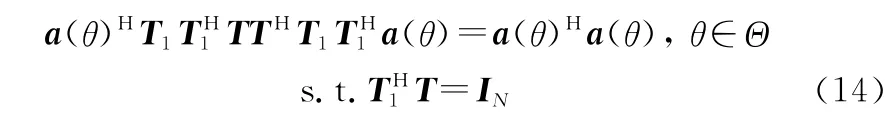
因此，最小輸出功率準則可以轉(zhuǎn)化為

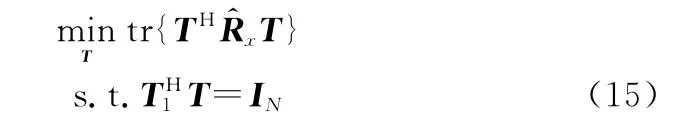
根據(jù)式（15）可以求得，轉(zhuǎn)換矩陣的表達式為

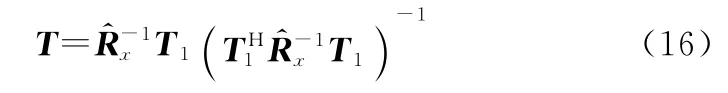
因此，波束空間信號數(shù)據(jù)（）和導向矢量（）可以表示為

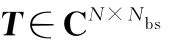
BS-GSC的其他變量可根據(jù)傳統(tǒng)GSC原理求解，BSGSC框圖如圖2所示。

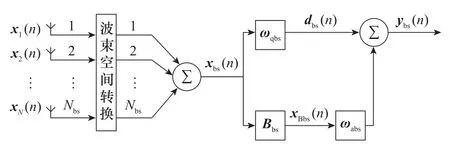
圖2 BS-GSC結構框圖Fig.2 Structural block diagram of BS-GSC

BS-GSC具體流程如下。

由式（16）確定轉(zhuǎn)換矩陣，通過轉(zhuǎn)換矩陣將陣元域信號數(shù)據(jù)（）和陣列響應矢量（）轉(zhuǎn)換到波束空間，求得波束空間信號數(shù)據(jù)（）和陣元響應矢量（）；

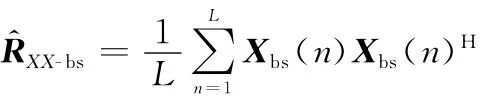
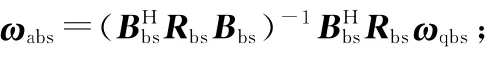
根據(jù)信號相消原理＝-，求得GSC的最佳權矢量。

2.2 基于粒子群的BS-GSC算法

本節(jié)針對廣義波束旁瓣相消器在低快拍情況下出現(xiàn)的不收斂和波束形成性能較差的問題，結合變換域原理，對信號數(shù)據(jù)進行全局搜索。在標準粒子群的算法基礎上，通過引入壓縮因子來加快粒子群的收斂性。

PSO是一種群智能算法，主要通過粒子間尋優(yōu)與更新的迭代手段求得最優(yōu)解。粒子的好壞由適應度函數(shù)來評價，在搜索解的過程中，每一個粒子都具有一組權值l 和一組權值更新速度向量v ，通過對粒子的權值與權值更新速度進行更新來得到最優(yōu)解。本文通過PSO算法，以BS-GSC的自適應權矢量為變量，以輸出最小均方誤差為適應度函數(shù)、以輸出最小均方誤差為目標尋取最優(yōu)解。定義適應度函數(shù)為

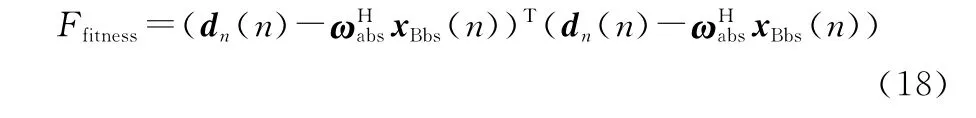
在空間內(nèi)隨機設置個粒子，進行第次迭代后，第個粒子的權值和權值更新速度分別為

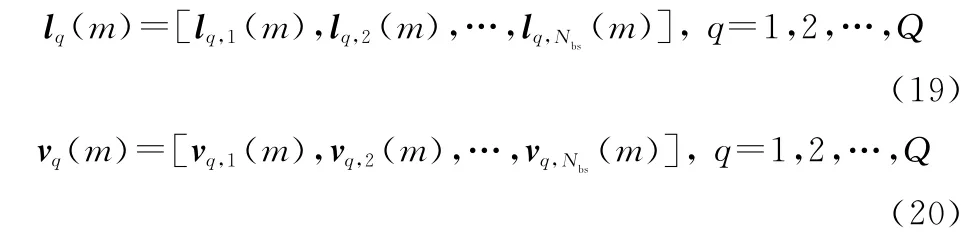
經(jīng)過次迭代后，粒子的權值和權值更新速度均是經(jīng)過多次優(yōu)化的結果。繼續(xù)迭代時，粒子會在自身的鄰域內(nèi)尋找適應度函數(shù)最佳的權值，并將鄰域內(nèi)的最優(yōu)點與粒子局部最優(yōu)點進行比較，將適應度函數(shù)最小的點作為粒子局部最優(yōu)點，即

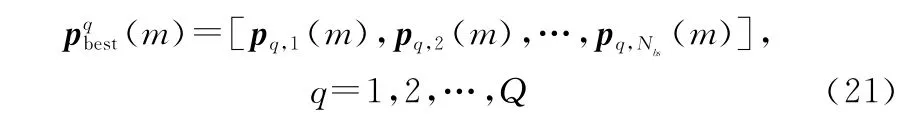
更新局部最優(yōu)點后，比較所有粒子的局部最優(yōu)點，并將適應度函數(shù)最小的點設為全局最優(yōu)點，即

同時也增強了算法局部搜索能力，壓縮因子粒子群算法權值更新速度和權值更新公式如下所示：

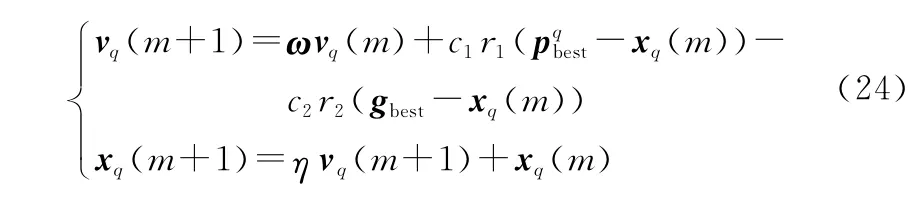
式中：表示壓縮因子。

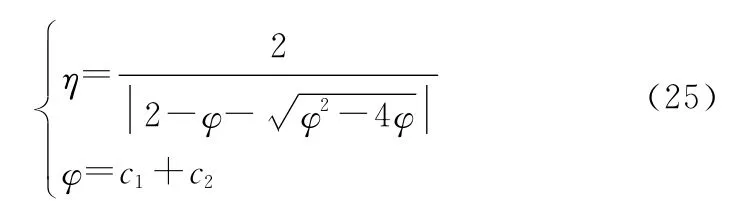
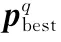
2.3 算法流程

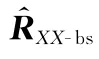
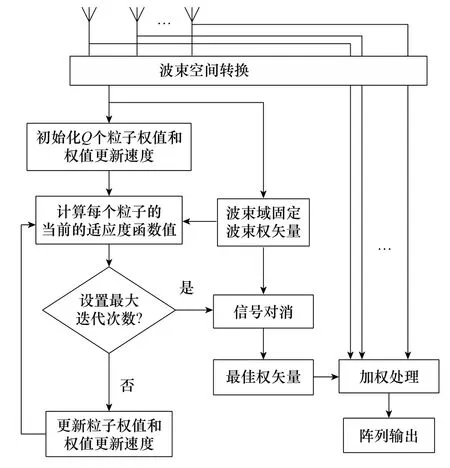
圖3 基于PSO的BS-GSC框圖Fig.3 Block diagram of BS-GSC based on PSO

在PSO算法中，設定每個粒子的維度與正交波束數(shù)量相同，粒子權值即為陣列權值，當循環(huán)次數(shù)達到最大迭代次數(shù)時算法終止，最大迭代次數(shù)通常與粒子數(shù)有關，粒子數(shù)量越大，算法收斂所需迭代次數(shù)越少。根據(jù)上述流程，本文算法計算步驟如下。

設定陣元數(shù)量為，快拍數(shù)為，正交波束數(shù)量為。

確定轉(zhuǎn)換矩陣與陣元接收數(shù)據(jù)矩陣相乘得到波束空間信號接收數(shù)據(jù)（）。

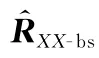
初始化粒子群，給定粒子群規(guī)模和循環(huán)次數(shù)，隨機產(chǎn)生粒子初始權值l 和權值更新速度v ，其中粒子權值由波束空間自適應權矢量代替。

計算各粒子當前的適應度函數(shù)。

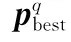
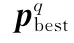
根據(jù)迭代次數(shù)重復步驟5～步驟7，輸出最后一次的全局最優(yōu)值，作為BS-GSC的自適應最優(yōu)權系數(shù)。

據(jù)信號相消原理＝-，求得GSC的最佳權矢量。

計算陣列的輸出（）。計算公式如下：

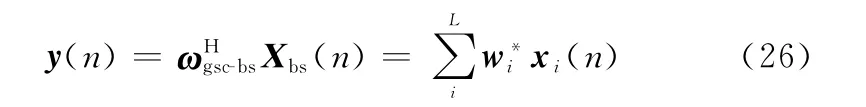
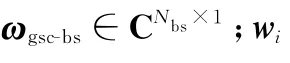
2.4 運算量和復雜度分析

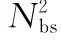
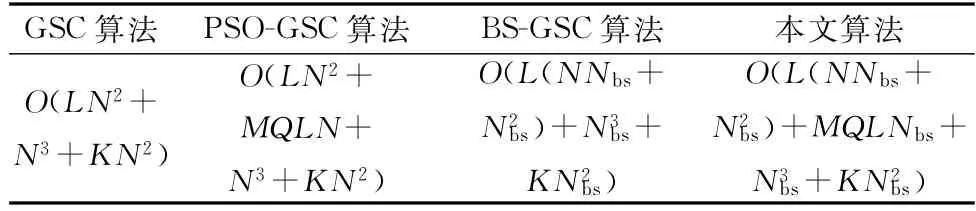
表1 算法運算量對比Table 1 Algorithm computation comparison

由表1可知，本文算法所在的波束空間相比于GSC和PSO-GSC的陣元空間（?）數(shù)據(jù)維度減小，算法的自由度降低，算法的運算量和復雜度均減小，由于本文算法的所有運算都是在波束空間進行，因此整體運算量要小于以上兩種算法，進行大規(guī)模陣列運算時實時性更好。由于本文算法采用粒子群尋優(yōu)手段求取最優(yōu)權值需要進行次迭代更新，運算量高于BS-GSC算法，但PSO算法采用最小均方誤差準則迭代尋優(yōu)，相對簡單，算法復雜度較低。

3 算法仿真與分析

使用Matlab軟件對本算法進行仿真模擬，原始數(shù)據(jù)為：陣元數(shù)＝30，正交波束數(shù)量＝10，期望信號角度＝10°，干擾信號角＝20°，＝-20°，＝60°，＝-60°，粒子數(shù)為500，迭代次數(shù)為100，設定目標信號為帶寬30 M Hz、中心頻率為50 MHz的線性調(diào)頻信號，干擾和噪聲均為高斯白噪聲。令信噪比（signal to noise ratio，SNR）為-10 dB，干噪比（jammer to noise ratio，JNR）為10 dB，快拍數(shù)＝500。在上述條件下進行仿真分析。

3.1 陣列響應性能

圖4的均勻線陣三維視圖展示了陣列響應增益與快拍數(shù)和角度的關系。可以看出，本文提出算法的波束形成的主方向0°的陣列幅度為0 dB，可以精準地指向期望來波信號的方向，并在干擾方向產(chǎn)生了陣列幅度小于-120 dB的零陷，在4個干擾方向均形成了較深的零陷。通過陣列響應增益隨快拍數(shù)的變化，可以看出本文算法雖然在極低快拍下會出現(xiàn)波形畸變的現(xiàn)象，但快拍數(shù)為20時，已經(jīng)具有了良好的波束形成能力，因此本文算法在整體上具有良好的波束形成效果。

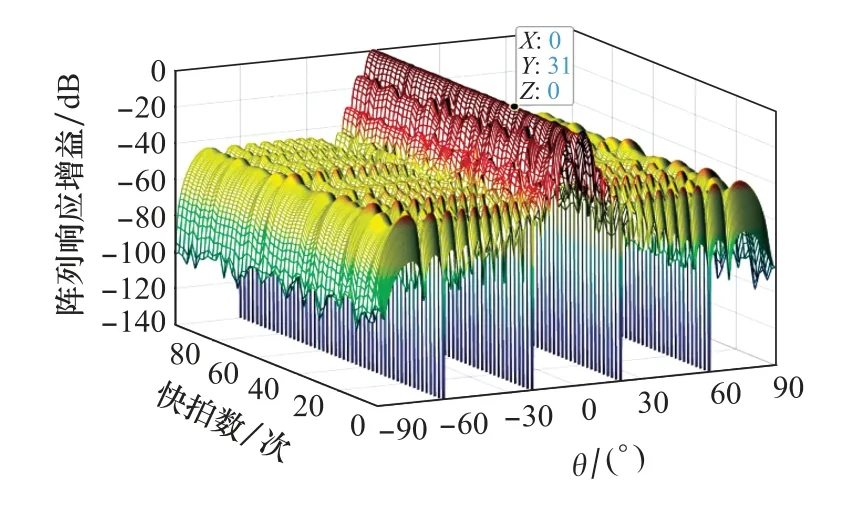
圖4 均勻線陣三維波束圖Fig.4 Three-dimensional beam pattern of uniform linear array

圖5將本文算法與GSC、PSO-GSC和BS-GSC算法進行對比。可以看出，4種算法均在期望方向上形成了主瓣，且主瓣寬度近乎相同。其中，本文算法具有更低的旁瓣，主要是由于構造轉(zhuǎn)換矩陣時，采用最小輸出功率準則，自適應調(diào)整轉(zhuǎn)換矩陣，在保證期望方向信號的增益不變的同時，使總輸出功率降低，從而降低波束旁瓣。并且，本文采用PSO算法和最小均方誤差準則，通過粒子的迭代更新逐漸縮小與期望信號的誤差，進一步降低了波束旁瓣。

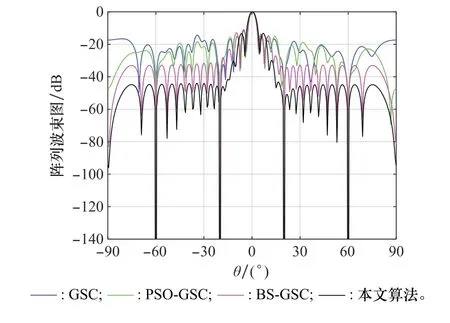
圖5 波束形成對比圖Fig.5 Comparison of beamforming

3.2 正交波束數(shù)量對本文算法的影響

在其他條件不變的情況下，將正交波束數(shù)量由8增加到17，得到波束形成方向圖，如圖6所示。由圖6可以看出，隨著正交波束數(shù)量的增加，波束的旁瓣略有降低，這主要是由于當波束數(shù)量增加時算法的自由度增加，使得算法的精度更高，效果更好。但是自由度的增加也會使算法的復雜度和運算量增加，因此確定正交波束數(shù)量時要選擇合適的值。

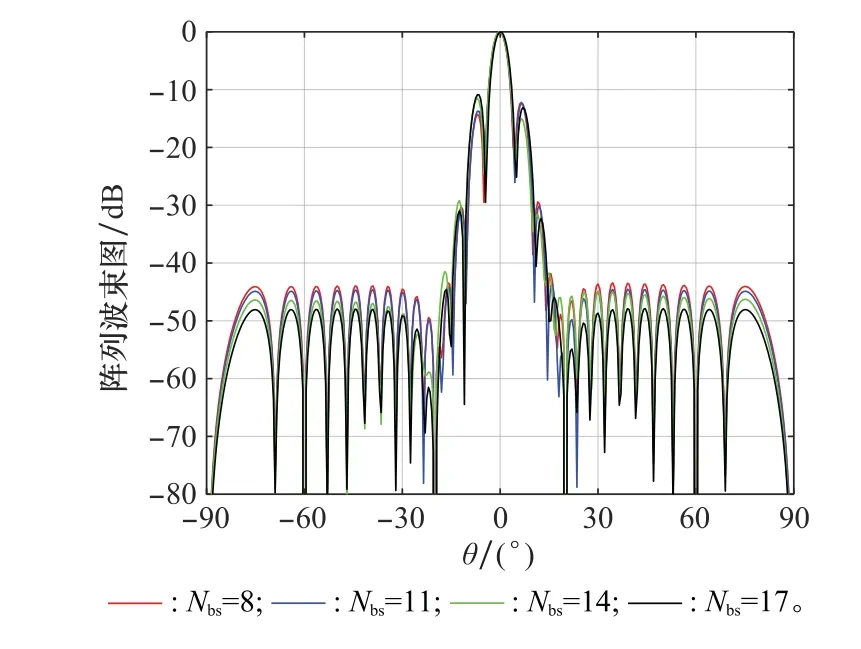
圖6 本文算法在不同正交波束下的波束方向圖Fig.6 Beam pattern of the proposed algorithm under different orthogonal beams

3.3 抗干擾性能分析

在其他條件不變的情況下，將JNR由-10 dB增加到150 d B，得到波束形成方向圖，如圖7所示。

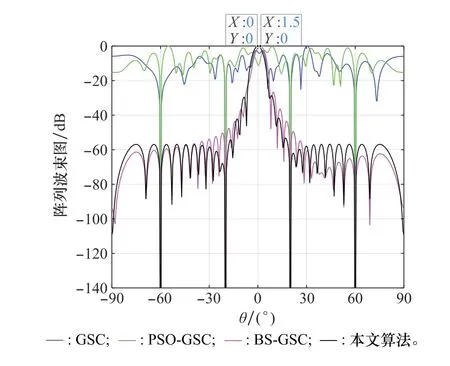
圖7 JNR為150 dB時4種算法波束方向圖Fig.7 Beam patterns of four algorithms when the JNR is 150 d B

由圖7可以看出，當JNR增加時，4種算法的性能都會受到影響。由于干擾功率過強，GSC和PSO-GSC算法已經(jīng)無法在期望方向上形成主瓣，BS-GSC算法可以正常形成主瓣但出現(xiàn)了1.5°的角度偏差。本文算法雖然主瓣變寬，但是仍可以在期望方向形成主瓣，可見在波束空間應用PSO算法，可以獲得更好的干擾抑制效果。

在保持上述條件不變的前提下，設置JNR的區(qū)間為［-30，150］d B，對4種算法求解均方誤差，得到圖8所示的均方誤差隨JNR的變化曲線。由圖8可以看出，4種算法在JNR低于140 dB時，均方誤差穩(wěn)定震蕩；當JNR大于140 dB時，GSC均方誤差隨JNR的增加而迅速增加，其他3種算法的均方誤差幾乎保持不變；總體上看，BS-GSC和本文算法的均方誤差值較小，PSO-GSC算法的均方誤差略高于此兩者算法。

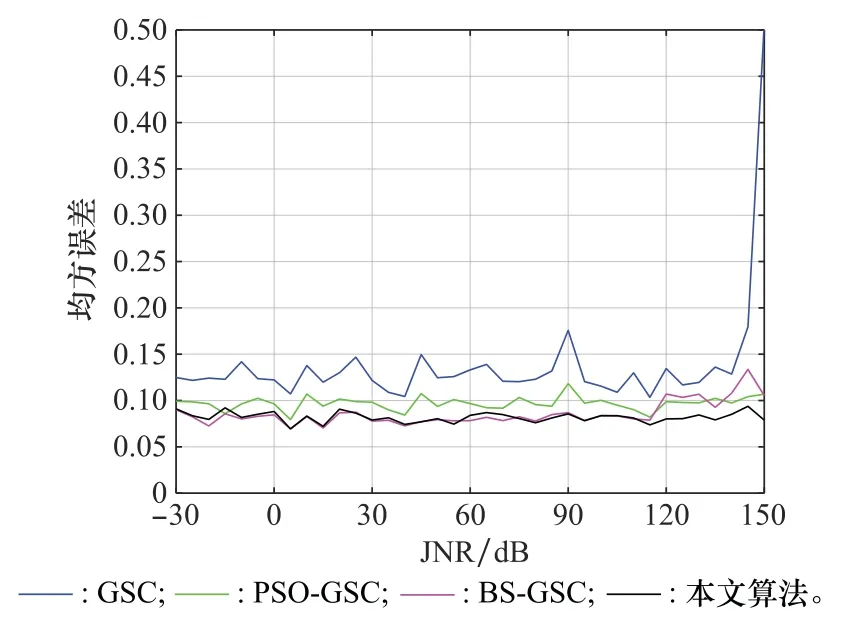
圖8 不同JNR對4種算法影響Fig.8 Influence of four algorithms with different JNRs

為更好地探究快JNR對本文算法的影響，取JNR分別為0 d B、30 dB、60 dB、90 dB、120 d B，其他條件與上述一致，得到波束方向圖如圖9所示。

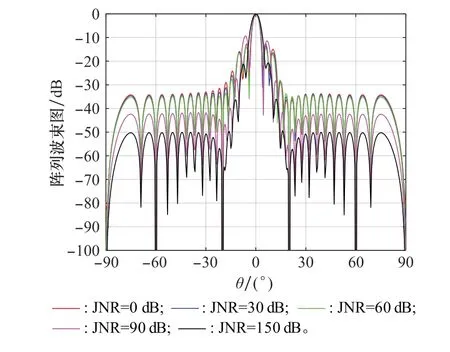
圖9 本文算法在不同JNR下的波束方向圖Fig.9 Beam pattern of the proposed algorithm under different JNRs

由圖9所示，本文算法波束形成方向圖的旁瓣隨JNR增加而降低，但當JNR過大時，由于干擾功率過強，導致波束形成方向圖的主瓣寬度增加，波束形成性能下降，信號的角度分辨率下降。總體上看，本文算法具有較好的抗干擾性能。

3.4 SNR對算法的影響

在其他條件不變的情況下，將信號的SNR由-10 dB增加到10 d B，得到波束形成方向圖如圖10所示。由圖10可以看出，當SNR增加時，4種算法的性能都會受到影響，GSC、PSO-GSC、BS-GSC算法已經(jīng)無法在期望方向上形成主瓣，這主要是由于當SNR增加時，期望信號的功率較大，導致阻塞矩陣不能完全阻塞期望信號，從而導致期望信號對消的現(xiàn)象。而本文算法雖然主瓣變寬，但是仍可以在期望方向形成主瓣，可見本文算法在抑制期望信號對消方面也有較大優(yōu)勢。

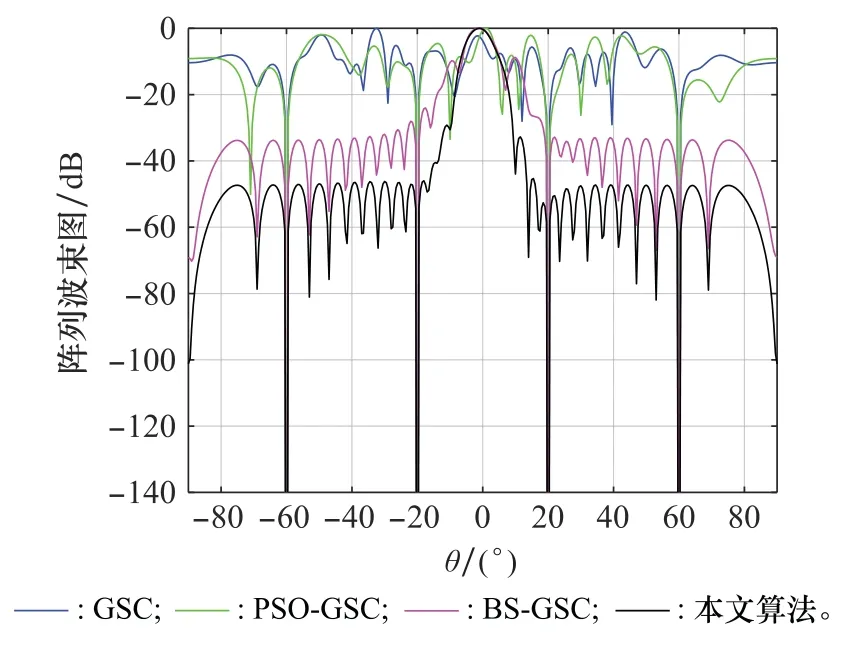
圖10 SNR為10 dB時4種算法波束方向圖Fig.10 Beam pattern of four algorithms when the SNR is 10 dB

在保持上述條件不變的前提下，設置SNR的區(qū)間為［-10，30］dB，對4種算法求解均方誤差，得到如圖11所示的均方誤差隨SNR的變化曲線。由圖11可以看出，4種算法在SNR低于15 d B時，均方誤差趨于零且平穩(wěn)；當SNR在［15，25］dB時，GSC和PSO-GSC算法的均方誤差隨SNR的增加而增加，其他兩種算法的均方誤差幾乎保持不變；當SNR大于25 dB時，4種算法的均方誤差均隨SNR增加而增加，GSC算法的均方誤差增加得最快，PSO-GSC算法其次，BS-GSC算法和本文算法均方誤差最小且增加速度相當。

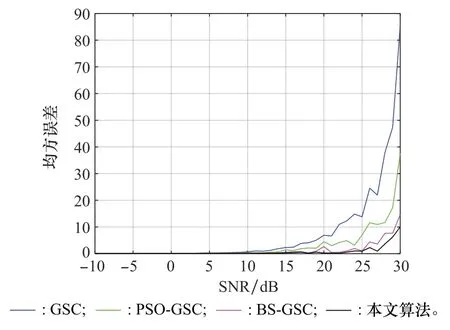
圖11 不同SNR對4種算法影響Fig.11 Influence of four algorithms with different SNRs

為更好地探究SNR對本文算法的影響，取SNR為-20 dB、-10 dB、0 dB、10 d B、20 d B，其他條件與上述一致，得到波束方向圖如圖12所示。由圖12所示，本文算法在SNR小于10 d B時，可以在期望信號方向形成主瓣。當SNR為20 d B時，由于期望信號相消導致無法在期望信號方向形成主瓣。由此可以看出，本文算法在一定程度上可以抑制期望信號相消，當SNR過大時，算法的波束形成性能會惡化。

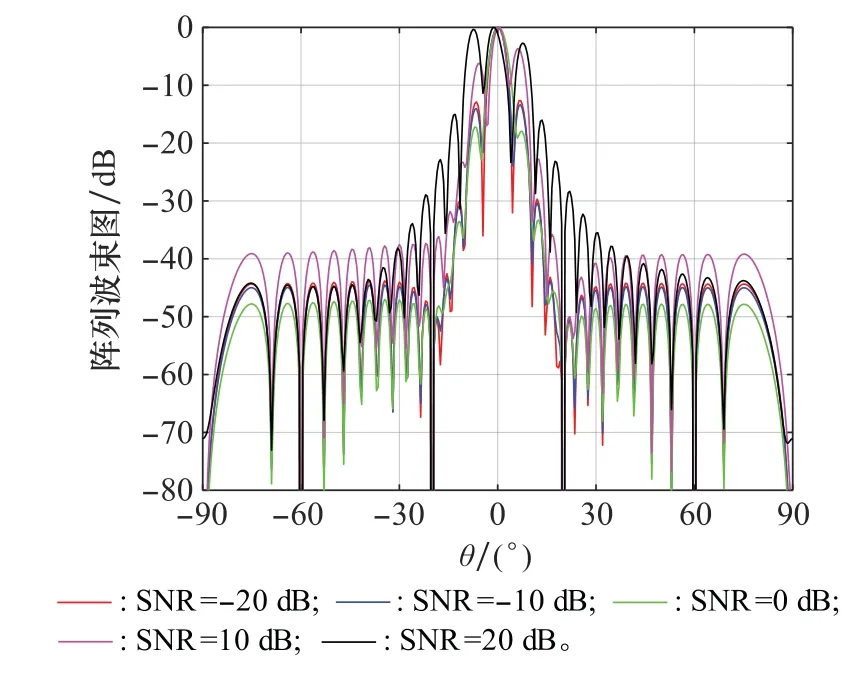
圖12 本文算法在不同SNR下的波束方向圖Fig.12 Beam pattern of the proposed algorithm under different SNRs

3.5 快拍數(shù)對算法的影響

在其他條件不變的情況下，將快拍數(shù)設定為20，得到波束形成方向圖如圖13所示。

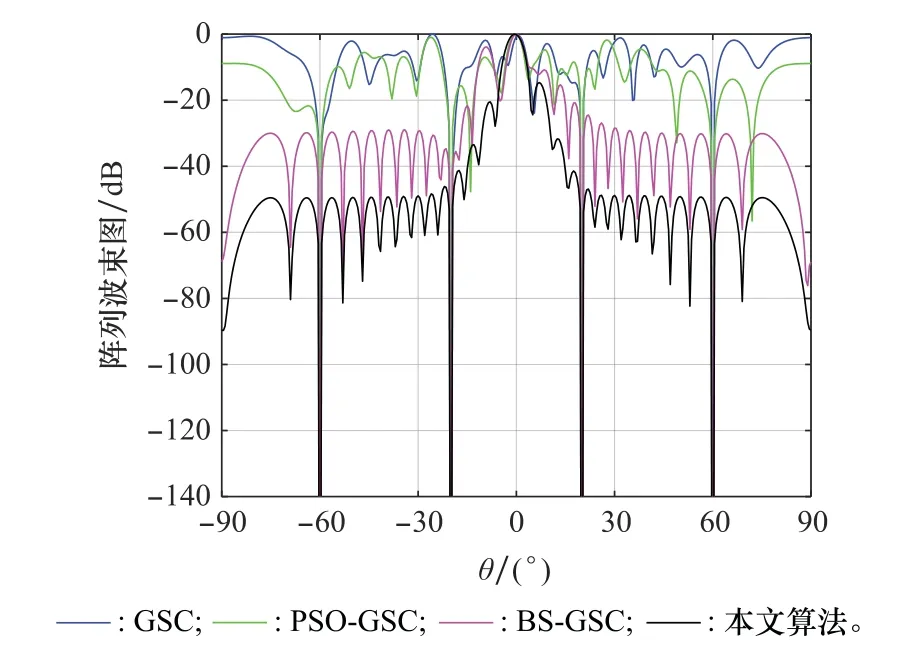
圖13 快拍數(shù)為20時4種算法波束方向圖Fig.13 Beam pattern of four algorithms when snapshot number is 20

由圖13可以看出，在低快拍情況下，GSC算法已經(jīng)無法在期望方向形成主瓣，波束方向圖出現(xiàn)嚴重惡化，PSOGSC算法和BS-GSC算法可以正常形成主瓣，但是旁瓣電平升高，波束形成性能變差，導致虛警概率升高。本文算法依舊可以形成正常主瓣，但是主瓣寬度略有增加，旁瓣電平保持不變。由上可知，在低快拍的條件下，本文算法的期望信號波束指向和旁瓣抑制性能較好。

在保持上述條件不變的前提下，設置快拍數(shù)的區(qū)間為［0，400］，對4種算法求解均方誤差，得到如圖14所示的均方誤差隨快拍數(shù)的變化曲線。由圖14可以看出，4種算法的均方誤差數(shù)值均隨快拍數(shù)的增加而減小，其中傳統(tǒng)GSC算法的均方誤差大于其他3種算法。BS-GSC和本文算法的均方誤差較小，在低快拍的條件下本文算法均方誤差小于BS-GSC算法，當快拍數(shù)較高時，兩種算法的均方誤差數(shù)值趨于穩(wěn)定且相近。

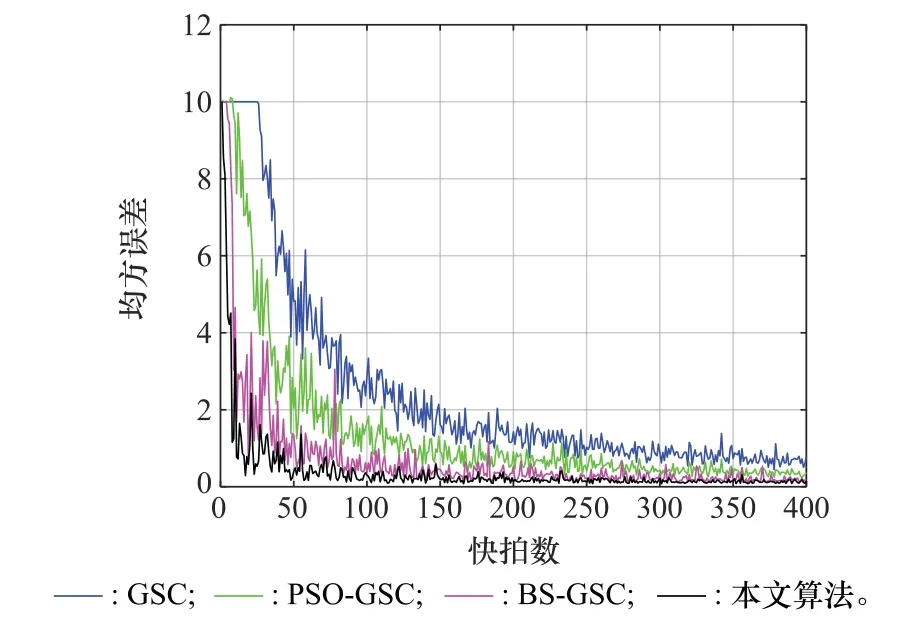
圖14 不同快拍數(shù)對4種算法影響Fig.14 Influence of different snapshot numbers on four algorithms

為更好地探究快拍數(shù)對本文算法的影響，取快拍數(shù)分別為10、30、60、100、200，其他條件與上述一致，得到波束方向圖如圖15所示。

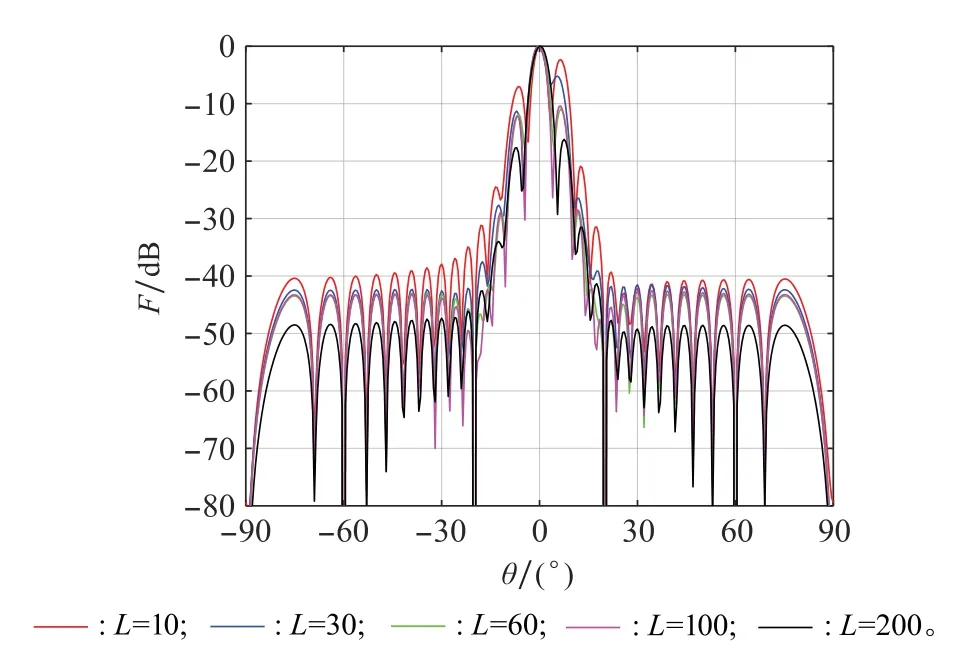
圖15 本文算法在不同快拍數(shù)下的波束方向圖Fig.15 Beam pattern of the proposed algorithm under different snapshot numbers

由圖15可以看出，本文算法的旁瓣隨著快拍數(shù)的增加逐漸降低，當快拍數(shù)為10時，旁瓣電平相對偏高，但仍然可以在期望信號方向形成主瓣，并且隨著快拍數(shù)的增加波束旁瓣逐漸降低。可見本文算法在低快拍的情況下，依舊可以保持良好的波束形成能力。

3.6 來波方向?qū)λ惴ㄐ阅艿挠绊?/h3>

在其他條件不變的情況下，將信號的來波方向分別調(diào)整為：期望信號角度＝0°，干擾信號角＝3°，＝-5°，＝5°，＝-3°和期望信號角度＝0°，干擾信號角＝5°，＝-5°，＝10°，＝-10°，由圖16和圖17可知，當干擾方向與期望信號方向較近時，4種算法可以在期望方向形成主瓣，但當干擾進入主瓣方向時，4種算法均無法在期望信號方向形成主瓣，因此本文算法的抗主瓣干擾能力仍需提高。

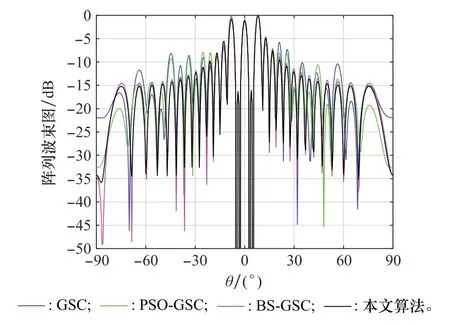
圖16 來波方向為0°、3°、-5°、5°、-3°時波束方向圖Fig.16 Beam pattern when the incoming wave direction is 0°，3°，-5°，5°，-3°

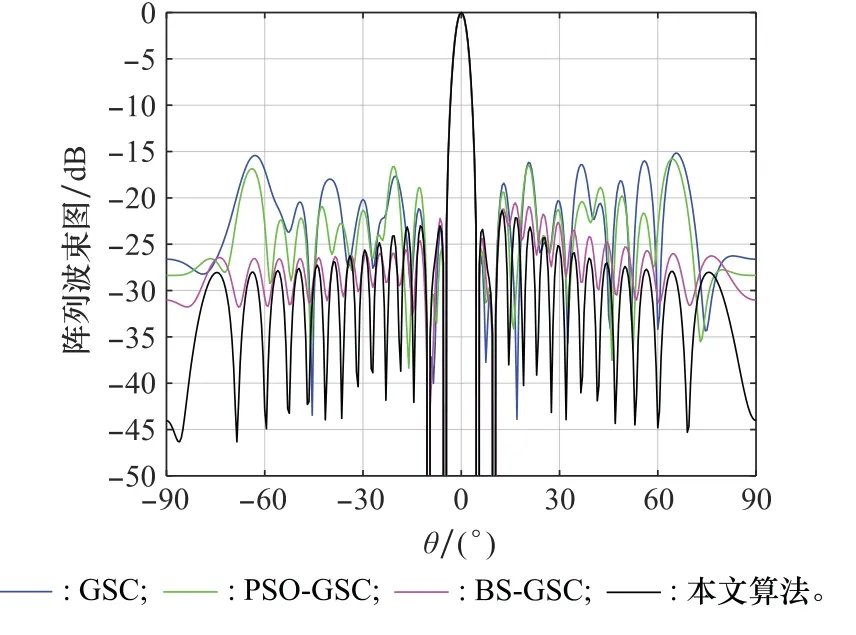
圖17 來波方向為0°、5°、-5°、10°、-10°時波束方向圖Fig.17 Beam pattern when the incoming wave direction is 0°，5°，-5°，10°，-10°

由圖18可知，當SNR小于10 dB時，4種算法的輸出SINR均隨SNR增加而近似線性增加，且輸出SINR的值較為相近；當SNR在［10，30］dB時，GSC和PSO-GSC算法出現(xiàn)飽和，其他兩種算法輸出SINR隨SNR增加而增加；當SNR大于30 d B時，本文算法輸出SINR隨SNR增加而緩慢增加，BS-GSC算法則出現(xiàn)緩慢下降的趨勢。總體上看，本文算法的輸出SINR相比于其他3種算法均有提高，因此在保持其他條件穩(wěn)定不變的情況下，本文算法的輸出形成優(yōu)于其他3種算法。

3.7 輸出性能分析

將快拍數(shù)設定為400，令SNR從-40 d B增加到70 dB，其他條件保持不變，比較4種算法輸出信干噪比（signal to interference plus noise ratio，SINR）與輸入SNR的變化關系，結果如圖18所示。

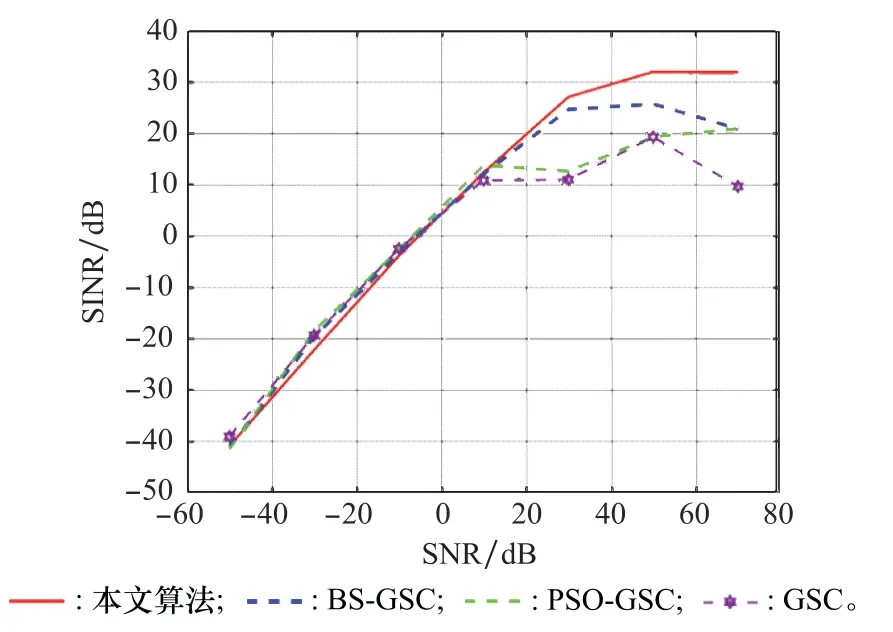
圖18 4種算法輸出SINR隨輸入SNR的變化曲線Fig.18 Variation curve of output SINR of four algorithms with input SNR

4 結 論

本文基于傳統(tǒng)GSC算法工程應用廣泛的實際，針對GSC運算量過大、波束旁瓣較高、在低快拍條件下波束形成效果不理想的問題，提出了一種基于PSO算法的BS-GSC算法。本文算法采用一種高效的自適應轉(zhuǎn)換矩陣方法，將接收數(shù)據(jù)由陣元空間轉(zhuǎn)到波束空間，以降低算法的自由度為前提并有效減少了運算量。同時，利用粒子群尋優(yōu)手段充分挖掘信號數(shù)據(jù)的相關性，并引入壓縮因子的概念增強算法的局部搜索能力，增強了算法的穩(wěn)健性。仿真結果表明，本文算法在強干擾和低快拍的條件下，仍具有良好的波束形成能力，并有效改善了期望信號對消的現(xiàn)象。