針對無人潛航器的反潛策略研究

曾 斌，張鴻強，李厚樸

（1.海軍工程大學管理工程與裝備經濟系，湖北 武漢 430033；2.海軍工程大學導航工程系，湖北 武漢 430033）

0 引 言

無人潛航器（unmanned underwater vehicles，UUV）具有長期水下自主航行能力，經常用于在水下執行搜集艦艇聲紋、偵察與監視、反潛警戒、探測海底地勢和資源等各類任務［1-2］。近年來，在很多重要海域經常發現UUV的出沒，疑似用于搜集我方艦艇信息、海上實驗數據以及重要海域的水文情報［3］，甚至日本在2018年12月新版的《防衛計劃大綱》中公開宣布計劃在釣魚島等海區部署新型UUV，這些對我國海洋國土安全構成極大威脅［4］，因此針對敵方UUV入侵的反潛方法研究日益重要。

UUV入侵與潛艇入侵相比有幾點不同：體積小，噪聲低，隱蔽性更強；經常多艘同時入侵；可用于長時間自主監測，且具有一定反搜索能力；具有軍民難分的特點，法律地位模糊［3-4］。這就導致針對UUV入侵的反潛作戰更為困難。針對潛艇的常規反潛行動需要通過派遣反潛巡邏機或直升機等手段搜潛，判斷出潛艇的初始位置，然后在一個預估范圍內展開搜索［5-6］。而UUV隱蔽性更強，許多情況下只是根據不確定的情報線索，例如漁民報告或聲納網絡的疑似預警，懷疑有不明水下裝置在我方利益區域（例如海上試驗區、關鍵航道或油氣田區）活動，由于缺少明確定位，起始搜索范圍較大。同時針對多艘UUV情況，我方搜潛平臺還需要協同工作，這更加大了反潛難度。另外，利用反潛巡邏機和直升機進行UUV搜潛的費效比也較低，而利用UUV偵搜UUV更加可行，這就要求反潛UUV能夠自主探測、協同并跟蹤敵方UUV。

從公開文獻看，除了一些非正式的網上相關報道，尚未查找到專門針對UUV的反潛研究學術性論文，但針對潛艇的反潛研究一直是研究熱點。例如，上下文感知的反潛任務決策支持方法［7］利用隱馬爾可夫模型對反潛資源分配和搜索路徑規劃問題進行了數學建模，并采用進化算法對數學模型求解。隨機反潛巡邏算法［8］認為利用現有技術難以在開放海域偵搜潛艇，為此提出在被島嶼等地形限制潛艇行動的海域進行巡邏監測的路徑規劃算法。反潛資源優化部署算法［9］把反潛任務看作有限時間范圍內的零和博弈，并利用線性規劃算法求解出優化策略。反潛規劃輔助工具［10］針對分布在多海域的多個反潛任務，利用線性規劃對不同類型的反潛裝備分配問題進行了建模和求解。文獻［11］對文獻［10］的線性規劃模型進行了擴展，加入了時限參數。但以上反潛研究都是以數學規劃模型作為理論基礎，適用于只有單個水下目標（一個潛艇）的確定性環境。

另外，近年來博弈論、深度強化學習等方法在國土安全的資源調度領域日益得到重視。例如，文獻［12］基于博弈論建立了攻防資源分配模型。文獻［13］針對海岸安全巡邏問題，基于量子反應模型對敵方目標進行行為建模，利用攻防Stackelberg博弈模型設計了海岸巡邏調度算法。文獻［14］把強化學習引入到多人博弈中，并提出了軟團隊（actor-critic，AC）算法求解團隊協作問題。文獻［15-16］提出了深度虛擬博弈算法求解環保領域的資源分配問題。盡管這些研究更多的是關注陸地上安保資源的分配及巡邏問題，與反潛規劃有較大差異，但從中可以看出機器學習、多智能體學習等新興技術在博弈論領域能夠解決某些傳統線性規劃算法難以計算的問題。

為此，本文設計了一個兩階段反潛規劃算法。提出了基于強化學習AC算法（actor-critic，AC）的魯棒性部署策略學習算法，用以計算不確定環境下的資源部署問題；提出了基于多智能體強化學習的搜潛策略學習算法，用以計算團隊攻防環境下的搜潛路徑規劃問題。針對敵方目標噪聲低和具有自主行為模式的特點，在強化學習的馬爾可夫決策模型中加入了綜合反映聲納探測概率和海區重要度的獎勵值設計；針對不確定的敵方目標分布情況，在強化學習中引入參數擾動機制提高算法的魯棒性。由于本文反潛算法不僅適用于UUV，同樣也能用于常規潛艇，所以后文敵方目標通稱為水下探測器。

1 反潛問題的指標設計

假設反潛海域劃分為I個網格區域或分區，每個網格可看作一個包含深度的長方體，符號i＝｛1，2，…，I｝表示反潛分區的計數下標，反潛指揮人員可以按照優先級定義每個反潛區域的重要性，用ui表示。反潛博弈過程包括J＋K個運動物體，其中包含J個敵方水下目標和K個我方搜潛平臺，符號j＝｛1，2，…，J｝表示水下目標的下標，k＝｛1，2，…，K｝表示我方搜潛平臺的計數下標，敵方水下目標和我方搜潛平臺作為多智能體運行。反潛的目標是：通過我方搜潛平臺智能體的分工協作，在降低我方重要反潛海域威脅度的同時，提高對敵方水下目標的檢測率。

首先定義威脅度指標，表示j號敵方目標對i號分區的威脅程度，用TIij表示。設Dist（i，j）表示j號目標與i號分區之間距離，則當Dist（i，j）越大且i號分區重要性u i越小時，威脅度越低，所以TIij定義如下：

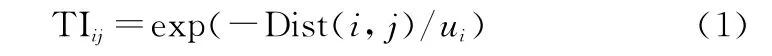
第2個指標為目標探測率。復雜多變的海洋環境會產生水下聲波傳播的功率損耗，其中回波、環境噪聲等都會極大地影響搜潛平臺聲納系統的傳感性能［17］。搜潛常用的主動聲納的聲信號流程為：換能器陣發出聲波，通過海水傳播至目標，在目標物產生散射／反射，經過海水傳至接收換能器陣，其探測方程如下：

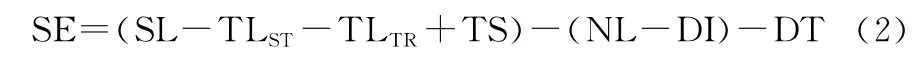
式中：SE（以dB為單位）表示信號余量，作為聲納探測性能的指標；SL為聲納級別，表示聲納發射器發出的聲波量；TLST和TLTR分別表示從聲源（搜潛聲納）至水下目標和從水下目標至聲源之間的傳輸損耗；TS為目標強度，表示目標物反射／散射的能力；NL表示周圍海洋環境的噪聲級別；DI和DT分別表示方向性增益和檢測閾值。

在此基礎上，為了反映聲納探測的不確定性，本文利用概率模型計算搜潛聲納探測水下目標的能力。該模型同樣適用于被動聲納方程。

當第k個搜潛平臺獲得的第j個水下目標的回波信號余量為SEjk時，定義第k個搜潛平臺對第j個水下目標的探測概率為

式中：Φ是正態分布概率函數；σ為標準差，一般取3～9 dB之間［7］。當不考慮聲納、環境和目標的隨機性時，P jk僅為j號敵方目標和k號搜索平臺之間距離的函數。

2 部署策略的學習

本文把搜潛攻防過程劃分為兩個階段。第1個階段為資源分配，在這個階段我方把搜潛平臺部署到不同的網格分區，這也代表了搜潛開始時的起始位置。對應地，敵方也在這個階段部署不同數量的水下探測器至對自己占優的網格海區。第2個階段為搜潛階段，在這個階段敵方水下探測器在我方反潛海域活動，試圖探測甚至攻擊我方重要設施，而我方搜潛平臺則需要在保護我方重要海域的同時搜索破壞敵方水下探測器目標。

本節描述部署階段敵我雙方攻防博弈采用的分配策略。

2.1 資源分配模型

分配模型基于不確定性馬爾可夫決策過程［18］建立，利用四元組［S d，A d，T d，R d］表示。狀態S d＝［a t-1，u t-1］，a t-1表示我方在t-1時間段的動作，為資源分配方案矢量，表示每一個反潛分區內指派的搜潛平臺數量，總數量小于等于我方搜潛平臺資源總量，例如a＝（2，1，2，0，0）表示在第1～第3號反潛分區指派搜潛平臺數量分別為2、1、2，其他分區沒有分配資源。u t-1表示t-1時間段的各個反潛分區重要性，該狀態分量用于描述我方保護目標位置變化的場景。A d表示敵我雙方的博弈動作空間，由資源分配方案矢量構成。狀態遷移T d：S d→與敵方目標的位置參數相關，設l為敵方水下探測器的出現位置和數量，為不確定參數，敵方部署的混合策略πl將會生成狀態遷移T d上的一次概率分布，例如假設有兩個敵方目標可能出現的位置和數量矢量，l1＝（3，2，1，0，0）和l2＝（2，3，0，1，0），表達方式同資源分配矢量，本文稱之為目標分布矢量，如果πl＝（0.6，0.4），表示l1有0.6的概率出現，l2有0.4的概率出現，狀態遷移的混合策略分布是不確定性馬爾可夫決策過程的主要特征。

在具體實現時，為了提高強化學習的效率，本文把方案矢量或分布矢量映射為［0，1］之間的小數，在應用時通過Lambda函數把連續小數還原為數量。另外，為了表達搜潛平臺以及探測器的不同類型，可以把方案矢量以及分布矢量擴展為2維矩陣，第1維為反潛分區，第2維為裝備類型。

獎勵R d表示執行動作的獎勵，由第1節介紹的反潛指標構成，我方k號搜潛平臺的獎勵r k定義如下：

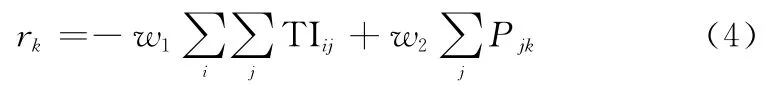
敵方j號探測器獎勵r j定義如下：

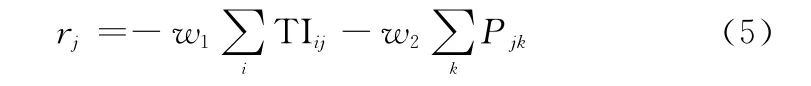
式（4）和式（5）中w1和w2表示組合指標權重。

2.2 魯棒性部署策略學習算法總體設計

敵方分布矢量l為不確定參數，我方對其分布也缺乏先驗知識，為此需要我方的部署策略πa對于不確定參數l具有一定魯棒性。本文采用了魯棒性決策理論中的最小最大后悔值方法［19］來設計魯棒性部署算法。設r（πa，l）為在敵方不確定性參數l影響下，我方采用策略πa所獲得的期望獎勵，則我方采用策略πa的后悔值定義如下：

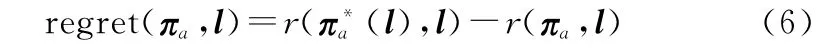
因此，部署算法的目標是計算得到我方部署策略πa，能夠最小化不確定參數l下的最大可能后悔值，利用式（6）可推導出該問題的規劃模型為

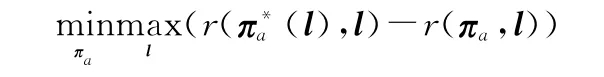
該規劃模型可以看作是敵我雙方的博弈問題，針對敵方選擇最壞情況下的參數值l，我方需要學習優化策略πa，最小化最大的后悔值，該博弈問題中，我方的收益為-regret，敵方收益為regret。借鑒double oracle算法、博弈論和深度學習思想，部署策略學習算法設計如下。

如果對敵方探測器的分布情況有歷史數據作為啟發線索，可以在算法輸入時作為參數集L輸入，否則可以隨機生成L。算法1中，第1行～第4行為初始化。從第5行開始進入敵我雙方博弈的外循環，第6行和第7行敵我雙方根據對手的方案集和策略，生成自己的最佳反應方案，第8行擴充現有方案集并計算雙方收益矩陣pm。如果不考慮擾動機制，最后利用收益矩陣計算納什均衡下的混合策略。

本文出于以下兩個原因引入了參數擾動機制：一是由于水下復雜環境的影響，我方聲納難以精確獲取敵方水下目標的分布情況；第二個原因與強化學習的精度有關，對于一個給定的敵方分布，我方強化學習機并不能保證一定得到最佳反應策略。因此，受獎勵值隨機擾動處理不確定參數的思路啟發，本文加入分布參數l的不同擾動值，便于我方學習機搜索優化策略（l）以及最佳反應方案。

另外，算法中博弈樹規模與反潛分區數量相關，計算復雜性屬于多項式范圍，能夠利用線性規劃（本文利用Nashpy庫函數［20］進行計算）求解出納什均衡解。所以，盡管參數擾動機制增加了更多的候選方案，但是只擴大了收益矩陣的大小，計算復雜性的增加幅度并不大。

下面為收益矩陣計算函數UpdatePayoffs的偽代碼。

下面描述敵我雙方最佳反應策略的學習算法。

2.3 最佳反應策略學習算法設計

我方最佳反應策略的學習算法為DefendPlanBR，在給定的敵方分布集S l和策略πl的情況下，學習我方部署優化策略πa，使得我方部署方案能夠最大化獎勵值。該算法直接采用了強化學習的深度確定性策略梯度（deep deterministic policy gradient，DDPG）架構［21］來獲取優化的部署策略。DDPG架構可以看作AC架構［22］和深度Q網絡（deep Q network，DQN）［23］的綜合，能夠解決連續性動作問題。

敵方最佳反應策略的學習算法為Enemy Plan BR，與我方學習算法DefendPlanBR類似，也是采用了DDPG算法架構，但因為需要同時計算敵方水下探測器的分布策略πl和不確定參數l，所以算法更加復雜。

最為直接的方法是采用兩套學習機（AC神經網絡）分別訓練πl和l，但是由于不確定參數l和策略πl強相關，這種分離式訓練方法只能得到次優結果，因此本文采用喚醒-休眠機制，利用1套AC神經網絡同時優化πl和l，不僅能夠簡化算法復雜性，而且提高了訓練速度，算法偽代碼如下。

EnemyPlanBR偽代碼中，為了提高算法魯棒性，第3行利用隨機抽樣生成新的部署策略，第5行～第7行在實現時可以利用Tensor Flow或Py Torch的選擇性權重梯度求解接口實現，第8行需要利用第3節搜索訓練好的敵我雙方攻防策略計算下一步時間段的獎勵和狀態結果，第10行調用了DDPG網絡的更新算法，為了偽代碼的表達清晰，省略了DDPG網絡的經驗回放和目標網絡更新等步驟。

3 搜潛策略的學習

3.1 搜潛模型的建立

部署階段考慮的是敵我雙方兩個指揮機構之間的零和博弈，而搜潛階段需要考慮多個智能體（多個我方搜潛平臺和多個敵方水下探測器）之間的協作與攻防關系，為此在搜潛階段采用了基于多智能體的部分可觀察馬爾可夫決策 過 程［24］（partially observable Markov decision processes，POMDP）來建立攻防模型。設系統內共有N個智能體（下標為n），環境的部分可觀察狀態空間定義為O＝｛O1，O2，…，O N｝，動作空間定義為A＝｛A1，A2，…，A N｝，對于我方搜潛平臺和敵方探測器，考慮到搜潛仿真軟件中探測概率的計算需要（見第1節），選取3個自由度方向的動力為動作，即動作a n為包含3個實數分量的矢量，水面艦船深度方向動力為0。在搜潛階段，假設敵我雙方只能感知自己傳感距離之內的環境和物體，我方搜潛平臺具有通信能力，且每個智能體按時間步長移動。對于我方搜潛平臺智能體，其狀態包括：搜潛網格分區中我方各個搜潛平臺的位置、深度、類型，搜潛平臺上聲納傳感器的觀測結果，某一個分區內是否檢測到敵方目標，搜潛平臺的通知消息、各個網格分區的重要性（如果保護對象為編隊等移動對象）以及每一個分區的經過次數等。敵方探測器的狀態包括：觀測范圍內我方和敵方UUV的位置信息。

獎勵函數R的定義與第2.1節資源分配模型相同。對于狀態轉移函數，每一個智能體包含一套AC網絡，其中actor網絡輸入矢量為局部觀察狀態On，每一個時間步長t，智能體n根據AC網絡中參數化的策略πl，選擇動作a n，并獲得獎勵rn，每一個智能體的目標是最大化其期望獎勵，其中γt為t時段的折扣率,為第n個智能體在時段t收集到的獎勵。

3.2 搜潛策略學習算法的設計

本文提出了一個基于多智能體DDPG［25］（multi-agent DDPG，MADDPG）的搜潛算法，用以學習我方搜潛策略，MADDPG是DDPG架構在多智能體學習方面的擴展，采用的是集中式訓練 -分布式執行學習模式［26］，這種模式特別適用于POMDP，由于搜潛過程中單個智能體都無法獲取整個環境的完整狀態信息，所以在訓練時給智能體的critic網絡以集中訓練形式提供額外信息，這樣可以幫助智能體學習到更好的動作策略。

設搜潛環境中包括K個搜潛平臺，策略空間πD＝｛π1，π2，…，πK｝，對應K個搜潛平臺智能體的actor神經網絡參數θ＝｛θ1，θ2，…，θK｝，另外設有J個敵方水下探測器，策略空間τE＝｛τ1，τ2，…，τJ｝，對應的actor神經網絡參數ψ＝｛ψ1，ψ2，…，ψK｝，則我方第k個搜潛平臺智能體的actor網絡參數的梯度更新公式如下：

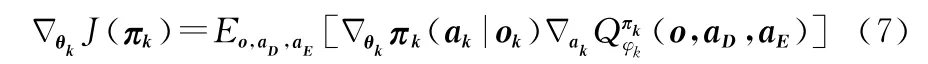
同樣，敵方第j個探測器智能體的actor網絡參數的梯度更新公式如下：

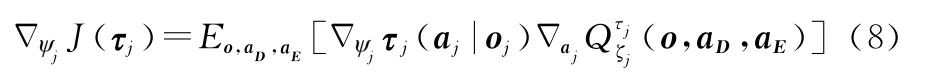
式（7）和式（8）中o＝｛o1，o2，…，o K＋J｝表示敵我雙方的可觀測狀態；ak表示我方第k個搜潛平臺的動作，a D＝｛a k｝表示我方所有搜潛平臺的動作；a j表示敵方第j個搜潛平臺的動作；a E＝｛a j｝表示敵方所有探測器的動作，Q函數表示提供了所有環境信息（o，a D，a E）的集中動作 價值函數，它用于計算智能體的Q值，其中φk和ξj分別為我方和敵方智能體Critic網絡的權重參數。

我方第k個搜潛平臺智能體的Critic網絡參數的梯度更新公式如下：

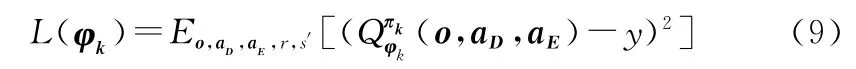
敵方第j個探測器智能體的Critic網絡參數的梯度更新公式如下：

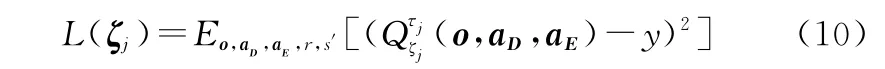
式（10）和式（11）中y的定義為

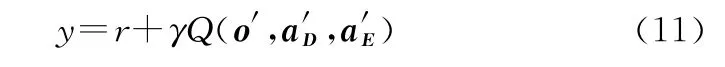
算法4為搜潛算法偽代碼，為簡潔起見，偽代碼只考慮了敵我雙方各擁有一種類型的裝備，如果需要考慮多種裝備，只需在算法中添加新類型裝備的智能體訓練流程即可。

算法分3個部分，第1部分從第4行到第14行，第6行從當前策略中隨機生成敵我雙方所有智能體的動作，數據類型為矩陣，并在第7行把這些動作輸入給搜潛過程仿真軟件，以矩陣形式返回下一時間步的各自狀態和獎勵，并在第8行至第13行把敵我雙方的當前狀態、下一步狀態、動作以及獎勵存入回放緩存。第1部分運行MAX_EP_STEPS個循環，得到一批可用于強化學習的數據集。

第2部分從第15行至第21行，主要用于我方所有搜潛平臺智能體搜潛策略的學習。第16行從回放緩存中采樣一批大小為N s的訓練樣本，17行～18行按式（11）生成y，第19行更新critic神經網絡權重，損失值計算是式（9）的具體實現，第20行更新actor神經網絡權重，梯度下降更新是式（7）的具體實現。

第3部分用于敵方所有水下探測器智能體入侵策略的學習，與第2部分類似。這里為了簡潔起見，省略了諸如固定目標網絡的賦值等細節。

4 仿真實驗結果分析

本文實驗程序利用Python開發，強化學習二次開發平臺為Tensor Flow［27］。由于在策略學習過程中需要調用反潛仿真軟件獲取訓練數據，為了與現有強化學習開發模式兼容，對現有反潛仿真軟件的接口進行了封裝，參照Open AI Gym工具庫的規范，實現了仿真過程的reset和step2個關鍵接口。

4.1 實驗采用的神經網絡結構

首先描述搜潛策略學習算法中智能體的神經網絡結構。actor網絡第1層和第2層為卷積層，卷積層之間采用非線性Re Lu函數激活。輸入層為卷積層結構，包括10個3×3的卷積核，步長為1×1；第2層也采用卷積層，包括20個3×3的卷積核，步長為1×1；第3層為包括128個隱藏節點的全連接層；第4層為包括64個隱藏節點的全連接層；第5層同樣為全連接層，包括3個單元，表示動作空間的3個維度；各層之間采用ReLu函數激活；最后為lambda層，通過tanh函數把動作范圍映射到對應的量綱。

搜潛策略學習算法中智能體critic網絡有2個輸入層，由于本文采用集中學習模式，其分別用于輸入敵我雙方的狀態和動作；第2層利用Concat函數連接狀態輸入和動作輸入；第3層和第4層是激活函數為ReLu的全連接層，都包括128個隱藏節點；第5層為包含1個輸出節點的全連接層，輸出Q值。敵方智能體結構只在輸入狀態層有所不同，不再冗述。

部署策略學習算法包括兩個采用DDPG架構的智能體，分別表示敵我雙方的布局策略，這里只描述我方神經網絡結構，敵方結構與我方類似。actor網絡輸入層節點數量等于狀態維度，即為2×反潛網格分區數量（特征分別為分配矢量和重要性矢量）；第2層和第3層為全連接層，節點數量分別為16和32，其通過非線性的ReLu函數激活；第4層為Softmax層，把動作策略映射為（0，1）之間的概率值。critic網絡輸入層對應狀態輸入和動作輸入，第2層節點數量為狀態數量與動作維數量之和，即為3×反潛網格分區數量，連接狀態和動作；第3層和第4層為全連接層，節點數量分別為16和32，其通過非線性的ReLu函數激活；第5層輸出層為全連接層，節點數量為1，輸出Q值；第3層到第5層之間通過ReLu函數激活。

4.2 實驗場景及比對算法

在本文給出的實驗想定場景中，反潛海區劃分為30×30個網格分區。我方配置為：2艘護衛艦，4艘反潛UUV；敵方水下探測UUV數量為1艘（單目標）或3艘（多目標），其中護衛艦速度約為敵方UUV的3倍，我方UUV速度約為敵方UUV的1.2倍，出于數據安全考慮，這里沒有列出裝備的具體參數。另外，本文演示的實驗場景規模、敵我雙方兵力的數量不大，這主要因為隨著場景和智能體數量增加，強化學習的算力需求和訓練時間也快速增加，為了找出不同敵方目標數量和反潛海域下我方兵力的優化數量，需要通過實驗設計（design of experiment，DOE）進行大量實驗取得數據，而本文當前主要從技術思路上進行論證研究。

為了檢驗保護目標的分布情況對算法性能的影響，本文對劃分海區各個網格的設置分為兩種情況：一是各網格分區重要性指標隨機分布；另一種是規律分布，基于某真實海區的水下資源分布情況，與重要網格分區越遠，重要性越低，另外海區邊緣的重要性最低。這主要檢驗算法對不同海區的適應能力。敵方目標數量和反潛分區重要性分布是影響算法性能的兩個重要指標，為此本文采用交叉實驗，分別針對單目標隨機分布、單目標規律分布、多目標隨機分布、多目標規律分布進行了仿真實驗，在不同場景下驗證算法性能。

為了能夠檢測算法性能，本文設置了3種比對算法。因為在搜索階段，當缺少先驗知識時，如果時間充足，采用窮舉搜索；如果時間比較緊張，一般采用隨機搜索。這兩種搜索方法缺乏可比性，所以除了第3種比對算法，本文都采用第3節方法訓練好的搜索策略（部署階段為隨機分配資源），變化主要在部署方法上，說明如下：

（1）智能搜索：為本文提出的2階段反潛規劃算法，第1階段訓練的部署策略和第2階段的搜索策略，部署策略為第2階段的搜潛服務，在海區分配反潛資源。

（2）隨機部署：部署階段在反潛分區隨機分配搜潛平臺；

（3）策略梯度：采用策略梯度更新算法學習最佳反應策略，并采用經典的虛擬博弈［28-29］訓練框架使博弈雙方收斂至納什均衡；

（4）數學規劃：由于文獻［7］只考慮1個敵方探測器的情況，所以在單目標時使用該文獻提出的規劃算法。多目標時，部署階段由人工選擇資源分配方案。

4.3 仿真結果

首先在不同場景下，對本文提出的智能反潛算法與3種比對算法進行性能比較，為了能夠清楚表示演示圖形，每200個訓練輪次的樣本取一次均值，訓練曲線如圖1所示。

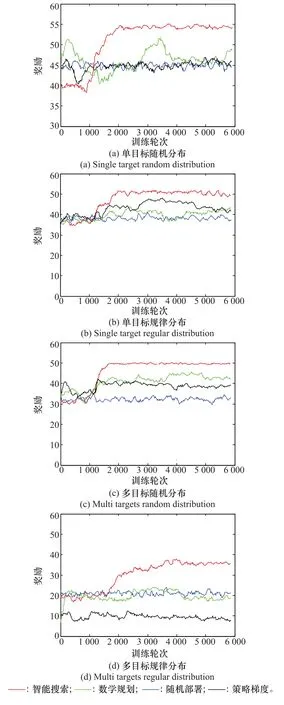
圖1 不同場景下的訓練曲線Fig.1 Training curves of different scenarios

從圖1可以看出，從收斂速度和獎勵效用性能指標方面，智能反潛算法都遠超比對算法。而且智能反潛算法的曲線變化幅度也比其他算法更小，說明其反潛策略具有更強的魯棒性。

第2個實驗檢驗算法的魯棒性。本文引入了兩個不確定參數表示反潛過程的不確定性，第1個參數為資源部署階段的敵方分布矢量l（第3.2節），表示對敵方水下探測器初始分布的不確定性，實驗時修改l的間隔范圍，即l的最大值與l的最小值之差作為調節參數；第2個不確定參數為影響探測概率的標準差（（第2節式（3））。圖2和圖3演示了場景為多目標規律分布下的實驗結果，以8 000輪訓練輪次計算得到平均獎勵值，按式（6）得到的最大后悔值作為性能指標，由于隨機部署無法處理不確定情況，所以沒有把它作為比對。圖2為不確定參數l的間隔范圍變化時針對單目標隨機分布的最大后悔值變化情況，從圖中可以看出當其他算法最大后悔值顯著增加時，智能搜索算法的增加幅度較小。

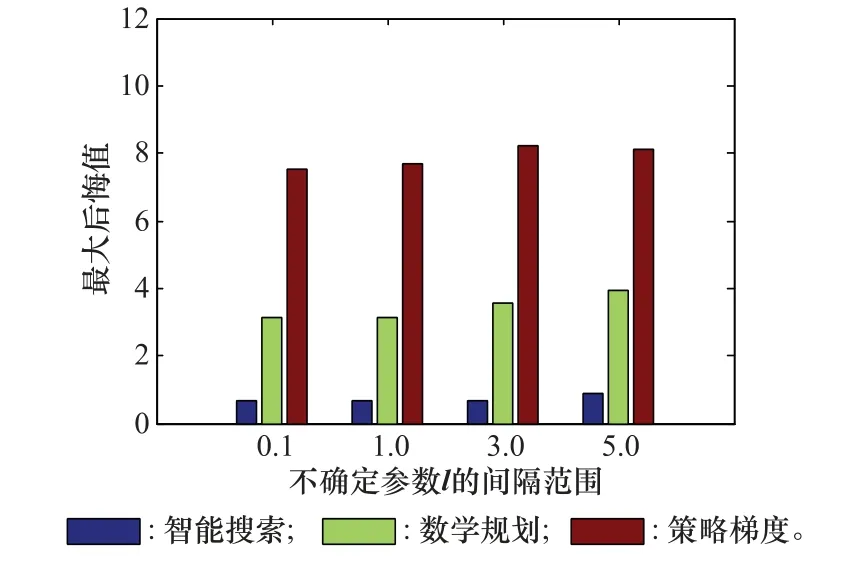
圖2 敵方分布不確定下的性能比較Fig.2 Performance of uncertain enemy distribution

圖3進一步針對不同場景和不確定參數進行了交叉實驗設計，x坐標的S［1，3］表示單目標規律分布場景下l＝1，σ＝3時不同算法的最大后悔值；M［1，3］對應多目標規律分布場景下l＝1，σ＝3時各算法的最大后悔值；其他標記與此類似，其中原數學規劃算法只支持單個目標，難以在多目標場景下對其加入不確定參數的擴展模塊，所以沒有在圖3的多目標場景下顯示。

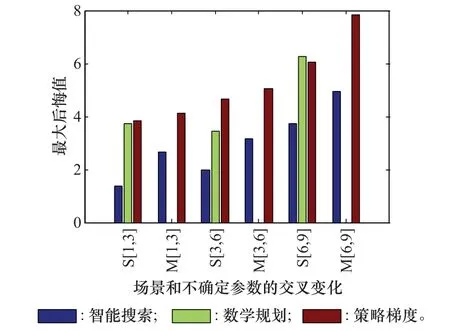
圖3 場景和不確定參數交叉變化的性能比較Fig.3 Performance comparison of cross changing of scenarios and uncertain parameters

圖4為不同場景和不確定探測概率下智能搜索算法獎勵值的變化情況，從中可以看出對應不同場景和探測概率，本算法的可擴展性能也較好。

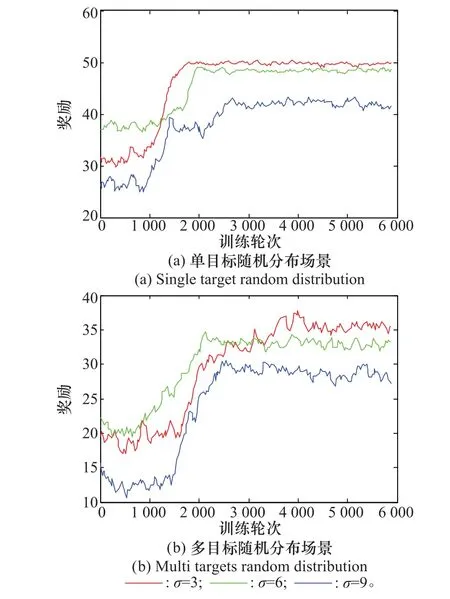
圖4 不同探測概率標準差σ下的訓練曲線Fig.4 Training curves with different detection probabilitiesσ

5 結束語

本文提出了一個基于多智能體強化學習的兩階段反潛策略學習方法，能夠在環境信息感知不確定情況下，輔助決策反潛資源的部署、巡邏、搜潛以及各資源之間的協同工作。主要優點包括：與傳統的基于數學規劃的反潛規劃方法不同的是，多智能體強化學習方法不需要事先指定敵方目標的行為模型，而是在對抗仿真中逐步增強敵我雙方的行為策略，因此本文算法不僅支持常規戰術演練，而且能生成新的反潛戰術，或者對新戰術進行性能評估。過去潛艇仿真平臺主要用于潛艇和反潛裝備性能的評估，由于缺乏戰例或想定數據，對于實戰過程中戰術推演支持不夠，而積累戰術數據需要花費大量人力物力反復推演或情報收集，而基于多智能體強化學習的策略學習算法與Alpha Zero類似，可以自我學習和生成方案。下一步工作主要集中在反潛海域以及參戰兵力規模擴大后的算法可擴展性研究。