含孔曲面自動鋪絲軌跡規劃算法
冉慶波,肖鴻,楊富鴻,段玉崗
西安交通大學 機械工程學院,西安 710049
纖維增強樹脂基復合材料(Fiber Reinforced Plastics,FRP)由于其高比強度、高比模量、可設計性強和易于整體成型等諸多優點,廣泛應用于航空航天、船舶及汽車工業的各種大型構件制造中。為實現特定功能或減少構件重量,通常需在構件表面進行開孔,例如客機機身艙門、窗口及跑車車窗等。因此在自動鋪絲軌跡規劃階段實現開孔軌跡規劃,從而可在制造階段完成開孔結構的鋪放,節約原材料,降低制造成本,縮短制造周期,具有重要意義。Hyer和Charette采用了一種通過改變纖維絲軌跡方向從而改善開孔構件力學性能的方法,雖然開孔區域應力集中有所緩解,但無法適應復雜含孔曲面。Reuschel和Mattheck以開孔圓桶作為研究對象,通過優化纖維絲軌跡降低最大主應力,充分發揮復合材料力學性能可設計的優點,但同樣無法適應復雜曲面。李俊斐等提出投影法進行開孔軌跡邊界處理,可以適應較為復雜的含孔曲面,但計算效率較低,無法適應大型復雜構件開孔操作。針對以上通過改變纖維絲軌跡鋪放方向達到開孔效果無法適應復雜曲面,以及投影法進行開孔軌跡邊界處理計算效率低下無法適應大型構件等情況,本文提出一種基于開孔邊界的軌跡規劃算法,從開孔邊界出發,在保證算法精度的前提下降低計算量,針對開孔邊界處理提出基于切線法的延長算法,從效率及精度兩個方面對算法進行驗證,最后以實際構件鋪放實驗驗證算法的正確性及合理性,算法流程圖如圖1所示。
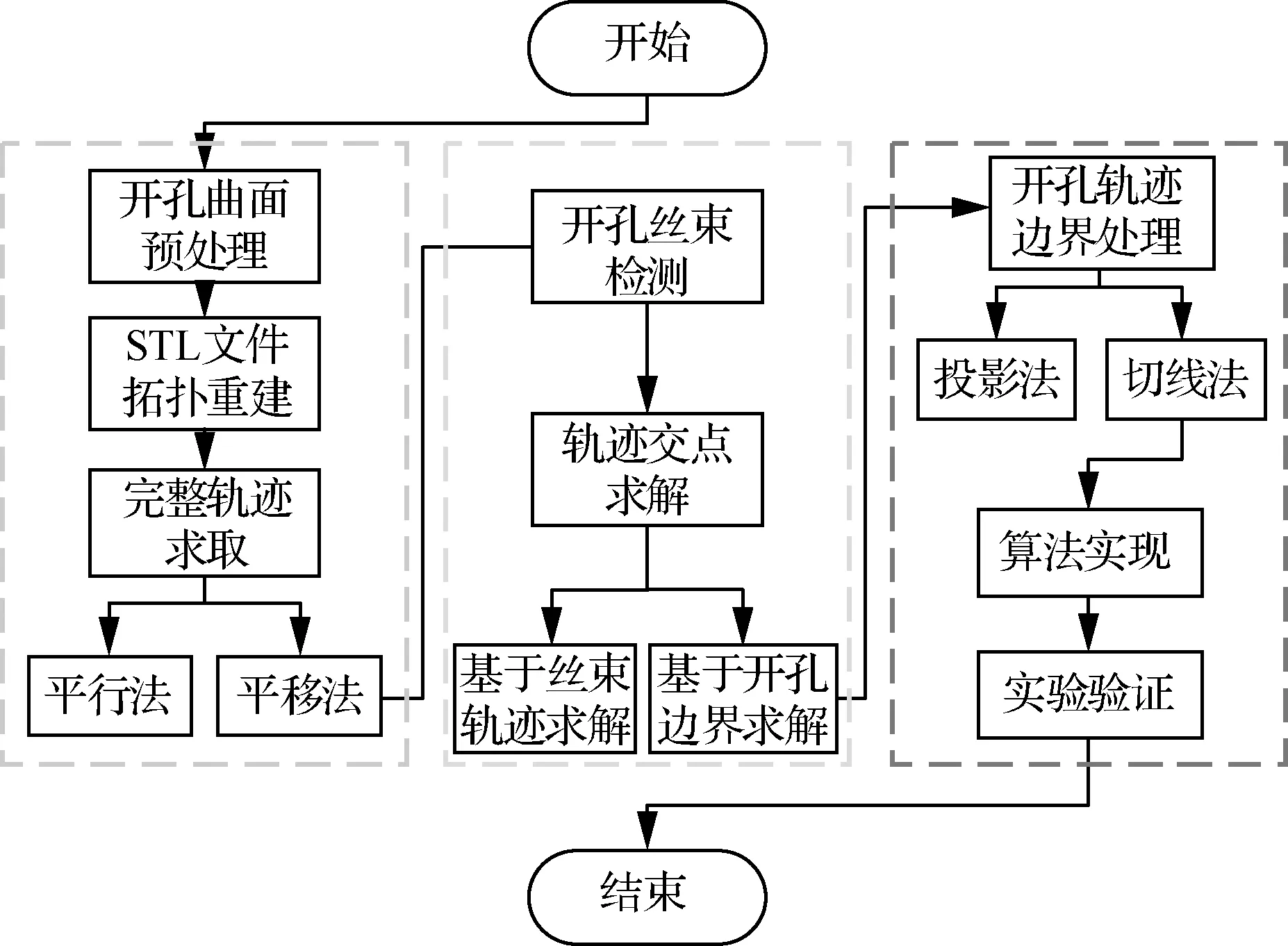
圖1 軌跡規劃整體算法流程圖Fig.1 Overall algorithm flow chart of trajectory planning
1 含孔曲面預處理
1.1 含孔曲面修復
對于軌跡規劃,要規劃的曲面必須是一個完整的曲面,否則拓撲信息不完整,無法保證生成的軌跡線在開孔兩側一一對應,除此之外其他軌跡線生成也需將之前軌跡線的相關信息用于當前軌跡線的生成及裁剪,如果之前軌跡線幾何信息不連續,則會對后續軌跡線的求解造成不便。且自動鋪絲過程需制造模具,模具或者模型表面并無開孔,而是一個完整的曲面,所以在制造模具時同樣需要完整的曲面信息。因此解決上述問題的方法就是在軌跡規劃之前對曲面沿其切線方向進行修復,目的在于既可獲取完整的曲面拓撲信息,方便后續的軌跡規劃,又可為鋪放模具的制造提供必要的數據,如圖2 所示。
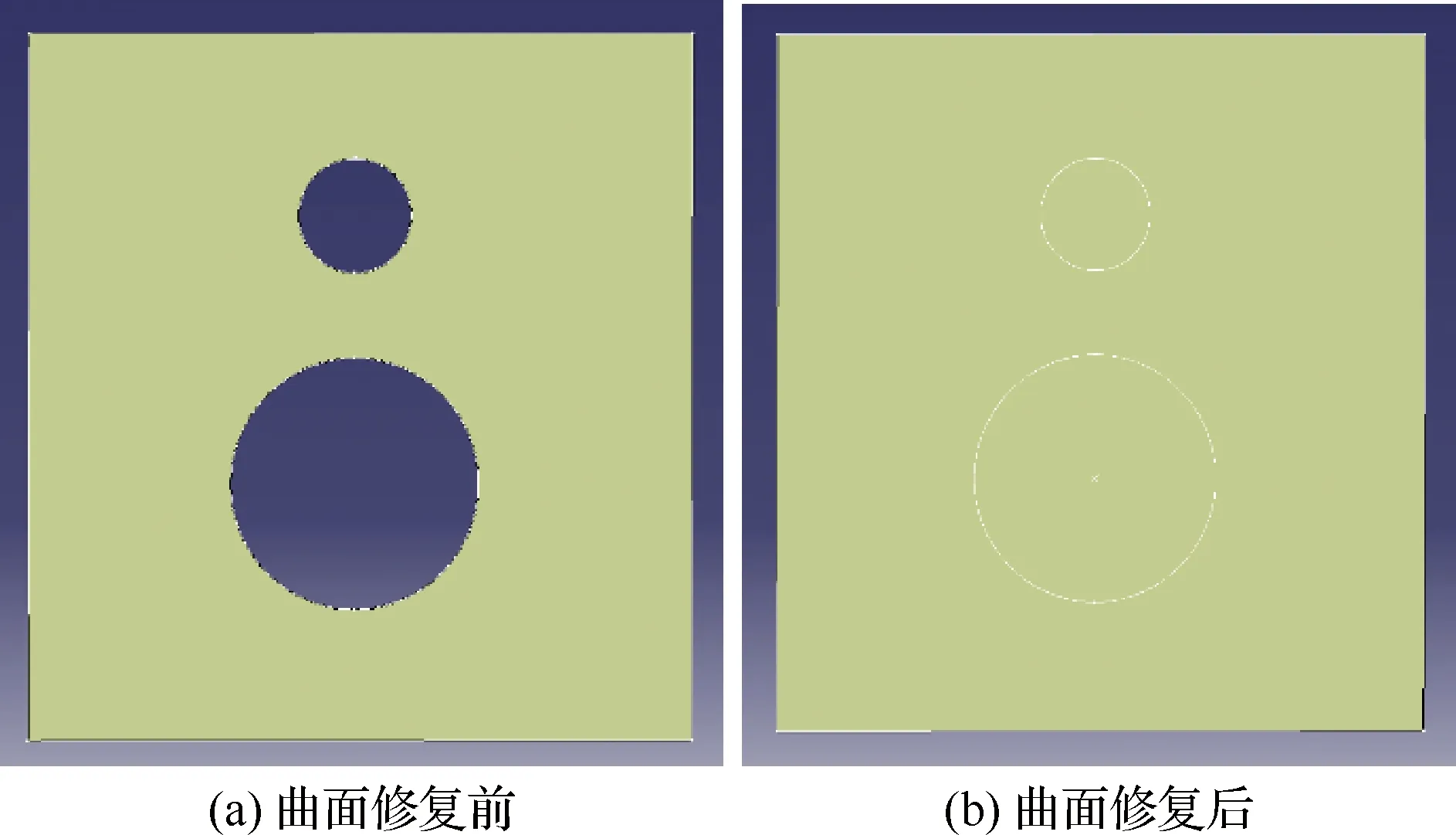
圖2 曲面預處理修復前后對比Fig.2 Comparison of surface pretreatment before and after restoration
1.2 含孔曲面STL文件拓撲重建
三角網格信息來自STL文件,其中分別記錄了三角形3個頂點的坐標值及其法向量。這種表達方式可將復雜的曲面表示成簡單的數學關系,但STL文件信息中并不包含各個三角形之間的拓撲關系,且相鄰三角形的同一個點會被重復存儲3次、4次甚至更多次,這就造成了在軌跡規劃的過程中計算數據量增大,降低了算法的效率,因此將STL文件進行拓撲重建及刪除冗余信息勢在必行,STL三角網格拓撲關系重建流程如圖3所示。
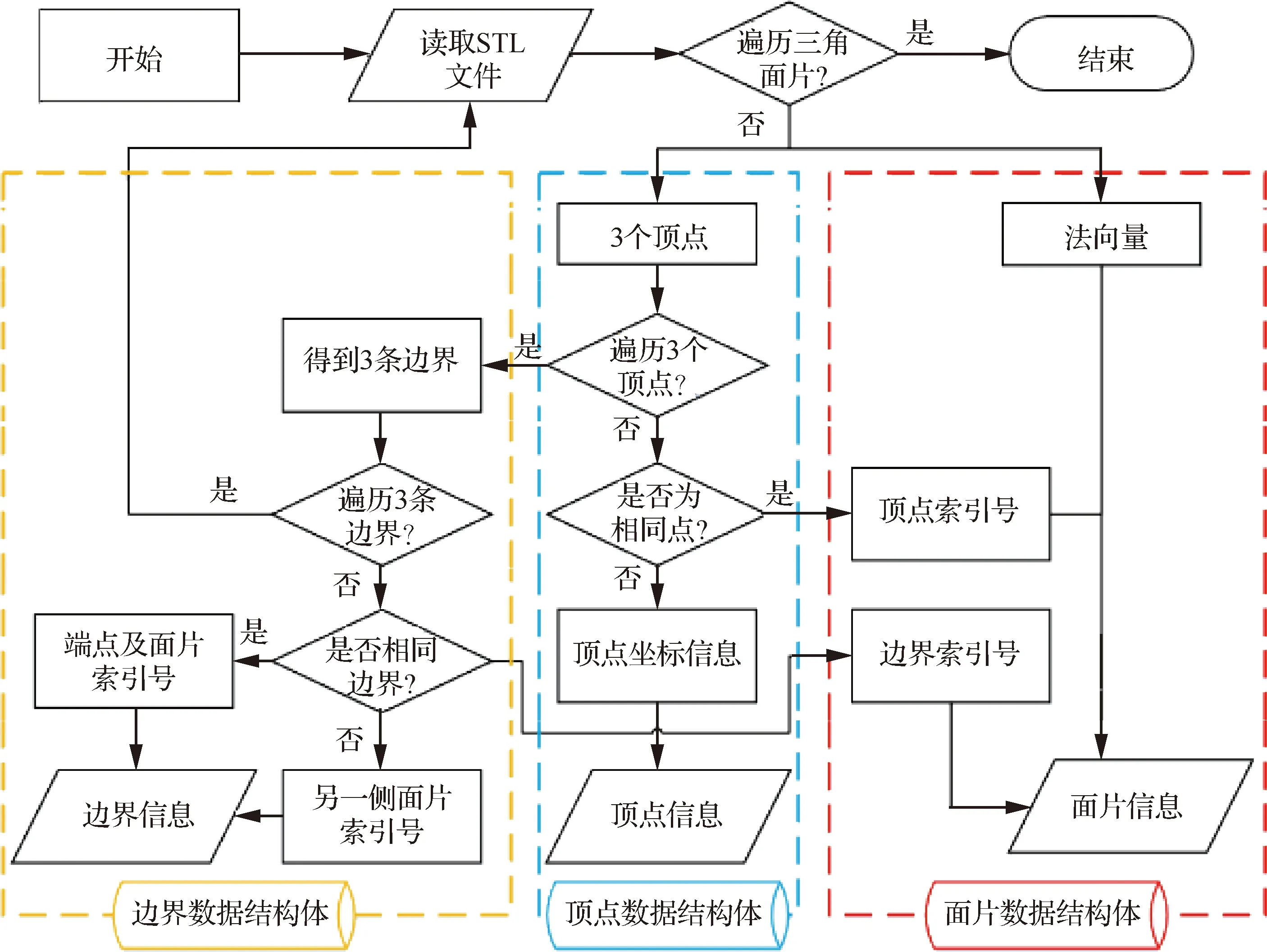
圖3 STL文件拓撲重建流程圖Fig.3 STL file topology reconstruction flow chart
針對三角面片法軌跡求解的特點,應保證建立后的拓撲關系包括頂點數據結構體、邊界數據結構體及面片數據結構體。頂點數據結構體應包含頂點編號、頂點幾何坐標值、頂點所在邊界及頂點所在三角面片的編號;邊界數據結構體應包括邊界編號、邊界頂點編號及邊界所在三角面片編號;面片數據結構體應包括面片編號、面片頂點編號、面片邊界編號及面片法向量。STL文件進行拓撲重建的目的在于去除冗余信息降低算法計算量,拓撲重建前后曲面對比如圖4所示。
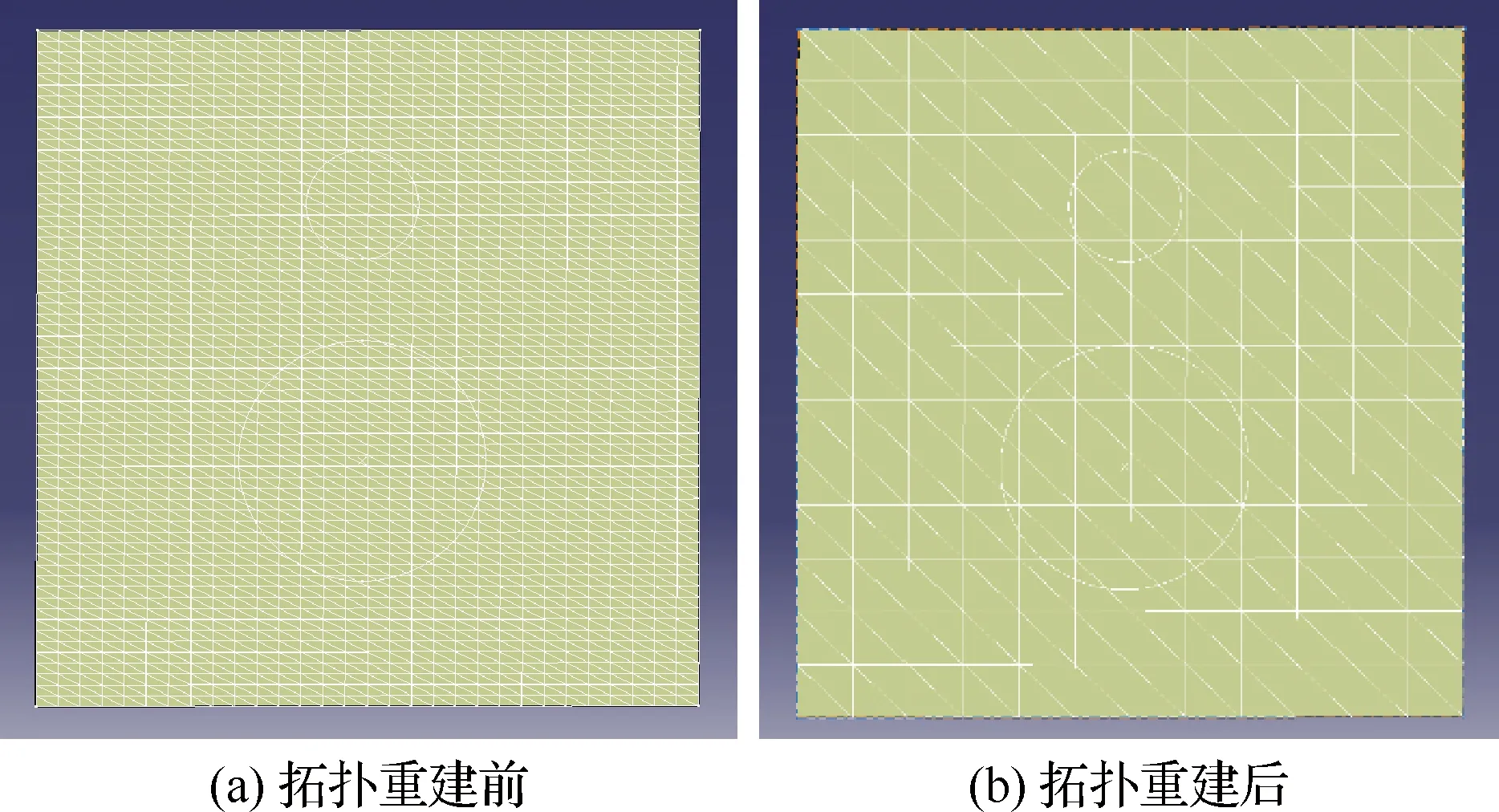
圖4 STL文件拓撲重建前后對比Fig.4 Comparison of STL files before and after topology reconstruction
2 含孔曲面軌跡規劃
2.1 完整軌跡線求取
初始纖維絲的鋪放方向選取一般有兩種構造方法:與特定初始參考線成固定角度及與設計的某一方向成固定角度。而基于初始參考軌跡生成后續纖維絲軌跡同樣有多種方法,常用的方法有平行法和平移法。平行法雖然可保證纖維絲束之間不產生間隙與重疊,但是不能保證鋪放過程中始終沿固定角度鋪放,同時也會造成折彎半徑曲率過大、纖維絲褶皺等情況,如圖5(a)所示。而平移法雖會產生斷送紗三角區,但其可保證纖維絲路徑始終沿同一角度鋪放且不產生褶皺,如圖5(b)所示。因此采用平移法進行纖維絲軌跡生成,由于軌跡生成部分并不屬于本文重點,在此不再贅述其過程。

圖5 軌跡生成方式Fig.5 Trajectory generation method
2.2 開孔絲束檢測
對于一個模型來說需開孔的區域往往只占整體模型面積的很小一部分,因此需進行開孔裁剪的纖維絲軌跡相對于整體軌跡來說也只占很小的一部分。如對所有軌跡全部進行開孔裁剪運算不僅會降低算法效率,同時也會造成算法的穩定性下降,因此提出一種開孔絲束檢測方法,以期提高算法計算效率。
首先定義開孔區域近似孔中心點,然后以一定步長遍歷開孔邊界上所有的點,,…,,計算得到近似孔中心點到開孔邊界的最遠距離:
=max[(,)]=1,2,…,
(1)
式中:(·,·)為兩點之間距離。
如圖6所示,以孔中心點為圓心,為半徑做圓,則中包含開孔區域。此時根據近似孔中心點到每條纖維絲軌跡投影距離的不同,將纖維絲路徑分為3種情況,既沒有經過開孔區域也沒有經過,沒有經過開孔區域但經過,經過開孔區域同時也經過。
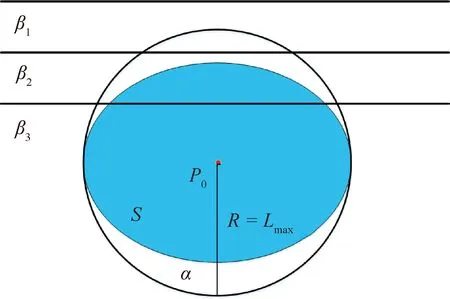
圖6 開孔絲束檢測示意圖Fig.6 Schematic diagram of opening tow detection
此時纖維絲軌跡到距離>不需進行開孔裁剪判斷,纖維絲軌跡到距離>需進行開孔裁剪判斷但判斷后不需進行裁剪,只有纖維絲軌跡到距離>需進行開孔裁剪判斷,同時需進行裁剪。針對含孔曲面零件和開孔回轉體進氣道進行實際測量,需進行裁剪操作的纖維絲軌跡分別減少了89.4%和82.5%,有效提高了算法計算效率。
2.3 開孔軌跡交點求解
根據軌跡點的遍歷方式不同,可將求解方式分為基于纖維絲軌跡的交點求解和基于孔邊界的交點求解兩種方式,對這兩種求解方式進行重點討論。
2.3.1 基于纖維絲軌跡的交點求解
在含孔曲面內,纖維絲邊界上的點與孔邊界存在著如圖7所示3種情況:情況A——點在孔邊界外部、情況B——點在孔邊界上、情況C——點在孔邊界內部。在獲取完整的纖維絲軌跡后,可根據孔邊界對軌跡進行裁剪處理,具體步驟如算法1所示

算法1 基于纖維絲軌跡的交點求解輸入: 纖維絲軌跡β,開孔邊界λ輸出: 交點所在位置前后兩點AB1: for 纖維絲軌跡上第一個點遍歷到最后一個點2: if 前后兩點全部在邊界λ外部(情況A)→不存在交點3: else if 前后兩點全部在邊界λ內部(情況C)→不存在交點4: else if 存在位于邊界λ的點→舍去該點5: else if 一點位于邊界λ外部,一點位于邊界λ內部→存在交點前后兩點6: end
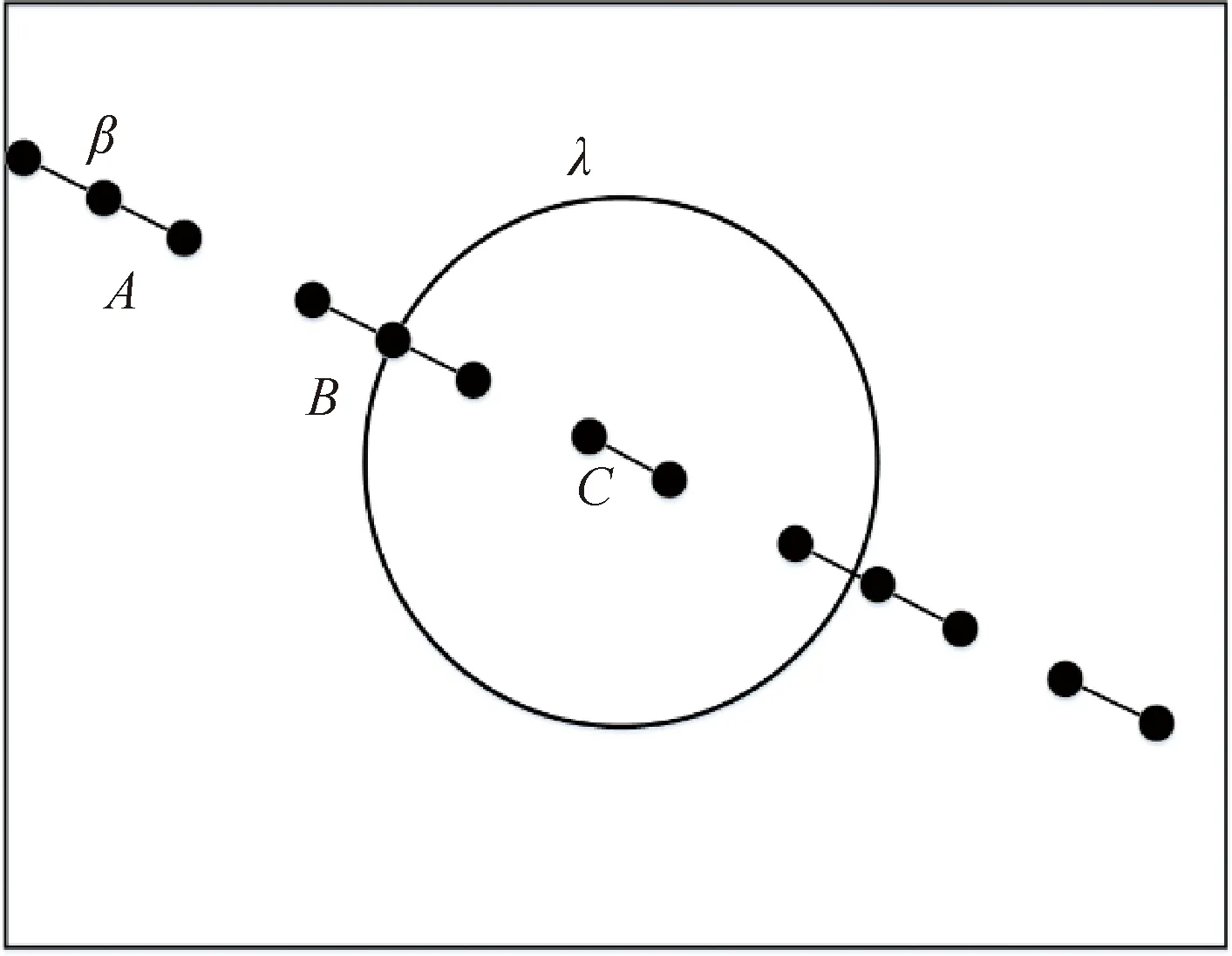
圖7 曲面開孔邊界處理示意圖Fig.7 Schematic diagram of surface opening boundary processing
算例1步驟5是求解交點的關鍵所在,因此提出利用迭代進行求解的思路。當相鄰軌跡點之間出現交點時,首先要連接兩點之間的直線,然后再求取纖維絲軌跡與孔邊界的交點。已知信息包括兩相鄰軌跡點的空間坐標信息及三角面片拓撲信息,其中拓撲信息包括兩點所在三角面片號、頂點坐標信息及相鄰三角面片信息等。基于這些信息可通過迭代的方式反復求解測地線直至找到交點。如圖8所示,求解兩點之間的交點,具體步驟見算法2。
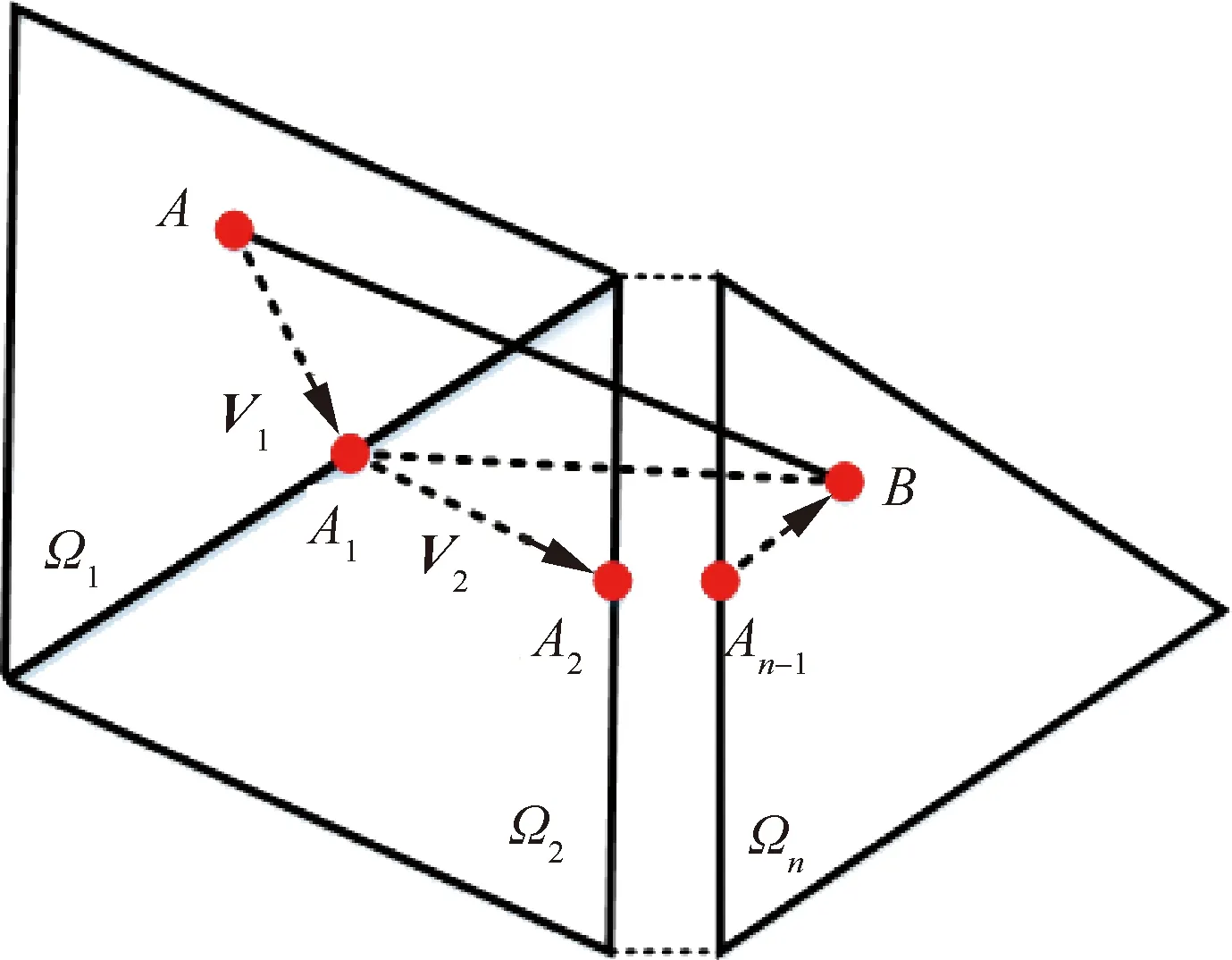
圖8 迭代求解軌跡交點示意圖Fig.8 Schematic diagram of intersection of iterative solution trajectory

由于每條纖維絲軌跡長度較長,而大多數軌跡與孔邊界只有兩個甚至一個交點,卻需迭代遍歷所有軌跡點才能判斷相鄰兩點之間的位置關系,雖保證了計算精度,但在求解交點的過程中計算量較大,降低了算法的計算效率,且隨開孔數量的增加,計算效率將進一步下降。
2.3.2 基于孔邊界的交點求解
針對基于纖維絲軌跡的交點求解算法計算效率低下的問題,提出一種基于孔邊界的交點求解算法。首先確定交點所在位置,然后精確求解交點位置,算法流程圖如圖9所示,軌跡交點求解示意圖如圖10所示,算法具體步驟見算法3。
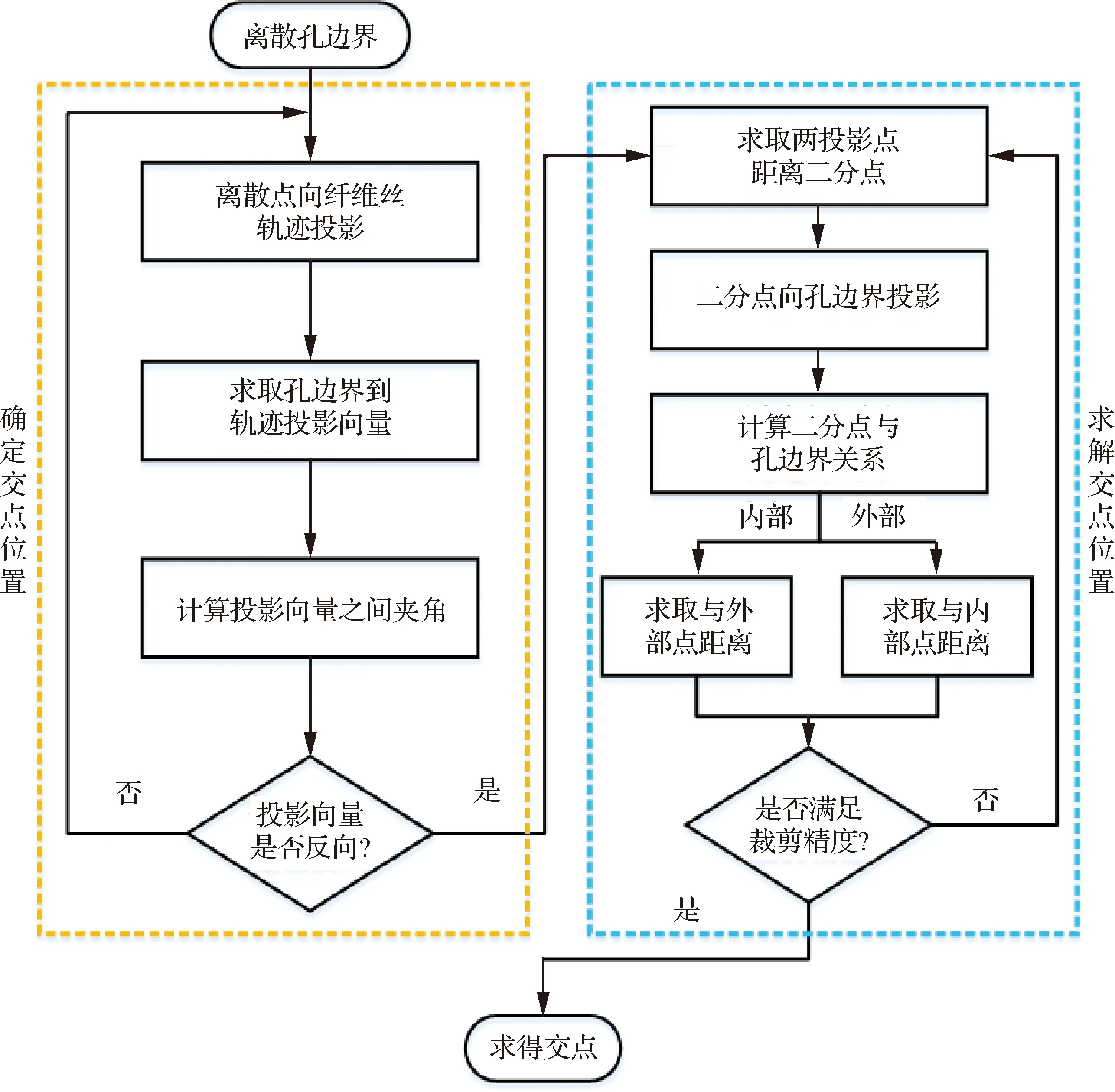
圖9 基于孔邊界求解交點算法流程圖Fig.9 Flow chart of intersection algorithm based on hole boundary
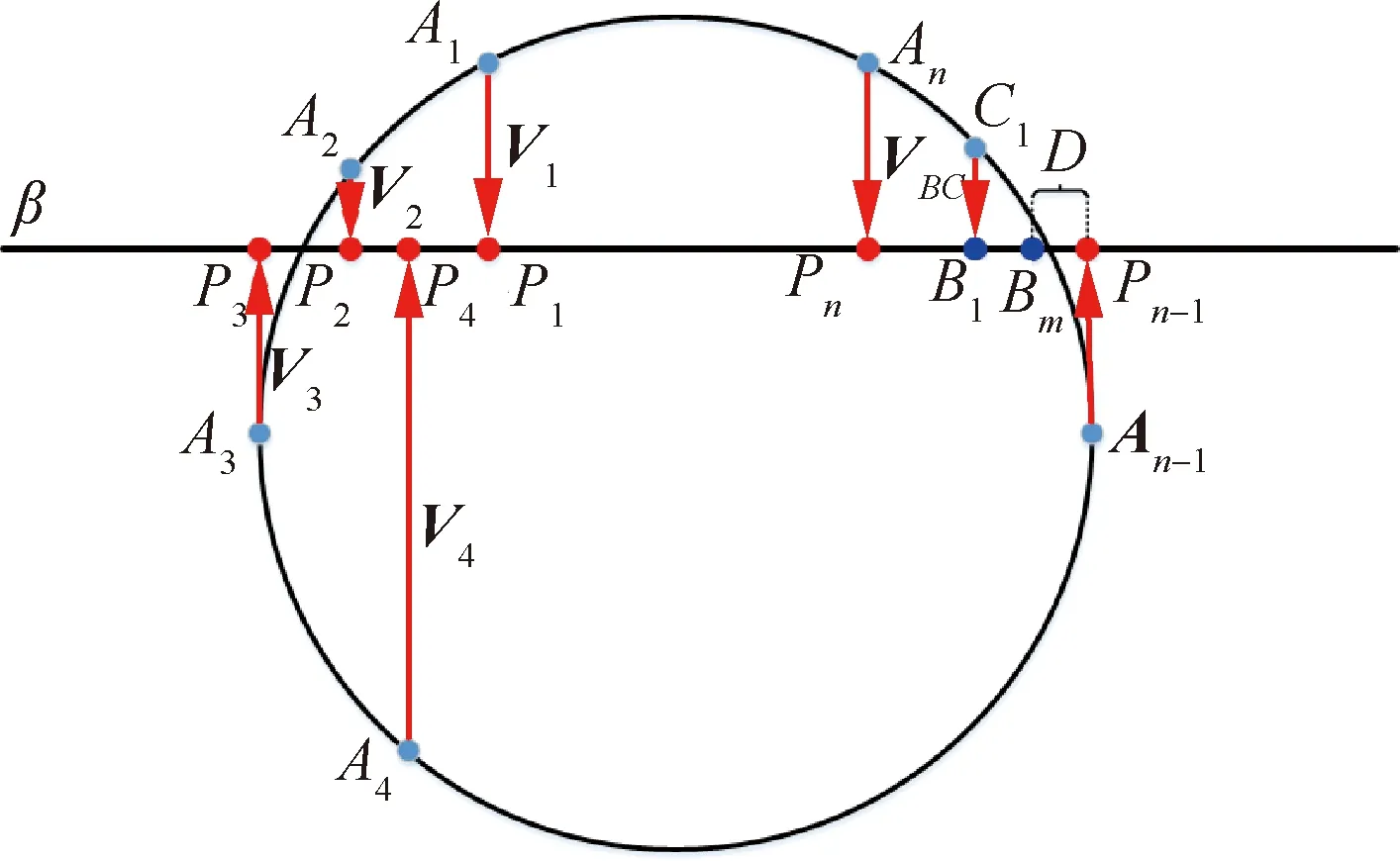
圖10 軌跡交點求解示意圖Fig.10 Schematic diagram of trajectory intersection point solution


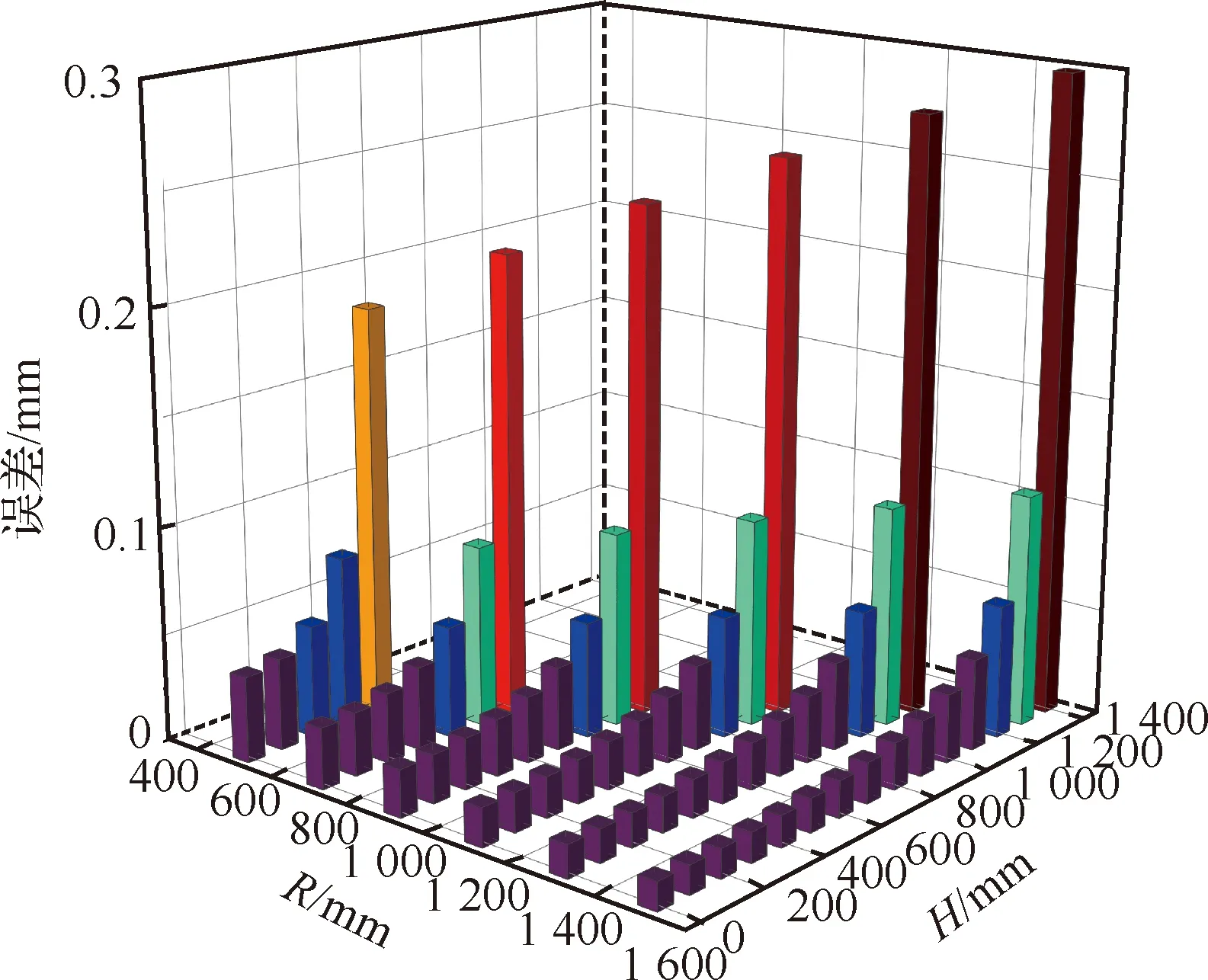
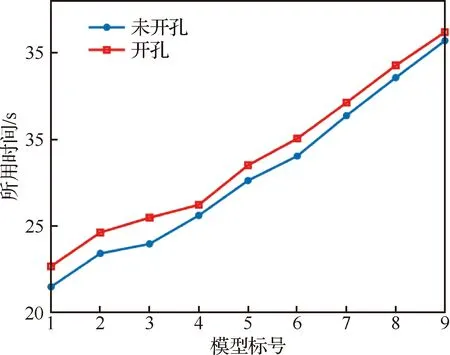
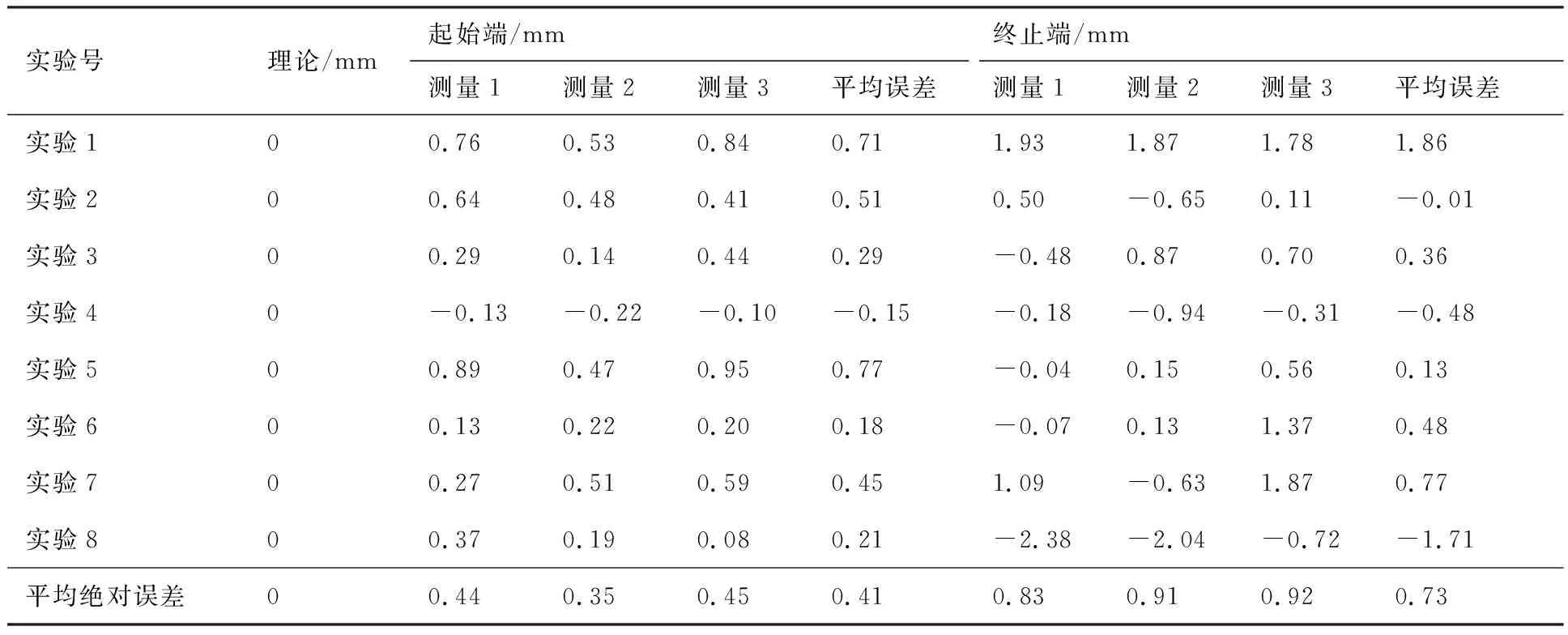
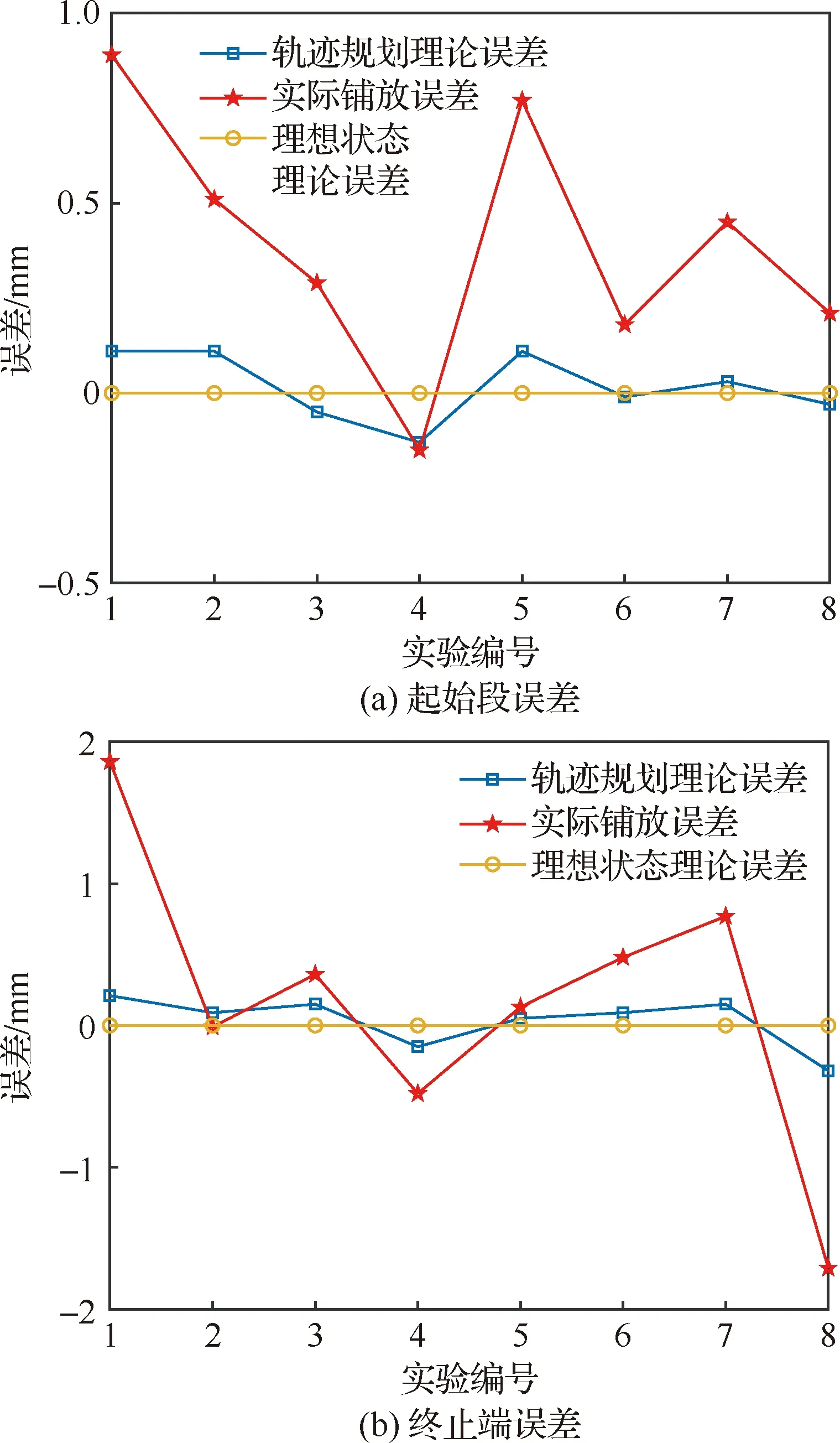
6: for 利用投影點Pn-1、Pn求出其距離二分點B17: 做B1向孔邊界最近投影點C1,得到投影向量VBC8: if 向量之間的夾角α>90°→B1處于孔邊界內部9: if交點前后兩點之間的距離D滿足D 由于含孔曲面上纖維絲的軌跡長度遠大于孔邊界的長度,且每條纖維絲軌跡都要從第一個點開始遍歷所有點,尤其當曲面尺寸變大時計算量更是成倍增長。與基于纖維絲軌跡的求解方法相比,基于開孔邊界的求解方法無需進行大量軌跡點的迭代操作,只需求解投影向量改變方向的兩點即可。除此之外,為保證交點求解精度,通過多次求解距離二分點可將誤差以指數級迅速降低,從而滿足開孔裁剪精度。因此基于孔邊界的交點求解方法雖精度上比基于纖維絲軌跡的交點求解方法有所欠缺,但其計算效率遠高于基于纖維絲軌跡的交點求解方法。當求解二分點次數足夠多時算法精度可得到保障,即采用基于孔邊界的交點求解方法在保證求解精度的同時也保證了求解過程中的計算效率。 由于纖維絲束具有寬度,而軌跡規劃一般只需規劃纖維絲束外側邊界,因此并不能簡單地以軌跡與孔邊界的交點作為斷點,如圖11所示。 圖11中紅色軌跡代表鋪絲設備運動主軌跡,不進行裁剪。對于上半圓,主軌跡上側纖維絲軌跡如果以交點為斷點,則可完全覆蓋含孔曲面,主軌跡下側纖維絲軌跡如果交點為軌跡斷點,則會形成空白三角區。但對于下半圓則相反,主軌跡下側纖維絲軌跡以交點為斷點,則可完全覆蓋含孔曲面,主軌跡上側纖維絲軌跡以交點為軌跡斷點,則會形成空白三角區。三角區的存在會造成構件開孔區域力學性能下降,因此纖維絲軌跡需延長,確保其能完整覆蓋曲面。針對軌跡邊界延長提出投影法和切線法兩種延長算法。 圖11 軌跡規劃邊界三角區Fig.11 Triangle area of trajectory planning boundary 2.4.1 投影法 由圖11可發現對于上半圓,空白區域的長度是上一條纖維絲軌跡與孔邊界的交點和當前纖維絲軌跡與孔邊界交點在纖維絲軌跡方向的長度,對于下半圓,結論同樣適用,只不過此時變成主軌跡上側纖維絲軌跡需延長。因此提出一種投影法計算延長距離,具體步驟見算法4。 算法4 投影法求解延長點輸入: 兩條纖維絲軌跡β4、β5輸出: 是否需要延長及延長距離δ1: β4與孔邊界的交點P4向β5進行投影,得到投影點P52: if投影點P5屬于孔邊界內部(通過2.3.2節中的算法進行判斷)3: →不需要延長4: else →需要延長,且延長距離δ5: end 雖投影法精度可得到保證,但多次投影求解也會降低算法計算效率。 2.4.2 切線法 針對投影法投影運算降低計算效率的問題提出切線法,避免投影法的缺陷。如圖12所示,主要是求解延長距離,具體步驟見算法5。 對于圓的上半部分,如圖12所示,左上側主軌跡下側纖維絲軌跡向量之間的夾角、小于90°,需要延長,上側不需要延長。而對于圓的下半部分,如圖12所示,下半圓的主軌跡下側纖維絲軌跡向量夾角大于90°,不需延長,因此切線法對于整圓全部都是適用的。對于開孔邊界是直線的情況,如圖12右上側直線開孔邊界所示,由于纖維絲軌跡與孔邊界的交點做出孔邊界的切線向量與孔邊界方向一致,因此無論是投影法還是切線法求得的延長距離相同,不存在誤差。而對于開孔邊界是曲線的情況,如圖12左上側曲線開孔邊界所示,由于纖維絲軌跡與孔邊界的交點做出孔邊界的切線向量與孔邊界方向并不一致,因此投影法與切線法求得的延長距離并不相同,存在誤差。由于開孔邊界曲線并沒有一般規律,因此誤差也沒有特定計算公式,但是在很小的范圍內(纖維絲束寬度一般為6.35 mm)可近似認為開孔邊界曲線是一段圓弧,因此可得出誤差計算公式。 圖12 切線法求解延長距離Fig.12 Tangent method for solving extended distance 如圖13所示,為開孔區域圓心,則切線向量與纖維絲軌跡方向向量之間的偏轉角的計算公式為 (5) 切線法延長距離計算公式為 (6) 投影法延長距離計算公式為 (7) 因此可計算出切線法與投影法之間的誤差為 (8) 圖13 切線法求解延長距離誤差計算Fig.13 Calculation of error of extended distance by tangent method 從式(8)中可分析出誤差的大小只與開孔區域半徑和纖維絲束所在高度有關。 從圖14中可發現,在高度一定的情況下,隨開孔半徑的不斷增大,誤差不斷減小;在開孔半徑一定的情況下,隨高度增大,誤差也隨之增大,但兩者的誤差都在纖維絲自動鋪放允許的精度之內,因此算法可保證開孔邊界精度。 圖14 切線法求解延長距離相對誤差Fig.14 Tangent method for solving relative error of extended distance 纖維絲自動鋪放過程涉及多方面內容,信息復雜,計算量大,且需保證獲得的鋪放信息準確無誤,搭建自動鋪絲CAD/CAM軟件系統是實現復合材料自動化快速成型的重要保證。在第2節設計算法的基礎上搭建軟件開發平臺,為提高算法的通用性及兼容性,選取在航空航天領域通用的CAD/CAM平臺CATIA作為軟件開發平臺,基于Visual Studio 2005軟件,采用CATIA V5 Component Application Architecture (CATIA V5 CAA)技術實現算法。 為檢驗所提軌跡規劃算法,特別是鋪放路徑在開孔處的軌跡規劃情況,分別以開孔平板及開孔回轉體進行算法驗證。以絲束數量為8、絲束寬度為6.35 mm進行軌跡規劃,開孔平板及開孔回轉體軌跡規劃效果如圖15所示。 圖15 開孔構件軌跡規劃效果Fig.15 Trajectory planning effect of perforated components 為進一步驗證開孔軌跡規劃效果及精度,利用課題組自主研發的8絲束鋪絲頭,集成重送、剪切、夾持、加熱、壓緊等模塊,對開孔平板、開孔回轉體進行實際鋪放,鋪放材料為美國赫氏公司HexPlyM21碳纖維,標稱帶寬為(6.350±0.125) mm,鋪放實驗時室溫為23 ℃,加熱溫度為35 ℃,鋪放速度為150 mm/s,鋪放壓力為500 N。 開孔構件實際鋪放效果如圖16所示。從軌跡規劃及實際鋪放效果看,各絲束均能準確到達邊界且自動判斷是否延長及延長距離,因此提出的基于開孔邊界的軌跡規劃算法能高效地對開孔構件進行軌跡規劃,且符合實際工程需求。 開孔軌跡規劃算法的規劃效率指的是該算法鋪放完成一個具體模型所需的時間,為驗證提出的開孔規劃算法的效率,按曲面復雜程度及曲面鋪放面積由小到大選取了9個模型,分別計算其開孔與未開孔情況下規劃完成整個曲面所需的時間,結果如圖17所示。 從圖17中可看出隨模型復雜程度增加及鋪放面積增大,規劃軌跡所需時間也隨之增加,另外開孔與否對整個曲面軌跡規劃所需時間影響并不大,平均時間增加3.41%,并沒有明顯降低整體算法效率,且隨模型復雜程度增加及鋪放面積增大,開孔與未開孔軌跡規劃之間的時間差越來越小,這是由于絲束程度對基于開孔邊界的軌跡規劃算法并沒有影響,隨曲面增大,開孔所需時間占總體規劃時間越來越少,進一步證明了所提基于開孔邊界的軌跡規劃算法的優越性。 圖17 軌跡規劃效率對比Fig.17 Comparison of trajectory planning efficiency 軌跡的邊界精度是指鋪放成型絲束的邊界與設定邊界的差異,其中纖維絲束邊界包含起始邊界和結束邊界,在軌跡中分別通過重送指令和剪切指令進行控制。邊界誤差是一個綜合誤差,包含絲束重送長度和剪切長度的測量誤差、機器人的定位誤差、在軌跡規劃階段算法設置的邊界覆蓋策略誤差及邊界裁剪精度。為驗證提出的開孔邊界裁剪算法的準確性,將以平板標準測定模具的0°軌跡100%覆蓋為例進行規劃測試,驗證算法邊界精度。 3.3.1 軌跡規劃理論邊界精度驗證 對軌跡規劃理論邊界精度進行測量,驗證軌跡規劃邊界精度。軌跡規劃絲束效果及邊界精度誤差如圖18所示。標稱帶寬6.35 mm作為軌跡規劃標準帶寬,0°軌跡100%覆蓋策略的測量實驗數據如表1所示。 圖18 軌跡規劃理論邊界誤差示意圖Fig.18 Schematic diagram of theoretical boundary error of trajectory planning 表1 100%覆蓋策略軌跡規劃理論邊界誤差 對于實際的軌跡規劃,過高的精度對最后的鋪放效果并沒有實際意義,只會引起計算機求解迭代次數過多,造成計算機資源浪費。通過表1軌跡規劃邊界延長精度實驗數據可看出,對于提出的開孔軌跡規劃算法,軌跡規劃纖維絲束的理論邊界控制精度平均絕對誤差為0.11 mm,滿足航空航天鋪絲工藝邊界精度要求。 3.3.2 實際鋪放邊界精度驗證 為測量實際邊界精度,驗證邊界控制精度,對100%覆蓋策略的0°軌跡進行實際鋪放,鋪放絲束效果及邊界測量示意圖如圖19所示。同時實驗前在平板模具上先行測量設備的重送距離和剪切距離,經實驗鋪放測量量設定重送距離為97 mm,剪切距離為98 mm。 圖19 實際鋪放邊界及局部放大測量Fig.19 Actual laying boundary and local enlarged survey 取美國赫氏公司HexPlyM21碳纖維的標稱帶寬為6.35 mm,100%覆蓋策略的測量實驗數據如表2所示,可知對于提出的開孔軌跡規劃算法,纖維絲束的實際鋪放邊界控制精度平均絕對誤差為0.57 mm,滿足航天航空鋪絲工藝邊界精度要求。 表2 100%覆蓋策略實際鋪放誤差 3.3.3 誤差分析 為更加清晰地分析提出的開孔軌跡規劃算法誤差來源,將起始端和終止端3種誤差統一分析。 從圖20中可看出理想狀態的軌跡規劃理論誤差一直是0,而軌跡規劃理論誤差由于計算機資源及算法計算效率的限制,不可能無限制地逼近理論誤差,因此只需滿足誤差在一定可接受的范圍內即可。對實際鋪放來說,由于實際鋪放誤差是一個綜合誤差,不僅包含在軌跡規劃階段算法設置的邊界覆蓋策略誤差、邊界裁剪精度,還包含絲束重送長度和剪切長度的測量誤差、機器人的定位誤差。因此實際鋪放誤差大于軌跡規劃理論誤差,但與軌跡規劃理論誤差變化趨勢相同。 圖20 軌跡誤差分析Fig.20 Trajectory error analysis 針對大型復雜開孔構件軌跡規劃,主要對以下內容進行了研究: 1) 研究了纖維絲軌跡生成方式,提出修復含孔曲面不僅可獲取完整的曲面拓撲信息,方便后續的軌跡規劃,又可為鋪放模具的制造提供必要數據。對修復完成的曲面通過STL文件提出三角網格信息,并重建網格之間的拓撲信息。通過纖維絲軌跡與近似孔中心點的幾何關系確定需要裁剪的纖維絲軌跡,降低算法計算量。 2) 針對開孔邊界交點問題提出基于纖維絲軌跡的交點求解及基于孔邊界的交點求解兩種算法,通過對兩種算法的優劣勢對比,最終決定采用基于孔邊界的交點求解算法,此算法在滿足精度要求的前提下可大幅度提升算法效率。 3) 針對纖維絲軌跡孔邊界處理問題提出投影法和切線法兩種延長算法,通過研究發現兩種算法都可滿足邊界裁剪精度要求,但相比于投影法,切線法計算量更小,算法效率更高,因此采用切線法進行開孔邊界處理。 4) 對CATIA軟件進行二次開發,基于Visual Studio 2005軟件平臺采用CATIA V5 CAA技術實現算法,并針對不同構件進行算法驗證,對開孔平板及開孔回轉體進行實際鋪放實驗,證明了算法的正確性且驗證了其符合實際工程需求。對不同曲面復雜程度及曲面鋪放面積的9個模型進行軌跡規劃,結果顯示開孔與否對整個曲面軌跡規劃所需時間影響并不大,平均時間增加3.41%,開孔并沒有明顯降低整體算法效率。通過對平板標準測定模具的0°軌跡100%覆蓋算例進行規劃測試,驗證了軌跡規劃邊界精度平均絕對誤差為0.11 mm,實際鋪放邊界精度平均絕對誤差為0.57 mm,最終對誤差進行分析,滿足航天航空鋪絲工藝邊界精度要求。2.4 開孔軌跡邊界處理


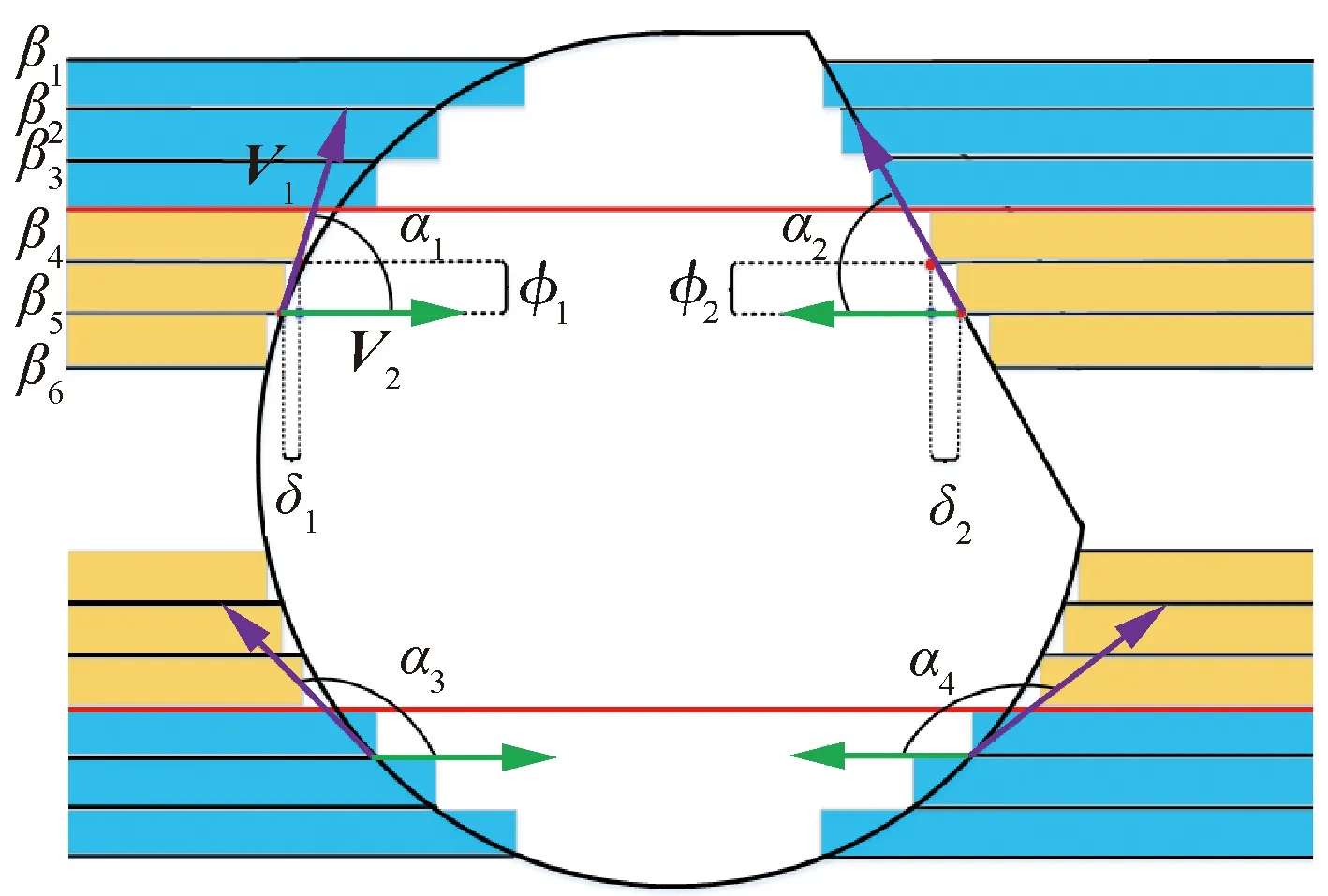


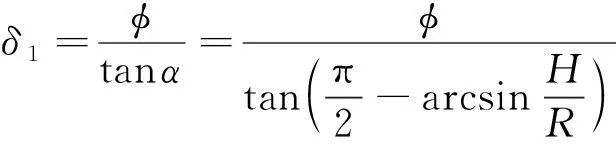
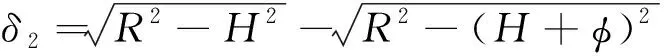
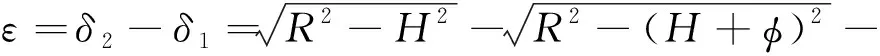
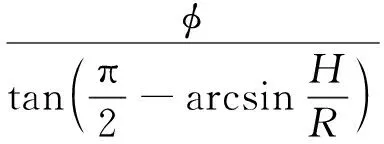

3 算法實現與實驗驗證
3.1 開孔軌跡規劃算法鋪放驗證
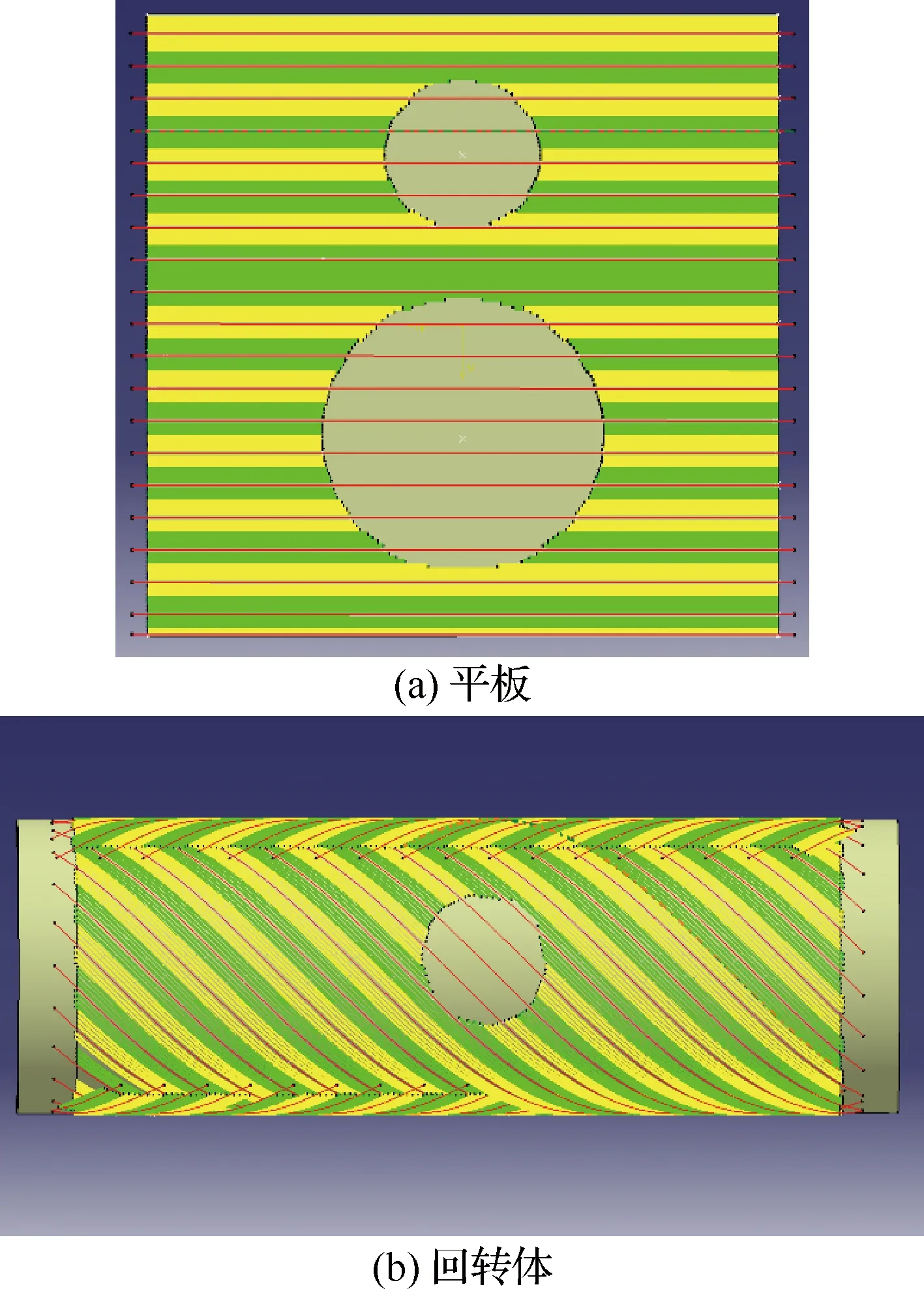

3.2 開孔軌跡規劃算法效率驗證
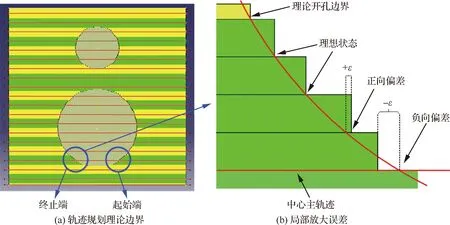
3.3 開孔軌跡規劃算法精度驗證


4 結 論

